전체 글
-
★모평균 차의 구간추정★기초통계학-[대표본 추정 -05]2023.01.11
-
★모비율의 신뢰구간★기초통계학-[대표본 추정 -04]2023.01.11
-
★신뢰구간★신뢰도★구간추정★기초통계학-[대표본 추정 -03]2023.01.11
-
★표본비율차이에 따른 표준정규분포★기초통계학-[연습문제02 -21]2023.01.11
★모평균 차의 구간추정★기초통계학-[대표본 추정 -05]
1. 모평균 차의 구간 추정
https://knowallworld.tistory.com/307
★두 표본평균의 차에 대한 표본분포(모분산 알때 , 동일할때)★중심극한정리 활용★이표본의
1. 이표본의 표본분포 ==>지금까지는 단일 모집단의 표본에 대한 통계량의 표본분포 EX) 수능에서 남학생, 여학생 집단의 평균이 동일한지 여부 비교 ==> 비교위해서는 각각 표본을 추출하여야 한
knowallworld.tistory.com
==> 모평균 차의 구간 추정


==> 두 모평균의 차에 대한 점추정량 |X - |Y
==>모평균간 차에 대한 90% 신뢰구간
print(z_1)
#%%
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 90#신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(-5.5 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\left( \overline{x}-\overline{y}\right)$' +f'-{z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$' +' , '+ r'$\left( \overline{x}-\overline{y}\right)$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$',fontsize=15)
==>모평균간 차에 대한 95% 신뢰구간
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95#신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(-5.5 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\left( \overline{x}-\overline{y}\right)$' +f'-{z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$' +' , '+ r'$\left( \overline{x}-\overline{y}\right)$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$',fontsize=15)
==>모평균간 차에 대한 99% 신뢰구간
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 99#신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(-5.5 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\left( \overline{x}-\overline{y}\right)$' +f'-{z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$' +' , '+ r'$\left( \overline{x}-\overline{y}\right)$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$',fontsize=15)
EX-01) 대도시와 중소도시의 무연 휘발유 가격에 차이가 있는지 알아보기 위하여 표본조사한 결과, 다음과 같은 자료를 얻었다. 이때 두 지역 간 간격 차이의 평균에 대한 95% 신뢰구간을 구하라.(모표준편차가 각각 80원과 30원인 정규분포를 따른다. 단위는 1000원이다.)
A = [1.69, 1.79, 1.68, 1.72, 1.66, 1.73, 1.59, 1.78, 1.72, 1.63, 1.55, 1.85]
B = [1.46, 1.47, 1.42, 1.51, 1.55, 1.52, 1.48, 1.47, 1.53, 1.5]
A의 평균 : 1.699
B의 평균 : 1.49
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95#신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(-5.5 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\left( \overline{x}-\overline{y}\right)$' +f'-{z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$' +' , '+ r'$\left( \overline{x}-\overline{y}\right)$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$',fontsize=15)
A = '1.69 1.79 1.68 1.72 1.66 1.73 1.59 1.78 1.72 1.63 1.55 1.85'
B = '1.46 1.47 1.42 1.51 1.55 1.52 1.48 1.47 1.53 1.50'
A = list(map(float , A.split(' ')))
B = list(map(float , B.split(' ')))
MEANS_A = np.mean(A)
MEANS_B = np.mean(B)
Var_A = 0.08**2
Var_B = 0.03**2
ax.text(2 , .25, f'모평균의 차에 대한 신뢰구간 {trust}% : \n' + f'{round((MEANS_A-MEANS_B) - (z_1)*math.sqrt(Var_A/len(A) + Var_B/len(B)),3)} ~ {round((MEANS_A-MEANS_B) + (z_1)*math.sqrt(Var_A/len(A) + Var_B/len(B)),3)}' , fontsize= 15)
EX-02) 모표준편차가 동일하게 80원이라 할때 , 두 지역 간 가격 차이의 평균에 대한 90% 신뢰구간을 구하라.
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 90#신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(-5.5 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\left( \overline{x}-\overline{y}\right)$' +f'-{z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$' +' , '+ r'$\left( \overline{x}-\overline{y}\right)$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$',fontsize=15)
A = '1.69 1.79 1.68 1.72 1.66 1.73 1.59 1.78 1.72 1.63 1.55 1.85'
B = '1.46 1.47 1.42 1.51 1.55 1.52 1.48 1.47 1.53 1.50'
A = list(map(float , A.split(' ')))
B = list(map(float , B.split(' ')))
MEANS_A = np.mean(A)
MEANS_B = np.mean(B)
Var_A = 0.08**2
Var_B = 0.08**2
ax.text(2 , .25, f'모평균의 차에 대한 신뢰구간 {trust}% : \n' + f'{round((MEANS_A-MEANS_B) - (z_1)*math.sqrt(Var_A/len(A) + Var_B/len(B)),3)} ~ {round((MEANS_A-MEANS_B) + (z_1)*math.sqrt(Var_A/len(A) + Var_B/len(B)),3)}' , fontsize= 15)

출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 대표본 추정' 카테고리의 다른 글
| ★모평균의 차에 대한 신뢰구간★모비율에 대한 표본크기 구하기★표본의 크기★기초통계학-[대표본 추정 -06] (0) | 2023.01.12 |
|---|---|
| ★string r'로 받을때 안에 값 집어넣기(변수로도 %2d)★모비율 차의 구간추정★기초통계학-[대표본 추정 -06] (0) | 2023.01.11 |
| ★모비율의 신뢰구간★기초통계학-[대표본 추정 -04] (0) | 2023.01.11 |
| ★신뢰구간★신뢰도★구간추정★기초통계학-[대표본 추정 -03] (0) | 2023.01.11 |
| ★불편추정량★최소분산불편추정량★유효 추정량★불편 추정량★기초통계학-[대표본 추정 -02] (0) | 2023.01.11 |
★모비율의 신뢰구간★기초통계학-[대표본 추정 -04]
1. 모비율의 신뢰구간
https://knowallworld.tistory.com/306
이항분포에 따른 정규분포의 표준정규분포화★표본비율의 표본분포★기초통계학-[모집단 분포
1.표본비율의 표본분포 EX) 이항 확률변수의 실질적인 응용 ==> 여론조사 생각 ==> 모집단을 구성하는 사람들의 어느 특정 사건을 선호하는 비율(p)를 알기 위하여 n명으로 구성된 표본을 임의 선정
knowallworld.tistory.com
https://knowallworld.tistory.com/319
★표본비율의 표본분포에 대한 정규분포 근사★표본비율★N(모평균 , 모평균*(1-모평균) / 전체표
20. 모비율이 p= 0.25인 모집단으로부터 크기가 각각 다음과 같은 표본을 임의로 선정한다. 표본비율이 p+-1 0.1 안에 있을 근사확률을 구하고, 표본의 크기가 커짐에 따른 확률의 변화를 비교 https://
knowallworld.tistory.com
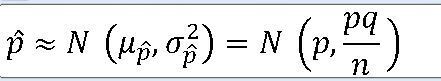
==> 표본의 크기가 클수록 표본비율 ^p는 모비율 p에 근접한다.
==> 모비율에 대한 90% 신뢰구간
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 90 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\widehat{p}$' +f'-{z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$' +' , '+ r'$\widehat{p}$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$',fontsize=15)
==> 모비율에 대한 95% 신뢰구간
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\widehat{p}$' +f'-{z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$' +' , '+ r'$\widehat{p}$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$',fontsize=15)
==> 모비율에 대한 99% 신뢰구간
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 99 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\widehat{p}$' +f'-{z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$' +' , '+ r'$\widehat{p}$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$',fontsize=15)
EX-01) 부산에서 4년 이상 거주하고 있는 외국인 110명을 상대로 한국 문화에 대한 인지 수준을 조사한 결과 한국 문화를 알고 있다고 응답한 비율이 88.2%이다. 우리나라에서 4년 이상 거주하고 있는 외국인의 한국 문화에 대한 인지 비율에 대한 95% 신뢰구간을 구하라.
^p = 0.882
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\widehat{p}$' +f'-{z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$' +' , '+ r'$\widehat{p}$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$',fontsize=15)
#\widehat{p}-\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}
# ex = '93.242 89.635 92.660 92.540 94.883 102.165 93.326 90.880 93.684 91.564 88.727 94.317 88.166 96.085 82.028 97.213 99.338 93.381 86.498 83.348 97.262 89.656 84.045 89.113 81.562 87.180 94.345 92.436 93.633 97.276'
# A = list(map(float, ex.split(' ')))
# print(A)
RATIO = 0.882
n = 110
# print((z_1 * STDS / math.sqrt(len(A))))
ax.text(2 , .25, f'신뢰구간 모비율에 대한 {trust}% : \n' + f'{round(RATIO - z_1*math.sqrt(RATIO * (1-RATIO) / n) ,3)} ~ {round(RATIO + z_1*math.sqrt(RATIO * (1-RATIO) / n),3)}' , fontsize= 15)
ax.text(2 , .35, r'$\sqrt{\widehat{p}\widehat{q}} = $' + f'{round(math.sqrt(RATIO * (1-RATIO)),3)}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(n),2)}',fontsize=15)
print(z_1)
EX-02) 부산에서 외국인 800명을 상대로 한국의 의료환경에 대한 만족도를 조사한 결과 38.5%가 만족한다고 응답, 이자료를 기초로 한국에 거주하는 외국인이 우리나라 의료환경에 만족하는 비율에 대한 95% 신뢰구간을 구하라.
^p = 0.385
n = 800
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\widehat{p}$' +f'-{z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$' +' , '+ r'$\widehat{p}$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$',fontsize=15)
RATIO = 0.385
n = 800
# print((z_1 * STDS / math.sqrt(len(A))))
ax.text(2 , .25, f'신뢰구간 모비율에 대한 {trust}% : \n' + f'{round(RATIO - z_1*math.sqrt(RATIO * (1-RATIO) / n) ,3)} ~ {round(RATIO + z_1*math.sqrt(RATIO * (1-RATIO) / n),3)}' , fontsize= 15)
ax.text(2 , .35, r'$\sqrt{\widehat{p}\widehat{q}} = $' + f'{round(math.sqrt(RATIO * (1-RATIO)),3)}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(n),2)}',fontsize=15)
print(z_1)
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 대표본 추정' 카테고리의 다른 글
| ★string r'로 받을때 안에 값 집어넣기(변수로도 %2d)★모비율 차의 구간추정★기초통계학-[대표본 추정 -06] (0) | 2023.01.11 |
|---|---|
| ★모평균 차의 구간추정★기초통계학-[대표본 추정 -05] (0) | 2023.01.11 |
| ★신뢰구간★신뢰도★구간추정★기초통계학-[대표본 추정 -03] (0) | 2023.01.11 |
| ★불편추정량★최소분산불편추정량★유효 추정량★불편 추정량★기초통계학-[대표본 추정 -02] (0) | 2023.01.11 |
| ★편의 추정량★불편 추정량★기초통계학-[대표본 추정 -01] (1) | 2023.01.11 |
★신뢰구간★신뢰도★구간추정★기초통계학-[대표본 추정 -03]
1. 구간추정
==> 대표본을 선정하여 모평균 점추정 방식
==> 표본이 어떻게 선정되느냐에 따라 왜곡된 추정값을 얻는 오류 범할 수 있다.
==> 모수의 참값이 포함되리라고 믿어지는 구간을 추정
2. 신뢰구간의 의미
==> 표본으로부터 얻은 점추정이 모수의 참값에 가능한 가깝기를 바라지만, 어느정도로 참값에 가까운지 신뢰할 수 없다.
==> 신뢰도 (1-a)100%에서 모수의 참 값이 포함되리라고 믿어지는 구간
3. 신뢰도
==> 모수의 참값이 추정한 구간 안에 포함될 것으로 믿어지는 미리 정해 놓은 확신의 정도, 일반적으로 (1-a)100%

신뢰구간의 하한 과 상한 사이에 모수의 참값이 포함 가능하다.
==> e는 오차 한계(margin of error) 라고 한다.
EX ) 95%의 신뢰도에서 표본 20개를 임의로 추출
==>이 표본으로부터 얻은 신뢰구간들 중에서 95%에 해당하는 19개 구간이 모평균의 참값을 포함하고 최대 5%에 해당하는 1개의 구간은 모수의 참값을 포함하지 않을 수 있다.
4. 모평균의 신뢰구간
https://knowallworld.tistory.com/302
★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본
1. 표본평균의 표본분포(모분산을 아는 경우) ==> 표본평균에 대한 표본분포는 정규분포를 따른다. EX-01) 모평균 100 , 모분산 9인 정규모집단으로부터 크기 25인 표본을 임의로 추출 1> 표본평균 |X
knowallworld.tistory.com
==> 표본평균의 정규분포화



1> 모평균에 대한 90% 신뢰구간 :
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(0.95) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, '신뢰구간 모평균에 대한 90% : \n' + r'$\overline{X}-{1.645}\dfrac{\sigma}{\sqrt{n}},\overline{X}+{1.645}\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)
2> 모평균에 대한 95% 신뢰구간 :
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf( 1- (1-0.95)/2 ) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, '신뢰구간 모평균에 대한 95% : \n' + r'$\overline{X}-{1.96}\dfrac{\sigma}{\sqrt{n}},\overline{X}+{1.96}\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)

3> 모평균에 대한 99% 신뢰구간 :
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf( 1- (1-0.99)/2 ) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, '신뢰구간 모평균에 대한 99% : \n' + r'$\overline{X}-{2.576}\dfrac{\sigma}{\sqrt{n}},\overline{X}+{2.576}\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)

EX) 전자책에 있는 텍스트 한 쪽을 읽는 데 걸리는 평균 시간에 대한 90% , 95% , 99% 신뢰구간을 구하라.
A= [ 43.2 , 41.5 , 48.3 , 37.7 , 46.8 , 42.6 , 46.7, 51.4 , 47.3 , 40.1 , 46.2 , 44.7]
A ~ N(44.7083 , 8/루트(12) )
1> 평균 시간에 대한 90% 신뢰구간
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-0.9)/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, '신뢰구간 모평균에 대한 90% : \n' + r'$\overline{X}-{1.645}\dfrac{\sigma}{\sqrt{n}},\overline{X}+{1.645}\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)
A = [ 43.2 , 41.5 , 48.3 , 37.7 , 46.8 , 42.6 , 46.7, 51.4 , 47.3 , 40.1 , 46.2 , 44.7]
MEANS = round(np.mean(A) ,2)
STDS = round(math.sqrt(64/len(A)),2)
print((z_1 * STDS / math.sqrt(len(A))))
ax.text(2 , .25, '신뢰구간 모평균에 대한 90% : \n' + f'{round(MEANS - (z_1 * STDS ),2)} ~ {round(MEANS + (z_1 * STDS ),2)}' , fontsize= 15)
ax.text(2 , .35, r'$\overline{X} = $' + f'{MEANS}\n' + r'$\sigma = $' + f'{STDS}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(len(A)),2)}',fontsize=15)
2> 평균 시간에 대한 95% 신뢰구간
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)
A = [ 43.2 , 41.5 , 48.3 , 37.7 , 46.8 , 42.6 , 46.7, 51.4 , 47.3 , 40.1 , 46.2 , 44.7]
MEANS = round(np.mean(A) ,2)
STDS = round(math.sqrt(64/len(A)),2)
print((z_1 * STDS / math.sqrt(len(A))))
ax.text(2 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + f'{round(MEANS - (z_1 * STDS ),2)} ~ {round(MEANS + (z_1 * STDS ),2)}' , fontsize= 15)
ax.text(2 , .35, r'$\overline{X} = $' + f'{MEANS}\n' + r'$\sigma = $' + f'{STDS}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(len(A)),2)}',fontsize=15)
3> 평균 시간에 대한 99% 신뢰구간
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 99 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)
A = [ 43.2 , 41.5 , 48.3 , 37.7 , 46.8 , 42.6 , 46.7, 51.4 , 47.3 , 40.1 , 46.2 , 44.7]
MEANS = round(np.mean(A) ,2)
STDS = round(math.sqrt(64/len(A)),2)
print((z_1 * STDS / math.sqrt(len(A))))
ax.text(2 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + f'{round(MEANS - (z_1 * STDS ),2)} ~ {round(MEANS + (z_1 * STDS ),2)}' , fontsize= 15)
ax.text(2 , .35, r'$\overline{X} = $' + f'{MEANS}\n' + r'$\sigma = $' + f'{STDS}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(len(A)),2)}',fontsize=15)
EX-02) 9명의 어린이가 하루 동안 TV를 시청하는 시간 A = [2.2 , 3.1 , 3.8 , 2.7 , 4.0 , 2.6 , 2.4 , 1.6 , 2.3] , 이 표본을 이용하여 하루동안 TV를 시청하는 평균 시간에 대한 90% , 95% , 99% 신뢰구간을 구하라.(분산이 0.5시간인 정규분포를 따른다.)
|X ~ N(2.744 , 0.5/9)
1> 신뢰구간 90%
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 90 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)
A = [2.2 , 3.1 , 3.8 , 2.7 , 4.0 , 2.6 , 2.4 , 1.6 , 2.3]
MEANS = round(np.mean(A) ,2)
STDS = round(math.sqrt(0.5/len(A)),2)
print((z_1 * STDS / math.sqrt(len(A))))
ax.text(2 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + f'{round(MEANS - (z_1 * STDS ),2)} ~ {round(MEANS + (z_1 * STDS ),2)}' , fontsize= 15)
ax.text(2 , .35, r'$\overline{X} = $' + f'{MEANS}\n' + r'$\sigma = $' + f'{STDS}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(len(A)),2)}',fontsize=15)
2> 신뢰구간 95%

3> 신뢰구간 99%

EX-03) 우리나라 소득액 추정위해 30가구를 표본조사한 결과에 대하여 월평균 소득액의 95% 신뢰구간을 구하라.(표준편차는 3)
A= [91.23, 88.76, 91.19, 90.54, 91.85, 85.07, 90.91, 88.03, 89.22, 89.47, 89.12, 90.48, 91.42, 90.94, 85.65, 85.15, 86.07, 96.35, 90.01, 88.26, 90.5, 87.08, 92.65, 87.05, 85.8, 87.63, 86.66, 83.43, 93.4, 90.17]
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)
ex = '91.23 88.76 91.19 90.54 91.85 85.07 90.91 88.03 89.22 89.47 89.12 90.48 91.42 90.94 85.65 85.15 86.07 96.35 90.01 88.26 90.50 87.08 92.65 87.05 85.80 87.63 86.66 83.43 93.40 90.17'
A = list(map(float, ex.split(' ')))
MEANS = round(np.mean(A) ,2)
STDS = round(math.sqrt(3**2/len(A)),2)
print((z_1 * STDS / math.sqrt(len(A))))
ax.text(2 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + f'{round(MEANS - (z_1 * STDS ),2)} ~ {round(MEANS + (z_1 * STDS ),2)}' , fontsize= 15)
ax.text(2 , .35, r'$\overline{X} = $' + f'{MEANS}\n' + r'$\sigma = $' + f'{STDS}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(len(A)),2)}',fontsize=15)==> 표준오차에 대한 수정하기

EX-04) 우리나라 소득액 추정위해 30가구를 표본조사한 결과에 대하여 월평균 소득액의 95% 신뢰구간을 구하라.(표준편차는 5.105)
A = [93.242, 89.635, 92.66, 92.54, 94.883, 102.165, 93.326, 90.88, 93.684, 91.564, 88.727, 94.317, 88.166, 96.085, 82.028, 97.213, 99.338, 93.381, 86.498, 83.348, 97.262, 89.656, 84.045, 89.113, 81.562, 87.18, 94.345, 92.436, 93.633, 97.276]
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)
ex = '93.242 89.635 92.660 92.540 94.883 102.165 93.326 90.880 93.684 91.564 88.727 94.317 88.166 96.085 82.028 97.213 99.338 93.381 86.498 83.348 97.262 89.656 84.045 89.113 81.562 87.180 94.345 92.436 93.633 97.276'
A = list(map(float, ex.split(' ')))
MEANS = round(np.mean(A) ,3)
VARS = 5.105**2
STDS = round(math.sqrt(VARS/len(A)),3)
print((z_1 * STDS / math.sqrt(len(A))))
ax.text(2 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + f'{round(MEANS - (z_1 * STDS ),3)} ~ {round(MEANS + (z_1 * STDS ),3)}' , fontsize= 15)
ax.text(2 , .35, r'$\overline{X} = $' + f'{MEANS}\n' + r'$\sigma = $' + f'{STDS}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(len(A)),2)}',fontsize=15)
==>이 표본으로부터 얻은 신뢰구간들 중에서 95%에 해당하는 구간이 모평균의 참값을 포함하고 최대 5%에 해당하는 구간은 모수의 참값을 포함하지 않을 수 있다.
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 대표본 추정' 카테고리의 다른 글
| ★string r'로 받을때 안에 값 집어넣기(변수로도 %2d)★모비율 차의 구간추정★기초통계학-[대표본 추정 -06] (0) | 2023.01.11 |
|---|---|
| ★모평균 차의 구간추정★기초통계학-[대표본 추정 -05] (0) | 2023.01.11 |
| ★모비율의 신뢰구간★기초통계학-[대표본 추정 -04] (0) | 2023.01.11 |
| ★불편추정량★최소분산불편추정량★유효 추정량★불편 추정량★기초통계학-[대표본 추정 -02] (0) | 2023.01.11 |
| ★편의 추정량★불편 추정량★기초통계학-[대표본 추정 -01] (1) | 2023.01.11 |
★불편추정량★최소분산불편추정량★유효 추정량★불편 추정량★기초통계학-[대표본 추정 -02]
1. 유효추정량
==> 일반적으로 절사평균은 모평균에 대한 불편추정량이 아니다.
https://knowallworld.tistory.com/213
np.median★절사평균, 중위수★기초통계학-[Chapter03 - 03]
1. 절사평균 A = [1,2,3,4,5] 의 산술평균 : 3 B = [1,2,3,4,50]의 산술평균 : 12 ==> 산술평균은 특이점(_50_) 과 같이 유무에 따라 많은 영향을 받는다. ==> 특이점 있을경우 특이점 제거한다면 특이점의 영향
knowallworld.tistory.com
==> 절사평균은 특이점을 제거한 평균 사용 ==> 보편적으로 양쪽 끝 5%~10% 절사
==> 표본 중위수도 모집단 중위수에 대한 불편추정량이 되지 못한다.
https://knowallworld.tistory.com/211
★모평균, 표본평균★중심위치의 척도★기초통계학-[Chapter03 - 01]
1. 중심위치의 척도 ==> 원자료를 의미 있는 형태로 정리하기 위해 도수분포표를 작성하여 결과를 히스토그램 또는 도수다각형의 그림으로 나타냄 ==> 자료가 집중하는 경향을 수치로 나타내는
knowallworld.tistory.com
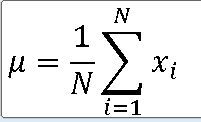

표본평균 |X = 모평균 M
==> 모평균 M에 대한 불편추정량
https://knowallworld.tistory.com/305
★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집
1. 모분산의 표본분포 정규모집단 N(뮤 , 모분산) 으로부터 크기 n인 표본을 선정할 때 표본분산 ==> 표본분산 S**2에 대한 표본분포는 X**2-통계량 V에 대하여 자유도가 n-1인 카이제곱분포이다. https:
knowallworld.tistory.com



표본분산 s**2 은 모분산에 대한 불편 추정량
https://knowallworld.tistory.com/306
이항분포에 따른 정규분포의 표준정규분포화★표본비율의 표본분포★기초통계학-[모집단 분포
1.표본비율의 표본분포 EX) 이항 확률변수의 실질적인 응용 ==> 여론조사 생각 ==> 모집단을 구성하는 사람들의 어느 특정 사건을 선호하는 비율(p)를 알기 위하여 n명으로 구성된 표본을 임의 선정
knowallworld.tistory.com

==> 표본비율은 모비율 p에 대한 불편추정량
WHY 표본분산을 정의 할때 n-1을 하는가!!!
E(S**2) = (n-1)/ n * 모분산 != 모분산
==> 크기 n-1로 나누어야 불편성을 갖으므로 표본분산을 정의 할때 n-1로 나누어 정의한다.
유효추정량 : 추정량의 표본분포가 모수의 참값에 가장 가깝게 분포하는 경우, 즉 가장 작은 분산을 갖는 추정량이다.
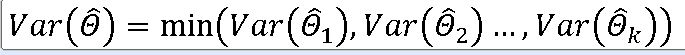
표준오차 : 모수를 추정하기 위해 사용되는 추정량의 표준편차

EX-01) 모평균이 M(뮤) 인 모집단에서 크기 3인 확률표본 {X_1 , X_2 , X_3}을 추출 , 모평균에 대한 불편추정량 중에서 유효성을 갖는 추정량
^M_1 = (1/3)* (X_1 + X_2 + X_3)
^M_2 = (1/4) * ( (2* X_1) + X_2 + X_3)
^M_3 = (1/5) * ( X_1 + (2* X_2) + (2* X_3 ) )
^M_4 = (1/5) * ( X_1 +(2* X_2 ) + X_3)
==> X_1, X_2 , X_3이 동일한 모집단 분포를 따르므로 Var(X_1) = Var(X_2) = Var(X_3)= 모분산
https://knowallworld.tistory.com/255
★정규분포의 표준정규분포로의 변환★추측통계학-[Chapter06 - 연속확률분포-04]
1. 확률변수 X와 Y에 대한 분산 2. 서로 독립인 확률변수 X와 Y가 정규분포 X ~N(뮤_1 , 분산) , Y~ N(뮤_2 , 분산) 따르는 경우의 추측통계학 EX-01) X는 N(1995 , 144) Y는 N(1755 , 100) 1> X-Y의 확률분포 X-Y ~ N(1995
knowallworld.tistory.com

Var(^M_1) = (1/9)* Var(X_1 + X_2 + X_3) = (1/9) * (모분산 + 모분산 + 모분산) = (1/3) * 모분산
Var(^M_2) = (1/16) * Var(2*X_1 + X_2 + X_3) = (1/16) * Var(4*모분산 + 모분산 + 모분산) = (3/8)*모분산
Var(^M_3) = (1/25) * Var(X_1 + 2*X_2 + 2*X_3 ) = (1/25) * Var(모분산 + 4*모분산 + 4*모분산) = (9/25) * 모분산
Var(^M_2) > Var(^M_3) > Var(^M_1)
==> 유효추정량은 Var(^M_1) 이다.
EX-02) 모평균이 M(뮤) 인 모집단에서 크기 2인 확률표본 {X_1 , X_2}을 추출 , 모평균에 대한 불편추정량 중에서 유효성을 갖는 추정량
^M_1 = X_1
^M_2 = (1/2) * (X_1 +X_2)
^M_3 = (1/2) * (X_1 + 2*X_2)
^M_4 = (1/3) * (X_1 + 2*X_2)
==> ^M_1 , ^M_2 , ^M_4 ==> 불편추정량
Var(^M_1) = Var(X_1) = 1*모분산
Var(^M_2) = (1/4)* Var(X_1 + X_2) = (1/4)* (Var(X_1) + Var(X_2) ) = (1/2) * 모분산
Var(^M_4) = (1/9) * Var(X_1 + 2*X_2) = (1/9) * ( Var(X_1) + 4Var(X_2) ) = (5/9)* 모분산
Var(^M_2) < Var(^M_3) < Var(^M_1)
==> Var(^M_2) 가 유효추정량
2. 최소분산불편추정량(Minimum Variance unbiased estimator)
==> 모두에 대한 불편성과 유효성을 모두 갖는 추정량이다.
x = np.arange(-1,1 ,.001)
fig = plt.figure(figsize= (15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale = math.sqrt(1/10))) #정의역 범위 , 표본평균의 평균 = 0 , 표본평균의 분산 =1/10 인 정규분포 플롯
plt.annotate('' , xy=(0.5, .5), xytext=(.75 , .5) , arrowprops = dict(facecolor = 'black'))
ax.text(0.75 , 0.5 , r'n = 10' , fontsize = 13)
sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale= math.sqrt(1/20))) #정의역 범위 , 표본평균의 평균 = 0 , 표본평균의 분산 =1/20 인 정규분포 플롯
plt.annotate('' , xy=(0.25, 1.1), xytext=(.4 , 1.5) , arrowprops = dict(facecolor = 'black'))
ax.text(0.4 , 1.5 , r'n = 20' , fontsize = 13)
sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =math.sqrt(1/50))) #정의역 범위 , 표본평균의 평균 = 0 , 표본평균의 분산 =1/50 인 정규분포 플롯
plt.annotate('' , xy=(-0.16, 1.5), xytext=(-.25 , 2) , arrowprops = dict(facecolor = 'black'))
ax.text(-0.35 , 2.1 , r'n = 50' , fontsize = 13)
sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =math.sqrt(1/100))) #정의역 범위 , 표본평균의 평균 = 0 , 표본평균의 분산 =1/100 인 정규분포 플롯
ax.axvline(x= 0, ymin=0 , ymax=1 , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
plt.annotate('' , xy=(-0.08, 3), xytext=(-.25 , 3) , arrowprops = dict(facecolor = 'black'))
ax.text(-0.35 , 3.1 , r'n = 100' , fontsize = 13)
ax.text(0, .41, f'평균 : {round(0,2)}',fontsize=13)
plt.legend(['N(0,1/10)' , 'N(0,1/20)' , 'N(0,1/50)' , 'N(0,1/100)' ] , fontsize = 15)
EX-01) 성인이 전자책에 있는 텍스트 한 쪽을 읽는 데 걸리는 평균 시간을 추정하기 위하여 다음과 같이 12명을 임의로 선정하여 시간을 측정하였다. 이때 텍스트 한 쪽을 읽는 데 걸리는 시간은 표준편차가 8초인 정규분포를 따른다고 알려졌다. 이 표본을 이용하여 성인이 텍스트 한 쪽을 읽는 데 걸리는 평균시간을 추정하고, 표준오차를 구하라.
A= [ 43.2 , 41.5 , 48.3 , 37.7 , 46.8 , 42.6 , 46.7, 51.4 , 47.3 , 40.1 , 46.2 , 44.7]
평균 _|A = 44.7083
A ~ N(44.7083 , 8/루트(12) )
s = 8

|X의 표준편차(오차) = 8 /루트(12) = 2.31
EX-02) 9명의 어린이가 하루 동안 TV를 시청하는 시간 A = [2.2 , 3.1 , 3.8 , 2.7 , 4.0 , 2.6 , 2.4 , 1.6 , 2.3] , 이 표본을 이용하여 하루동안 TV를 시청하는 평균 시간을 추정하고, 표준오차를 구하라.(분산이 0.5시간인 정규분포를 따른다.)
A ~ N(뮤 , 0.5)
==> |A가 모평균에 대한 최소분산불편추정량이므로 표본평균을 구할 수 있다.

|A ~ N(2.744 , 0.5/9)
A = [2.2 , 3.1 , 3.8 , 2.7 , 4.0 , 2.6 , 2.4 , 1.6 , 2.3]
MEANS = np.mean(A)
print(MEANS)
print(math.sqrt(0.5/9))시청 평균시간 = 2.744
|A의 표준편차 = 루트(0.5/9) = 0.2357
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 대표본 추정' 카테고리의 다른 글
| ★string r'로 받을때 안에 값 집어넣기(변수로도 %2d)★모비율 차의 구간추정★기초통계학-[대표본 추정 -06] (0) | 2023.01.11 |
|---|---|
| ★모평균 차의 구간추정★기초통계학-[대표본 추정 -05] (0) | 2023.01.11 |
| ★모비율의 신뢰구간★기초통계학-[대표본 추정 -04] (0) | 2023.01.11 |
| ★신뢰구간★신뢰도★구간추정★기초통계학-[대표본 추정 -03] (0) | 2023.01.11 |
| ★편의 추정량★불편 추정량★기초통계학-[대표본 추정 -01] (1) | 2023.01.11 |
★편의 추정량★불편 추정량★기초통계학-[대표본 추정 -01]
1. 점추정
==> 임의의 모집단으로부터 대표본을 추출하면 중심극한정리에 의해 표본평균은 정규분포에 근사한다.
https://knowallworld.tistory.com/304
★중심극한정리★기초통계학-[모집단 분포와 표본분포 -05]
EX-01) 남성의 평균 결혼연령 32세 , 분산 8.41세 , 36명 임의로 선정하여 표본조사 1> 평균 결혼 연령의 근사 표본분포 n = 36 >= 30 이므로 중심극한 정리에 의하여 평균결혼 연령은 |X ~ N(32 , 8.41/ 36) 2>
knowallworld.tistory.com
==> but. 보통 모수는 알려져 있지 않다. 따라서 임의로 선정한 표본을 이용하여 알려지지 않은 모수를 보편적이고 타당한 방법으로 추정해야 한다.
==> 표본으로부터 얻은 정보를 이용하여 알려지지 않은 모집단의 정보를 추론하는 것이 추측통계학의 목적
2. 점추정의 의미
==> 통계적 추론(Statistical inference)는 표본으로부터 얻은 정보를 이용하여 과학적으로 미지의 모수를 추론하는 과정
==> 모평균 , 모분산 , 모비율 등과 같은 모수를 추론하기 위해, 크기 n인 표본을 추출하여 표본평균, 표본분산, 표본비율 등을 산출
==> 추출된 표본에 대한 표본평균, 표본분산, 표본비율과 같은 통계량의 측정값을 산출하여 미지의 모집단 분포와 모수를 추론하는 과정을 추정이라 한다.
==> 모수를 추정하기 위하여 표본으로부터 얻은 통계량을 추정량이라 한다.


==> 점추정량은 모수를 추정하기 위하여 표본에 기초에 어떤 하나의 수치를 계산하는 규칙 또는 함수 의미
==> 점추정은 모수를 추론하기 위하여 점추정량에 의해 얻은 수치
3. 바람직한 점추정
==> 바람직한 추정량이 되기 위해서는 2가지 조건이 필요
==> 추정하고자 하는 모수에 대한 추정량의 표본분포가 모수의 참값을 중심으로 이루어져야 한다.
==> 이 추정량의 표준편차가 가장 작은 것
4. 불편 추정량
==> 추정량의 평균이 모수의 참값과 같은 추정량

==> 정규분포를 포함한 임의의 모집단 분포에서 크기 n인 표본을 임의로 선정하면, 표본평균 |X의 평균은 모평균과 동일하다.
https://knowallworld.tistory.com/302
★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본
1. 표본평균의 표본분포(모분산을 아는 경우) ==> 표본평균에 대한 표본분포는 정규분포를 따른다. EX-01) 모평균 100 , 모분산 9인 정규모집단으로부터 크기 25인 표본을 임의로 추출 1> 표본평균 |X
knowallworld.tistory.com



==> 표본평균 |X는 모평균에 대한 불편추정량이다.
5. 편의 추정량
==> 불편추정량이 아닌 추정량을 편의(bias)라 한다.

EX-01) 모평균이 M(뮤) 인 모집단에서 크기 3인 확률표본 {X_1 , X_2 , X_3}을 추출하여, 모평균에 대한 점추정량을 다음과 같이 정의하였다. 모평균 M(뮤)에 대한 불편추정량과 편의추정량을 구별하라.
^M_1 = (1/3)* (X_1 + X_2 + X_3)
^M_2 = (1/4) * ( (2* X_1) + X_2 + X_3)
^M_3 = (1/5) * ( X_1 + (2* X_2) + (2* X_3 ) )
^M_4 = (1/5) * ( X_1 +(2* X_2 ) + X_3)
==> X_1 , X_2 , X_3 이 동일한 모집단 분포를 따르므로 E(X_1) = E(X_2) = E(X_3) = M(뮤) 이다.
==>E(^M_1) = (1/3)* E(X_1+ X_2 + X_3) = (1/3)*[E(X_1) + E(X_2) + E(X_3) ] = (1/3) * (M + M + M ) = M
==>E(^M_2) = (1/4)* E( (2* X_1) + X_2 + X_3) = (1/3)*[ (2* E(X_1) ) + E(X_2) + E(X_3) ] = (1/4) * (2* M + M + M ) = M
==>E(^M_3) = (1/5)* E(X_1+ (2* X_2) + (2 * X_3) ) = (1/5)*[E(X_1) + (2* E(X_2) ) + (2 * E(X_3 ) ) ] = (1/5) * (M + 2*M + 2* M ) = M
==>E(^M_4) = (1/5)* E(X_1+ (2* X_2) + X_3) = (1/5)*[E(X_1) + (2* E(X_2) ) + E(X_3) ] = (1/5) * (M + 2*M + M ) = 4*M / 5
==> ^M_1 , ^M_2 , ^M_3 ==> 모평균에 대한 불편추정량
==> ^M_4 ==> 모평균에 대한 편의추정량
EX-02) 모평균이 M(뮤) 인 모집단에서 크기 2인 확률표본 {X_1 , X_2}을 추출하여, 모평균에 대한 점추정량을 다음과 같이 정의하였다. 모평균 M(뮤)에 대한 불편추정량과 편의추정량을 구별하라.
^M_1 = X_1
^M_2 = (1/2) * (X_1 +X_2)
^M_3 = (1/2) * (X_1 + 2*X_2)
^M_4 = (1/3) * (X_1 + 2*X_2)
==> X_1 , X_2 이 동일한 모집단 분포를 따르므로 E(X_1) = E(X_2) = M(뮤) 이다.
==> E(^M_1) = E(X_1) = M (불편추정량)
==> E(^M_2) = (1/2) * E(X_1 + X_2) = (1/2) * (E(X_1) + E(X_2) ) = M(불편추정량)
==> E(^M_3) = (1/2) * E(X_1 + 2*X_2) = (1/2) * (E(X_1) + 2*E(X_2) ) = 3/2 * M (편의 추정량)
==> E(^M_4) = (1/3) * E(X_1 + 2*X_2) = (1/3) * (E(X_1) + 2*E(X_2) ) = M(불편추정량)
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 대표본 추정' 카테고리의 다른 글
| ★string r'로 받을때 안에 값 집어넣기(변수로도 %2d)★모비율 차의 구간추정★기초통계학-[대표본 추정 -06] (0) | 2023.01.11 |
|---|---|
| ★모평균 차의 구간추정★기초통계학-[대표본 추정 -05] (0) | 2023.01.11 |
| ★모비율의 신뢰구간★기초통계학-[대표본 추정 -04] (0) | 2023.01.11 |
| ★신뢰구간★신뢰도★구간추정★기초통계학-[대표본 추정 -03] (0) | 2023.01.11 |
| ★불편추정량★최소분산불편추정량★유효 추정량★불편 추정량★기초통계학-[대표본 추정 -02] (0) | 2023.01.11 |
★표본비율차이에 따른 표준정규분포★기초통계학-[연습문제02 -21]
32. 여자의 27%와 남자의 22%가 어느 특정 브랜드의 커피를 좋아한다고 주장한다. 여자와 남자를 동일하게 250명씩 임의로 선정하여 조사한 결과, 여자 중에서 69명, 남자중에서 58명이 좋아한다고 응답하였다.
1> 여자와 남자의 표본비율의 차 $ \widehat{P}_{1} $ - $ \widehat{P}_{2} $에 대한 근사 확률분포를 구하라.
https://knowallworld.tistory.com/311
★표본비율의 차에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -12]
1. 두 표본비율의 차에 대한 표본분포 ==> 서로 독립이고 모비율이 각각 p_1 , p_2인 두 모집단에서 각각 크기 n,m인 표본 선정 ==> 표본의 크기가 충분히 크다면 https://knowallworld.tistory.com/301 ★모비율
knowallworld.tistory.com


m = n = 250
$ {p}_{1} $ = 0.27
$ {p}_{2} $ = 0.22
$ \dfrac{p_{1}q_{1}}{n} $ + $ \dfrac{p_{2}q_{2}}{n} $ = 0.27*0.73 / 250 + 0.22*0.78 / 250 = 0.00147
$ \widehat{p}_{1}-\widehat{p}_{2} $ ~ N(0.05 , $ \sqrt{0.00147} $ )
2> $ \widehat{P}_{1} $ - $ \widehat{P}_{2} $ 가 3% 보다 작을 근사 확률
P($ \widehat{P}_{1} $ - $ \widehat{P}_{2} $ < 0.03) = P(Z< 0.03 - 0.05 / 루트(0.00147) ) = P(Z<= -0.52) = 0.6985
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.03-0.05) / math.sqrt(0.00147) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
# z_1 = round(scipy.stats.norm.ppf(1- 0.025) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- scipy.stats.norm.cdf(z_1)
ax.text(0 , .12, f'P(Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(-1.3, .1), xytext=(0 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))

3> $ \widehat{P}_{1} $ - $ \widehat{P}_{2} $ 가 관찰된 표본비율의 차보다 클 근사 확률
관찰된 표본비율
여자 : 69 / 250
남자 : 58 / 250
P( $ \widehat{P}_{1} $ - $ \widehat{P}_{2} $ > (69/250 - 58/250) ) = P(Z > (69/250 - 58/250) - 0.05) / 루트(0.00147) ) = P(Z>=-0.16) = 0.5636
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((69/250 - 58/250 - 0.05) / math.sqrt(0.00147) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
# z_1 = round(scipy.stats.norm.ppf(1- 0.025) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- scipy.stats.norm.cdf(z_1)
ax.text(-1.5 , .12, f'P(Z>={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .1), xytext=(-1.3 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
4> $ \widehat{p}_{1} $ - $ \widehat{p}_{2} $ 가 $ {p}_{0} $ 보다 클 확률이 0.025인 $ {p}_{0} $를 구하라.
P(Z> (p_0 - 0.05) / 루트(0.00147) ) = P(Z>= 1.96) =0.025
$ {p}_{0} $ = 0.1251
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
# z_1 = round((69/250 - 58/250 - 0.05) / math.sqrt(0.00147) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1-0.025) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- scipy.stats.norm.cdf(z_1)
ax.text(.3 , .03, f'P(Z>={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.2, .01), xytext=(1.3 , .01) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
p = Symbol('p')
b = solve(1.96 * math.sqrt(0.00147) + 0.05 - p)
print(b)

33. 25세 이상 남자와 여자 중 대졸 이상은 각각 37.8% , 25.4%로 조사되었다. 남자와 여자를 각각 500명, 450명씩 표본조사한 결과, 남자와 여자 비율의 차가 10%이하일 확률

p_1 = 0.378
n = 500
p_2 = 0.254
m = 450
^p_1 - ^p_2 ~ N(0.378-0.254 , 0.378*(1-0.378) / 500 + 0.254*(1-0.254)/450 )
P(^p_1 - ^p_2 <= 0.1) = P(Z <= (0.1 - (0.378-0.254)) / 루트(0.378*(1-0.378) / 500 + 0.254*(1-0.254)/450) ) = P(Z<= -0.8) = 0.2119
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.1 - 0.378+0.254) / math.sqrt( (0.378)*(1-0.378)/500 + 0.254 *(1-0.254)/450 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
# z_1 = round(scipy.stats.norm.ppf(1-0.025) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1)
ax.text(-.2 , .09, f'P(Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(-1.5, .1), xytext=(-.3 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))

34. 중국 131명중 93.9% , 북미 및 유럽 48명중 93.8%, 두 지역의 외국인 주민의 한국어 교육을 받을 의향이 동일하게 93%가 그렇다고 응답.
1>중국과 북미 및 유럽 외국인 주민의 표본비율의 차 ^p_1 - ^p_2에 대한 근사 확률분포
^p_1 - ^p_2 ~ N(0 , 0.93*(0.07) / 131 + 0.93*(0.07) / 48 ) = N(0 , 0.0018532)
2>^p_1 - ^p_2가 5%보다 작을 근사 확률
P(^p_1 - ^p_2 <= 0.05) = P(Z<= (0.05-0) / 루트(0.0018532) ) = P(Z<=1.16) = 0.877
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
# z_1 = round(scipy.stats.norm.ppf(1-0.025) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1)
ax.text(2 , .1, f'P(Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))

3>^p_1 - ^p_2가 관찰된 표본비율의 차보다 클 근사 확률
P(^p_1 - ^p_2 > 0.939 - 0.938) = P(Z> = (0.001 - 0)/루트( 0.0018532) ) = P(Z>=0.02) = 0.508
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.001) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
# z_1 = round(scipy.stats.norm.ppf(1-0.025) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- scipy.stats.norm.cdf(z_1)
ax.text(2 , .1, f'P(Z>={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0.5, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
4>^p_1 - ^p_2가 p_0보다 클 확률이 0.05인 p_0를 구하라.
P(^p_1 - ^p_2 > p_0) = 0.05
P(Z> p_0/루트(0.0018532) ) = P(Z>=1.64) =0.05
p_0 = 0.0706
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
# z_1 = round((0.001) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1-0.05) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- scipy.stats.norm.cdf(z_1)
ax.text(2 , .1, f'P(Z>={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2, .01), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
t = Symbol('t')
e = solve(1.64 * math.sqrt(0.0018532) - t)
print(e)
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
★종합선물세트★F-분포(표본분산의 비 이용!)★표본평균의 차에 따른 확률분포!★합동표본분산 구하는 법!★모분산을 모를땐 t-분포★모분산을 알때는 카이제곱분포★기초통계학-[연습문제..
29. 두 정규모집단 A와 B의 모분산은 동일하고, 평균은 각각 뮤_1 = 700 , 뮤_2 = 680이라 한다. 두 모집단으로 부터 표본을 추출하여 A 표본 [n = 17 , |x = 704 , s_1 = 39.25] , B표본 [m = 10 , |y = 675 , s_2 = 43.75]
https://knowallworld.tistory.com/309
★서로독립인 정규집단의 표본분산(모분산은 알때) 추론★카이제곱분포★합동표본분산에 대한
1. 합동표본분산에 대한 표본분포 ==> 동일한 모분산을 갖는 서로 독립인 두 정규 모집단 ==> 크기가 n과 m인 두 확률표본 추출 ==>두 표본의 표본분산에 대한 합동표본분산 정의 https://knowallworld.tist
knowallworld.tistory.com

https://knowallworld.tistory.com/308
★두 표본평균의 차에 대한 표본분포(모분산 모를때)★중심극한정리 활용★이표본의 표본분포
1. 두 표본평균의 차에 대한 표본분포(두 모분산을 모르는 경우) https://knowallworld.tistory.com/302 ★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본 1. 표
knowallworld.tistory.com
1> 두 표본에 대한 합동표본분산 s_p**2을 구하라.
s_p**2 = 1/(17+10-2) * (16*(39.25**2) + 9*(43.75**2) ) = 1675.0225
2> 두 표본평균의 차 T = |X - |Y 에 대한 확률분포를 구하라.
https://knowallworld.tistory.com/307
★두 표본평균의 차에 대한 표본분포(모분산 알때 , 동일할때)★중심극한정리 활용★이표본의
1. 이표본의 표본분포 ==>지금까지는 단일 모집단의 표본에 대한 통계량의 표본분포 EX) 수능에서 남학생, 여학생 집단의 평균이 동일한지 여부 비교 ==> 비교위해서는 각각 표본을 추출하여야 한
knowallworld.tistory.com

|X의 평균 = 704
분산 = 39.25**2
N = 17
|Y의 평균 = 675
분산 = 43.75**2
M = 10
모평균_|X-모평균_|Y = 20
s_|x-|y = 루트(1675.0225) * (루트(1/17 + 1/10) )
(T-20) / (루트(1675.0225) * (루트(1/17 + 1/10) ) ~ T(25)
https://knowallworld.tistory.com/259
★scipy.stats.t(자유도).ppf()★t-분포★기초통계학-[Chapter06 - 연속확률분포-07]
1. T-분포(Chi-square Distribution) ==> T-분포는 모분산이 알려지지 않은 정규모집단의 모평균에 대한 추론 ==>서로 독립인 표준정규화확률변수 Z와 자유도 n인 카이제곱 확률변수 V에 대하여 정의 ==> T ~
knowallworld.tistory.com
==> 모분산을 모를땐 t-분포! , 알때는 카이제곱분포(표본분산 추정)
==> χ²분포는 정규분포를 따르는 변수의 분산을 분석할 때 사용
==>T분포는 모분산을 모르는 경우에 표본분산을 이용해서 분석할 때 사용
3> P(T>t_0) = 0.05인 t_0를 구하라.
X = np.arange(-5,5 , .01)
fig = plt.figure(figsize=(15,8))
dof_2 = [25] #자유도
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
t_r = scipy.stats.t(dof_2).ppf(1- 0.05)
print(t_r)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
plt.annotate('' , xy=(3.0, .007), xytext=(2.5 , .16) , arrowprops = dict(facecolor = 'black'))
ax.text(1.71 , .17, r'$P(T>t_{0.05})$' + f'= {0.05}',fontsize=15)
ax.text(t_r - 1 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
t = Symbol('t')
a = solve( (t - 20)/ (math.sqrt(1675.0225)* math.sqrt(1/17 + 1/10)) - 1.708)
print(a)
30. 환자 32명을 두 그룹으로 분할, 평균수치가 높을수록 치료의 효과가 있다. 치료법 A = [n=14 , |x = 47.20 , s_2**2 = 111.234] , 치료법 B = [m = 18 , |y = 43.43 , s_1**2 = 105.252]
1> 두표본에 대한 합동표본분산을 구하라.
s_p**2 = (1/ n+m-2) * ( (n-1)*s_1**2 + (m-1)*s_2**2 ) = (1/30) * (13*111.234 + 17*105.252) = 107.8442
2> 뮤_1 = 뮤_2 라 할 때 , 이 표본에 기초하여 P(|X - |Y > 10.175)를 구하라.
|X의 평균 = 47.20
n = 14
s_2 = 루트(111.234)
|Y의 평균 = 43.43
m = 18
s_1 = 루트(105.252)
자유도 = 32 - 2 = 30
모평균_|x - 모평균_y = 0(모평균이 같다!)
분산_|X-|Y = 루트(107.8442) * 루트(1/14 + 1/18)
t_r = round( (10.715 - (0)) / (math.sqrt(107.8442) * math.sqrt(1/14 + 1/18)), 3)P(T > [10.715 - (0)] / 분산_|X-|Y) = P(T> t_0.004) = P(T>2.895) = 0.004
X = np.arange(-5,5 , .01)
fig = plt.figure(figsize=(15,8))
dof_2 = [30] #자유도
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
# t_r = scipy.stats.t(dof_2).cdf(1- 0.05)
t_r = round( (10.715 - (0)) / (math.sqrt(107.8442) * math.sqrt(1/14 + 1/18)), 3)
print(t_r)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
plt.annotate('' , xy=(3.0, .007), xytext=(2.5 , .16) , arrowprops = dict(facecolor = 'black'))
area = 1- scipy.stats.t(dof_2).cdf(t_r)
ax.text(1.71 , .17, r'$P(T>t_{0.004})$' + f'= {area}',fontsize=15)
ax.text(t_r - 1 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
3> 모분산_|x = 모분산_|y = 102일때, 합동표본분산이 62.87보다 클 확률
|X의 평균 = 47.20
n = 14
s_2 = 루트(111.234)
|Y의 평균 = 43.43
m = 18
s_1 = 루트(105.252)
자유도 = 32 - 2 = 30
==>모분산 안다?! ==> 카이제곱 분포
https://knowallworld.tistory.com/309
★서로독립인 정규집단의 표본분산(모분산은 알때) 추론★카이제곱분포★합동표본분산에 대한
1. 합동표본분산에 대한 표본분포 ==> 동일한 모분산을 갖는 서로 독립인 두 정규 모집단 ==> 크기가 n과 m인 두 확률표본 추출 ==>두 표본의 표본분산에 대한 합동표본분산 정의 https://knowallworld.tist
knowallworld.tistory.com

V = (n-1)*s_p**2 / 모분산
x = 30/102* S_p**2 ~ X**2(30)
P(S**2 > 62.87) = P(30/102*S**2 > 30 * 62.87 / 102) = P(X>= 18.49) = 0.95
4> 모분산_|x = 모분산_|y = 102일때, P(S_1**2 > 0.4*S_2**2) 를 구하라.(답지가 이상하다?!)
|X의 평균 = 47.20
n = 14
s_2 = 루트(111.234)
|Y의 평균 = 43.43
m = 18
s_1 = 루트(105.252)
https://knowallworld.tistory.com/310
★F-분포★두 표본분산의 비에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -11]
1. 두 표본분산의 비에 대한 표본분포 ==> 서로 독립인 두 정규모집단의 모분산이 다를때, 모분산 중에서 어느 것이 더큰지 비교하는 경우 ==> 모분산은 양수이므로, 두 모분산의 비의 값을 이용하
knowallworld.tistory.com

==> 서로 독립인 두 모집단의 모분산이 동일한지 아닌지를 통계적으로 추론
==> 모분산 동일하지 않을 때 표본분포 값 구한다.
(S_1**2 / 모분산_1) / (S_2**2/ 모분산_2) = (S_1**2) / (S_2**2) ~ F(13,17)
P(S_1**2 > 0.4*S_2**2) = P(S_1**2 / S_2**2 > 0.4) = P(F>0.4) = 0.95(답지가 이상)
X = np.arange(0,10, .01)
fig = plt.figure(figsize = (15,8))
dof = [[13,17]]
#print(dof[0][0])
for i in dof:
ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
b = ['F({},{})'.format(i,j) for i,j in dof]
X_r = 0.4
print(X_r)
# X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(0.04)
# ax.fill_between(X, scipy.stats.f(dof[0][0],dof[0][1]).pdf(X) , where = (X>=X_r) | (X<=X_l) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
ax.fill_between(X, scipy.stats.f(dof[0][0],dof[0][1]).pdf(X) , where = (X>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
ax.vlines(X_r , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_r) , color = 'black')
# ax.vlines(X_l , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_l) , color = 'black')
area = round(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_r) ,2 )
# ax.annotate('' , xy=(X_l -0.02 , 0.1) , xytext=(X_l + 0.5 , 0.1) , arrowprops = dict(facecolor = 'black'))
# ax.text(X_l + 0.5 , 0.1 , r'$P(F\leqq f_{0.95,4,5})$' + f'= {0.05}' , fontsize = 14)
ax.annotate('' , xy=(X_r +0.3 , 0.01) , xytext=(X_r + 0.3 , 0.2) , arrowprops = dict(facecolor = 'black'))
ax.text(X_r + 0.3 , 0.21 , r'$P(F\geqq f_{0.95,13,17}$' + f'= {area}' , fontsize = 14)
# ax.text(X_l + 0.05 , 0.01 , r'$f_{0.95,4,5}$)' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(0.05) ,2)}' ,fontsize = 13)
ax.text(X_r - 1.3 , 0.01 , r'$f_{0.95,13,17}$' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- area) , 2)}' ,fontsize = 13)
plt.legend(b , fontsize= 15)
31. 시중에서 판매되고 있는 두 회사의 커피믹스에 포함된 카페인의 양을 조사, 제조된 커피믹스에 포함된 카페인의 양은 동일한 분산을 갖는 정규분포 A= [n = 16 , |x = 78 , s_1**2 = 32.5] , B = [m =16 , |y = 75 , s_2**2 = 34.2]
1> 두 표본에 대한 합동표본분산
s_p**2 = (1/ n+m-2) * ( (n-1)*s_1**2 + (m-1)*s_2**2 ) = (1/30) * (15*32.5 + 15*34.2) = 33.35
2> 모평균_A = 모평균_B 일 때 , P(|X-|Y > x_0 ) = 0.01을 만족하는 x_0을 구하라.
모분산 모른다! ==> t-분포 활용
모평균_A - 모평균_B = 0
(T - 0) / (루트(33.35) * 루트(1/16 + 1/16) ) ~ t(30)
P(T > x_0/(루트(33.35) * 루트(1/16 + 1/16) ) ) = 0.01
P(T>2.457) = 0.01
x_0 / (루트(33.35) * 루트(1/16 + 1/16) ) = 2.457
x_0 = 5.016
X = np.arange(-5,5 , .01)
fig = plt.figure(figsize=(15,8))
dof_2 = [30] #자유도
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
t_r = scipy.stats.t(dof_2).ppf(1-0.01)
# t_r = round( (x_0 - (0)) / (math.sqrt(33.463) * math.sqrt(1/16 + 1/16)), 3)
print(t_r)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
plt.annotate('' , xy=(3.0, .007), xytext=(2.5 , .16) , arrowprops = dict(facecolor = 'black'))
area = 1- scipy.stats.t(dof_2).cdf(t_r)
ax.text(1.71 , .17, r'$P(T>t_{0.01})$' + f'= {area}',fontsize=15)
ax.text(t_r - 1 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
t = Symbol('t')
a = solve( t- 2.457 * (math.sqrt(33.35)* math.sqrt(1/16 + 1/16)))
print((math.sqrt(33.35)* math.sqrt(1/16 + 1/16)))
print(a)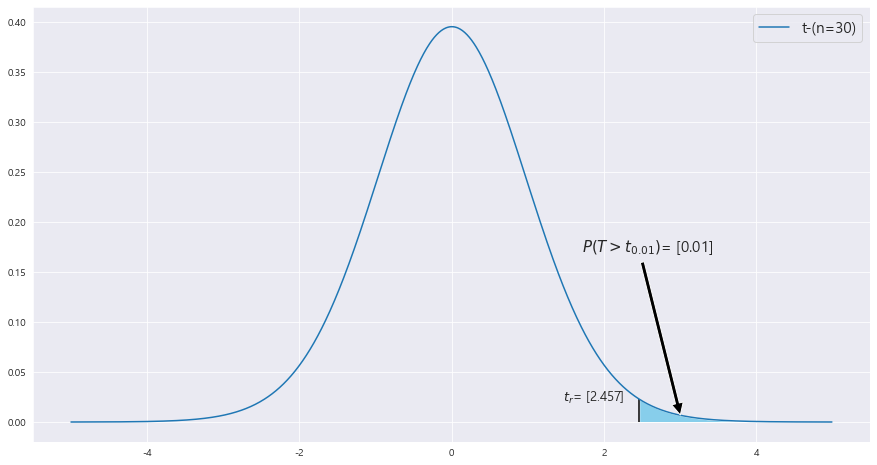
3> 모분산_A = 모분산_B = 33, P(S_p**2 > s_0) = 0.01을 만족하는 s_0을 구하라.
모분산을 알때는?! ==> 카이제곱분포!

V = (n+m-2) * S_p**2 / 모분산
n = 32
dof = 30
P( 30 * S_p**2 /33 > 30*s_0 / 33) = P(T> 30*s_0/33) = 0.01
31*s_0/33 = 50.89
s_0 = 55.979
x = np.arange(0 , 100 , .01)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , scipy.stats.chi2(dof).pdf(x)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
dof = 30
X_r = scipy.stats.chi2(dof).ppf(1- 0.01)
# X_r = 18.49
print(X_r)
ax.fill_between(x, scipy.stats.chi2(dof).pdf(x) , where = (x>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = 1- scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(52 , .015, 'P(X >' + r'$\chi^2_{0.01})$' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(55, .001), xytext=(54 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 15, .003, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
plt.annotate('' , xy=(50, .001), xytext=(40 , .001) , arrowprops = dict(facecolor = 'black'))
b = [r'$\chi^2(\eta$ = {})'.format(dof)]
print(b)
plt.legend(b , fontsize = 15)
t = Symbol('t')
c = solve(33*50.89/30 -t)
print(c)
4> 모분산_A = 30 , 모분산_B = 35일때 , P(S_1**2 / S_2**2 > f_0) = 0.05를 만족하는 f_0를 구하라.

(S_1**2 / 30) / (S_2**2 / 35) ~ F(15 , 15)
P( (S_1**2 / 30) / (S_2**2 / 35) > f_0*35/30) = 0.05
P(F > f_0*(35/30) ) = P(F>2.4) = 0.05
f_0 = 2.057
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★표본비율차이에 따른 표준정규분포★기초통계학-[연습문제02 -21] (0) | 2023.01.11 |
|---|---|
| ★표본평균의 차에 대한 절대값 처리★두 표본평균의 차에 따른 표준정규분포★기초통계학-[연습문제02 -19] (0) | 2023.01.11 |
| ★표본비율의 표본분포에 대한 정규분포 근사★표본비율★N(모평균 , 모평균*(1-모평균) / 전체표본개수★기초통계학-[연습문제02 -18] (1) | 2023.01.11 |
| ★모평균을 알때는 카이제곱★중심극한정리(표본평균의 표준정규분포)★이항분포의 평균,분산★기초통계학-[연습문제02 -17] (1) | 2023.01.10 |
| ★모분산을 모를때는 t-분포★기초통계학-[연습문제02 -16] (0) | 2023.01.09 |
★표본평균의 차에 대한 절대값 처리★두 표본평균의 차에 따른 표준정규분포★기초통계학-[연습문제02 -19]
25. 모평균과 모분산이 각각 뮤_1 = 178 , 뮤_2 = 166 , 모분산_1 = 16, 모분산_2 = 9이고 독립인 두 정규모집단에서 각각 크기 n=m = 16인 표본을 임의로 추출
https://knowallworld.tistory.com/307
★두 표본평균의 차에 대한 표본분포(모분산 알때 , 동일할때)★중심극한정리 활용★이표본의
1. 이표본의 표본분포 ==>지금까지는 단일 모집단의 표본에 대한 통계량의 표본분포 EX) 수능에서 남학생, 여학생 집단의 평균이 동일한지 여부 비교 ==> 비교위해서는 각각 표본을 추출하여야 한
knowallworld.tistory.com

1> 두 표본평균 차에 대한 확률 분포
|X - |Y ~ N(178-166 , 1+ 9/16)
2> 두 표본평균의 차가 10 이상일 확률
P(|X-|Y >= 10) = P(Z>= (10-12) / 루트(16+81/16) ) = P(-1.41<=Z) = 0.9207
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((10 - 12) / math.sqrt(1 + 9/16) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
# z_1 = round(scipy.stats.norm.ppf(1- 0.025) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- scipy.stats.norm.cdf(z_1)
ax.text(2 , .12, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.3, .012), xytext=(3 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
26. 여자 평균 79점, 표준편차 15점, 남학생은 77점, 표준편차 10점 , 여학생 40명 , 남학생 50명 임의 선정
뮤_|x = 79
s_|x = 15
n = 40
뮤_|y = 77
s_|y = 10
m = 50
1> 표본으로 선정된 여학생과 남학생의 평균점수의 차에 대한 확률분포
|X-|Y ~ N(79-77 , 15**2 /40 + 10**2/50)
2> 여학생의 평균이 남학생의 평균보다 1점 이상일 확률
P(|X-|Y >= 1) = P(Z >= 1-2 / 루트(15**2 /40 + 10**2/50) ) = P(-0.36<=Z) = 0.6406
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((1 - 2) / math.sqrt(15**2 / 40 + 10**2 / 50) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
# z_1 = round(scipy.stats.norm.ppf(1- 0.025) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- scipy.stats.norm.cdf(z_1)
ax.text(2 , .12, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.3, .012), xytext=(3 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))

27. 평균 근속연수 남녀간 차이 6년 , 두 그룹의 표준편차가 동일하게 3년 , 남자 직원 250명, 여자 직원 200명 임의 선정
1> 표본으로 선정된 남녀 직원의 평균 근속 연수의 차에 대한 확률분포
| |X-|Y | ~ N(6 , 9/250 + 9/200)
2> 남자와 여자의 평균 근속 연수의 차가 +- 5년 사이일 확률( 다시 풀자)
P( | |X - |Y | <5 ) = P( |Z| < 5-6 / 루트(9/250 + 9/200) ) = P( |Z| < 3.51) = [ P(Z<3.51) - P(Z<0) ] *2 =
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
# z_1 = round((-5-6) / math.sqrt(9/250 + 9/200 ) ,2)
z_1 = round((5-6) / math.sqrt(9/250 + 9/200) , 2)
print(z_1)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) & (x<=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((-z_1)) - scipy.stats.norm.cdf(0)) *2
ax.text(1.71 , .17, f'P({z_1}<=Z<={-z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
28. 남자 평균 연봉 8600만원 , 여자 평균 연봉 5800만원 , 표준편차가 동일하게 1000만원 , 남 직원 25명 , 여자 직원 20명
1> 표본으로 선정된 남자 직원과 여자 직원의 평균연봉의 차에 대한 학률분포
|X-|Y ~ N(2800 , 1000**2 / 25 + 1000**2 / 20)
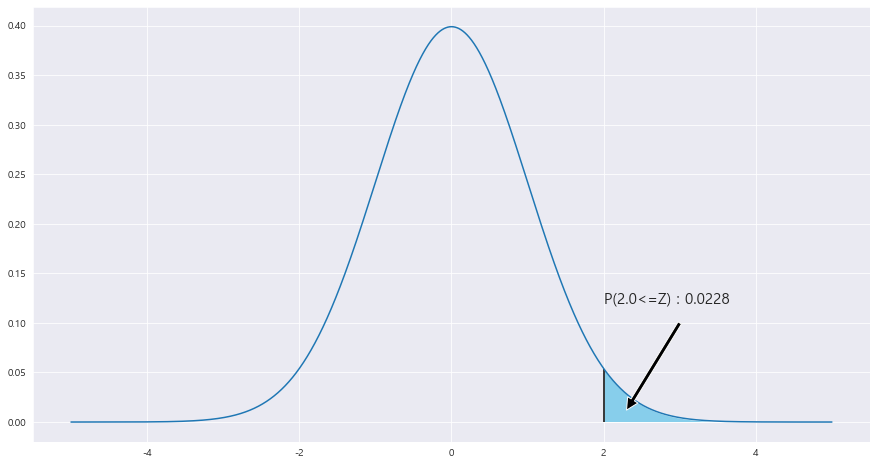
2> 남자 직원의 평균 연봉이 여자 직원의 평균 연봉보다 3400만원 이상 높을 확률
P(|X-|Y >= 3400) = P(Z>= (3400-2800) / 루트(1000**2 / 25 + 1000**2 / 20) ) = 1 - P(Z<= (3400-2800) / 루트(1000**2 / 25 + 1000**2 / 20) ) = P(2<=Z) = 0.0228
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((3400 - 2800) / math.sqrt(1000**2 / 25 + 1000**2 / 20) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
# z_1 = round(scipy.stats.norm.ppf(1- 0.025) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- scipy.stats.norm.cdf(z_1)
ax.text(2 , .12, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.3, .012), xytext=(3 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★표본비율차이에 따른 표준정규분포★기초통계학-[연습문제02 -21] (0) | 2023.01.11 |
|---|---|
| ★종합선물세트★F-분포(표본분산의 비 이용!)★표본평균의 차에 따른 확률분포!★합동표본분산 구하는 법!★모분산을 모를땐 t-분포★모분산을 알때는 카이제곱분포★기초통계학-[연습문제.. (0) | 2023.01.11 |
| ★표본비율의 표본분포에 대한 정규분포 근사★표본비율★N(모평균 , 모평균*(1-모평균) / 전체표본개수★기초통계학-[연습문제02 -18] (1) | 2023.01.11 |
| ★모평균을 알때는 카이제곱★중심극한정리(표본평균의 표준정규분포)★이항분포의 평균,분산★기초통계학-[연습문제02 -17] (1) | 2023.01.10 |
| ★모분산을 모를때는 t-분포★기초통계학-[연습문제02 -16] (0) | 2023.01.09 |