★종합선물세트★F-분포(표본분산의 비 이용!)★표본평균의 차에 따른 확률분포!★합동표본분산 구하는 법!★모분산을 모를땐 t-분포★모분산을 알때는 카이제곱분포★기초통계학-[연습문제..
29. 두 정규모집단 A와 B의 모분산은 동일하고, 평균은 각각 뮤_1 = 700 , 뮤_2 = 680이라 한다. 두 모집단으로 부터 표본을 추출하여 A 표본 [n = 17 , |x = 704 , s_1 = 39.25] , B표본 [m = 10 , |y = 675 , s_2 = 43.75]
https://knowallworld.tistory.com/309
★서로독립인 정규집단의 표본분산(모분산은 알때) 추론★카이제곱분포★합동표본분산에 대한
1. 합동표본분산에 대한 표본분포 ==> 동일한 모분산을 갖는 서로 독립인 두 정규 모집단 ==> 크기가 n과 m인 두 확률표본 추출 ==>두 표본의 표본분산에 대한 합동표본분산 정의 https://knowallworld.tist
knowallworld.tistory.com
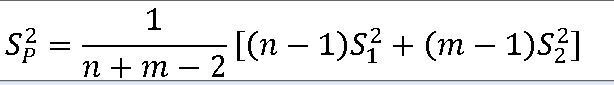
https://knowallworld.tistory.com/308
★두 표본평균의 차에 대한 표본분포(모분산 모를때)★중심극한정리 활용★이표본의 표본분포
1. 두 표본평균의 차에 대한 표본분포(두 모분산을 모르는 경우) https://knowallworld.tistory.com/302 ★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본 1. 표
knowallworld.tistory.com
1> 두 표본에 대한 합동표본분산 s_p**2을 구하라.
s_p**2 = 1/(17+10-2) * (16*(39.25**2) + 9*(43.75**2) ) = 1675.0225
2> 두 표본평균의 차 T = |X - |Y 에 대한 확률분포를 구하라.
https://knowallworld.tistory.com/307
★두 표본평균의 차에 대한 표본분포(모분산 알때 , 동일할때)★중심극한정리 활용★이표본의
1. 이표본의 표본분포 ==>지금까지는 단일 모집단의 표본에 대한 통계량의 표본분포 EX) 수능에서 남학생, 여학생 집단의 평균이 동일한지 여부 비교 ==> 비교위해서는 각각 표본을 추출하여야 한
knowallworld.tistory.com
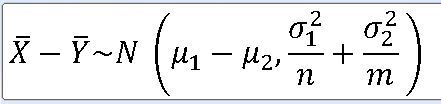
|X의 평균 = 704
분산 = 39.25**2
N = 17
|Y의 평균 = 675
분산 = 43.75**2
M = 10
모평균_|X-모평균_|Y = 20
s_|x-|y = 루트(1675.0225) * (루트(1/17 + 1/10) )
(T-20) / (루트(1675.0225) * (루트(1/17 + 1/10) ) ~ T(25)
https://knowallworld.tistory.com/259
★scipy.stats.t(자유도).ppf()★t-분포★기초통계학-[Chapter06 - 연속확률분포-07]
1. T-분포(Chi-square Distribution) ==> T-분포는 모분산이 알려지지 않은 정규모집단의 모평균에 대한 추론 ==>서로 독립인 표준정규화확률변수 Z와 자유도 n인 카이제곱 확률변수 V에 대하여 정의 ==> T ~
knowallworld.tistory.com
==> 모분산을 모를땐 t-분포! , 알때는 카이제곱분포(표본분산 추정)
==> χ²분포는 정규분포를 따르는 변수의 분산을 분석할 때 사용
==>T분포는 모분산을 모르는 경우에 표본분산을 이용해서 분석할 때 사용
3> P(T>t_0) = 0.05인 t_0를 구하라.
X = np.arange(-5,5 , .01)
fig = plt.figure(figsize=(15,8))
dof_2 = [25] #자유도
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
t_r = scipy.stats.t(dof_2).ppf(1- 0.05)
print(t_r)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
plt.annotate('' , xy=(3.0, .007), xytext=(2.5 , .16) , arrowprops = dict(facecolor = 'black'))
ax.text(1.71 , .17, r'$P(T>t_{0.05})$' + f'= {0.05}',fontsize=15)
ax.text(t_r - 1 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
t = Symbol('t')
a = solve( (t - 20)/ (math.sqrt(1675.0225)* math.sqrt(1/17 + 1/10)) - 1.708)
print(a)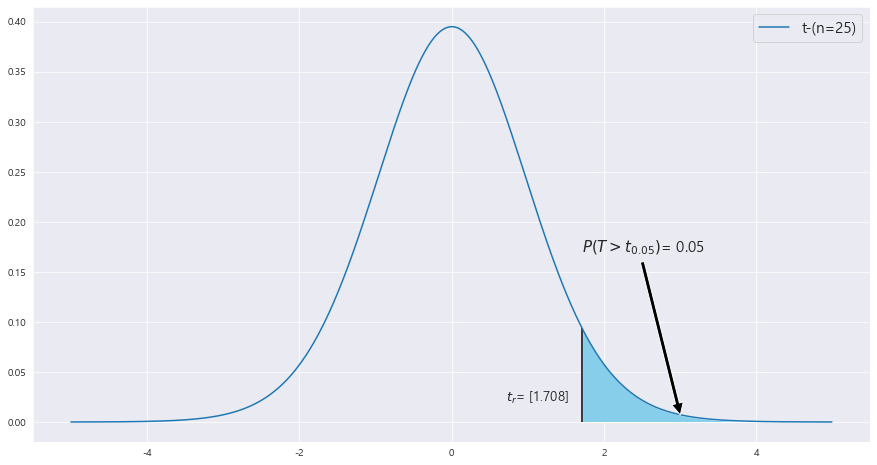
30. 환자 32명을 두 그룹으로 분할, 평균수치가 높을수록 치료의 효과가 있다. 치료법 A = [n=14 , |x = 47.20 , s_2**2 = 111.234] , 치료법 B = [m = 18 , |y = 43.43 , s_1**2 = 105.252]
1> 두표본에 대한 합동표본분산을 구하라.
s_p**2 = (1/ n+m-2) * ( (n-1)*s_1**2 + (m-1)*s_2**2 ) = (1/30) * (13*111.234 + 17*105.252) = 107.8442
2> 뮤_1 = 뮤_2 라 할 때 , 이 표본에 기초하여 P(|X - |Y > 10.175)를 구하라.
|X의 평균 = 47.20
n = 14
s_2 = 루트(111.234)
|Y의 평균 = 43.43
m = 18
s_1 = 루트(105.252)
자유도 = 32 - 2 = 30
모평균_|x - 모평균_y = 0(모평균이 같다!)
분산_|X-|Y = 루트(107.8442) * 루트(1/14 + 1/18)
t_r = round( (10.715 - (0)) / (math.sqrt(107.8442) * math.sqrt(1/14 + 1/18)), 3)P(T > [10.715 - (0)] / 분산_|X-|Y) = P(T> t_0.004) = P(T>2.895) = 0.004
X = np.arange(-5,5 , .01)
fig = plt.figure(figsize=(15,8))
dof_2 = [30] #자유도
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
# t_r = scipy.stats.t(dof_2).cdf(1- 0.05)
t_r = round( (10.715 - (0)) / (math.sqrt(107.8442) * math.sqrt(1/14 + 1/18)), 3)
print(t_r)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
plt.annotate('' , xy=(3.0, .007), xytext=(2.5 , .16) , arrowprops = dict(facecolor = 'black'))
area = 1- scipy.stats.t(dof_2).cdf(t_r)
ax.text(1.71 , .17, r'$P(T>t_{0.004})$' + f'= {area}',fontsize=15)
ax.text(t_r - 1 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
3> 모분산_|x = 모분산_|y = 102일때, 합동표본분산이 62.87보다 클 확률
|X의 평균 = 47.20
n = 14
s_2 = 루트(111.234)
|Y의 평균 = 43.43
m = 18
s_1 = 루트(105.252)
자유도 = 32 - 2 = 30
==>모분산 안다?! ==> 카이제곱 분포
https://knowallworld.tistory.com/309
★서로독립인 정규집단의 표본분산(모분산은 알때) 추론★카이제곱분포★합동표본분산에 대한
1. 합동표본분산에 대한 표본분포 ==> 동일한 모분산을 갖는 서로 독립인 두 정규 모집단 ==> 크기가 n과 m인 두 확률표본 추출 ==>두 표본의 표본분산에 대한 합동표본분산 정의 https://knowallworld.tist
knowallworld.tistory.com

V = (n-1)*s_p**2 / 모분산
x = 30/102* S_p**2 ~ X**2(30)
P(S**2 > 62.87) = P(30/102*S**2 > 30 * 62.87 / 102) = P(X>= 18.49) = 0.95
4> 모분산_|x = 모분산_|y = 102일때, P(S_1**2 > 0.4*S_2**2) 를 구하라.(답지가 이상하다?!)
|X의 평균 = 47.20
n = 14
s_2 = 루트(111.234)
|Y의 평균 = 43.43
m = 18
s_1 = 루트(105.252)
https://knowallworld.tistory.com/310
★F-분포★두 표본분산의 비에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -11]
1. 두 표본분산의 비에 대한 표본분포 ==> 서로 독립인 두 정규모집단의 모분산이 다를때, 모분산 중에서 어느 것이 더큰지 비교하는 경우 ==> 모분산은 양수이므로, 두 모분산의 비의 값을 이용하
knowallworld.tistory.com
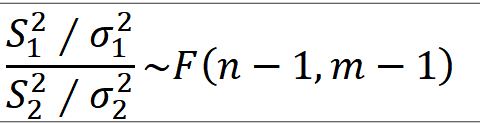
==> 서로 독립인 두 모집단의 모분산이 동일한지 아닌지를 통계적으로 추론
==> 모분산 동일하지 않을 때 표본분포 값 구한다.
(S_1**2 / 모분산_1) / (S_2**2/ 모분산_2) = (S_1**2) / (S_2**2) ~ F(13,17)
P(S_1**2 > 0.4*S_2**2) = P(S_1**2 / S_2**2 > 0.4) = P(F>0.4) = 0.95(답지가 이상)
X = np.arange(0,10, .01)
fig = plt.figure(figsize = (15,8))
dof = [[13,17]]
#print(dof[0][0])
for i in dof:
ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
b = ['F({},{})'.format(i,j) for i,j in dof]
X_r = 0.4
print(X_r)
# X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(0.04)
# ax.fill_between(X, scipy.stats.f(dof[0][0],dof[0][1]).pdf(X) , where = (X>=X_r) | (X<=X_l) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
ax.fill_between(X, scipy.stats.f(dof[0][0],dof[0][1]).pdf(X) , where = (X>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
ax.vlines(X_r , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_r) , color = 'black')
# ax.vlines(X_l , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_l) , color = 'black')
area = round(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_r) ,2 )
# ax.annotate('' , xy=(X_l -0.02 , 0.1) , xytext=(X_l + 0.5 , 0.1) , arrowprops = dict(facecolor = 'black'))
# ax.text(X_l + 0.5 , 0.1 , r'$P(F\leqq f_{0.95,4,5})$' + f'= {0.05}' , fontsize = 14)
ax.annotate('' , xy=(X_r +0.3 , 0.01) , xytext=(X_r + 0.3 , 0.2) , arrowprops = dict(facecolor = 'black'))
ax.text(X_r + 0.3 , 0.21 , r'$P(F\geqq f_{0.95,13,17}$' + f'= {area}' , fontsize = 14)
# ax.text(X_l + 0.05 , 0.01 , r'$f_{0.95,4,5}$)' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(0.05) ,2)}' ,fontsize = 13)
ax.text(X_r - 1.3 , 0.01 , r'$f_{0.95,13,17}$' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- area) , 2)}' ,fontsize = 13)
plt.legend(b , fontsize= 15)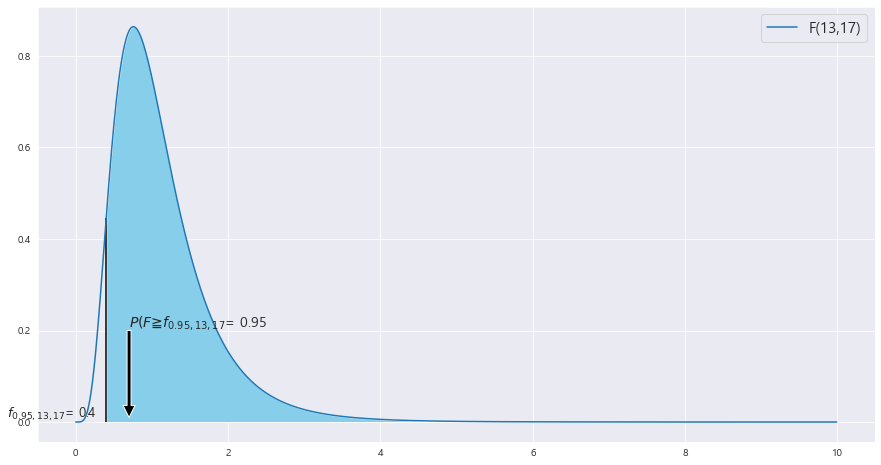
31. 시중에서 판매되고 있는 두 회사의 커피믹스에 포함된 카페인의 양을 조사, 제조된 커피믹스에 포함된 카페인의 양은 동일한 분산을 갖는 정규분포 A= [n = 16 , |x = 78 , s_1**2 = 32.5] , B = [m =16 , |y = 75 , s_2**2 = 34.2]
1> 두 표본에 대한 합동표본분산
s_p**2 = (1/ n+m-2) * ( (n-1)*s_1**2 + (m-1)*s_2**2 ) = (1/30) * (15*32.5 + 15*34.2) = 33.35
2> 모평균_A = 모평균_B 일 때 , P(|X-|Y > x_0 ) = 0.01을 만족하는 x_0을 구하라.
모분산 모른다! ==> t-분포 활용
모평균_A - 모평균_B = 0
(T - 0) / (루트(33.35) * 루트(1/16 + 1/16) ) ~ t(30)
P(T > x_0/(루트(33.35) * 루트(1/16 + 1/16) ) ) = 0.01
P(T>2.457) = 0.01
x_0 / (루트(33.35) * 루트(1/16 + 1/16) ) = 2.457
x_0 = 5.016
X = np.arange(-5,5 , .01)
fig = plt.figure(figsize=(15,8))
dof_2 = [30] #자유도
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
t_r = scipy.stats.t(dof_2).ppf(1-0.01)
# t_r = round( (x_0 - (0)) / (math.sqrt(33.463) * math.sqrt(1/16 + 1/16)), 3)
print(t_r)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
plt.annotate('' , xy=(3.0, .007), xytext=(2.5 , .16) , arrowprops = dict(facecolor = 'black'))
area = 1- scipy.stats.t(dof_2).cdf(t_r)
ax.text(1.71 , .17, r'$P(T>t_{0.01})$' + f'= {area}',fontsize=15)
ax.text(t_r - 1 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
t = Symbol('t')
a = solve( t- 2.457 * (math.sqrt(33.35)* math.sqrt(1/16 + 1/16)))
print((math.sqrt(33.35)* math.sqrt(1/16 + 1/16)))
print(a)
3> 모분산_A = 모분산_B = 33, P(S_p**2 > s_0) = 0.01을 만족하는 s_0을 구하라.
모분산을 알때는?! ==> 카이제곱분포!

V = (n+m-2) * S_p**2 / 모분산
n = 32
dof = 30
P( 30 * S_p**2 /33 > 30*s_0 / 33) = P(T> 30*s_0/33) = 0.01
31*s_0/33 = 50.89
s_0 = 55.979
x = np.arange(0 , 100 , .01)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , scipy.stats.chi2(dof).pdf(x)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
dof = 30
X_r = scipy.stats.chi2(dof).ppf(1- 0.01)
# X_r = 18.49
print(X_r)
ax.fill_between(x, scipy.stats.chi2(dof).pdf(x) , where = (x>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = 1- scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(52 , .015, 'P(X >' + r'$\chi^2_{0.01})$' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(55, .001), xytext=(54 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 15, .003, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
plt.annotate('' , xy=(50, .001), xytext=(40 , .001) , arrowprops = dict(facecolor = 'black'))
b = [r'$\chi^2(\eta$ = {})'.format(dof)]
print(b)
plt.legend(b , fontsize = 15)
t = Symbol('t')
c = solve(33*50.89/30 -t)
print(c)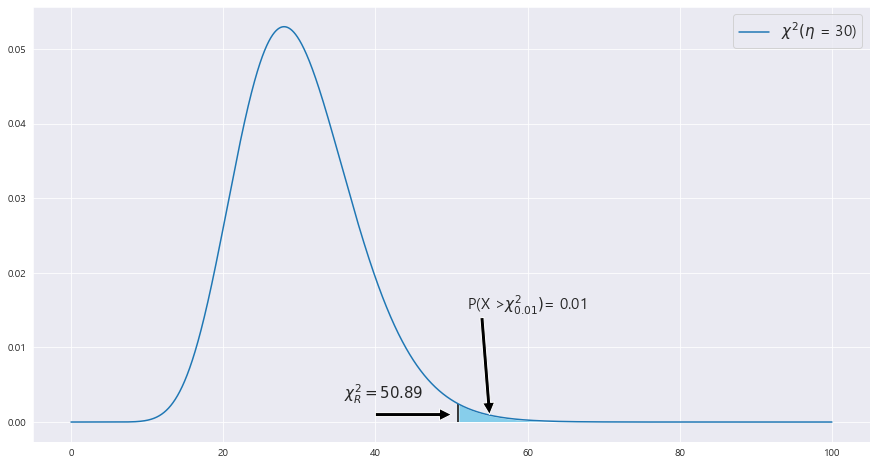
4> 모분산_A = 30 , 모분산_B = 35일때 , P(S_1**2 / S_2**2 > f_0) = 0.05를 만족하는 f_0를 구하라.
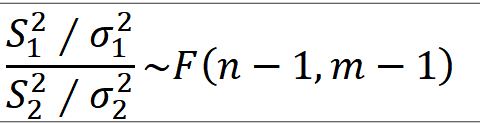
(S_1**2 / 30) / (S_2**2 / 35) ~ F(15 , 15)
P( (S_1**2 / 30) / (S_2**2 / 35) > f_0*35/30) = 0.05
P(F > f_0*(35/30) ) = P(F>2.4) = 0.05
f_0 = 2.057
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★표본비율차이에 따른 표준정규분포★기초통계학-[연습문제02 -21] (0) | 2023.01.11 |
|---|---|
| ★표본평균의 차에 대한 절대값 처리★두 표본평균의 차에 따른 표준정규분포★기초통계학-[연습문제02 -19] (0) | 2023.01.11 |
| ★표본비율의 표본분포에 대한 정규분포 근사★표본비율★N(모평균 , 모평균*(1-모평균) / 전체표본개수★기초통계학-[연습문제02 -18] (1) | 2023.01.11 |
| ★모평균을 알때는 카이제곱★중심극한정리(표본평균의 표준정규분포)★이항분포의 평균,분산★기초통계학-[연습문제02 -17] (1) | 2023.01.10 |
| ★모분산을 모를때는 t-분포★기초통계학-[연습문제02 -16] (0) | 2023.01.09 |