★불편추정량★최소분산불편추정량★유효 추정량★불편 추정량★기초통계학-[대표본 추정 -02]
1. 유효추정량
==> 일반적으로 절사평균은 모평균에 대한 불편추정량이 아니다.
https://knowallworld.tistory.com/213
np.median★절사평균, 중위수★기초통계학-[Chapter03 - 03]
1. 절사평균 A = [1,2,3,4,5] 의 산술평균 : 3 B = [1,2,3,4,50]의 산술평균 : 12 ==> 산술평균은 특이점(_50_) 과 같이 유무에 따라 많은 영향을 받는다. ==> 특이점 있을경우 특이점 제거한다면 특이점의 영향
knowallworld.tistory.com
==> 절사평균은 특이점을 제거한 평균 사용 ==> 보편적으로 양쪽 끝 5%~10% 절사
==> 표본 중위수도 모집단 중위수에 대한 불편추정량이 되지 못한다.
https://knowallworld.tistory.com/211
★모평균, 표본평균★중심위치의 척도★기초통계학-[Chapter03 - 01]
1. 중심위치의 척도 ==> 원자료를 의미 있는 형태로 정리하기 위해 도수분포표를 작성하여 결과를 히스토그램 또는 도수다각형의 그림으로 나타냄 ==> 자료가 집중하는 경향을 수치로 나타내는
knowallworld.tistory.com
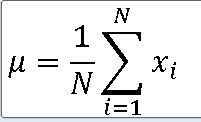
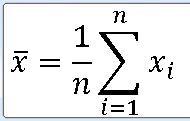
표본평균 |X = 모평균 M
==> 모평균 M에 대한 불편추정량
https://knowallworld.tistory.com/305
★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집
1. 모분산의 표본분포 정규모집단 N(뮤 , 모분산) 으로부터 크기 n인 표본을 선정할 때 표본분산 ==> 표본분산 S**2에 대한 표본분포는 X**2-통계량 V에 대하여 자유도가 n-1인 카이제곱분포이다. https:
knowallworld.tistory.com
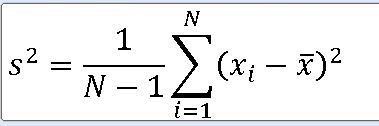
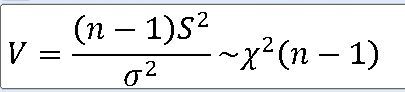
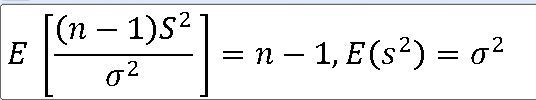
표본분산 s**2 은 모분산에 대한 불편 추정량
https://knowallworld.tistory.com/306
이항분포에 따른 정규분포의 표준정규분포화★표본비율의 표본분포★기초통계학-[모집단 분포
1.표본비율의 표본분포 EX) 이항 확률변수의 실질적인 응용 ==> 여론조사 생각 ==> 모집단을 구성하는 사람들의 어느 특정 사건을 선호하는 비율(p)를 알기 위하여 n명으로 구성된 표본을 임의 선정
knowallworld.tistory.com
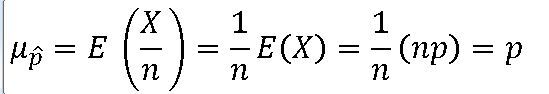
==> 표본비율은 모비율 p에 대한 불편추정량
WHY 표본분산을 정의 할때 n-1을 하는가!!!
E(S**2) = (n-1)/ n * 모분산 != 모분산
==> 크기 n-1로 나누어야 불편성을 갖으므로 표본분산을 정의 할때 n-1로 나누어 정의한다.
유효추정량 : 추정량의 표본분포가 모수의 참값에 가장 가깝게 분포하는 경우, 즉 가장 작은 분산을 갖는 추정량이다.
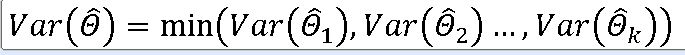
표준오차 : 모수를 추정하기 위해 사용되는 추정량의 표준편차
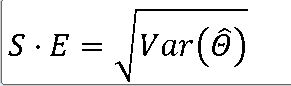
EX-01) 모평균이 M(뮤) 인 모집단에서 크기 3인 확률표본 {X_1 , X_2 , X_3}을 추출 , 모평균에 대한 불편추정량 중에서 유효성을 갖는 추정량
^M_1 = (1/3)* (X_1 + X_2 + X_3)
^M_2 = (1/4) * ( (2* X_1) + X_2 + X_3)
^M_3 = (1/5) * ( X_1 + (2* X_2) + (2* X_3 ) )
^M_4 = (1/5) * ( X_1 +(2* X_2 ) + X_3)
==> X_1, X_2 , X_3이 동일한 모집단 분포를 따르므로 Var(X_1) = Var(X_2) = Var(X_3)= 모분산
https://knowallworld.tistory.com/255
★정규분포의 표준정규분포로의 변환★추측통계학-[Chapter06 - 연속확률분포-04]
1. 확률변수 X와 Y에 대한 분산 2. 서로 독립인 확률변수 X와 Y가 정규분포 X ~N(뮤_1 , 분산) , Y~ N(뮤_2 , 분산) 따르는 경우의 추측통계학 EX-01) X는 N(1995 , 144) Y는 N(1755 , 100) 1> X-Y의 확률분포 X-Y ~ N(1995
knowallworld.tistory.com
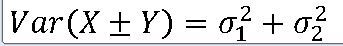
Var(^M_1) = (1/9)* Var(X_1 + X_2 + X_3) = (1/9) * (모분산 + 모분산 + 모분산) = (1/3) * 모분산
Var(^M_2) = (1/16) * Var(2*X_1 + X_2 + X_3) = (1/16) * Var(4*모분산 + 모분산 + 모분산) = (3/8)*모분산
Var(^M_3) = (1/25) * Var(X_1 + 2*X_2 + 2*X_3 ) = (1/25) * Var(모분산 + 4*모분산 + 4*모분산) = (9/25) * 모분산
Var(^M_2) > Var(^M_3) > Var(^M_1)
==> 유효추정량은 Var(^M_1) 이다.
EX-02) 모평균이 M(뮤) 인 모집단에서 크기 2인 확률표본 {X_1 , X_2}을 추출 , 모평균에 대한 불편추정량 중에서 유효성을 갖는 추정량
^M_1 = X_1
^M_2 = (1/2) * (X_1 +X_2)
^M_3 = (1/2) * (X_1 + 2*X_2)
^M_4 = (1/3) * (X_1 + 2*X_2)
==> ^M_1 , ^M_2 , ^M_4 ==> 불편추정량
Var(^M_1) = Var(X_1) = 1*모분산
Var(^M_2) = (1/4)* Var(X_1 + X_2) = (1/4)* (Var(X_1) + Var(X_2) ) = (1/2) * 모분산
Var(^M_4) = (1/9) * Var(X_1 + 2*X_2) = (1/9) * ( Var(X_1) + 4Var(X_2) ) = (5/9)* 모분산
Var(^M_2) < Var(^M_3) < Var(^M_1)
==> Var(^M_2) 가 유효추정량
2. 최소분산불편추정량(Minimum Variance unbiased estimator)
==> 모두에 대한 불편성과 유효성을 모두 갖는 추정량이다.
x = np.arange(-1,1 ,.001)
fig = plt.figure(figsize= (15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale = math.sqrt(1/10))) #정의역 범위 , 표본평균의 평균 = 0 , 표본평균의 분산 =1/10 인 정규분포 플롯
plt.annotate('' , xy=(0.5, .5), xytext=(.75 , .5) , arrowprops = dict(facecolor = 'black'))
ax.text(0.75 , 0.5 , r'n = 10' , fontsize = 13)
sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale= math.sqrt(1/20))) #정의역 범위 , 표본평균의 평균 = 0 , 표본평균의 분산 =1/20 인 정규분포 플롯
plt.annotate('' , xy=(0.25, 1.1), xytext=(.4 , 1.5) , arrowprops = dict(facecolor = 'black'))
ax.text(0.4 , 1.5 , r'n = 20' , fontsize = 13)
sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =math.sqrt(1/50))) #정의역 범위 , 표본평균의 평균 = 0 , 표본평균의 분산 =1/50 인 정규분포 플롯
plt.annotate('' , xy=(-0.16, 1.5), xytext=(-.25 , 2) , arrowprops = dict(facecolor = 'black'))
ax.text(-0.35 , 2.1 , r'n = 50' , fontsize = 13)
sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =math.sqrt(1/100))) #정의역 범위 , 표본평균의 평균 = 0 , 표본평균의 분산 =1/100 인 정규분포 플롯
ax.axvline(x= 0, ymin=0 , ymax=1 , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
plt.annotate('' , xy=(-0.08, 3), xytext=(-.25 , 3) , arrowprops = dict(facecolor = 'black'))
ax.text(-0.35 , 3.1 , r'n = 100' , fontsize = 13)
ax.text(0, .41, f'평균 : {round(0,2)}',fontsize=13)
plt.legend(['N(0,1/10)' , 'N(0,1/20)' , 'N(0,1/50)' , 'N(0,1/100)' ] , fontsize = 15)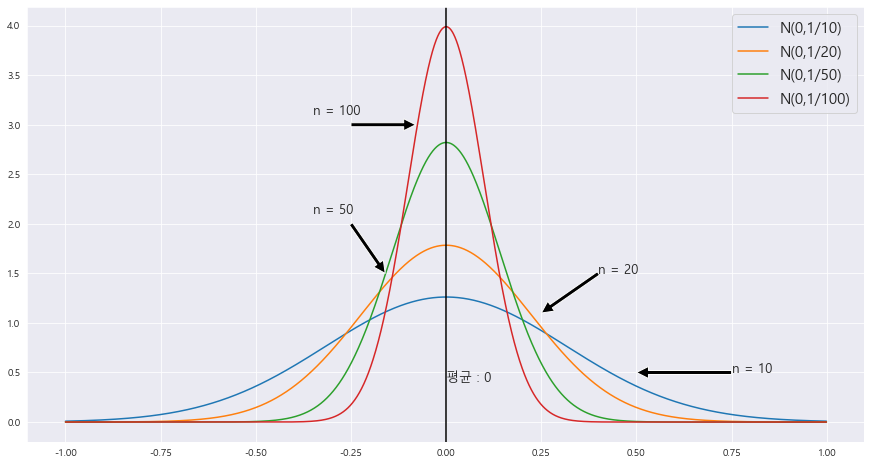
EX-01) 성인이 전자책에 있는 텍스트 한 쪽을 읽는 데 걸리는 평균 시간을 추정하기 위하여 다음과 같이 12명을 임의로 선정하여 시간을 측정하였다. 이때 텍스트 한 쪽을 읽는 데 걸리는 시간은 표준편차가 8초인 정규분포를 따른다고 알려졌다. 이 표본을 이용하여 성인이 텍스트 한 쪽을 읽는 데 걸리는 평균시간을 추정하고, 표준오차를 구하라.
A= [ 43.2 , 41.5 , 48.3 , 37.7 , 46.8 , 42.6 , 46.7, 51.4 , 47.3 , 40.1 , 46.2 , 44.7]
평균 _|A = 44.7083
A ~ N(44.7083 , 8/루트(12) )
s = 8
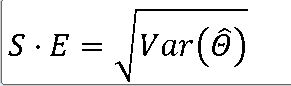
|X의 표준편차(오차) = 8 /루트(12) = 2.31
EX-02) 9명의 어린이가 하루 동안 TV를 시청하는 시간 A = [2.2 , 3.1 , 3.8 , 2.7 , 4.0 , 2.6 , 2.4 , 1.6 , 2.3] , 이 표본을 이용하여 하루동안 TV를 시청하는 평균 시간을 추정하고, 표준오차를 구하라.(분산이 0.5시간인 정규분포를 따른다.)
A ~ N(뮤 , 0.5)
==> |A가 모평균에 대한 최소분산불편추정량이므로 표본평균을 구할 수 있다.

|A ~ N(2.744 , 0.5/9)
A = [2.2 , 3.1 , 3.8 , 2.7 , 4.0 , 2.6 , 2.4 , 1.6 , 2.3]
MEANS = np.mean(A)
print(MEANS)
print(math.sqrt(0.5/9))시청 평균시간 = 2.744
|A의 표준편차 = 루트(0.5/9) = 0.2357
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 대표본 추정' 카테고리의 다른 글
| ★string r'로 받을때 안에 값 집어넣기(변수로도 %2d)★모비율 차의 구간추정★기초통계학-[대표본 추정 -06] (0) | 2023.01.11 |
|---|---|
| ★모평균 차의 구간추정★기초통계학-[대표본 추정 -05] (0) | 2023.01.11 |
| ★모비율의 신뢰구간★기초통계학-[대표본 추정 -04] (0) | 2023.01.11 |
| ★신뢰구간★신뢰도★구간추정★기초통계학-[대표본 추정 -03] (0) | 2023.01.11 |
| ★편의 추정량★불편 추정량★기초통계학-[대표본 추정 -01] (1) | 2023.01.11 |