np.median★절사평균, 중위수★기초통계학-[Chapter03 - 03]
1. 절사평균
A = [1,2,3,4,5] 의 산술평균 : 3
B = [1,2,3,4,50]의 산술평균 : 12
==> 산술평균은 특이점(_50_) 과 같이 유무에 따라 많은 영향을 받는다.
==> 특이점 있을경우 특이점 제거한다면 특이점의 영향을 감소시킬 수 있다.
==> 절사평균은 이런 특이점을 제거한 평균 사용
==> 보편적으로 양쪽 끝 5%~10% 절사
EX) 240,24,27,30,28,31,22,27,30,25,25,23 에 대한 평균과 10% 절사평균을 구하라.
A = [240,24,27,30,28,31,22,27,30,25,25,23]
A = sorted(A , reverse=False)
print(A)
print('산술평균 : {}'.format(round(sum(A) / len(A),2)))
i = int(len(A)*0.1)
j = int(len(A) - i)
print(i)
print(j)
B = A[i:j]
print(B)
print('절사평균 : {}'.format(round(sum(B) / len(B),2)))
2. 중위수(Median)
240,24,27,30,28,31,22,27,30,25,25,23
특이점 : 240 ==> 평균에 큰 차이를 보인다.
절사평균 : 27.0
==> 자료를 작은 수부터 크기순으로 나열하여 한가운데에 놓이는 수이다.


중위수의 위치는 자료 집단의 상대도수다각형의 왼쪽 넓이와 오른쪽 넓이가 동일하게 0.5가 되는 경계값이다.
중위수 특징:
1. 특이점에 대해 전혀 영향을 받지않는다.
2.한 방향으로 치우치고 , 다른 방향으로 긴 꼬리 모양을 갖는 분포를 갖는 경우 평균보다 좋은 중심위치
EX) 240,24,27,30,28,31,22,27,30,25,25,23의 중위수
print(np.median(A))==> 27.0
2. 최빈값(Sample mode)
==> 2 번이상 발생하는 자료 값 중에서 가장 많은 도수를 가지는 자료 값
==> 최빈값은 질적 자료와 양적자료 모두 사용 가능
EX) 240,24,27,30,28,31,22,27,30,25,25,23의 최빈값
from scipy.stats import mode
import collections
b = collections.Counter(A)
print(b)
print(b.keys())
print(b.values())
mode(A) #최빈값 다수일 경우 첫번째 값 반환==> Counter({25: 2, 27: 2, 30: 2, 22: 1, 23: 1, 24: 1, 28: 1, 31: 1, 240: 1})
==> dict_keys([22, 23, 24, 25, 27, 28, 30, 31, 240])
==> dict_values([1, 1, 1, 2, 2, 1, 2, 1, 1])
==> ModeResult(mode=array([25]), count=array([2]))
fig = plt.figure(figsize = (8,8))
ax = plt.plot(figsize= (8,8))
fig.set_facecolor('white')
ax = sns.barplot(x=list(b.keys()) , y = list(b.values()))
ax.set_title('숫자별 빈도수')
ax.set_xlabel('숫자들' , fontsize= 13)
ax.set_ylabel('빈도수' , rotation = 0, fontsize= 13)
print(list(b.values()))
for i,txt in enumerate(list(b.values())):
c = txt
if c == max(list(b.values())):
ax.text(i, c+0.04, str(txt)+'개' , ha='center' , color = 'red' , fontweight = 'bold' , fontsize=17)
#어디 막대, 막대기의 위쪽에
else:
ax.text(i, c+0.05, str(txt)+'개' , ha='center' , color = 'dimgray' , fontsize=13 , fontweight = 'bold')
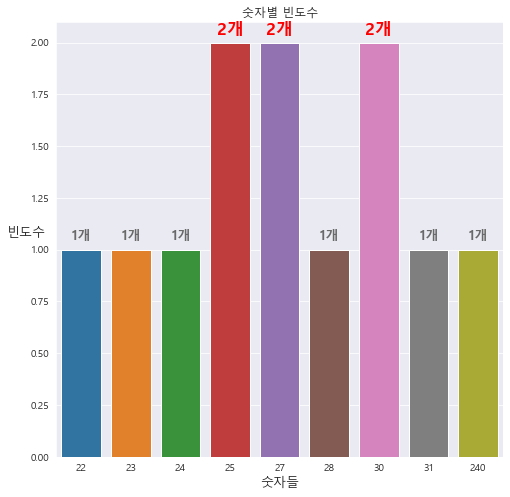
==> 쌍봉형 또는 여러 개의 봉우리 형태로 나타난다. ==> 쌍봉분포(bimodal distribution) or 다봉분포(Multimodal distribution)
==> 최빈값 1개 ==> 단봉분포(unimodal distribution)
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 평균,표준편차,분산' 카테고리의 다른 글
| 경험적규칙★체비쇼프 정리★기초통계학-[Chapter03 - 06] (0) | 2022.12.06 |
|---|---|
| ★distplot , histplot , twinx(), ticker , axvline()★정규분포 그래프★기초통계학-[Chapter03 - 05] (0) | 2022.12.06 |
| ★DDOF = 1★모/표본분산 , 모/표본표준편차★평균편차★기초통계학-[Chapter03 - 04] (0) | 2022.12.02 |
| ★가중평균, 표본평균★기초통계학-[Chapter03 - 02] (1) | 2022.12.02 |
| ★모평균, 표본평균★중심위치의 척도★기초통계학-[Chapter03 - 01] (0) | 2022.12.01 |