★F-분포★두 표본분산의 비에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -11]

1. 두 표본분산의 비에 대한 표본분포

 

==> 서로 독립인 두 정규모집단의 모분산이 다를때, 모분산 중에서 어느 것이 더큰지 비교하는 경우 

 

==> 모분산은 양수이므로, 두 모분산의 비의 값을 이용하여 비교가능

 

표본분산의 비

 

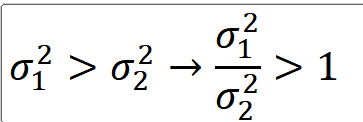
https://knowallworld.tistory.com/260

★scipy.stats.f(자유도1 , 자유도 2).pdf()★F-분포★기초통계학-[Chapter06 - 연속확률분포-08]

==> F-분포

 

==> 서로 독립인 두 모집단의 모분산이 동일한지 아닌지를 통계적으로 추론

 

==> 모분산 동일하지 않을 때 표본분포 값 구한다.

 

https://knowallworld.tistory.com/305

★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집

두 표본분산의 비의 표본분포는 F-분포

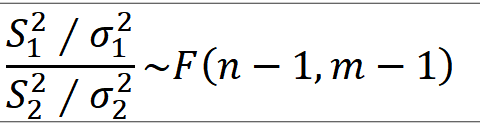
EX-01) 서로 독립인 두 정규모집단 N(뮤_1 , 9)와 N(뮤_2 , 8)에서 각각 크기 5와 6인 확률표본 추출, 이때

P( [S_1**2 / S_2**2] > s_0 ) = 0.05를 만족하는 s_0를 구하라.

 

n =  5

m = 6

 

자유도_1 = 5 -1 =4

자유도_2 = 6 -1  = 5

 

분산_1 = 9

분산_2 = 8

 

 

(S_1**2 / 9 ) / (S_2**2 / 8) ~ F(4,5)

X = np.arange(0,10, .01)

fig = plt.figure(figsize = (15,8))
dof = [[4,5]]
#print(dof[0][0])
for i in dof:
    ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
b = ['F({},{})'.format(i,j) for i,j in dof]


X_r = scipy.stats.f(dof[0][0], dof[0][1]).ppf(0.95)

X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(0.05)

ax.fill_between(X, scipy.stats.f(dof[0][0],dof[0][1]).pdf(X) , where = (X>=X_r) | (X<=X_l) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔


ax.vlines(X_r , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_r) , color = 'black')
ax.vlines(X_l , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_l) , color = 'black')


ax.annotate('' , xy=(X_l -0.02 , 0.1) , xytext=(X_l + 0.5 , 0.1) , arrowprops = dict(facecolor = 'black'))
ax.text(X_l + 0.5 , 0.1 , r'$P(F\leqq f_{0.95,4,5})$' + f'= {0.05}' , fontsize = 14)

ax.annotate('' , xy=(X_r +0.3 , 0.01) , xytext=(X_r + 0.3 , 0.2) , arrowprops = dict(facecolor = 'black'))
ax.text(X_r + 0.3 , 0.21 , r'$P(F\geqq f_{0.05,4,5})$' + f'= {0.05}' , fontsize = 14)

ax.text(X_l + 0.05 , 0.01 , r'$f_{0.95,4,5}$)' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(0.05) ,2)}' ,fontsize = 13)
ax.text(X_r - 1.3 , 0.01 , r'$f_{0.05,4,5}$)' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(0.95) , 2)}' ,fontsize = 13)


plt.legend(b , fontsize= 15)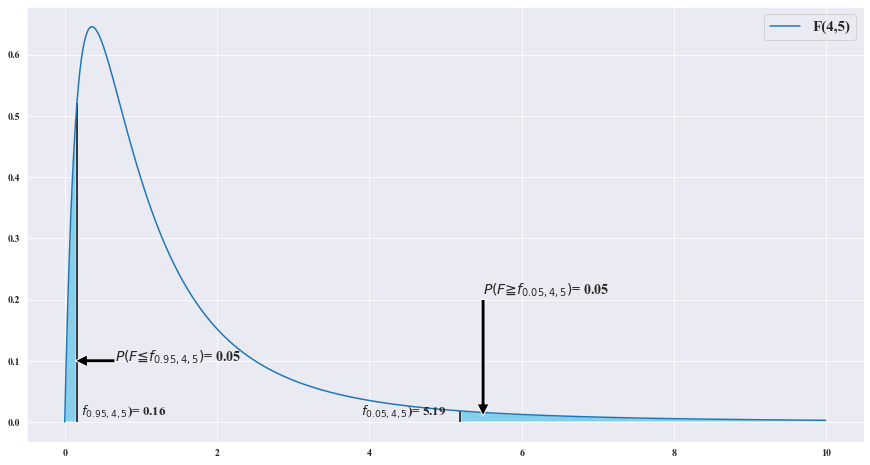

합동표본분산의 F-분포

 

P(S_1**2 / S_2**2 > s_0 ) = P( [8 * S_1**2] / [9  *S_2**2] > (8/9)*s_0 ) = P(F > (8/9)*s_0 ) = 0.05

 

s_0 = 5.19* (9/8) = 5.838

 

 

EX-02) 동일한 모분산을 갖는 서로 독립인 두 정규모집단에서 각각 크기 10과 15인 확률표본 추출, 이때

P( [S_1**2 / S_2**2] > s_0 ) = 0.025를 만족하는 s_0를 구하라.

 

모분산_1 = 모분산_2

 

n = 10

m = 15

 

자유도_1 = 10-1 = 9

자유도_2 = 15-1 = 14

 

P(F > s_0) = 0.025

 

X = np.arange(0,10, .01)

fig = plt.figure(figsize = (15,8))
dof = [[9,14]]
#print(dof[0][0])
for i in dof:
    ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
b = ['F({},{})'.format(i,j) for i,j in dof]


X_r = scipy.stats.f(dof[0][0], dof[0][1]).ppf(1-0.025)

X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(0.025)

ax.fill_between(X, scipy.stats.f(dof[0][0],dof[0][1]).pdf(X) , where = (X>=X_r) | (X<=X_l) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔


ax.vlines(X_r , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_r) , color = 'black')
ax.vlines(X_l , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_l) , color = 'black')


ax.annotate('' , xy=(X_l -0.02 , 0.1) , xytext=(X_l + 0.5 , 0.1) , arrowprops = dict(facecolor = 'black'))
ax.text(X_l + 0.5 , 0.1 , r'$P(F\leqq f_{0.975,9,14})$' + f'= {0.025}' , fontsize = 14)

ax.annotate('' , xy=(X_r +0.3 , 0.01) , xytext=(X_r + 0.3 , 0.2) , arrowprops = dict(facecolor = 'black'))
ax.text(X_r + 0.3 , 0.21 , r'$P(F\geqq f_{0.025,9,14})$' + f'= {0.025}' , fontsize = 14)

ax.text(X_l + 0.05 , 0.01 , r'$f_{0.975,9,14}$' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(X_l) ,2)}' ,fontsize = 13)
ax.text(X_r - 1.3 , 0.01 , r'$f_{0.025,9,14}$' + f'= {round(X_r , 2)}' ,fontsize = 13)


plt.legend(b , fontsize= 15)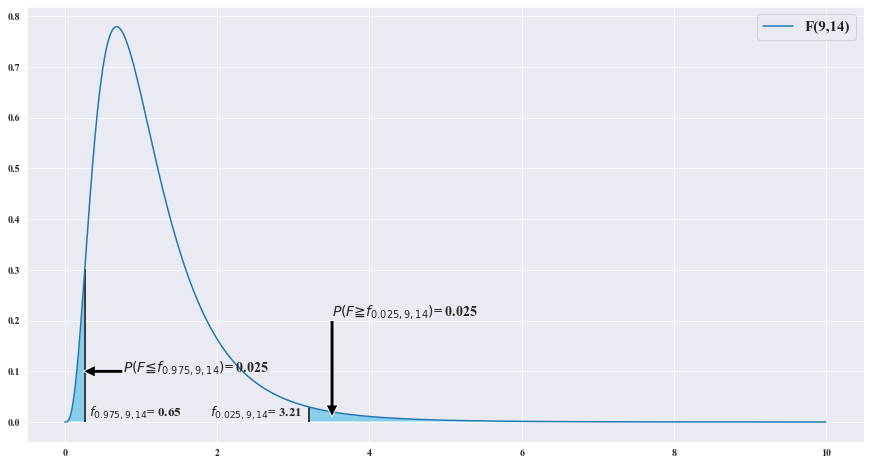

합동표본분포의 비에따른 F-분포

s_0 = 3.21

 

출처 :  [쉽게 배우는 생활속의 통계학]  [북스힐 , 이재원] 

※혼자 공부 정리용