★모평균의 차에 대한 신뢰구간★모비율에 대한 표본크기 구하기★표본의 크기★기초통계학-[대표본 추정 -06]
1. 표본의 크기
==> 주어진 표본의 크기를 이용하여 모수를 추정하는 방법을 알아보았다.
==> 표본의 크기가 너무 작으면 왜곡된 모집단의 특성을 추정할 수 있으며, 또한 표본의 크기가 너무 크면 모집단의 특성은 잘 표현할 수 있으나 경제적,시각적,공간적인 여러 제약으로 어려움 겪을 수 있다.
==> 주어진 신뢰수준과 오차한계에 맞춰서 가장 효율적으로 표본을 추출하기 위해 표본의 크기 결정하는 문제가 중요
2. 모평균의 추정을 위한 표본의 크기
==> 신뢰구간의 길이가 d 이하인 모평균의 (1-a)100% 신뢰구간을 얻어야한다.
==> 신뢰구간의 길이
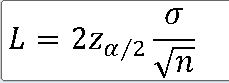
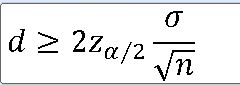
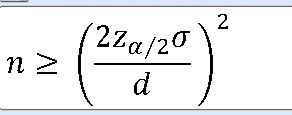
EX-01) 어느 대학의 학생과에서 학생들의 월 평균 생활비를 조사. 95% 신뢰구간의 길이가 8만원을 넘지 않게 하려면 최소한 몇 명의 학생을 조사해야 하는지 구하라(모표준편차가 20만원인 정규분포를 따름)
모표준편차 = 20
모분산 = 400
z_0.025 = 1.96
d = 8
n >= (2 * 1.96 * 20 /8)**2 = 96.04
n = 97
EX-02) 모표준편차가 2인 정규모집단의 모평균을 추정하고자 한다. 90% 신뢰구간의 길이가 0.2를 넘지 않도록 하는 최소한의 표본의 크기를 구하라.
모표준편차 = 2
모분산 = 4
z_0.05 = 1.645
2*1.645 * 모표준편차 / 루트(n) < 0.2
2*1.645*2/0.2 < 루트(n)
(2*1.645*2/0.2)**2 < n
1082.4<n
n = 1083
3. 두 모분산을 알고 있는 서로 독립인 정규모집단으로부터의 신뢰구간
==> 두 모분산을 알고 있는 서로 독립인 정규모집단으로부터 각각 크기 n, m 인 표본을 추출할때 , 모평균의 차에 대한 신뢰구간

L = 2*1.645* 루트( 모분산_1 / n + 모분산_2/m)
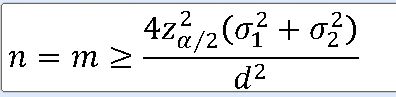
==> 두 표본의 크기가 같을때의 표본크기 구하기
EX) 두 회사에서 제조되는 1.5L 페트병에 들어 있는 음료수 양의 평균 차를 조사. 두 회사에서 제조된 음료수 표본을 동일한 개수로 선정하여 95% 신뢰구간의 길이가 0.005L 보다 작게 하기 위한 최소한의 표본의 크기를 구하라(두 회사의 음료수 양은 표준편차가 각각 0.01L와 0.02L인 정규분포를 따른다.)
d = 0.005
표준편차_1 = 0.01
표준편차_2 = 0.02
z_0.025 = 1.96
n=m >= 4 * 1.96**2 * (0.01**2 + 0.02**2) / 0.005**2 = 307.328
n = m = 308
print(4 * 1.96**2 * (0.01**2 + 0.02**2) / 0.005**2)x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)
# ex = '93.242 89.635 92.660 92.540 94.883 102.165 93.326 90.880 93.684 91.564 88.727 94.317 88.166 96.085 82.028 97.213 99.338 93.381 86.498 83.348 97.262 89.656 84.045 89.113 81.562 87.180 94.345 92.436 93.633 97.276'
# A = list(map(float, ex.split(' ')))
# print(A)
# MEANS = round(np.mean(A) ,3)
#
# VARS = 5.105**2
# STDS = round(math.sqrt(VARS/len(A)),3)
# print((z_1 * STDS / math.sqrt(len(A))))
# ax.text(2 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + f'{round(MEANS - (z_1 * STDS ),3)} ~ {round(MEANS + (z_1 * STDS ),3)}' , fontsize= 15)
#
#ax.text(2 , .35, r'$\overline{X} = $' + f'{MEANS}\n' + r'$\sigma = $' + f'{STDS}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(len(A)),2)}',fontsize=15)
ax.text(2 , .35, r'$\sigma_{1} = $' + f'{0.01}\n'+ r'$\sigma_{2} = $' + f'{0.02}\n' + f'신뢰구간 d = {0.005}',fontsize=15)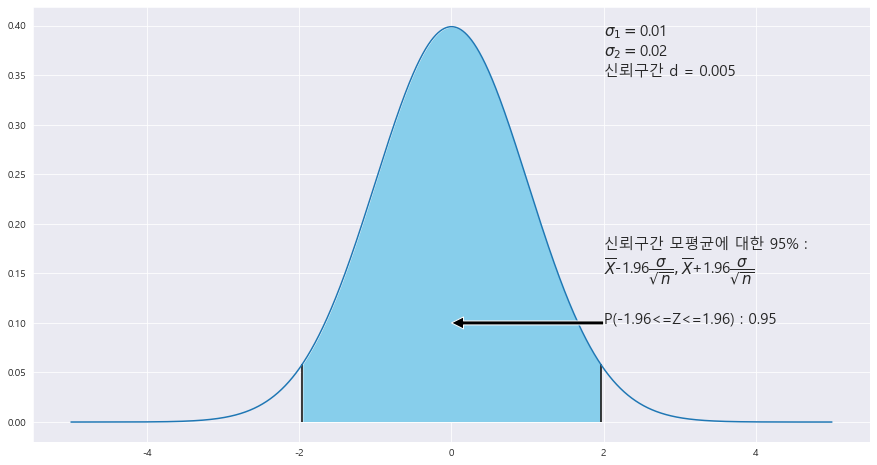
EX-02) 모표준편차가 각각 5와 3인 정규모집단의 모평균의 차에 대한 95% 신뢰구간의 길이가 2보다 작게 하기 위한 최소한의 표본의 크기를 구하라(단 , 두 표본의 크기는 동일하다.)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95#신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(-5.5 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\left( \overline{x}-\overline{y}\right)$' +f'-{z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$' +' , '+ r'$\left( \overline{x}-\overline{y}\right)$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$',fontsize=15)
d = 2 # 신뢰구간
o1 = 5 #모 표준편차 1
o2 = 3 #모 표준편차 2
ax.text(2 , .35, r'$\sigma_{1} = $' + f'{o1}\n'+ r'$\sigma_{2} = $' + f'{o2}\n' + f'신뢰구간 d = {d}',fontsize=15)
c = 2**2 * z_1**2*(o1**2 + o2**2) / d**2
ax.text(-5.5 , .1, r'$n=m\geq\dfrac{{%2d}^{2}*{%.2f}^{2}(\sigma^2_{1} + \sigma^2_{2})}{d ^{2}} = {%.3f}$'% (2 , z_1 ,c) ,fontsize=15)
print(4*z_1 * (5**2 + 3**2) / 2**2)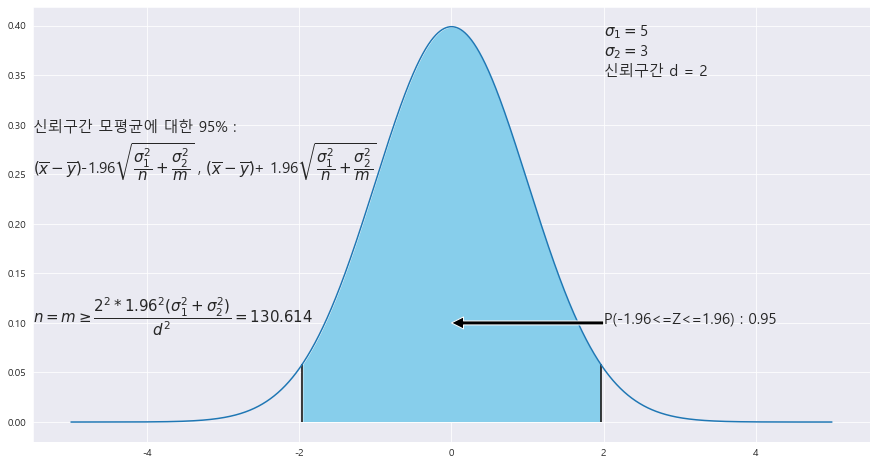
n= m = 131
4. 모비율의 추정을 위한 표본의 크기
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\widehat{p}$' +f'-{z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$' +' , '+ r'$\widehat{p}$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$',fontsize=15)
#\widehat{p}-\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}
ax.text(-5.5 , .15, f'신뢰구간 L = 2*{z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$',fontsize=15)
#
ax.text(-5.5 , .25, f'사전정보가 없는 경우 n' + r'$\geq\dfrac{z^2_{a/2}}{d^2}$',fontsize=15)
ax.text(-5.5 , .35, f'사전정보 p가 있는 경우 n' + r'$\geq\dfrac{4*z^2_{a/2}*{p}*{(1-p)}}{d^2}$',fontsize=15)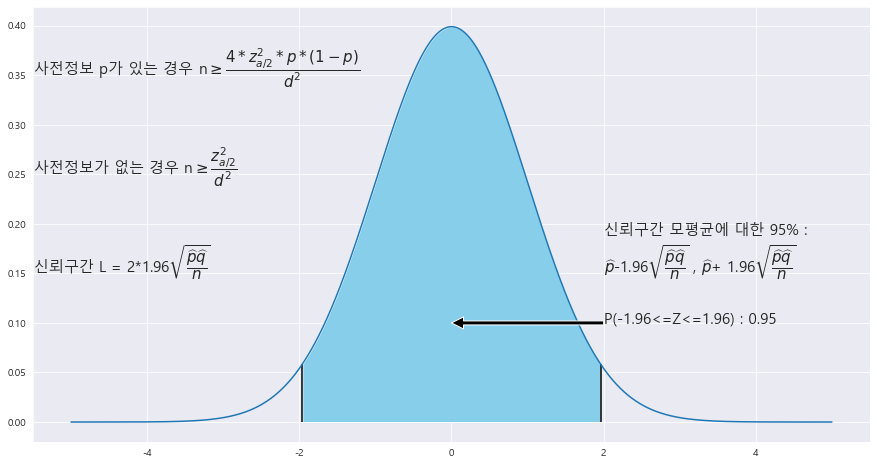
EX-01) 대통령 후보의 지지도에 대한 오차범위 +-2%에서 신뢰도 95%인 신뢰구간을 구하고자 한다면 최소한 몇 명의 유권자를 상대로 여론조사를 실시해야하는가
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰도
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\widehat{p}$' +f'-{z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$' +' , '+ r'$\widehat{p}$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$',fontsize=15)
#\widehat{p}-\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}
ax.text(-5.5 , .15, f'신뢰구간 L = 2*{z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$',fontsize=15)
d = 0.02 *2
ax.text(-5.5 , .25, f'사전정보가 없는 경우 n' + r'$\geq\dfrac{z^2_{a/2}}{d^2}$' + f' = {round(z_1**2 / d**2,2)}',fontsize=15)
ax.text(-5.5 , .35, f'사전정보 p가 있는 경우 n' + r'$\geq\dfrac{4*z^2_{a/2}*{p}*{(1-p)}}{d^2}$',fontsize=15)
d = 0.02 * 2 = 0.04
z_0.025 = 1.96
n >= 1.96**2 / 0.04**2 = 2401
EX-02) 78%가 강의 도중 핸드폰 사용경험이 있다. 오차한계 2.5%에서 대학생의 휴대폰 사용 경험 비율에 대한 95% 신뢰구간을 구하기 위한 최소한의 표본의 크기
p = 0.78
n = 1055
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰도
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\widehat{p}$' +f'-{z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$' +' , '+ r'$\widehat{p}$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$',fontsize=15)
#\widehat{p}-\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}
ax.text(-5.5 , .15, f'신뢰구간 L = 2*{z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$',fontsize=15)
d = 0.025 *2
p = 0.78
ax.text(-5.5 , .25, f'사전정보가 없는 경우 n' + r'$\geq\dfrac{z^2_{a/2}}{d^2}$',fontsize=15)
ax.text(-5.5 , .35, f'사전정보 p가 있는 경우 n' + r'$\geq\dfrac{4*z^2_{a/2}*{p}*{(1-p)}}{d^2}$' + f'= {round(4 * z_1**2 * p * (1-p) / d**2)} ' ,fontsize=15)
'기초통계 > 대표본 추정' 카테고리의 다른 글
| ★최소분산불편추정량★편의추정량★불편추정량★점추정량★기초통계학-[연습문제 -08] (0) | 2023.01.12 |
|---|---|
| ★모비율,모평균에 대한 오차한계★오차한계(신뢰구간의 절반)★기초통계학-[연습문제 -07] (0) | 2023.01.12 |
| ★string r'로 받을때 안에 값 집어넣기(변수로도 %2d)★모비율 차의 구간추정★기초통계학-[대표본 추정 -06] (0) | 2023.01.11 |
| ★모평균 차의 구간추정★기초통계학-[대표본 추정 -05] (0) | 2023.01.11 |
| ★모비율의 신뢰구간★기초통계학-[대표본 추정 -04] (0) | 2023.01.11 |