★편의 추정량★불편 추정량★기초통계학-[대표본 추정 -01]
1. 점추정
==> 임의의 모집단으로부터 대표본을 추출하면 중심극한정리에 의해 표본평균은 정규분포에 근사한다.
https://knowallworld.tistory.com/304
★중심극한정리★기초통계학-[모집단 분포와 표본분포 -05]
EX-01) 남성의 평균 결혼연령 32세 , 분산 8.41세 , 36명 임의로 선정하여 표본조사 1> 평균 결혼 연령의 근사 표본분포 n = 36 >= 30 이므로 중심극한 정리에 의하여 평균결혼 연령은 |X ~ N(32 , 8.41/ 36) 2>
knowallworld.tistory.com
==> but. 보통 모수는 알려져 있지 않다. 따라서 임의로 선정한 표본을 이용하여 알려지지 않은 모수를 보편적이고 타당한 방법으로 추정해야 한다.
==> 표본으로부터 얻은 정보를 이용하여 알려지지 않은 모집단의 정보를 추론하는 것이 추측통계학의 목적
2. 점추정의 의미
==> 통계적 추론(Statistical inference)는 표본으로부터 얻은 정보를 이용하여 과학적으로 미지의 모수를 추론하는 과정
==> 모평균 , 모분산 , 모비율 등과 같은 모수를 추론하기 위해, 크기 n인 표본을 추출하여 표본평균, 표본분산, 표본비율 등을 산출
==> 추출된 표본에 대한 표본평균, 표본분산, 표본비율과 같은 통계량의 측정값을 산출하여 미지의 모집단 분포와 모수를 추론하는 과정을 추정이라 한다.
==> 모수를 추정하기 위하여 표본으로부터 얻은 통계량을 추정량이라 한다.


==> 점추정량은 모수를 추정하기 위하여 표본에 기초에 어떤 하나의 수치를 계산하는 규칙 또는 함수 의미
==> 점추정은 모수를 추론하기 위하여 점추정량에 의해 얻은 수치
3. 바람직한 점추정
==> 바람직한 추정량이 되기 위해서는 2가지 조건이 필요
==> 추정하고자 하는 모수에 대한 추정량의 표본분포가 모수의 참값을 중심으로 이루어져야 한다.
==> 이 추정량의 표준편차가 가장 작은 것
4. 불편 추정량
==> 추정량의 평균이 모수의 참값과 같은 추정량
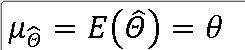
==> 정규분포를 포함한 임의의 모집단 분포에서 크기 n인 표본을 임의로 선정하면, 표본평균 |X의 평균은 모평균과 동일하다.
https://knowallworld.tistory.com/302
★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본
1. 표본평균의 표본분포(모분산을 아는 경우) ==> 표본평균에 대한 표본분포는 정규분포를 따른다. EX-01) 모평균 100 , 모분산 9인 정규모집단으로부터 크기 25인 표본을 임의로 추출 1> 표본평균 |X
knowallworld.tistory.com
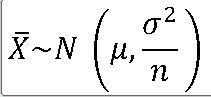
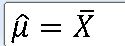
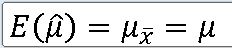
==> 표본평균 |X는 모평균에 대한 불편추정량이다.
5. 편의 추정량
==> 불편추정량이 아닌 추정량을 편의(bias)라 한다.

EX-01) 모평균이 M(뮤) 인 모집단에서 크기 3인 확률표본 {X_1 , X_2 , X_3}을 추출하여, 모평균에 대한 점추정량을 다음과 같이 정의하였다. 모평균 M(뮤)에 대한 불편추정량과 편의추정량을 구별하라.
^M_1 = (1/3)* (X_1 + X_2 + X_3)
^M_2 = (1/4) * ( (2* X_1) + X_2 + X_3)
^M_3 = (1/5) * ( X_1 + (2* X_2) + (2* X_3 ) )
^M_4 = (1/5) * ( X_1 +(2* X_2 ) + X_3)
==> X_1 , X_2 , X_3 이 동일한 모집단 분포를 따르므로 E(X_1) = E(X_2) = E(X_3) = M(뮤) 이다.
==>E(^M_1) = (1/3)* E(X_1+ X_2 + X_3) = (1/3)*[E(X_1) + E(X_2) + E(X_3) ] = (1/3) * (M + M + M ) = M
==>E(^M_2) = (1/4)* E( (2* X_1) + X_2 + X_3) = (1/3)*[ (2* E(X_1) ) + E(X_2) + E(X_3) ] = (1/4) * (2* M + M + M ) = M
==>E(^M_3) = (1/5)* E(X_1+ (2* X_2) + (2 * X_3) ) = (1/5)*[E(X_1) + (2* E(X_2) ) + (2 * E(X_3 ) ) ] = (1/5) * (M + 2*M + 2* M ) = M
==>E(^M_4) = (1/5)* E(X_1+ (2* X_2) + X_3) = (1/5)*[E(X_1) + (2* E(X_2) ) + E(X_3) ] = (1/5) * (M + 2*M + M ) = 4*M / 5
==> ^M_1 , ^M_2 , ^M_3 ==> 모평균에 대한 불편추정량
==> ^M_4 ==> 모평균에 대한 편의추정량
EX-02) 모평균이 M(뮤) 인 모집단에서 크기 2인 확률표본 {X_1 , X_2}을 추출하여, 모평균에 대한 점추정량을 다음과 같이 정의하였다. 모평균 M(뮤)에 대한 불편추정량과 편의추정량을 구별하라.
^M_1 = X_1
^M_2 = (1/2) * (X_1 +X_2)
^M_3 = (1/2) * (X_1 + 2*X_2)
^M_4 = (1/3) * (X_1 + 2*X_2)
==> X_1 , X_2 이 동일한 모집단 분포를 따르므로 E(X_1) = E(X_2) = M(뮤) 이다.
==> E(^M_1) = E(X_1) = M (불편추정량)
==> E(^M_2) = (1/2) * E(X_1 + X_2) = (1/2) * (E(X_1) + E(X_2) ) = M(불편추정량)
==> E(^M_3) = (1/2) * E(X_1 + 2*X_2) = (1/2) * (E(X_1) + 2*E(X_2) ) = 3/2 * M (편의 추정량)
==> E(^M_4) = (1/3) * E(X_1 + 2*X_2) = (1/3) * (E(X_1) + 2*E(X_2) ) = M(불편추정량)
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 대표본 추정' 카테고리의 다른 글
| ★string r'로 받을때 안에 값 집어넣기(변수로도 %2d)★모비율 차의 구간추정★기초통계학-[대표본 추정 -06] (0) | 2023.01.11 |
|---|---|
| ★모평균 차의 구간추정★기초통계학-[대표본 추정 -05] (0) | 2023.01.11 |
| ★모비율의 신뢰구간★기초통계학-[대표본 추정 -04] (0) | 2023.01.11 |
| ★신뢰구간★신뢰도★구간추정★기초통계학-[대표본 추정 -03] (0) | 2023.01.11 |
| ★불편추정량★최소분산불편추정량★유효 추정량★불편 추정량★기초통계학-[대표본 추정 -02] (0) | 2023.01.11 |