전체 글
-
[티스토리 관리] 수학식(LATEX)을 넣어보자2023.01.10
-
★모분산을 모를때는 t-분포★기초통계학-[연습문제02 -16]2023.01.09
★표본비율의 표본분포에 대한 정규분포 근사★표본비율★N(모평균 , 모평균*(1-모평균) / 전체표본개수★기초통계학-[연습문제02 -18]
20. 모비율이 p= 0.25인 모집단으로부터 크기가 각각 다음과 같은 표본을 임의로 선정한다. 표본비율이 p+-1 0.1 안에 있을 근사확률을 구하고, 표본의 크기가 커짐에 따른 확률의 변화를 비교
https://knowallworld.tistory.com/306
이항분포에 따른 정규분포의 표준정규분포화★표본비율의 표본분포★기초통계학-[모집단 분포
1.표본비율의 표본분포 EX) 이항 확률변수의 실질적인 응용 ==> 여론조사 생각 ==> 모집단을 구성하는 사람들의 어느 특정 사건을 선호하는 비율(p)를 알기 위하여 n명으로 구성된 표본을 임의 선정
knowallworld.tistory.com

1> n = 50
^p ~ N(0.25 , 0.25 * 0.75 / 50) = N(0.25 , 0.00375)
P(p-0.1 < ^p < p + 0.1) = P(-0.1 / 루트(0.00375) < Z < 0.1/루트(0.00375) = [ P(Z< 0.1/루트(0.00375) ) - P(Z<0) ] *2 = P(-1.63<= Z <= 1.63) =0.8969
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.10) / math.sqrt(0.00375 ) ,2)
# z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)) - stats.norm.cdf(0)) * 2
ax.text(1.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
2> n = 100
^p ~ N(0.25 , 0.25 * 0.75 / 100)
P(p-0.1 < ^p < p + 0.1) = P(-0.1 / 루트(0.25 * 0.75 / 100) < Z < 0.1/루트(0.25 * 0.75 / 100) = [ P(Z< 0.1/루트(0.25 * 0.75 / 100) ) - P(Z<0) ] *2 = P(-2.31 <= Z <= 2.31) = 0.9791
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.10) / math.sqrt(0.25*0.75 / 100 ) ,2)
# z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)) - stats.norm.cdf(0)) * 2
ax.text(1.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
3> n = 150
P(p-0.1 < ^p < p + 0.1) = P(-0.1 / 루트(0.25 * 0.75 / 150) < Z < 0.1/루트(0.25 * 0.75 / 150) = [ P(Z< 0.1/루트(0.25 * 0.75 / 150) ) - P(Z<0) ] *2 = P(-2.83 <= Z <= 2.83) = 0.9953
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.10) / math.sqrt(0.25*0.75 / 150 ) ,2)
# z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)) - stats.norm.cdf(0)) * 2
ax.text(1.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
21. 1484만 6천명은 국민 30%에 해당하는 비율이다. 2015년 해외여행 계획하는 사람의 비율을 조사하기 위하여 500명을 임의로 선정하여 조사.
1> 표본비율의 근사 확률분포
^p ~ N(0.3 , 0.3 * 0.7 / 500)
2> | ^p - p | 가 0.05보다 작을 확률
P( | ^p - p | < 0.05 ) = P(-0.05 < ^p - p < 0.05 ) = [ P( ^p - p < 0.05 ) - P(Z<0)] * 2 = [P( (^p-p) / 루트(0.3*0.7/500) < 0.05 / 루트(0.3*0.7/500) ) - P(Z<0)] * 2 = [ P(Z < 0.05/루트(0.3 * 0.7 / 500) ) - P(Z<0) ] * 2 = P(-2.44 <= Z <= 2.44) = 0.9853
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.05) / math.sqrt(0.3*0.7 / 500 ) ,2)
# z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)) - stats.norm.cdf(0)) * 2
ax.text(1.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))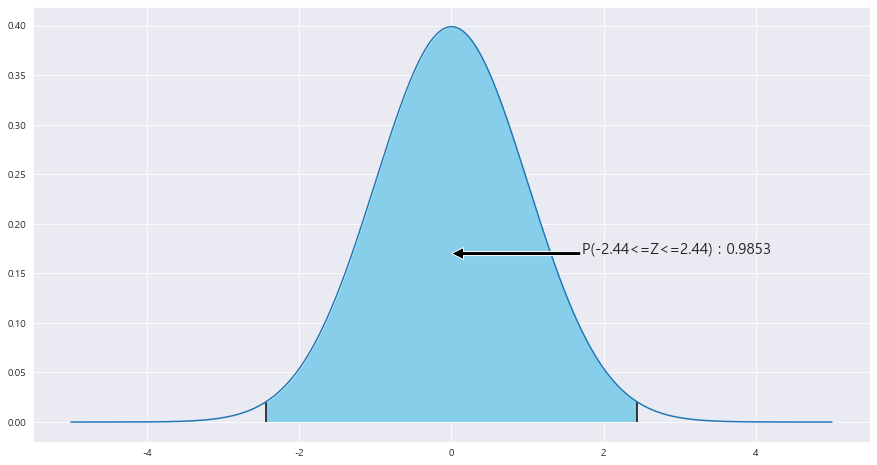
3> 표본비율 p_0보다 클 확률이 0.025인 p_0를 구하라.
P(^p > p_0 ) = P( (^p - p) / 분산 > (p_0 - p) / 분산 ) = P(Z > (p_0 - p) / 분산) = P(Z > (p_0 - 0.3 / 루트(0.3 * 0.7 / 500) ) = 0.025
p_0 = 0.3401
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
# z_1 = round((0.05) / math.sqrt(0.3*0.7 / 500 ) ,2)
# z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1- 0.025) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- scipy.stats.norm.cdf(z_1)
ax.text(2 , .12, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.3, .012), xytext=(3 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
p = Symbol('p')
a = solve( (p - 0.3)/math.sqrt(0.3*0.7/500) - 1.96)
print(a)
22. 소비자의 75%가 땅콩이나 캐러멜 등을 첨가한 초콜릿 좋아한다. 첨가물이 포함된 초콜릿을 좋아하는지 알아보기 위하여 200명의 소비자를 임의로 선정
1> 표본비율의 근사 확률분포
모비율 p = 0.75
^p ~ N(0.75 , 0.75*0.25 / 200)
2> 표본비율이 78%를 초과할 확률
P(^p > 0.78) = P(Z > 0.78 - 0.75 / 루트(0.75*0.25 / 200) ) = 1 - P(Z< 0.78 - 0.75 / 루트(0.75*0.25 / 200) ) = P(0.98 < Z) = 0.1635
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.78 - 0.75) / math.sqrt(0.75 * 0.25 / 200 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
# z_1 = round(scipy.stats.norm.ppf(1- 0.025) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- scipy.stats.norm.cdf(z_1)
ax.text(2 , .12, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.3, .012), xytext=(3 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
3> 표본비율의 95%의 백분위수
P(^p <= a ) = 0.95
P( (^p - p) / 분산 <= (a-p) / 분산 ) = P(Z<= (a-0.75 / 루트(0.75*0.25 / 200) ) = 0.95
P(Z<= 1.64) = 0.95
a = 0.8002
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
# z_1 = round((0.95 - 0.75) / math.sqrt(0.75 * 0.25 / 200 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(0.95) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1)
ax.text(2 , .12, f'P(Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .12), xytext=(1.9 , .12) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
a = Symbol('a')
b = solve( (a-0.75) / math.sqrt(0.75*0.25 / 200) - z_1)
print(b)

23. 주부들의 20%가 식품비로 주당 10만원 이상을 소비한다. 모비율 20%라는 가정 아래서 무작위로 1000명의 주부를 표본으로 선정
1> 표본비율의 근사 확률분포를 구하라.
모비율 = 0.2
n = 1000
^p ~ N(0.2 , 0.2 * 0.8 / 1000)
2> 표본비율이 p+- 0.02 안에 있을 근사확률
P(p-0.02 < ^p < p+0.02) = P(-0.02 / 루트 (0.2 * 0.8 / 1000) < Z < 0.02 / 루트 (0.2 * 0.8 / 1000) ) = [ P(Z<0.02 / 루트 (0.2 * 0.8 / 1000)) -P(Z<0) ] * 2 = P(-1.58 <= Z <= 1.58) = 0.8859
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.02) / math.sqrt(0.2*0.8 / 1000 ) ,2)
# z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)) - stats.norm.cdf(0)) * 2
ax.text(1.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
3> 표본비율의 90%, 95% 그리고 99%의 백분위수를 구하라.
P(^p <= a ) = 0.9
==> P(Z<= (a-p) / 루트 (0.2 * 0.8 / 1000) ) = P(Z<= 1.28)
a = 0.216
P(^p <= a ) = 0.95
==> P(Z<= (a-p) / 루트 (0.2 * 0.8 / 1000) ) = P(Z<= 1.64)
a= 0.22
P(^p <= a ) = 0.99
P(Z<= (a-p) / 루트 (0.2 * 0.8 / 1000) ) = P(Z<= 2.33)
a= 0.229
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
# z_1 = round((0.95 - 0.75) / math.sqrt(0.75 * 0.25 / 200 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(0.99) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1)
ax.text(2 , .12, f'P(Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .12), xytext=(1.9 , .12) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
a = Symbol('a')
b = solve( (a-0.2) / math.sqrt(0.2*0.8 / 1000) - z_1)
print(b)

24. 49.5%의 지지율, 이번선거 에서도 지난 선거의 지지율을 얻을 수 있는지 알기 위하여 400명의 유권자 상대로 조사하여 49%를 초과할 확률
모비율(p) = 0.495
n = 400
P(^p > 0.49) = P(Z > (0.49 - 0.495) / 루트(0.495* (1-0.495) / 400) ) = P(-0.2<= Z) = 0.5793
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.49 - 0.495) / math.sqrt(0.495 * (1-0.495) / 400 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
# z_1 = round(scipy.stats.norm.ppf(1- 0.025) ,2 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- scipy.stats.norm.cdf(z_1)
ax.text(2 , .12, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.3, .012), xytext=(3 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))

출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
[티스토리 관리] 수학식(LATEX)을 넣어보자
1. HTML 편집기를 통해 /BODY 태그 위에 코드 넣기
<script type="text/x-mathjax-config">
MathJax.Hub.Config({
tex2jax: {
inlineMath: [ ['$','$'], ["\\(","\\)"] ],
processEscapes: true
}
});
</script>
<script src='https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.2/MathJax.js?config=TeX-MML-AM_CHTML'></script>2. 형식
$ \widehat{p}_1 $
$$사이에 LATEX 형식으로 집어넣는다.
https://webdemo.myscript.com/views/math/index.html#
math
webdemo.myscript.com
==> 여기 사이트에선 자동으로 변환시켜준다.
★모평균을 알때는 카이제곱★중심극한정리(표본평균의 표준정규분포)★이항분포의 평균,분산★기초통계학-[연습문제02 -17]
14. 어느 주식의 가격이 매일 1단위 오를 확률은 0.52이고, 1단위 내릴 확률은 0.48이다. 첫째날 200을 투자하여 100일후의 가격은 X = 200 + for i in range(1, 101) : X_i += X_i-1
1> 주식의 등락금액 X_i , i= 1,2, ·····100의 확률함수를 구하라.
p(x) =
0.52 , x= 1
0.48 , x = -1
https://knowallworld.tistory.com/241
이항분포식★이항실험★이항분포의 평균,분산★베르누이시행★기초통계학-[Chapter05 - 이산확률
1. 이항분포 ==> 많이 사용하는 확률 모형 : 이항분포, 푸아송분포 , 초기하분포 1. 이항실험(Bionomial Experiment) ==> 실험은 N번의 시행 ==> 실험 결과는 성공(S) , 실패(F) ==> 성공 확률 : p , 실패 확률 : q
knowallworld.tistory.com
2> X_i의 평균과 분산
https://knowallworld.tistory.com/246
★푸아송분포★기하분포★초기하분포★베르누이★이산확률변수★기초통계학-[Chapter05 - 연습문
1. 이산확률변수 x의 확률분포 X = np.arange(-2,3) p_x = [0.15 , 0.25 , '-' , 0.25 , 0.3] A = pd.DataFrame([p_x] , columns = X) A.index = ['P(X = x)'] A.columns.names = ['X'] A B = (1- A.iloc[ [0], [0,1,3,4]].sum(axis=1)) B A.loc['P(X = x)' , 0] =
knowallworld.tistory.com
==> 이산확률변수의 평균과 분산 구하기
평균 : 0.52 * 1 + (-1) * 0.48 = 0.04
분산 : 1**2(0.52) + (-1)**2 *0.48 - 0.04**2 = 0.9984
3>중심극한정리에 의하여 100일 후의 가격이 210 이상일 확률
https://knowallworld.tistory.com/303
★lineplot★중심극한정리★기초통계학-[모집단 분포와 표본분포 -04]
1. 중심극한정리 ==> 정규분포가 아닌 모집단 분포로부터 복원추출로 표본 선정시 ==> 표본의 크기에 따라 표본평균의 표본분포가 변한다. ==> 모평균 뮤 , 모분산(o**2) 의 임의의 모집단으로부터
knowallworld.tistory.com
시그마_|X ~ N(0.04 * 100 , 0.9984 * 100) = N(4 , 99.84) = N(4 , 9.99**2)
X ~ N(4 + 200 , 9.99**2)
P(X>=210) = 1- P(Z<= 210 - 204 / 9.99 ) = P(0.6<=Z) = 0.2743
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((210 - 204) / 9.99 ,2)
# z_2 = round((196.82- 198) / 3.45 ,2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- (stats.norm.cdf((z_1)))
ax.text(1.71 , .17, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0.7, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))15. 음주운전 단속에서 100일간 면허 정지 처분을 받은 사람들의 혈중 알코올 농도를 측정한 결과, 평균 0.075이고, 표준편차가 0.009라고 한다. 64명이 면허 정지 처분을 받았다고 하자.
==> 표본평균의 표준정규분포
1> 면허 정지 처분을 받은 사람들의 알코올 농도의 평균에 관한 표본분포를 구하라.
n = 64
n = 64
X ~ N(0.075 , 0.009**2)
|X ~ N(0.075 , 0.009**2/ 64)
2> 평균 혈중 알코올 농도가 0.077이상일 확률
P(|X>= 0.077) = P(Z>= 0.077 - 0.075 / 루트(0.009/64) ) = 1 - P(Z<= 0.077 - 0.075 / 루트(0.009/64) ) = P(Z>0.17) = 0.4325
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.077 - 0.075) / math.sqrt(0.009**2/64) ,2)
# z_2 = round((196.82- 198) / 3.45 ,2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- (stats.norm.cdf((z_1)))
ax.text(1.71 , .17, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.1, .017), xytext=(2.1 , .14) , arrowprops = dict(facecolor = 'black'))
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
16. 주택을 소유한 모든 사람들의 화재로 인한 연간 평균 손실이 25만원이고, 표준편차는 100만원, 손실 금액은 거의 대부분이 0원이고 단지 몇몇 손실이 매우 크게 나타나는 양의 비대칭분포, 1000명 대상으로 조사
1>표본평균의 표본분포
n = 1000
뮤 = 25
모분산 = 100**2
|X ~ N(25 , 100/1000)
2>표본평균이 28만원을 초과하지 않을 확률
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((28-25) / math.sqrt(100**2/1000) ,2)
# z_2 = round((196.82- 198) / 3.45 ,2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)))
ax.text(-3.71 , .16, f'P(Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(-1.1, .14), xytext=(-2.1 , .14) , arrowprops = dict(facecolor = 'black'))
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
P(|X<28) = P(Z< 28-25 / 루트(100/1000) ) = P(Z<= 0.95) = 0.8289
17. 이종격투기 선수들의 평균 악력은 90kg , 표준편차 9kg
1> 36명의 선수를 선정시 , 평균 악력이 87kg과 93kg 사이일 근사확률
n = 36
뮤 = 90
s = 9
|X ~ N(90 , 9**2 / 36)
P(87<= |X <= 93) = [ P(93-90 / 루트(9**2/36) <= Z) - P(Z<=0) ] * 2 = P(-2<=Z<=2) = 0.9545
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((93-90) / math.sqrt(9**2 / 36 ) ,2)
# z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)) - stats.norm.cdf(0)) * 2
ax.text(1.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
2> 64명의 선수를 선정시 , 평균 악력이 87kg과 93kg 사이일 근사확률

P(-2.67<=Z<=2.67) = 0.9924
18. 모분산이 0.35인 정규모집단으로부터 크기 8인 표본을 추출한다.
https://knowallworld.tistory.com/305
★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집
1. 모분산의 표본분포 정규모집단 N(뮤 , 모분산) 으로부터 크기 n인 표본을 선정할 때 표본분산 ==> 표본분산 S**2에 대한 표본분포는 X**2-통계량 V에 대하여 자유도가 n-1인 카이제곱분포이다. https:
knowallworld.tistory.com
==> 카이제곱분포


1> 표본분산과 관련된 통계량 V = (n-1)**2 * S**2 / 모분산 의 분포를 구하라.
모분산 = 0.35
크기 = 8
V = (8-1)*S**2 / 0.35 ~ X**2(7)
2> 표본조사한 결과가 다음과 같을 때 관찰된 표본분산의 값 s_0**2을 구하라.
2.5 , 2.1 , 3.4 , 1.7 , 2.0 , 3.2 , 2.8 , 2.4
a = [2.5 , 2.1 , 3.4 , 1.7 , 2.0 , 3.2 , 2.8 , 2.4]
print(np.var(a , ddof =1 ))표본분산 = 0.3498
3> P(S**2 < s_1) = 0.05를 만족하는 s_1을 구하라.
P(X < 7*s_1 / 0.35) = 0.05
7*s_1**2 /0.35 = 14.07
s_1 = 0.1083
x = np.arange(0,30 , .001)
dof = 7
a = [2.5 , 2.1 , 3.4 , 1.7 , 2.0 , 3.2 , 2.8 , 2.4]
print(np.var(a , ddof =1 ))
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , scipy.stats.chi2(dof).pdf(x)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
X_r = scipy.stats.chi2(dof).ppf(0.05)
print(X_r)
ax.fill_between(x, scipy.stats.chi2(dof).pdf(x) , where = (x<=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(-2 , .017, 'P(X <' + r'$\chi^2_{0.95})$' + f"= {round(area,4)}" ,fontsize=12)
plt.annotate('' , xy=(1, .002), xytext=(0 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r+1 , .048, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
plt.annotate('' , xy=(2.2, .025), xytext=(5 , .044) , arrowprops = dict(facecolor = 'black'))
b = [r'$\chi^2(\eta$ = {})'.format(dof)]
plt.legend(b , fontsize = 15)
s = Symbol('s')
print(solve( (7*(s))/0.35 - X_r))
4> P(S**2 > s_2) = 0.05를 만족하는 s_2을 구하라.
x = np.arange(0,30 , .001)
dof = 7
a = [2.5 , 2.1 , 3.4 , 1.7 , 2.0 , 3.2 , 2.8 , 2.4]
print(np.var(a , ddof =1 ))
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , scipy.stats.chi2(dof).pdf(x)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
X_r = scipy.stats.chi2(dof).ppf(0.95)
print(X_r)
ax.fill_between(x, scipy.stats.chi2(dof).pdf(x) , where = (x>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = 1- scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(20 , .015, 'P(X >' + r'$\chi^2_{0.05})$' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(17, .002), xytext=(20 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 8, .01, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
plt.annotate('' , xy=(14, .01), xytext=(10 , .01) , arrowprops = dict(facecolor = 'black'))
b = [r'$\chi^2(\eta$ = {})'.format(dof)]
print(b)
plt.legend(b , fontsize = 15)
s = Symbol('s')
print(solve( (7*(s))/0.35 - X_r))
s = Symbol('s')
print(solve( (7*(s))/0.35 - X_r))s = 0.7033
19. 건강한 성인이 하루에 소비하는 물의 양은 평균 1.5L , 분산 0.04761인 정규분포 따른다. 10명의 성인을 무작위로 선정하여 하루 동안 소비하는 물의 양 측정
1> 표본분산과 관련된 통계량 V = (n-1)*S**2 / 모분산 의 분포를 구하라.
n = 10
모분산 = 0.04761
V = (10-1)*S**2 / 0.04761 ~ X**2(9)
2> 표본조사한 결과가 [1.5 , 1.6 , 1.2 , 1.7 , 1.4 , 1.3 , 1.6 , 1.3 , 1.4 , 1.7] , 관찰된 표본분산의 값 s_0**2 를 구하라.
a = [1.5 , 1.6 , 1.2 , 1.7 , 1.4 , 1.3 , 1.6 , 1.3 , 1.4 , 1.7]
print(np.var(a, ddof =1 ))
s_0**2 = 0.0312
3> 이 표본을 이용하여 통계량의 관찰값 카이제곱값을 구하라.
X_0**2 = 9* 0.0312 / 0.04761 = 5.9021
4> 표본분산 S**2이 s_0**2보다 클 확률
자유도 = 9
P(S**2 >= s_0**2) = P(9*S**2 / 0.04761 >= 9*s_0**2 / 0.04761) = P(V>= 9*s_0**2 / 0.04761) = P(V>= 5.9021) = 0.7497
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , scipy.stats.chi2(dof).pdf(x)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
X_r = scipy.stats.chi2(dof).ppf(0.95)
print(X_r)
X_r = 5.9021
ax.fill_between(x, scipy.stats.chi2(dof).pdf(x) , where = (x>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = 1- scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(20 , .015, 'P(X >' + r'$\chi^2_{0.05})$' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(17, .002), xytext=(20 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 3.5, .015, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
plt.annotate('' , xy=(5.9, .01), xytext=(2 , .01) , arrowprops = dict(facecolor = 'black'))
b = [r'$\chi^2(\eta$ = {})'.format(dof)]
print(b)
plt.legend(b , fontsize = 15)
5> P(S**2 > s_1**2) = 0.025인 s_1**2을 구하라.
P(V > 9*s_1**2 / 0.04761) = 0.025
9*s_1**2 / 0.04761 = 19.02
s_1**2 = 0.1006
x = np.arange(0,30 , .001)
dof = 9
a = [1.5 , 1.6 , 1.2 , 1.7 , 1.4 , 1.3 , 1.6 , 1.3 , 1.4 , 1.7]
print(np.var(a , ddof =1 ))
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , scipy.stats.chi2(dof).pdf(x)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
X_r = scipy.stats.chi2(dof).ppf(1- 0.025)
print(X_r)
# X_r = 5.9021
ax.fill_between(x, scipy.stats.chi2(dof).pdf(x) , where = (x>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = 1- scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(25 , .015, 'P(X >' + r'$\chi^2_{0.025})$' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(22, .002), xytext=(25 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 3.5, .008, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
plt.annotate('' , xy=(19, .005), xytext=(15 , .005) , arrowprops = dict(facecolor = 'black'))
b = [r'$\chi^2(\eta$ = {})'.format(dof)]
print(b)
plt.legend(b , fontsize = 15)
s = Symbol('s')
print(solve( (dof*(s))/0.04761 - X_r))
https://knowallworld.tistory.com/305
★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집
1. 모분산의 표본분포 정규모집단 N(뮤 , 모분산) 으로부터 크기 n인 표본을 선정할 때 표본분산 ==> 표본분산 S**2에 대한 표본분포는 X**2-통계량 V에 대하여 자유도가 n-1인 카이제곱분포이다. https:
knowallworld.tistory.com

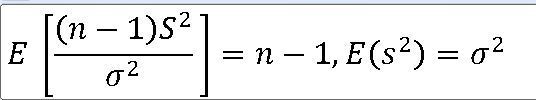
==>카이제곱분포는 정규모집단의 모분산에 대한 통계적 추론에 사용
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★표본평균의 차에 대한 절대값 처리★두 표본평균의 차에 따른 표준정규분포★기초통계학-[연습문제02 -19] (0) | 2023.01.11 |
|---|---|
| ★표본비율의 표본분포에 대한 정규분포 근사★표본비율★N(모평균 , 모평균*(1-모평균) / 전체표본개수★기초통계학-[연습문제02 -18] (1) | 2023.01.11 |
| ★모분산을 모를때는 t-분포★기초통계학-[연습문제02 -16] (0) | 2023.01.09 |
| ★Solve()이후 float로의 변환★크기를 알때/모를때의 표본평균의 표준분포★기초통계학-[연습문제02 -15] (0) | 2023.01.09 |
| ★표본평균의 정규분포(표본평균 = 모평균 , 표본분산 = 모분산/크기)★모분산 모를때 정규표본 추출★기초통계학-[연습문제02 -14] (0) | 2023.01.09 |
★모분산을 모를때는 t-분포★기초통계학-[연습문제02 -16]
11.모평균이 뮤인 정규모집단으로부터 크기 9인 표본을 임의로 추출한다. 추출된 표본의 표본분산이 25일때 P( | |X - 뮤 | < k) = 0.9를 만족하는 상수 k를 구하라.
모분산 = 모름
크기 = 9
표본분산 = 25
==> 모분산을 모를때는 t-분포를 활용한다.
https://knowallworld.tistory.com/302
★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본
1. 표본평균의 표본분포(모분산을 아는 경우) ==> 표본평균에 대한 표본분포는 정규분포를 따른다. EX-01) 모평균 100 , 모분산 9인 정규모집단으로부터 크기 25인 표본을 임의로 추출 1> 표본평균 |X
knowallworld.tistory.com
자유도 = 9-1 = 8

T = (|X - 뮤) / (25/루트(9)) ~ t(8)
P( | |X-뮤 | < k ) = P ( |T| < t_0 ) = 0.90
t_0 = k / (25/루트(9))
P(T>t_0) = 0.05
X = np.arange(-5,5 , .01)
fig = plt.figure(figsize=(15,8))
dof_2 = [8] #자유도
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
t_r = scipy.stats.t(dof_2).ppf(1- 0.05)
print(t_r)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
plt.annotate('' , xy=(2.0, .007), xytext=(2.5 , .16) , arrowprops = dict(facecolor = 'black'))
ax.text(1.71 , .17, r'$P(T>t_{0.05})$' + f'= {0.05}',fontsize=15)
ax.text(t_r - 1 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
k = Symbol('k')
k = solve((math.sqrt(25/9)) * t_r[0] - k)
print(k)
k = Symbol('k')
k = solve((math.sqrt(25/9)) * t_r[0] - k)
print(k)t_0 = 1.86
k = 3.1
12. 평균 198인 정규분포 , 25명을 무작위로 선정하여 측정 결과 표본평균이 197, 표본평균편차가 3.45
1> 표본평균 |X에 대한 표본분포를 구하라.
==>모분산을 모른다.
|X ~ N (197 , 모분산/ 25)
루트 (모분산/25) = 3.45
모분산 = 297.562
P(196.82 <= |X <= 199.18) = [P(199.18 - 197 / 3.45 ) - P(Z<=0)] * 2
==> 틀리다.
T = (|X - 198) / (3.45 / 5 ) ~ t(25-1)
2> 표본평균이 196.82와 199.18 사이일 근사확률을 구하라.
P(196.82 <= T <= 199.18) = P( (196.82 - 197) / ( (3.45 / 5 ) < T <= (199.18 - 197) / ( (3.45 / 5 ) ) = ( P(T<=1.71) - P(T<=0) ) * 2 = P(-1.71 <= T <= 1.71) = 0.9
X = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
dof_2 = [24] #자유도
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
#t_r = scipy.stats.t(dof_2).ppf(1- 0.05)
t_r = round( (199.18 - 198) / ( (3.45 / 5 ) ) , 2)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X<=t_r) & (X>=-t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.vlines(x = -t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(-t_r) , colors = 'black')
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
plt.annotate('' , xy=(0, .16), xytext=(1.5 , .16) , arrowprops = dict(facecolor = 'black'))
area = (scipy.stats.t(dof_2).cdf(t_r) - scipy.stats.t(dof_2).cdf(0) ) * 2
ax.text(1.71 , .17, r'$P(T>t_{})$' + f'= {round(area[0], 2)}',fontsize=15)
ax.text(t_r - 0.8 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
ax.text(-t_r - 0.8 , 0.02 , r'$t_r$' + f'= {-t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
3> 표본평균이 상위 2.5%인 경계수치를 구하라.
t_r = 2.064 = x- 198 / (3.45 / 5 )
x = 199.424
X = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
dof_2 = [24] #자유도
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
t_r = scipy.stats.t(dof_2).ppf(1- 0.025)
# t_r = round( (199.18 - 198) / ( (3.45 / 5 ) ) , 2)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
# ax.vlines(x = -t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(-t_r) , colors = 'black')
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
plt.annotate('' , xy=(2.5, .005), xytext=(2.5 , .16) , arrowprops = dict(facecolor = 'black'))
area = 1- scipy.stats.t(dof_2).cdf(t_r)
ax.text(1.71 , .17, r'$P(T>t_{0.025})$' + f'= {round(area[0], 3)}',fontsize=15)
ax.text(t_r - 0.8 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
# ax.text(-t_r - 0.8 , 0.02 , r'$t_r$' + f'= {-t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)

13. 평균 5000시간인 정규분포, 전구 16개 구입하여 , |x = 4800시간 , s = 1000시간
1> 표본평균 |X의 표본분포를 구하라.
모분산 모른다.
|X - 5000 / 루트(1000**2 / 16 ) ~ t(16-1)
2> 이 표본을 이용하여 P(| |X -5000 | < x_0 ) = 0.9를 만족하는 x_0를 구하라.
n = 16
자유도 = 15
(P( (x_0) / 루트(1000**2 / 16 ) < T ) - 0.5) * 2 = 0.9
P( (x_0) / 루트(1000**2 / 16 ) < T ) = 0.95
t_0.05 = (x_0) / 루트(1000**2 / 16 ) = 1.753
x_0 = 438.25
X = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
dof_2 = [15] #자유도
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
t_r = scipy.stats.t(dof_2).ppf(0.95)
# t_r = round( (199.18 - 198) / ( (3.45 / 5 ) ) , 2)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
# ax.vlines(x = -t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(-t_r) , colors = 'black')
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
plt.annotate('' , xy=(2.5, .005), xytext=(2.5 , .16) , arrowprops = dict(facecolor = 'black'))
area = 1- scipy.stats.t(dof_2).cdf(t_r)
ax.text(1.71 , .17, r'$P(T>t_{0.05})$' + f'= {round(area[0], 3)}',fontsize=15)
ax.text(t_r - 0.8 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
# ax.text(-t_r - 0.8 , 0.02 , r'$t_r$' + f'= {-t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
x = Symbol('x')
print(solve(1.753 * math.sqrt(1000**2/16) - x))
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
★Solve()이후 float로의 변환★크기를 알때/모를때의 표본평균의 표준분포★기초통계학-[연습문제02 -15]
8. 평균 = 198 , 분산 = 36인 정규분포
1> 임의로 1명을 선정하였을때, 이 사람의 혈압이 196과 200사이일 확률
X ~ N(198 , 36)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((200-198) / math.sqrt(36) ,2)
# z_2 = round((52-50) / math.sqrt(144/25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>= -z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)) - stats.norm.cdf(0)) * 2
ax.text(1.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))P(196<= X <= 200) = P( (196-198) / 6 <= Z <= (200-198) / 6 ) = [P(Z<= (200-198) / 6 ) - P(Z<= 0)] *2 =P(-0.33 <= Z <= 0.33) = 0.2586

2> 100명을 임의로 선정하여 표본을 만들때, 표본평균 |X의 표본분포를 구하라.
X ~ N(198 , 36)
|X ~ N(198 , 36/100)
3> 표본평균이 196과 200 사이일 확률
P(196<= |X <= 200) = P( (196 -198) / 루트(36/100) <= Z <= (200-198)/ 루트(36/100) ) = [ P(Z<=(200-198)/ 루트(36/100) ) - P(Z<=0) ] * 2 = P(-3.33<=Z<= 3.33) = 0.9991
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((200-198) / math.sqrt(36/100) ,2)
# z_2 = round((52-50) / math.sqrt(144/25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>= -z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)) - stats.norm.cdf(0)) * 2
ax.text(1.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
4> 표본평균이 뮤+- (모표준편차/5) 사이일 확률
모표준편차 = 6
표본평균편차 = 루트(36/100)
P( 뮤- (모표준편차/5) <= |X <= 뮤+ (모표준편차/5) ) = [ P(Z<= [뮤 + (모표준편차/5) - 뮤] / 표본평균편차 ) - P(Z<= 0) ] * 2 = [ P(Z<= (모표준편차 / (표본평균편차*5) ) - P(Z<=0) ] * 2 = P(-2<= Z <= 2) = 0.9545
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((6/5) / math.sqrt(36/100) ,2)
# z_2 = round((52-50) / math.sqrt(144/25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>= -z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)) - stats.norm.cdf(0)) * 2
ax.text(1.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
9. 1km당 0.5g 이하일 것을 요구. 유럽에 수출하기 위하여 국내에서 생산된 특정 모델의 자동차에서 내뿜는 배기가스에 포함된 질소산화물은 1km당 평균 0.45g, 표준편차 0.05g인 정규분포를 따른다.
1> 이 모델의 자동차 한 대를 무작위로 선정했을 때, 유럽연합의 기준에 포함될 확률
X ~ N(0.45 ,0.05**2)
P(X<=0.5) = P(Z<= (0.5- 0.45) / 0.05 ) = P(Z<= 1.0) = 0.6827
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.5- 0.45) / math.sqrt(0.05**2) ,2)
# z_2 = round((52-50) / math.sqrt(144/25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)))
ax.text(1.71 , .17, f'P(Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
# ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
2> 9대의 자동차를 무작위로 선정했을때, 표본평균이 유럽연합의 기준에 포함될 확률
n= 9
X ~ N(0.45 , 0.05**2)
|X ~ N(0.45 , 0.05**2 / 9 )
P(|X <= 0.5) = P(Z <= (0.5 -0.45) / 루트(0.05**2 / 9 ) ) = P(Z<= 3.0) = 0.9973
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.5- 0.45) / math.sqrt(0.05**2 / 9 ) ,2)
# z_2 = round((52-50) / math.sqrt(144/25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)) - stats.norm.cdf(0)) * 2
ax.text(1.71 , .17, f'P(Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
# ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
10. 평균 35시간, 표준편차 5.5시간 , 25개를 임의로 수거해서 조사==> 표본평균
n = 25
|X ~ N(35 , (5.5**2)/25)
1> 평균 사용시간이 36시간 이상일 확률
P(|X>=36) = 1 - P(|X<=36) = 1 - P(Z<= (36-35) / 루트((5.5**2)/25) ) = P(Z>=0.91) = 0.1814
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((36-35) / math.sqrt(5.5**2 / 25 ) ,2)
# z_2 = round((52-50) / math.sqrt(144/25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- stats.norm.cdf(z_1)
ax.text(2.31 , .08, f'P(Z>={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(1.1, .08), xytext=(2.2 , .08) , arrowprops = dict(facecolor = 'black'))
# ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))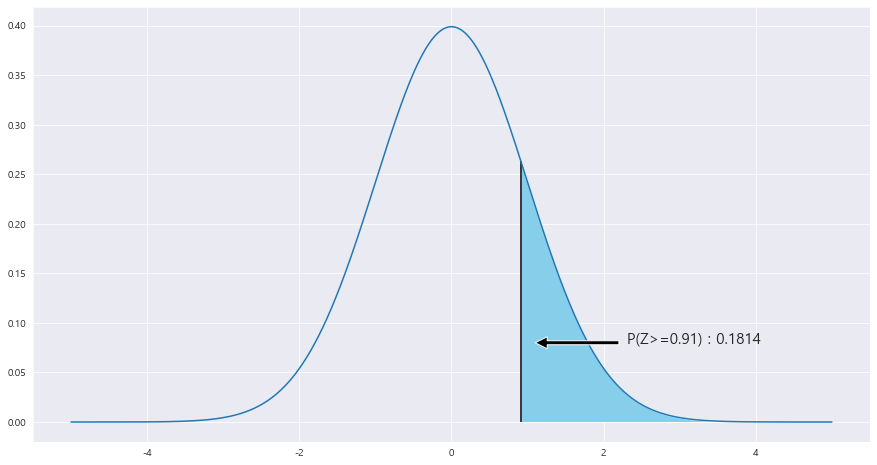
2> 평균 사용시간이 33시간 이하일 확률
P(|X<=33) = P(Z<= (33-35) /루트((5.5**2)/25)) = P(Z<= -1.82) = 0.0344
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((33-35) / math.sqrt(5.5**2 / 25 ) ,2)
# z_2 = round((52-50) / math.sqrt(144/25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = stats.norm.cdf(z_1)
ax.text(-5.31 , .04, f'P(Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(-2.1, .04), xytext=(-3.2 , .04) , arrowprops = dict(facecolor = 'black'))
# ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))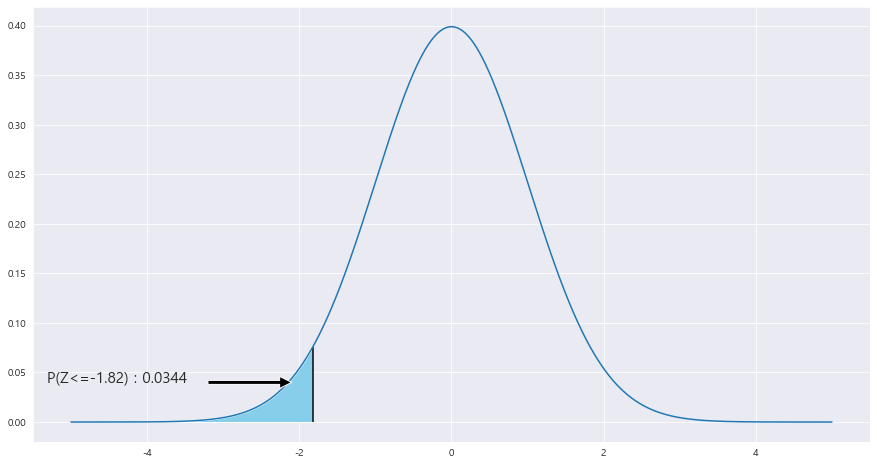
3> 평균 사용시간이 34.5시간과 35.5시간 사이의 확률
|X ~ N(35 , (5.5**2)/25)
P(34.5 <= |X <= 35.5) = P(Z <=(35.5-35) / 루트( (5.5**2)/25 ) ) ) - P(Z<=0) ) * 2 = P(-0.45<= Z <= 0.45) = 0.3473
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((35.5- 35) / math.sqrt(5.5**2 / 25 ) ,2)
# z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=z_2) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)) - stats.norm.cdf(0)) * 2
ax.text(1.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
4> 평균 사용시간이 x_0보다 클 확률이 0.025인 x_0를 구하라.
|X ~ N(35 , (5.5**2)/25)
P(|X > x_0) = 0.025
P(|X< x_0) = P(Z<= (x_0 -35)/ 루트(5.5**2 / 25) ) = P(Z>= 1.96) = 0.025
x_0 = 37.1559
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = 2
x_0 = Symbol('x_0')
x_0 = solve( (x_0 -35) / math.sqrt(5.5**2 / 25) - scipy.stats.norm.ppf((1-0.025)))
# print(x_0[0])
z_1 = round( float( (x_0[0] - 35) / math.sqrt(5.5**2 / 25)),2)
#
print(z_1)
print(type(z_1))
# z_2 = round((52-50) / math.sqrt(144/25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- stats.norm.cdf(z_1)
ax.text(2.31 , .08, f'P(Z>={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.2, .02), xytext=(2.2 , .08) , arrowprops = dict(facecolor = 'black'))
# ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))==> SOLVE() 이후 FLOAT()으로의 변환

출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★모평균을 알때는 카이제곱★중심극한정리(표본평균의 표준정규분포)★이항분포의 평균,분산★기초통계학-[연습문제02 -17] (1) | 2023.01.10 |
|---|---|
| ★모분산을 모를때는 t-분포★기초통계학-[연습문제02 -16] (0) | 2023.01.09 |
| ★표본평균의 정규분포(표본평균 = 모평균 , 표본분산 = 모분산/크기)★모분산 모를때 정규표본 추출★기초통계학-[연습문제02 -14] (0) | 2023.01.09 |
| ★확률질량함수의 평균 분산★그룹화자료의 평균과 분산이 아닌 확률질량함수이다!!!★이산균등분포★기초통계학-[연습문제01 -13] (0) | 2023.01.07 |
| ★표본비율의 차에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -12] (0) | 2023.01.07 |
3. 뮤 = 50이고 모표준편차가 다음과 같은 모집단으로부터 크기 25인 확률표본을 선정할 때, 표본평균이 49와 52사이일 확률
https://knowallworld.tistory.com/302
★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본
1. 표본평균의 표본분포(모분산을 아는 경우) ==> 표본평균에 대한 표본분포는 정규분포를 따른다. EX-01) 모평균 100 , 모분산 9인 정규모집단으로부터 크기 25인 표본을 임의로 추출 1> 표본평균 |X
knowallworld.tistory.com

1> 모표준편차 = 4
n = 25
|X ~ N(50 , 4**2/25)
P(49<=|X<=52) = P(|X<= 52) - P(|X<=49) = P(Z<= (52-50) / 루트(16/25) ) - P(Z<= (49-50) / 루트(16/25) ) = P(-1.25 <=Z <=2.5) = 0.8881
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((52-50) / math.sqrt(16/25) ,2)
z_2 = round((49-50) / math.sqrt(16/25) ,2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=z_2) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area_1 = ( stats.norm.cdf(z_1) - stats.norm.cdf(z_2) )
ax.text(2.71 , .17, f'P({z_2}<=Z<={z_1}) : {round(area_1,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(2.5 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))

2> 모표준편차 = 9
n = 25
|X ~ N(50 , 9**2/25)
P(49<=|X<=52) = P(|X<= 52) - P(|X<=49) = P(Z<= (52-50) / 루트(81/25) ) - P(Z<= (49-50) / 루트(81/25) ) = P(-0.56 <=Z <=1.11) = 0.5788

3> 모표준편차 = 12
n = 25
|X ~ N(50 , 12**2/25)
P(49<=|X<=52) = P(|X<= 52) - P(|X<=49) = P(Z<= (52-50) / 루트(144/25) ) - P(Z<= (49-50) / 루트(144/25) ) = P(-0.42 <=Z <=08.83) = 0.4595

4. 뮤 = 50이고 모표준편차가 5인 정규모집단으로 부터 크기 n인 확률표본을 선정할때 , 표본평균이 49와 51사이일 확률
1> n = 16
|X ~ N(50 , 5**2/16)
P(49<=|X<51) = P( ( (49-50) / 루트(5**2/16) ) <= Z <= ( (51-50) / 루트(5**2)/16 ) = [P(1/루트(5**2/16) <= Z) - P(Z<=0)] * 2 = P(-0.8 <= Z <= 0.8) = 0.5763
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((51-50) / math.sqrt(25/16) ,2)
# z_2 = round((52-50) / math.sqrt(144/25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>= -z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = (stats.norm.cdf((z_1)) - stats.norm.cdf(0)) * 2
ax.text(1.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))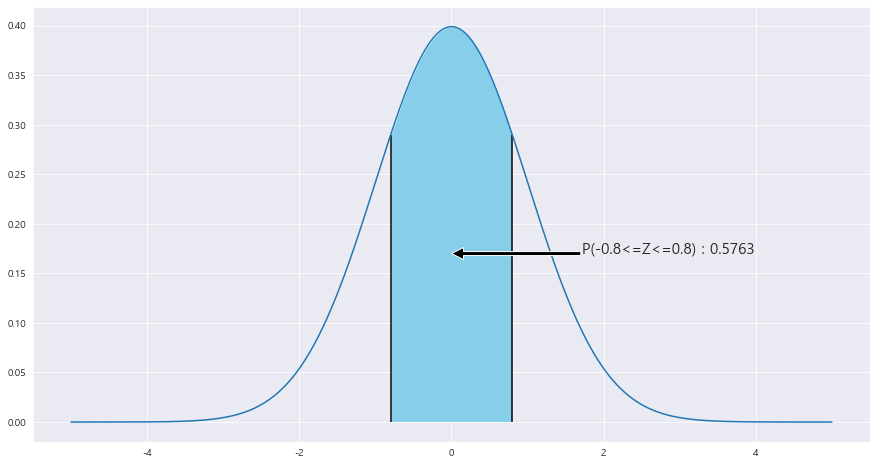
2> n = 49
P(-1.4 <= Z <= 1.4) = 0.8385

3> n = 64
P(-1.6<=Z<=1.6) = 0.8904

5. 뮤 = 45이고 모분산이 9인 정규모집단으로 부터 크기 64인 표본을 추출할때 , 표본평균이 어떤 상수 K보다 작을 확률이 0.95일때, 상수 k를 구하라.
|X ~ N(45 , 9/64)
P(|X<K) = 0.95
P(Z< K-45 / 루트(9/64) ) = 0.95
K-45/루트(9/64) = 1.645
k = Symbol('k')
a = solve( (k-45) / math.sqrt(9/64) - 1.645)
print(a)k = 45.616
6. 모분산이 36인 정규모집단에서 크기 16인 표본을 임의로 추출할때 , P(| |X- 뮤| >= 3)을 구하라.
1- P( -3 <= |X -뮤 <= 3) = 1- P(-3+뮤 <= |X <= 3+ 뮤) = 1- P( -3 / 루트(36/16) <= Z <= 3 / 루트(36/16) ) = 1- P(-2 <= Z <= 2) = 1- 0.9545 = 0.0455
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((3) / math.sqrt(36/16) ,2)
# z_2 = round((52-50) / math.sqrt(144/25) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) | (x<= -z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 0.5 - ((stats.norm.cdf((z_1)) - stats.norm.cdf(0)))
ax.text(2.61 , .05, f'P({z_1}>=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.3, .017), xytext=(2.5 , .05) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(-3.71 , .055, f'P(Z<={-z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(-2.3, .017), xytext=(-2.5 , .05) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
plt.annotate('' , xy=(0, .2), xytext=(-2.5 , .08) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(0, .2), xytext=(2.5 , .08) , arrowprops = dict(facecolor = 'black'))
ax.text(-1 , .21, f'P({-z_1}<=Z<={z_1}) : {round(area*2,4)}',fontsize=15)
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
7. 모평균이 20 , 모표준편차가 6인 정규모집단에서 크기 n인 표본을 임의로 추출할때, 표본표준편차가 1.5라 한다. 표본의 크기 n을 구하라.
X ~ N(20 , 6**2 )
|X ~ N(20 , 36/n)
n = Symbol('n')
a = solve(36/n - 1.5**2)
print(a)루트(36/n) = 1.5
n = 16
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★모분산을 모를때는 t-분포★기초통계학-[연습문제02 -16] (0) | 2023.01.09 |
|---|---|
| ★Solve()이후 float로의 변환★크기를 알때/모를때의 표본평균의 표준분포★기초통계학-[연습문제02 -15] (0) | 2023.01.09 |
| ★확률질량함수의 평균 분산★그룹화자료의 평균과 분산이 아닌 확률질량함수이다!!!★이산균등분포★기초통계학-[연습문제01 -13] (0) | 2023.01.07 |
| ★표본비율의 차에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -12] (0) | 2023.01.07 |
| ★F-분포★두 표본분산의 비에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -11] (1) | 2023.01.07 |
[외교부 인턴 일지- d+128 2022.01.08]데이터 분석 청년인재 양성 사업
#N= 366 , 평균 = 899.39 , 표준편차 = 34.72 , 내점수 = 926.42
#내점수의 퍼센테이지
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((926.42 - 899.39) / 34.72, 2)
area = 1- scipy.stats.norm.cdf(z_1)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
ax.text(1.71 , .15, f'P({z_1}<=Z) : {round(area,4)} , 등수 : {366* round(area,4)} ',fontsize=15)
plt.annotate('' , xy=(2, .017), xytext=(2 , .14) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
https://knowallworld.tistory.com/253
stats.norm.cdf()★표준정규분포 넓이 구하기!!★ax.lineplot★정규분포(Normal Distribution)★기초통계학-[Ch
1. 정규분포(Normal Distribution) ==> 자료 집단에 대한 도수히스토그램은 자료의 수가 많을 수록 종 모양에 가까운 형태로 나타난다. ==> 종 모양의 확률분포를 정규분포라고 한다. 1>정규분포의 성질
knowallworld.tistory.com
'인턴일지 > 외교부_일지' 카테고리의 다른 글
| [외교부 인턴 일지- d+140 2022.01.20]데이터 분석 청년인재 양성 사업 (1) | 2023.01.20 |
|---|---|
| [외교부 인턴 일지- d+139 2022.01.19]데이터 분석 청년인재 양성 사업 (0) | 2023.01.19 |
| [외교부 인턴 일지- d+115 2022.12.26]데이터 분석 청년인재 양성 사업 (0) | 2022.12.29 |
| [외교부 인턴 일지- d+109 2022.12.23]데이터 분석 청년인재 양성 사업 (1) | 2022.12.23 |
| [외교부 인턴 일지- d+100 2022.12.14]데이터 분석 청년인재 양성 사업 (0) | 2022.12.14 |
JETBRAINS(INTELLIJ , DATASPELL 등) 한국어 설치하는 방법
https://plugins.jetbrains.com/plugin/13711-korean-language-pack------
Korean Language Pack / 한국어 언어 팩 - IntelliJ IDEs Plugin | Marketplace
The Korean Language Pack localizes the UI of IntelliJ IDEA, AppCode, CLion, DataGrip, GoLand, PyCharm, PhpStorm, RubyMine, and WebStorm into Korean.
plugins.jetbrains.com
==> INSTALL
==> IDE 를 킨다.


플러그인 ==> 존재
==> IDE 껐다 키면 된다.
'IT에대해 알아보자 > 쥬피터(ANACONDA)' 카테고리의 다른 글
| [DATASPELL SSH 연결 하기] (0) | 2024.06.21 |
|---|---|
| ★TensorFlow 설치★Keras 설치★ in Anaconda Prompt (0) | 2022.11.28 |
| anaconda 파이썬 업데이트시 생기는 오류 해결 (0) | 2022.10.19 |
| Could not fetch URL https://pypi.org/simple/missingno/ (0) | 2022.09.13 |
| 쥬피터(아나콘다) 가상화 사용하기(anaconda Virtual environment) (0) | 2022.07.25 |