★두 표본평균의 차에 대한 표본분포(모분산 모를때)★중심극한정리 활용★이표본의 표본분포★기초통계학-[모집단 분포와 표본분포 -09]

1. 두 표본평균의 차에 대한 표본분포(두 모분산을 모르는 경우)

https://knowallworld.tistory.com/302

★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본

==> 대부분 모집단의 모분산이 알려지지 않는다.

 

==> 단일 표본에 대한 표본평균은 t-분포와 관련되는 것을 알 수 있다.

 

==> 이 표본인 경우에도 두 표본평균의 차는 t-분포를 사용한다.

 

 

이표본의 t-분포에 대한 특징

 

㉠ 두 모집단분포는 정규분포이다.

 

㉡ 두 모분산은 알려지지 않았으나 동일하다.

 

㉢ 두 표본분산을 공동으로 사용한다.

 

 

==> 합동표본분산(Pooled sample Variance)

 

합동 표본분산

합동 표본분산_2

 

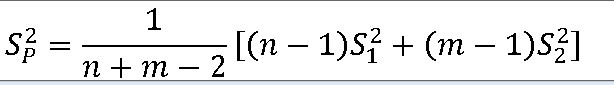
==> 실제로 모분산이 알려지지 않으므로, 공동으로 사용하는 표본표준편차로 대치한다. 

 

==> 서로 독립인 집단에서 공동으로 사용한다는 의미

 

 

==> 미지의 동일한 모분산을 가지는 서로 독립인 두 정규 모집단에서 각각 크기가 n과 m인 두 확률표본을 추출할때, 두 표본평균의 차 |X - |Y는 자유도 n+m-2 인 t-분포를 따른다.

 

 

https://knowallworld.tistory.com/259

★scipy.stats.t(자유도).ppf()★t-분포★기초통계학-[Chapter06 - 연속확률분포-07]

 

EX-01) 타이어의 공정방법에 따른 예전 방법과 새로운 방법으로 생산한 타이어의 수명 차이를 알아본다.

평균 수명이 동일하고, 표본평균은 새로 생산한 타이어가 예전 방식으로 생산한거 보다 1.518km이상 더클 확률(두 독립집단은 동일한 분산을 갖는 정규분포를 따른다.)

 

 

새로운방법 : [65.4 , 63.6 , 61.5 , 62.6 , 61.1 , 60.4 , 62.5 , 62.4 , 63.7]

예전 방법 : [59.2 , 60.6 , 56.2 , 62.0 , 58.1 , 57.7 , 58.1]

 

# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
#%%
new =  [65.4 , 63.6 , 61.5 , 62.6 , 61.1 , 60.4 , 62.5 , 62.4 , 63.7]

old = [59.2 , 60.6 , 56.2 , 62.0 , 58.1 , 57.7 , 58.1]

print(f'new 평균 : {np.mean(new)}')
print(f'new 분산 : {np.var(new , ddof = 1)}')

print(f'old 평균 : {np.mean(old)}')
print(f'old 분산 : {np.var(old , ddof=1)}')

새로운 타이어의 표본평균 : 62.57

새로운 타이어의 표본분산 : 2.3

n = 9

 

 

옛날 타이어의 표본평균 : 58.84

옛날 타이어의 표본분산 : 3.762

m = 7

 

 

==> 합동표본분산

 

s_p**2 = 1/(9+7-2) * [(9-1)*2.3 + (7-1) * 3.762] = 2.926

s_p = 1.71

 

 

s_|x-|y = s_p * 루트( (1/n) + (1/m) ) = 1.71 * 루트( (1/9) + (1/7) ) = 0.8617

 

자유도 = n+m-2

 

|X - |Y는 자유도 14인 t-분포를 따른다. 

 

P( (|X-|Y) > 1.518 )

 

U = |X - |Y

 

뮤_x - 뮤_y = 0

 

s = 0.8617

P(U > 1.518) = P(T > 1.518 - 0 / 0.8617) = P(T>= 1.76) = 0.05

 

X = np.arange(-5,5 , .01)

fig = plt.figure(figsize=(15,8))
dof_2 = [14] #자유도

ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
#t_r =  scipy.stats.t(dof_2).ppf(1- 0.05)
t_r = 1.76
print(t_r)

area = round(float(1- scipy.stats.t(dof_2).cdf(1.76)),2)

ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔

ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')

plt.annotate('' , xy=(3.0, .007), xytext=(2.5 , .16)  , arrowprops = dict(facecolor = 'black'))

ax.text(1.71 , .17, r'$P(T>t_{0.05})$' + f'= {area}',fontsize=15)


ax.text(t_r - 0.8 , 0.02 , r'$t_r$' + f'= {t_r}'  , fontsize = 13)


b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)

합동표본분포에 따른 t-분포표

EX-02) 자동차 공정라인에 따른 평균 시간 차이 여부 파악. 공정라인 A의 표본평균이 공장라인 B의 표본평균보다  1.66분 이상일 확률(엔진을 올리는 시간을 정규분포를 따르고, 단위는 분)

 

 

공정라인 A: [3 , 7 , 5 , 8 , 4 , 3]

공정라인 B : [2 , 4 , 9 , 3, 2]

 

A = [3 , 7 , 5 , 8 , 4 , 3]

B = [2 , 4 , 9 , 3, 2]

print(f'A 평균 : {np.mean(A)}')
print(f'A 분산 : {np.var(A , ddof = 1)}')

print(f'B 평균 : {np.mean(B)}')
print(f'B 분산 : {np.var(B , ddof=1)}')

A의 평균 : 5

A의 분산 : 4.4

n = 6

 

 

 

B의 평균: 4

B의 분산 : 8.5

m = 5

 

VARS = (1/9) * ((5 *4.4) + (4*8.5))

STDS = math.sqrt(VARS)

print(VARS)
print(STDS)

s_p**2 = (1 / (n+m-2) ) * [ (n-1) * s_A**2 ) + (m-1) * s_B**2 ) ]  = (1/9) *  [(5 * 4.4) + (4 * 8.5) ]  = 6.22

 

s_p = 2.494

 

print(STDS * math.sqrt( (1/6) + (1/5)))

S = s_p * (루트 ( (1/6) + (1/5) ) = 1.51

 

 

뮤_|x = 뮤_|y

뮤_|x - 뮤_|y = 0

자유도 = n + m - 2 = 9

P(|X - |Y >= 1.66) = P(T >= (1.66 -0) / 1.51 ) = 0.15

 

X = np.arange(-5,5 , .01)

fig = plt.figure(figsize=(15,8))
dof_2 = [9] #자유도

ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
#t_r =  scipy.stats.t(dof_2).ppf(1- 0.05)
t_r = round(1.66 / 1.51 ,2)
print(t_r)

print(scipy.stats.t(dof_2).ppf(0.85))

area = round(float(1- scipy.stats.t(dof_2).cdf(t_r)),2)

ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔

ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')

plt.annotate('' , xy=(3.0, .007), xytext=(2.5 , .16)  , arrowprops = dict(facecolor = 'black'))

ax.text(1.71 , .17, r'$P(T>t_{0.15})$' + f'= {area}',fontsize=15)


ax.text(t_r - 0.8 , 0.02 , r'$t_r$' + f'= {t_r}'  , fontsize = 13)


b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)

합동표본분포에 따른 t-분포표

==> t_0.15 ==> 꼬리확률 15% , t_0.15 = 0.15

 

출처 :  [쉽게 배우는 생활속의 통계학]  [북스힐 , 이재원] 

※혼자 공부 정리용