★표본비율의 차에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -12]

1. 두 표본비율의 차에 대한 표본분포

 

==> 서로 독립이고 모비율이 각각 p_1 , p_2인 두 모집단에서 각각 크기 n,m인 표본 선정

 

 

==> 표본의 크기가 충분히 크다면

 

https://knowallworld.tistory.com/301

★모비율★표본비율★기초통계학-[모집단 분포와 표본분포 -02]

https://knowallworld.tistory.com/306

이항분포에 따른 정규분포의 표준정규분포화★표본비율의 표본분포★기초통계학-[모집단 분포

==> 표본비율의 표본분포의 정규분포 근사

표본비율

두 표본비율의 차에 대한 표본정규분포

 

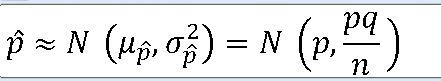
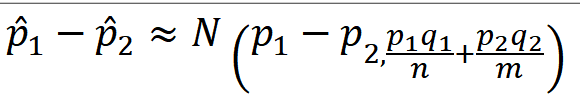
EX-01) 무죄를 주장하는 피고인이 교도소로 보내지는 비율은 84.7% , 유죄를 인정하는 피고인 중에 교도소로 보내지는 비율은 52.1%. 무죄를 주장하는 피고인 150명과 유죄를 인정하는 피고인 120명 선정. 무죄를 주장하는 피고인 중에 교도소로 보내지는 비율을 ^p , 유죄를 인정하는 피고인 중에 교도소로 보내지는 비율을 ^p_2 라 할때 ^p_1 - ^p_2가 30%를 초과할 확률

 

 

무죄 주장 ==> 교도소 갈 확률 ==> ^p_1 = 0.847

 

유죄 주장 ==> 교도소 갈 확률 ==> ^p_2 = 0.521

 

n = 150

m= 120

 

 

 

^p_1 - ^p_2 = 0.847 - 0.521 = 0.326

 

 

표본비율의 차에 대한 분산 = [0.847 * (1-0.847) / 150 ] + [0.521 * (1-0.521) / 120] = 0.0029

print(0.847 * (1-0.847) / 150  + 0.521 * (1-0.521) / 120)

표본비율의 차에 대한 정규분포

==> N ( 0.326 , 0.0029)

 

P(^p_1 - ^p_2 > 0.3) = P(Z> 0.3 - 0.326 / 루트(0.0029) ) = P(Z>= -0.48) = 0.6844

matplotlib.rc("font" , family = "Times New Roman" , weight = "bold")

X = np.arange(-5,5,.001)

fig = plt.figure(figsize=(15,8))

ax = sns.lineplot(X , scipy.stats.norm.pdf(X)) #18.31 , 3.94 어케?

X_r = round((0.3 - 0.326) / math.sqrt(0.0029),2)
area = 1- scipy.stats.norm.cdf(X_r)

ax.fill_between(X, scipy.stats.norm.pdf(X) , where = (X>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔

ax.text(-2 , .22, 'P(Z >=' + f'{X_r})'+f"\n= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(0, .2), xytext=(-2 , .2)  , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.norm.pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))

# b = [r'$\chi^2(\eta$ = {})'.format(dof)]
# print(b)
# plt.legend(b , fontsize = 15)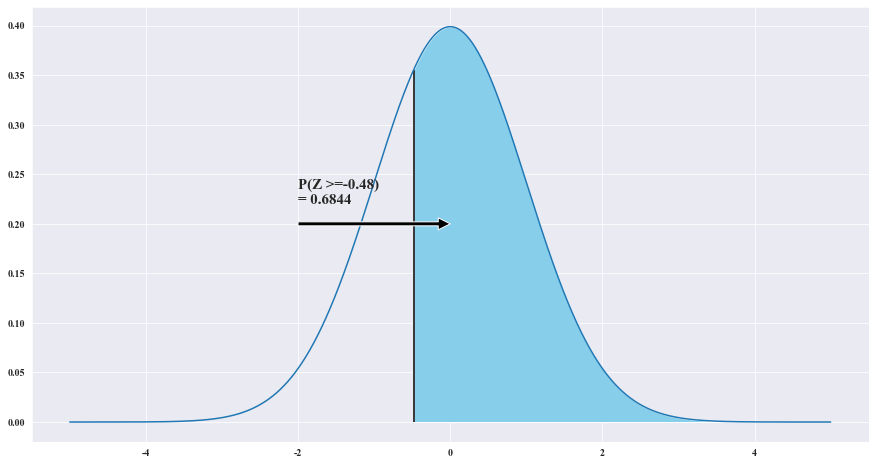

표본비율차에 대한 표본분포

EX-02) 남성 미혼 54% , 여성 미혼 36%이 K리그를 지지한다. 각각 500명씩 조사할 경우 , 지지율의 차가 10%이하일 확률

 

^p_1 = 0.54

^p_2 = 0.36

 

n = m = 500

 

P(^p1 - ^p2 <= 0.1)

 

^p_1 - ^p_2 = 0.54 - 0.36 = 0.18

 

두 표본비율의 차에대한 분산 = [0.54 * (1 - 0.54) / 500] + [0.36 * ( 1- 0.36) / 500]

print( 0.54 * (1 - 0.54) / 500 + 0.36 * ( 1- 0.36) / 500)

N(0.18 , 0.0009)

 

P(^p1 - ^p2 <= 0.1) = P(Z<=  [0.1 - 0.18 / 루트(0.0009)] ) = P(Z<= -2.67) = 0.0038

matplotlib.rc("font" , family = "Times New Roman" , weight = "bold")

X = np.arange(-5,5,.001)

fig = plt.figure(figsize=(15,8))

ax = sns.lineplot(X , scipy.stats.norm.pdf(X)) #18.31 , 3.94 어케?

X_r = round((0.1 - 0.18) / math.sqrt(0.0009),2)
area = scipy.stats.norm.cdf(X_r)

ax.fill_between(X, scipy.stats.norm.pdf(X) , where = (X<=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔

ax.text(-4 , .06, 'P(Z <=' + f'{X_r})'+f"\n= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(-3, .001), xytext=(-3 , .05)  , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.norm.pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))

# b = [r'$\chi^2(\eta$ = {})'.format(dof)]
# print(b)
# plt.legend(b , fontsize = 15)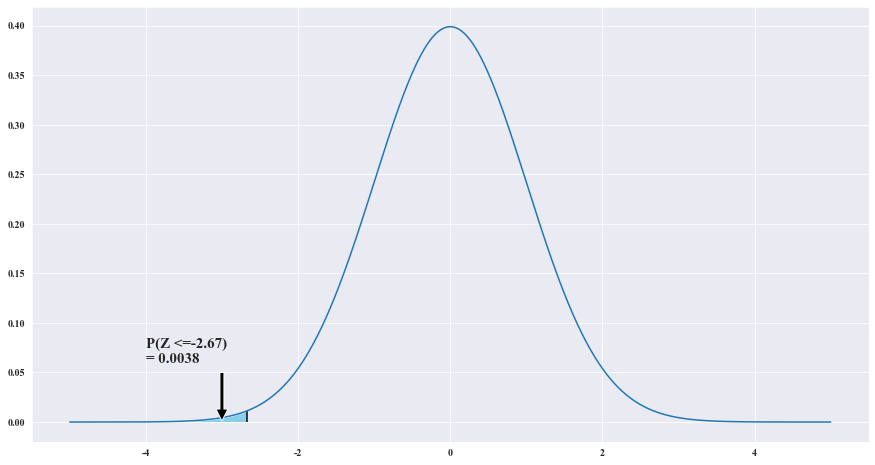

표본비율의 차에대한 표본분포

출처 :  [쉽게 배우는 생활속의 통계학]  [북스힐 , 이재원] 

※혼자 공부 정리용