이항분포에 따른 정규분포의 표준정규분포화★표본비율의 표본분포★기초통계학-[모집단 분포와 표본분포 -07]
1.표본비율의 표본분포
EX) 이항 확률변수의 실질적인 응용 ==> 여론조사 생각
==> 모집단을 구성하는 사람들의 어느 특정 사건을 선호하는 비율(p)를 알기 위하여 n명으로 구성된 표본을 임의 선정
==> n명 중 x명이 특정사건 선호
==> n명으로 구성된 표본 중에서 특정 사건을 선호하는 비율(성공률)인 표본 비율 ^p = x/n
==>개개인이 특정 사건에 대해 선호하는 비율이 독립적으로 p이므로
==> 표본으로 선정된 n명 중에서 특정 사건을 선호하는 사람의 수를 X라 하면 X~B(n, p) 이다.
https://knowallworld.tistory.com/241
이항분포식★이항실험★이항분포의 평균,분산★베르누이시행★기초통계학-[Chapter05 - 이산확률
1. 이항분포 ==> 많이 사용하는 확률 모형 : 이항분포, 푸아송분포 , 초기하분포 1. 이항실험(Bionomial Experiment) ==> 실험은 N번의 시행 ==> 실험 결과는 성공(S) , 실패(F) ==> 성공 확률 : p , 실패 확률 : q
knowallworld.tistory.com
==> X의 평균과 분산은 각각 np , npq이다.
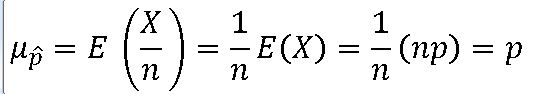
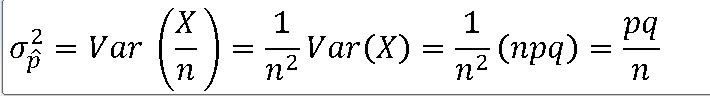
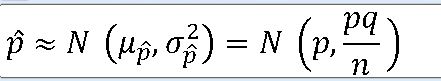
=> 표본비율 ^p의 확률분포는 평균(뮤) 과 분산(o**2)을 갖는 정규분포에 근사한다.
EX-01) 응답률 21.1%로 박지성 존경. 응답률이 전체 대학생의 생각이라는 가정아래 500명의 대학생을 임의로 선정했을 때 박지성에 대한 지지율이 25%를 넘을 확률
n = 500
p = 0.211
q = 1- 0.211 = 0.789
n = 500
p = 0.211
q = 1- 0.211
print(f'평균 : {n*p}')
print(f'분산 : {n*p*q}')표본비율의 평균 = 105.5 / 500 = 0.211
표본비율의 분산 = 83.2395 / 500**2 = 0.00033
==> 박지성에 대한 지지율을 ^p라하자.
^p ~ N(0.211 , 0.000333 )
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.25-0.211) / math.sqrt(0.000333) ,2)
#z_2 = round((200-185) / math.sqrt(900/36) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- (stats.norm.cdf(z_1))
ax.text(2.15 , .045, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.5, .017), xytext=(2.7 , .04) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))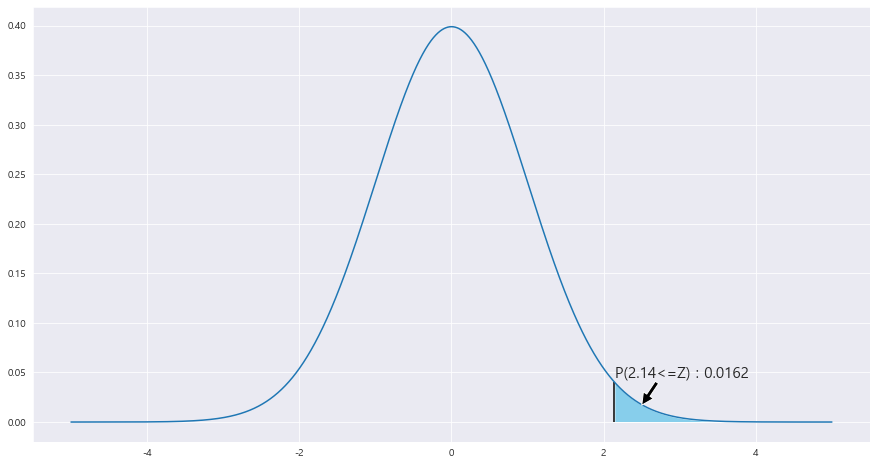
P(^p > 0.25) = P( (^p - 0.211 / 루트(0.00033) )> 0.25-0.211 / 루트(0.000332) ) = P(Z>= 2.14) = 0.0158
EX-02) 35명의 왼손잡이가 포함된 1000명의 어린이 중 무작위로 40명 선정
1> 선정된 어린이 중에서 적어도 2명의 왼손잡이가 있을 확률
https://knowallworld.tistory.com/254
정규분포의 표준정규분포로의 변환★기초통계학-[Chapter06 - 연속확률분포-03]
1. 정규분포와 표준정규분포의 관계 =========================== ==> P(z_a =2.5 , facecolor = 'skyblue') # x값 , y값 , 0 , x= 2.5) = P(Z 박테리아의 수가 75마리 이상 103마리 이하일 확률 P(75
knowallworld.tistory.com
==> 이항분포에 따른 정규분포의 표준정규분포로의 변환
n = 40
p = 35/1000 = 0.035
q = 1 - 0.035 = 0.865
40명안에 포함된 왼손잡이 어린이 수를 X라 하면 , X ~ B(40 , 0.035) 이다. X ~N(1.4 , 1.351)
E(X) = np = 1.4
V(X) = npq = 1.351
P(X > 2 ) = P(Z > 2-1.4 / 루트(1.351) ) = 0.3015
==>답지가 틀린듯?
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((2 - 1.4 ) / math.sqrt(1.351) ,2)
#z_2 = round((200-185) / math.sqrt(900/36) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- (stats.norm.cdf(z_1))
ax.text(2.15 , .045, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.5, .017), xytext=(2.7 , .04) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))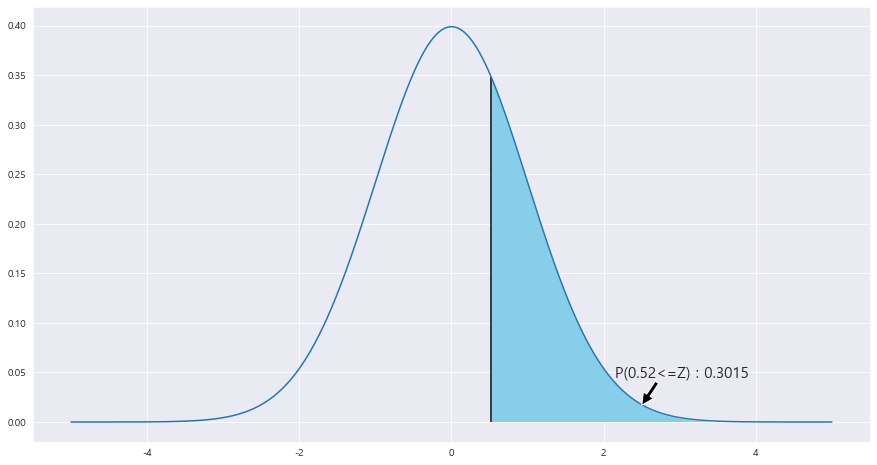
2> 선정된 어린이 중에서 왼손잡이의 비율이 5% 이상일 확률
n = 40
p = 0.035
q = 1- 0.035
print(f'평균 : {n*p / n}')
print(f'분산 : {n*p*q / n**2}')표본비율의 평균 = 40 * 0.035 / 40 = 0.035
표본비율의 분산 = 40 * 0.035 * 0.865 / 40**2 = 0.00084
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.05 - 0.035 ) / math.sqrt(0.00084) ,2)
#z_2 = round((200-185) / math.sqrt(900/36) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- (stats.norm.cdf(z_1))
ax.text(2.15 , .045, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.5, .017), xytext=(2.7 , .04) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))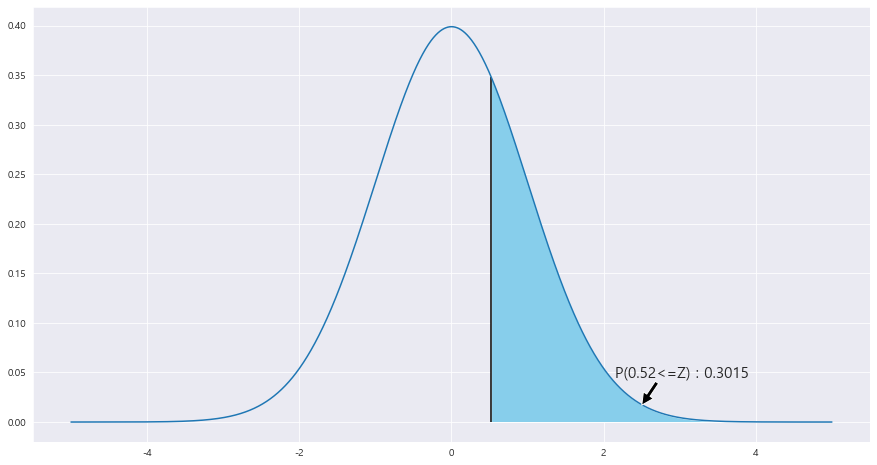
P(^p > 0.05 ) = P(Z > 0.05 - 0.035 / 루트(0.00084) ) = 1 - P( (0.05 -0.035) / 루트(0.00084)) = P(0.52<=Z) = 0.3015
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★두 표본평균의 차에 대한 표본분포(모분산 모를때)★중심극한정리 활용★이표본의 표본분포★기초통계학-[모집단 분포와 표본분포 -09] (0) | 2023.01.06 |
|---|---|
| ★두 표본평균의 차에 대한 표본분포(모분산 알때 , 동일할때)★중심극한정리 활용★이표본의 표본분포★기초통계학-[모집단 분포와 표본분포 -08] (0) | 2023.01.06 |
| ★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집단 분포와 표본분포 -06] (0) | 2023.01.06 |
| ★중심극한정리★기초통계학-[모집단 분포와 표본분포 -05] (0) | 2023.01.06 |
| ★lineplot★중심극한정리★기초통계학-[모집단 분포와 표본분포 -04] (0) | 2023.01.05 |