전체 글
-
★표본비율의 차에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -12]2023.01.07
★확률질량함수의 평균 분산★그룹화자료의 평균과 분산이 아닌 확률질량함수이다!!!★이산균등분포★기초통계학-[연습문제01 -13]
1. 모집단분포가 이산균등분포 X ~ DU(6)인 모집단으로부터 크기 2인 표본을 임의 추출
==> 이산균등분포
1> 표본으로 나올 수 있는 모든 경우의 수
==> 복원추출에 의한 2개씩 뽑는다.
A = list(itertools.product(np.arange(1,7) , repeat = 2))
A[(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1),
(3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)]
2> 각 표본의 평균
각 표본의 평균 : [1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, 3.5, 4.0, 4.5, 5.0, 5.5, 6.0]
표본들의 평균 :[1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, 6.0]
3> 표본평균 |X의 확률분포
a = list(itertools.product(np.arange(1,7) , repeat = 2))
# print(a)
b = list(map(lambda x : np.mean(x) , a))
d = deque()
for i in zip(a,b):
d.append(i)
c = sorted(list(set(list(map(lambda x : np.mean(x) , a)))))
d = deque(sorted(d , key = lambda x : x[1]))
e =[[] for i in range(len(c))]
# print(type(d))
# print(len(a))
p=0
while len(d)>=2:
if d[0][1] == d[1][1]:
e[p].append(d[0][0])
# print(f'e: {e}')
d.popleft()
# print(f'd: {d}')
else:
e[p].append(d[0][0])
# print(f'일치 x e: {e}')
d.popleft()
p+=1
e[p].append(d[-1][0])
B = pd.DataFrame([e ,c]).T
B.rename(columns= {0 : '표본' , 1: '|X'} , inplace = True)
B
b_len = [len(i) for i in B['표본']]
b_len
B['표본길이'] = b_len
B['P(|X = x)'] = B['표본길이'] / len(a)
B['평균'] = B['|X'] * B['P(|X = x)']
B['분산'] = (B['|X']**2) * B['P(|X = x)']
a = pd.DataFrame(B[:].sum(axis=0))
# a.transpose()
a = a.transpose()
col_name = a.columns.tolist()
for i in range(len(col_name[:-3])):
a.iloc[0][i] = '-'
a.iloc[0][3] = '결과값'
a.iloc[0][5] = a.iloc[0][5] - a.iloc[0][4]**2
B = pd.concat([B ,a])
B
B.iloc[:-1, [1,3]]
4> 표본평균 |X의 평균과 분산
평균 : 3.5
분산 : 1.45833
np.var(각 표본들의 평균 , ddof=0) ==> 모분산
5> 모집단분포의 평균과 분산을 구하라.
x = 1, 2, 3, 4, 5, 6


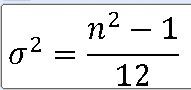
https://knowallworld.tistory.com/245
★초기하분포★기하분포★이산균등분포★기초통계학-[Chapter05 - 이산확률분포-06]
1. 이산균등분포(Discrete Uniform Distribution) 1> 동전을 한 번 던져서 앞면이 나온 횟수를 X ==> p(x) = 1/2 , x= 0 ,1 2> 주사위를 한 번 던질 때 나온 눈의 수를 확률 변수 X라 하면 ==> p(x) = 1/6 , x =1 , 2, 3, 4, 5,
knowallworld.tistory.com
평균 : (1 + 6) / 2 = 3.5
분산 : (6**2 -1) / 12 = 2.9217
2. 모집단의 확률분포가 p(1) = 0.8 , p(2) = 0.2 인 양의 비대칭일 때, 이 모집단으로부터 크기 2인 표본을 임의로 추출한다.
https://knowallworld.tistory.com/241
이항분포식★이항실험★이항분포의 평균,분산★베르누이시행★기초통계학-[Chapter05 - 이산확률
1. 이항분포 ==> 많이 사용하는 확률 모형 : 이항분포, 푸아송분포 , 초기하분포 1. 이항실험(Bionomial Experiment) ==> 실험은 N번의 시행 ==> 실험 결과는 성공(S) , 실패(F) ==> 성공 확률 : p , 실패 확률 : q
knowallworld.tistory.com
==> 성공확률 0.8인 이항분포식 ==> but. 이항분포식은 횟수가 지정되어야 한다.

https://knowallworld.tistory.com/218
insert() , index★그룹화 자료의 분산과 표준편차★기초통계학-[Chapter03 - 07]
1. 그룹화 자료의 분산과 표준편차 A ='29 30 49 21 39 38 15 39 48 41 50 38 33 40 51 29 31 42 29 69 37 20 49 40 10 49 49 49 35 45 22 45 20 45 30 41 40 38 10 31 47 19 31 21 41 46 28 29 18 28' A = list(map(int, A.split(' '))) A A = [29, 30, 49, 21,
knowallworld.tistory.com
==> 그룹화 자료의 분산
https://knowallworld.tistory.com/240
표본,모표본★평균과 분산★기초통계학-[Chapter05 - 이산확률분포-02]
1. 평균 ==> 이산확률변수의 확률 히스토그램 ==> 상대도수히스토그램과 유사 But. 상대도수히스토그램은 n개의 자료 값에 대한 표본 설명 확률 히스토그램은 실험에서 발생할 수 있는 모든 경우에
knowallworld.tistory.com
==> 이 문제는 확률질량함수 이다!!!!!!!!!!!!!!!!!!!!!!!!!
1> 표본으로 나올 수 있는 모든 경우의 수
x = 1, 2
모든 경우의 수 : [(1, 1), (1, 2), (2, 1), (2, 2)]
2> 각표본의 평균
각 표본별 평균 : [1.0, 1.5, 1.5, 2.0]
표본들의 평균 : [1.0 , 1.5 , 2.0]
==> 계급값이라고 생각하자!!!
3> 표본평균 |X의 확률분포를 구하라.
# print(a)
b = list(map(lambda x : np.mean(x) , a))
d = deque()
for i in zip(a,b):
d.append(i)
c = sorted(list(set(list(map(lambda x : np.mean(x) , a)))))
d = deque(sorted(d , key = lambda x : x[1]))
e =[[] for i in range(len(c))]
# print(type(d))
# print(len(a))
p=0
while len(d)>=2:
if d[0][1] == d[1][1]:
e[p].append(d[0][0])
# print(f'e: {e}')
d.popleft()
# print(f'd: {d}')
else:
e[p].append(d[0][0])
# print(f'일치 x e: {e}')
d.popleft()
p+=1
e[p].append(d[-1][0])
B = pd.DataFrame([e ,c]).T
B.rename(columns= {0 : '표본' , 1: '|X'} , inplace = True)
b_len = [len(i) for i in B['표본']]
b_len
B['표본길이'] = b_len
B
P_X = [(0.8** i[0].count(1) * 0.2**i[0].count(2) * len(i)) for i in B['표본']]
B['P(|X = x)'] = P_X
B['평균'] = B['|X'] * B['P(|X = x)']
B['분산'] = (B['|X']**2) * B['P(|X = x)']
a = pd.DataFrame(B[:].sum(axis=0))
# a.transpose()
a = a.transpose()
col_name = a.columns.tolist()
for i in range(len(col_name[:-3])):
a.iloc[0][i] = '-'
a.iloc[0][3] = '결과값'
a.iloc[0][5] = a.iloc[0][5] - a.iloc[0][4]**2 #분산 = |X**2 * P(X) - 평균**2
B = pd.concat([B ,a])
B
P_X = [(0.8** i[0].count(1) * 0.2**i[0].count(2) * len(i)) for i in B['표본']]==> 확률 P(|X = x)
B.iloc[:-1 , [1,3]]
|X = 1 , 0.8*0.8 = 0.64
|X = 2 , 0.8*0.2 *2 = 0.16 *2 = 0.32
|X = 3 , 0.2 *0.2 = 0.04
4> 표본평균 |X의 평균과 분산을 구하라.
평균 : 1.2
분산 : 0.08( |X**2 - P(X) - 평균의 제곱)
5>모집단분포의 평균과 분산을 구하라.



평균 : 1*0.8 + 2*0.2 = 0.8 + 0.4 = 1.2
분산 : [(1-1.2)**2]*0.8 + [(2-1.2)**2]*0.2 = 0.16
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★Solve()이후 float로의 변환★크기를 알때/모를때의 표본평균의 표준분포★기초통계학-[연습문제02 -15] (0) | 2023.01.09 |
|---|---|
| ★표본평균의 정규분포(표본평균 = 모평균 , 표본분산 = 모분산/크기)★모분산 모를때 정규표본 추출★기초통계학-[연습문제02 -14] (0) | 2023.01.09 |
| ★표본비율의 차에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -12] (0) | 2023.01.07 |
| ★F-분포★두 표본분산의 비에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -11] (1) | 2023.01.07 |
| ★서로독립인 정규집단의 표본분산(모분산은 알때) 추론★카이제곱분포★합동표본분산에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -10] (0) | 2023.01.07 |
★표본비율의 차에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -12]
1. 두 표본비율의 차에 대한 표본분포
==> 서로 독립이고 모비율이 각각 p_1 , p_2인 두 모집단에서 각각 크기 n,m인 표본 선정
==> 표본의 크기가 충분히 크다면
https://knowallworld.tistory.com/301
★모비율★표본비율★기초통계학-[모집단 분포와 표본분포 -02]
1. 모비율(Population Proportion) ==> 모집단을 형성하고 있는 모든 대상에 대한 특정한 성질을 갖고 있는 대상의 비율(p)를 나타낸다. 2. 표본비율(Sample Proportion) ==> 확률분포를 이루는 대상에 대한 특정
knowallworld.tistory.com
https://knowallworld.tistory.com/306
이항분포에 따른 정규분포의 표준정규분포화★표본비율의 표본분포★기초통계학-[모집단 분포
1.표본비율의 표본분포 EX) 이항 확률변수의 실질적인 응용 ==> 여론조사 생각 ==> 모집단을 구성하는 사람들의 어느 특정 사건을 선호하는 비율(p)를 알기 위하여 n명으로 구성된 표본을 임의 선정
knowallworld.tistory.com
==> 표본비율의 표본분포의 정규분포 근사


EX-01) 무죄를 주장하는 피고인이 교도소로 보내지는 비율은 84.7% , 유죄를 인정하는 피고인 중에 교도소로 보내지는 비율은 52.1%. 무죄를 주장하는 피고인 150명과 유죄를 인정하는 피고인 120명 선정. 무죄를 주장하는 피고인 중에 교도소로 보내지는 비율을 ^p , 유죄를 인정하는 피고인 중에 교도소로 보내지는 비율을 ^p_2 라 할때 ^p_1 - ^p_2가 30%를 초과할 확률
무죄 주장 ==> 교도소 갈 확률 ==> ^p_1 = 0.847
유죄 주장 ==> 교도소 갈 확률 ==> ^p_2 = 0.521
n = 150
m= 120
^p_1 - ^p_2 = 0.847 - 0.521 = 0.326
표본비율의 차에 대한 분산 = [0.847 * (1-0.847) / 150 ] + [0.521 * (1-0.521) / 120] = 0.0029
print(0.847 * (1-0.847) / 150 + 0.521 * (1-0.521) / 120)표본비율의 차에 대한 정규분포
==> N ( 0.326 , 0.0029)
P(^p_1 - ^p_2 > 0.3) = P(Z> 0.3 - 0.326 / 루트(0.0029) ) = P(Z>= -0.48) = 0.6844
matplotlib.rc("font" , family = "Times New Roman" , weight = "bold")
X = np.arange(-5,5,.001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(X , scipy.stats.norm.pdf(X)) #18.31 , 3.94 어케?
X_r = round((0.3 - 0.326) / math.sqrt(0.0029),2)
area = 1- scipy.stats.norm.cdf(X_r)
ax.fill_between(X, scipy.stats.norm.pdf(X) , where = (X>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
ax.text(-2 , .22, 'P(Z >=' + f'{X_r})'+f"\n= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(0, .2), xytext=(-2 , .2) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.norm.pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
# b = [r'$\chi^2(\eta$ = {})'.format(dof)]
# print(b)
# plt.legend(b , fontsize = 15)
EX-02) 남성 미혼 54% , 여성 미혼 36%이 K리그를 지지한다. 각각 500명씩 조사할 경우 , 지지율의 차가 10%이하일 확률
^p_1 = 0.54
^p_2 = 0.36
n = m = 500
P(^p1 - ^p2 <= 0.1)
^p_1 - ^p_2 = 0.54 - 0.36 = 0.18
두 표본비율의 차에대한 분산 = [0.54 * (1 - 0.54) / 500] + [0.36 * ( 1- 0.36) / 500]
print( 0.54 * (1 - 0.54) / 500 + 0.36 * ( 1- 0.36) / 500)N(0.18 , 0.0009)
P(^p1 - ^p2 <= 0.1) = P(Z<= [0.1 - 0.18 / 루트(0.0009)] ) = P(Z<= -2.67) = 0.0038
matplotlib.rc("font" , family = "Times New Roman" , weight = "bold")
X = np.arange(-5,5,.001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(X , scipy.stats.norm.pdf(X)) #18.31 , 3.94 어케?
X_r = round((0.1 - 0.18) / math.sqrt(0.0009),2)
area = scipy.stats.norm.cdf(X_r)
ax.fill_between(X, scipy.stats.norm.pdf(X) , where = (X<=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
ax.text(-4 , .06, 'P(Z <=' + f'{X_r})'+f"\n= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(-3, .001), xytext=(-3 , .05) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.norm.pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
# b = [r'$\chi^2(\eta$ = {})'.format(dof)]
# print(b)
# plt.legend(b , fontsize = 15)
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
★F-분포★두 표본분산의 비에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -11]
1. 두 표본분산의 비에 대한 표본분포
==> 서로 독립인 두 정규모집단의 모분산이 다를때, 모분산 중에서 어느 것이 더큰지 비교하는 경우
==> 모분산은 양수이므로, 두 모분산의 비의 값을 이용하여 비교가능

https://knowallworld.tistory.com/260
★scipy.stats.f(자유도1 , 자유도 2).pdf()★F-분포★기초통계학-[Chapter06 - 연속확률분포-08]
1. F-분포(F-distribution) ==> 서로 독립인 두 모집단의 모분산이 동일한지 아닌지를 통계적으로 추론 ==> 서로 독립인 두 확률변수 F ~ F(m , n) X = np.arange(0,10, .01) fig = plt.figure(figsize = (15,8)) dof = [[5,8] , [2
knowallworld.tistory.com
==> F-분포
==> 서로 독립인 두 모집단의 모분산이 동일한지 아닌지를 통계적으로 추론
==> 모분산 동일하지 않을 때 표본분포 값 구한다.
https://knowallworld.tistory.com/305
★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집
1. 모분산의 표본분포 정규모집단 N(뮤 , 모분산) 으로부터 크기 n인 표본을 선정할 때 표본분산 ==> 표본분산 S**2에 대한 표본분포는 X**2-통계량 V에 대하여 자유도가 n-1인 카이제곱분포이다. https:
knowallworld.tistory.com

EX-01) 서로 독립인 두 정규모집단 N(뮤_1 , 9)와 N(뮤_2 , 8)에서 각각 크기 5와 6인 확률표본 추출, 이때
P( [S_1**2 / S_2**2] > s_0 ) = 0.05를 만족하는 s_0를 구하라.
n = 5
m = 6
자유도_1 = 5 -1 =4
자유도_2 = 6 -1 = 5
분산_1 = 9
분산_2 = 8
(S_1**2 / 9 ) / (S_2**2 / 8) ~ F(4,5)
X = np.arange(0,10, .01)
fig = plt.figure(figsize = (15,8))
dof = [[4,5]]
#print(dof[0][0])
for i in dof:
ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
b = ['F({},{})'.format(i,j) for i,j in dof]
X_r = scipy.stats.f(dof[0][0], dof[0][1]).ppf(0.95)
X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(0.05)
ax.fill_between(X, scipy.stats.f(dof[0][0],dof[0][1]).pdf(X) , where = (X>=X_r) | (X<=X_l) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
ax.vlines(X_r , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_r) , color = 'black')
ax.vlines(X_l , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_l) , color = 'black')
ax.annotate('' , xy=(X_l -0.02 , 0.1) , xytext=(X_l + 0.5 , 0.1) , arrowprops = dict(facecolor = 'black'))
ax.text(X_l + 0.5 , 0.1 , r'$P(F\leqq f_{0.95,4,5})$' + f'= {0.05}' , fontsize = 14)
ax.annotate('' , xy=(X_r +0.3 , 0.01) , xytext=(X_r + 0.3 , 0.2) , arrowprops = dict(facecolor = 'black'))
ax.text(X_r + 0.3 , 0.21 , r'$P(F\geqq f_{0.05,4,5})$' + f'= {0.05}' , fontsize = 14)
ax.text(X_l + 0.05 , 0.01 , r'$f_{0.95,4,5}$)' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(0.05) ,2)}' ,fontsize = 13)
ax.text(X_r - 1.3 , 0.01 , r'$f_{0.05,4,5}$)' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(0.95) , 2)}' ,fontsize = 13)
plt.legend(b , fontsize= 15)
P(S_1**2 / S_2**2 > s_0 ) = P( [8 * S_1**2] / [9 *S_2**2] > (8/9)*s_0 ) = P(F > (8/9)*s_0 ) = 0.05
s_0 = 5.19* (9/8) = 5.838
EX-02) 동일한 모분산을 갖는 서로 독립인 두 정규모집단에서 각각 크기 10과 15인 확률표본 추출, 이때
P( [S_1**2 / S_2**2] > s_0 ) = 0.025를 만족하는 s_0를 구하라.
모분산_1 = 모분산_2
n = 10
m = 15
자유도_1 = 10-1 = 9
자유도_2 = 15-1 = 14
P(F > s_0) = 0.025
X = np.arange(0,10, .01)
fig = plt.figure(figsize = (15,8))
dof = [[9,14]]
#print(dof[0][0])
for i in dof:
ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
b = ['F({},{})'.format(i,j) for i,j in dof]
X_r = scipy.stats.f(dof[0][0], dof[0][1]).ppf(1-0.025)
X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(0.025)
ax.fill_between(X, scipy.stats.f(dof[0][0],dof[0][1]).pdf(X) , where = (X>=X_r) | (X<=X_l) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
ax.vlines(X_r , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_r) , color = 'black')
ax.vlines(X_l , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_l) , color = 'black')
ax.annotate('' , xy=(X_l -0.02 , 0.1) , xytext=(X_l + 0.5 , 0.1) , arrowprops = dict(facecolor = 'black'))
ax.text(X_l + 0.5 , 0.1 , r'$P(F\leqq f_{0.975,9,14})$' + f'= {0.025}' , fontsize = 14)
ax.annotate('' , xy=(X_r +0.3 , 0.01) , xytext=(X_r + 0.3 , 0.2) , arrowprops = dict(facecolor = 'black'))
ax.text(X_r + 0.3 , 0.21 , r'$P(F\geqq f_{0.025,9,14})$' + f'= {0.025}' , fontsize = 14)
ax.text(X_l + 0.05 , 0.01 , r'$f_{0.975,9,14}$' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(X_l) ,2)}' ,fontsize = 13)
ax.text(X_r - 1.3 , 0.01 , r'$f_{0.025,9,14}$' + f'= {round(X_r , 2)}' ,fontsize = 13)
plt.legend(b , fontsize= 15)
s_0 = 3.21
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
1. 합동표본분산에 대한 표본분포

==> 동일한 모분산을 갖는 서로 독립인 두 정규 모집단
==> 크기가 n과 m인 두 확률표본 추출
==>두 표본의 표본분산에 대한 합동표본분산 정의

https://knowallworld.tistory.com/258
★scipy.stats.chi2().ppf()★matplotlib 수학식표현★카이제곱분포★정규분포★기초통계학-[Chapter06 - 연
1. 카이제곱분포 ==> 카이제곱분포는 정규모집단의 모분산에 대한 통계적 추론에 사용 ==> n개의 서로 독립인 표준정규확률변수 Z_1 ,Z_2 ,···· Z_n 에 대하여 확률변수의 확률분포를 자유도(degree of
knowallworld.tistory.com
==> 카이제곱분포는 정규모집단의 모분산에 대한 통계적 추론에 사용
EX-01) 서로 독립인 두 정규모집단 N(뮤_1 , 25)와 N(뮤_2 , 25)에서 각각 크기 8,10인 확률 표본을 추출
P(S_p**2 >s_0) = 0.05를 만족하는 s_0을 구하라
모분산 1 = 모분산 2 = 25
n = 8
m= 10
n+m-2 / 모분산 = 16 / 25
자유도 = n+m-2 = 16
16/25 * S_p ~ x**2(16)
matplotlib.rc("font" , family = "Times New Roman" , weight = "bold")
X = np.arange(0,30,.01)
fig = plt.figure(figsize=(15,8))
dof = 16 #자유도
ax = sns.lineplot(X , scipy.stats.chi2(dof).pdf(X)) #18.31 , 3.94 어케?
#P(X>X_r) = 0.05
#P(X<=X_r) = 0.95
X_r = scipy.stats.chi2(dof).ppf(0.95)
#X_r = 10 + math.sqrt(20)*1.644 #평균 = n , 분산 = 2n
print(X_r)
ax.fill_between(X, scipy.stats.chi2(dof).pdf(X) , where = (X>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = 1- scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(27 , .025, 'P(X >=' + r'$\chi^2_{0.05}$)' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(27, .005), xytext=(27 , .02) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 3.5, .01, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
b = [r'$\chi^2(\eta$ = {})'.format(dof)]
print(b)
plt.legend(b , fontsize = 15)
==> 자유도 16에 대한 백분위수 95% x_0.05**2 = 26.3
P(S_p**2 > s_0) = P(16/25 * S_p**2 > 16/25 * s_0) = P(X > X_R**2 )
16/25 * s_0 = 26.3
print(26.3 * 25 / 16)s_0 = 26.3 * 25 / 16 = 41.094
EX-02) 서로 독립인 두 정규모집단 N(24 , 16)과 N(28 , 16)에서 각각 크기 10,15인 확률 표본을 추출
P(S_p**2 >s_0) = 0.05를 만족하는 s_0을 구하라
모분산_1 = 모분산_2 = 16
뮤_1 = 24
뮤_2 = 16
n = 10
m = 15
자유도 = n+m-2 = 10+15 - 2 = 23
23/16*S_p**2 ~ X**2(16)
matplotlib.rc("font" , family = "Times New Roman" , weight = "bold")
X = np.arange(0,50,.01)
fig = plt.figure(figsize=(15,8))
dof = 23 #자유도
ax = sns.lineplot(X , scipy.stats.chi2(dof).pdf(X)) #18.31 , 3.94 어케?
#P(X>X_r) = 0.05
#P(X<=X_r) = 0.95
X_r = scipy.stats.chi2(dof).ppf(0.95)
#X_r = 10 + math.sqrt(20)*1.644 #평균 = n , 분산 = 2n
print(X_r)
ax.fill_between(X, scipy.stats.chi2(dof).pdf(X) , where = (X>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = 1- scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(37, .025, 'P(X >=' + r'$\chi^2_{0.05}$)' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(37, .005), xytext=(37 , .02) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 6.5, .01, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
b = [r'$\chi^2(\eta$ = {})'.format(dof)]
print(b)
plt.legend(b , fontsize = 15)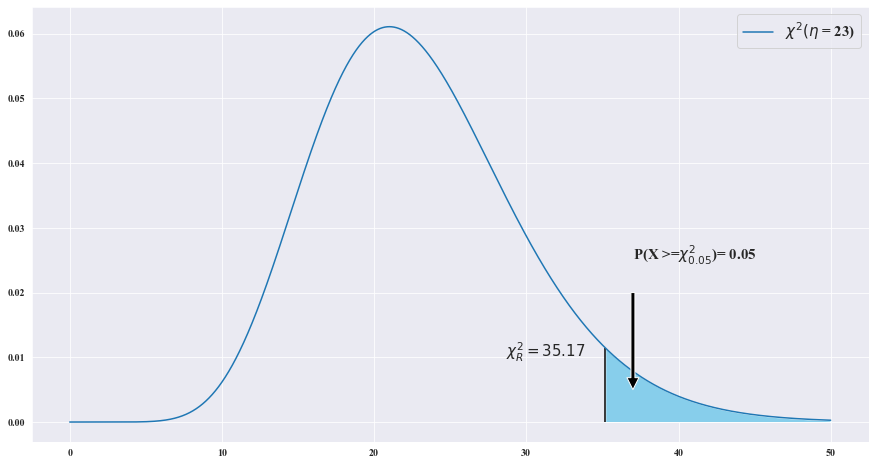
P(S_p**2 > s_0) =P( 23/16* S_p**2 > 23/16*s_0 ) = P(X > X_R**2)
s_0 = 16/23 * 35.17 = 24.46
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★표본비율의 차에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -12] (0) | 2023.01.07 |
|---|---|
| ★F-분포★두 표본분산의 비에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -11] (1) | 2023.01.07 |
| ★두 표본평균의 차에 대한 표본분포(모분산 모를때)★중심극한정리 활용★이표본의 표본분포★기초통계학-[모집단 분포와 표본분포 -09] (0) | 2023.01.06 |
| ★두 표본평균의 차에 대한 표본분포(모분산 알때 , 동일할때)★중심극한정리 활용★이표본의 표본분포★기초통계학-[모집단 분포와 표본분포 -08] (0) | 2023.01.06 |
| 이항분포에 따른 정규분포의 표준정규분포화★표본비율의 표본분포★기초통계학-[모집단 분포와 표본분포 -07] (0) | 2023.01.06 |
1. 두 표본평균의 차에 대한 표본분포(두 모분산을 모르는 경우)
https://knowallworld.tistory.com/302
★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본
1. 표본평균의 표본분포(모분산을 아는 경우) ==> 표본평균에 대한 표본분포는 정규분포를 따른다. EX-01) 모평균 100 , 모분산 9인 정규모집단으로부터 크기 25인 표본을 임의로 추출 1> 표본평균 |X
knowallworld.tistory.com
==> 대부분 모집단의 모분산이 알려지지 않는다.
==> 단일 표본에 대한 표본평균은 t-분포와 관련되는 것을 알 수 있다.
==> 이 표본인 경우에도 두 표본평균의 차는 t-분포를 사용한다.
이표본의 t-분포에 대한 특징
㉠ 두 모집단분포는 정규분포이다.
㉡ 두 모분산은 알려지지 않았으나 동일하다.
㉢ 두 표본분산을 공동으로 사용한다.
==> 합동표본분산(Pooled sample Variance)


==> 실제로 모분산이 알려지지 않으므로, 공동으로 사용하는 표본표준편차로 대치한다.
==> 서로 독립인 집단에서 공동으로 사용한다는 의미
==> 미지의 동일한 모분산을 가지는 서로 독립인 두 정규 모집단에서 각각 크기가 n과 m인 두 확률표본을 추출할때, 두 표본평균의 차 |X - |Y는 자유도 n+m-2 인 t-분포를 따른다.
https://knowallworld.tistory.com/259
★scipy.stats.t(자유도).ppf()★t-분포★기초통계학-[Chapter06 - 연속확률분포-07]
1. T-분포(Chi-square Distribution) ==> T-분포는 모분산이 알려지지 않은 정규모집단의 모평균에 대한 추론 ==>서로 독립인 표준정규화확률변수 Z와 자유도 n인 카이제곱 확률변수 V에 대하여 정의 ==> T ~
knowallworld.tistory.com
EX-01) 타이어의 공정방법에 따른 예전 방법과 새로운 방법으로 생산한 타이어의 수명 차이를 알아본다.
평균 수명이 동일하고, 표본평균은 새로 생산한 타이어가 예전 방식으로 생산한거 보다 1.518km이상 더클 확률(두 독립집단은 동일한 분산을 갖는 정규분포를 따른다.)
새로운방법 : [65.4 , 63.6 , 61.5 , 62.6 , 61.1 , 60.4 , 62.5 , 62.4 , 63.7]
예전 방법 : [59.2 , 60.6 , 56.2 , 62.0 , 58.1 , 57.7 , 58.1]
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
#%%
new = [65.4 , 63.6 , 61.5 , 62.6 , 61.1 , 60.4 , 62.5 , 62.4 , 63.7]
old = [59.2 , 60.6 , 56.2 , 62.0 , 58.1 , 57.7 , 58.1]
print(f'new 평균 : {np.mean(new)}')
print(f'new 분산 : {np.var(new , ddof = 1)}')
print(f'old 평균 : {np.mean(old)}')
print(f'old 분산 : {np.var(old , ddof=1)}')새로운 타이어의 표본평균 : 62.57
새로운 타이어의 표본분산 : 2.3
n = 9
옛날 타이어의 표본평균 : 58.84
옛날 타이어의 표본분산 : 3.762
m = 7
==> 합동표본분산
s_p**2 = 1/(9+7-2) * [(9-1)*2.3 + (7-1) * 3.762] = 2.926
s_p = 1.71
s_|x-|y = s_p * 루트( (1/n) + (1/m) ) = 1.71 * 루트( (1/9) + (1/7) ) = 0.8617
자유도 = n+m-2
|X - |Y는 자유도 14인 t-분포를 따른다.
P( (|X-|Y) > 1.518 )
U = |X - |Y
뮤_x - 뮤_y = 0
s = 0.8617
P(U > 1.518) = P(T > 1.518 - 0 / 0.8617) = P(T>= 1.76) = 0.05
X = np.arange(-5,5 , .01)
fig = plt.figure(figsize=(15,8))
dof_2 = [14] #자유도
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
#t_r = scipy.stats.t(dof_2).ppf(1- 0.05)
t_r = 1.76
print(t_r)
area = round(float(1- scipy.stats.t(dof_2).cdf(1.76)),2)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
plt.annotate('' , xy=(3.0, .007), xytext=(2.5 , .16) , arrowprops = dict(facecolor = 'black'))
ax.text(1.71 , .17, r'$P(T>t_{0.05})$' + f'= {area}',fontsize=15)
ax.text(t_r - 0.8 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
EX-02) 자동차 공정라인에 따른 평균 시간 차이 여부 파악. 공정라인 A의 표본평균이 공장라인 B의 표본평균보다 1.66분 이상일 확률(엔진을 올리는 시간을 정규분포를 따르고, 단위는 분)
공정라인 A: [3 , 7 , 5 , 8 , 4 , 3]
공정라인 B : [2 , 4 , 9 , 3, 2]
A = [3 , 7 , 5 , 8 , 4 , 3]
B = [2 , 4 , 9 , 3, 2]
print(f'A 평균 : {np.mean(A)}')
print(f'A 분산 : {np.var(A , ddof = 1)}')
print(f'B 평균 : {np.mean(B)}')
print(f'B 분산 : {np.var(B , ddof=1)}')A의 평균 : 5
A의 분산 : 4.4
n = 6
B의 평균: 4
B의 분산 : 8.5
m = 5
VARS = (1/9) * ((5 *4.4) + (4*8.5))
STDS = math.sqrt(VARS)
print(VARS)
print(STDS)s_p**2 = (1 / (n+m-2) ) * [ (n-1) * s_A**2 ) + (m-1) * s_B**2 ) ] = (1/9) * [(5 * 4.4) + (4 * 8.5) ] = 6.22
s_p = 2.494
print(STDS * math.sqrt( (1/6) + (1/5)))S = s_p * (루트 ( (1/6) + (1/5) ) = 1.51
뮤_|x = 뮤_|y
뮤_|x - 뮤_|y = 0
자유도 = n + m - 2 = 9
P(|X - |Y >= 1.66) = P(T >= (1.66 -0) / 1.51 ) = 0.15
X = np.arange(-5,5 , .01)
fig = plt.figure(figsize=(15,8))
dof_2 = [9] #자유도
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
#t_r = scipy.stats.t(dof_2).ppf(1- 0.05)
t_r = round(1.66 / 1.51 ,2)
print(t_r)
print(scipy.stats.t(dof_2).ppf(0.85))
area = round(float(1- scipy.stats.t(dof_2).cdf(t_r)),2)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
plt.annotate('' , xy=(3.0, .007), xytext=(2.5 , .16) , arrowprops = dict(facecolor = 'black'))
ax.text(1.71 , .17, r'$P(T>t_{0.15})$' + f'= {area}',fontsize=15)
ax.text(t_r - 0.8 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
==> t_0.15 ==> 꼬리확률 15% , t_0.15 = 0.15
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
1. 이표본의 표본분포
==>지금까지는 단일 모집단의 표본에 대한 통계량의 표본분포
EX) 수능에서 남학생, 여학생 집단의 평균이 동일한지 여부 비교
==> 비교위해서는 각각 표본을 추출하여야 한다.
==> 서로 독립인 두 모집단의 모수를 비교하기 위해서는 각각 표본을 추출하고, 두 표본으로부터 적당한 통계량을 산출해야한다.
2. 두 표본평균의 차에 대한 표본분포(두 모분산을 아는 경우)
==> 두 모분산을 알고 있고, 서로 독립인 정규모집단 N(뮤_1 , o_1**2) , N(뮤_2 , o_2**2) 로부터 각각 n과 m인 표본을 추출했을 때, 각각의 표본평균을 |X, |Y라 하자.
https://knowallworld.tistory.com/302
★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본
1. 표본평균의 표본분포(모분산을 아는 경우) ==> 표본평균에 대한 표본분포는 정규분포를 따른다. EX-01) 모평균 100 , 모분산 9인 정규모집단으로부터 크기 25인 표본을 임의로 추출 1> 표본평균 |X
knowallworld.tistory.com
==> 표본평균 : N(뮤_1 , o_1**2 / n) , N (뮤_2 , o_2**2 / m)


EX-01) 모분산이 각각 9 , 16이고 동일한 모 평균을 갖는 서로 독립인 두 정규모집단에서 각각 크기가 n=m = 64인 표본을 추출하였다. 첫 번째 모집단의 표본평균을 |X , 두번째 모집단의 표본평균을 |Y라 할때 | |X - |Y | 가 2보다 클 확률
==> 표본평균 N( |X , 9) , N( |Y , 16)
==> |X - |Y의 분산 = 9/ 64 + 16/64 = 25 /64
==> U = |X - |Y라하면 U ~ N(0, 25/64)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((-2-0) / math.sqrt(25/64) ,2)
z_2 = round((2-0) / math.sqrt(25/64) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_2) & (x<= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area_1 = 1 - stats.norm.cdf(z_2)
area_2 = stats.norm.cdf(z_1)
ax.text(2.71 , .034, f'P({z_2}<=Z) : {round(area_1,4)}',fontsize=15)
plt.annotate('' , xy=(3.3, .0017), xytext=(3.5 , .03) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(-3.71 , .034, f'P(Z<={z_1}) : {round(area_2,4)}',fontsize=15)
plt.annotate('' , xy=(-3.3, .0017), xytext=(-3.5 , .03) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
P(| |X- |Y | >=2 ) = P( U>=2) + P(U<=-2) = P( Z>= (2 -0) / 루트(25/64) ) + P( Z<= -2 -0 / 루트(25/64) ) = 1 - P( Z<= (2 -0) / 루트(25/64) ) + P( Z<= -2 -0 / 루트(25/64) ) = 0.0007 + 0.0007 = 0.0014
EX-02) 모평균과 모분산이 각각 뮤_1 = 5 , 뮤_2 = 4 , 분산_1 = 9 , 분산_2 = 16 , 서로 독립인 두 정규모집단에서 각각 크기 n=m=100인 표본을 추출하였다. 첫 번째 모집단의 표본평균을 |X , 두번째 모집단의 표본평균을 |Y라 할때,
| |X - |Y | 가 2보다 작을 확률을 구하라.
U = |X - |Y
U의 평균 = 5- 4 = 1
U의 분산 = 9/100 + 16/100 = 25 /100
U ~ N(1 , 25/100)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((2-1) / math.sqrt(25/100) ,2)
# z_2 = round((2-0) / math.sqrt(25/64) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=-z_1) & (x<= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area_1 = ( stats.norm.cdf(z_1) - stats.norm.cdf(0) ) * 2
ax.text(2.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area_1,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(2.5 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
P(|U| <2) = P(-2< U < 2) = (P(U<2) - P(U<0) ) * 2 = (P(Z< (2-1) / 루트(25/100)) - 0.5) * 2 = P(-2 <= Z <= 2) = 0.9545
3. 두 표본평균의 차에 대한 표본분포(두 모분산을 아는데 모분산이 동일할 경우)

EX-03) 모평균이 뮤_1 = 5 , 뮤_2 = 3 , 모분산_1 = 모분산_2 = 9이고 서로 독립인 두 정규모집단에서 각각 크기가 64인 표본을 추출, 첫 번째 모집단의 표본평균을 |X , 두 번째 모집단의 표본평균을 |Y 라 할때 | |X - |Y | 가 3보다 클 확률
U = |X- |Y
n = m = 64
U의 표본평균 = 5 -3 = 2
U의 표본분산 = 9/64 + 9/64 = 18/64
U ~ N(2 , 18/64)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((3-2) / math.sqrt(18/64) ,2)
print(z_1)
# z_2 = round((2-0) / math.sqrt(25/64) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) | (x<=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = stats.norm.cdf(-z_1)
ax.text(2.61 , .05, f'P({z_1}>=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.3, .017), xytext=(2.5 , .05) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(-3.71 , .055, f'P(Z<={-z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(-2.3, .017), xytext=(-2.5 , .05) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
plt.annotate('' , xy=(0, .2), xytext=(-2.5 , .08) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(0, .2), xytext=(2.5 , .08) , arrowprops = dict(facecolor = 'black'))
ax.text(-1 , .21, f'P({-z_1}<=Z<={z_1}) : {round(area*2,4)}',fontsize=15)
P(|U| > 3) = P(|Z| > (3 - 2) / 루트(18/64) ) = 2 * P(Z< 1/루트(18/64) = 0.0588
EX-04) 모평균과 모분산이 각각 뮤_1 = 5 , 뮤_2 = 4 , 분산_1 = 분산_2 = 9 , 서로 독립인 두 정규모집단에서 각각 크기 n=m=100인 표본을 추출하였다. 첫 번째 모집단의 표본평균을 |X , 두번째 모집단의 표본평균을 |Y라 할때,
| |X - |Y | 가 2보다 작을 확률을 구하라.
U = |X - |Y
U의 표본평균 = 5 -4 = 1
U의 표본분산 = 9/100 + 9/100 = 18/100
U ~ N(1 , 18/100)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((2-1) / math.sqrt(18/100) ,2)
# z_2 = round((2-1) / math.sqrt(18/100) ,2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area_1 = ( stats.norm.cdf(z_1) - stats.norm.cdf(- z_1) )
ax.text(2.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area_1,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(2.5 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
P(|U| < 2) = P(|Z| < 2-1 /루트(18/100) ) = P( Z<2-1 /루트(18/100)) - P( Z< -(2-1 /루트(18/100))) = P(-2.36 <= Z <= 2.36) = 0.9817
4. 두 표본평균의 차에 대한 중심극한정리에 의한 표본분포
https://knowallworld.tistory.com/303
★lineplot★중심극한정리★기초통계학-[모집단 분포와 표본분포 -04]
1. 중심극한정리 ==> 정규분포가 아닌 모집단 분포로부터 복원추출로 표본 선정시 ==> 표본의 크기에 따라 표본평균의 표본분포가 변한다. ==> 모평균 뮤 , 모분산(o**2) 의 임의의 모집단으로부터
knowallworld.tistory.com
https://knowallworld.tistory.com/304
★중심극한정리★기초통계학-[모집단 분포와 표본분포 -05]
EX-01) 남성의 평균 결혼연령 32세 , 분산 8.41세 , 36명 임의로 선정하여 표본조사 1> 평균 결혼 연령의 근사 표본분포 n = 36 >= 30 이므로 중심극한 정리에 의하여 평균결혼 연령은 |X ~ N(32 , 8.41/ 36) 2>
knowallworld.tistory.com


EX-05) 남자 평균키 173.38cm , 표준편차 5.75cm , 여자 평균 160.39cm , 표준편차 4.99cm , 남성과 여성 각각 150명 선정했을 때, 남성의 평균 키가 여성의 평균 키보다 14cm 이상 클 확률
뮤_|x = 173.38 , s_|x = 5.75
뮤_|y = 160.39 , s_|y = 4.99
n = m = 150 >= 30 ==> 중심극한정리 사용 가능
P(|X - |Y >= 14)
U = |X - |Y
u_m = 173.38 - 160.39
u_v = 5.75**2 / 150 + 4.99**2 / 150
print(f'U의 표본평균 {u_m}')
print(f'U의 표본분산 {u_v}')U의 표본평균 : 173.38 - 160.39 = 12.99
U의 표본분산 : 0.3864
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((14 - 12.99 ) / math.sqrt(0.3864) ,2)
#z_2 = round((200-185) / math.sqrt(900/36) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- (stats.norm.cdf(z_1))
ax.text(2.15 , .045, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.5, .017), xytext=(2.7 , .04) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
P(U>=14) = P(Z>= 14 -12.99 / 루트(0.3864) ) = 1 - P(Z<=14 -12.99 / 루트(0.3864)) = 1- P(Z<=1.62) = 0.0526
EX-06) 남성의 몸무게는 평균 66.55kg , 표준편차가 8.46kg, 여성의 몸무게는 55.74kg , 표준편차 5.42kg이라 하자. 남성 150명 , 여성 150명 선정 ==> 평균 몸무게가 여성의 평균 몸무게보다 12kg 이상 클 확률
뮤_|X = 66.55
s_|x = 8.46
뮤_|Y = 55.74
s_|y = 5.42
n=m = 150
P(|X-|Y >= 12)
U = |X - |Y
U의 평균 : 66.55 -55.74 = 10.809
U의 표본분산 : 0.673
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((12 - 10.809 ) / math.sqrt(0.673) ,2)
#z_2 = round((200-185) / math.sqrt(900/36) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- (stats.norm.cdf(z_1))
ax.text(2.15 , .045, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.5, .017), xytext=(2.7 , .04) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
P(U>=12) = P(Z >= (12-10.809 / 루트(0.673) ) ) = 1 - P(Z<= (12-10.809 / 루트(0.673) ) ) = 1 - P(Z<=1.45) = 0.0735
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★서로독립인 정규집단의 표본분산(모분산은 알때) 추론★카이제곱분포★합동표본분산에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -10] (0) | 2023.01.07 |
|---|---|
| ★두 표본평균의 차에 대한 표본분포(모분산 모를때)★중심극한정리 활용★이표본의 표본분포★기초통계학-[모집단 분포와 표본분포 -09] (0) | 2023.01.06 |
| 이항분포에 따른 정규분포의 표준정규분포화★표본비율의 표본분포★기초통계학-[모집단 분포와 표본분포 -07] (0) | 2023.01.06 |
| ★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집단 분포와 표본분포 -06] (0) | 2023.01.06 |
| ★중심극한정리★기초통계학-[모집단 분포와 표본분포 -05] (0) | 2023.01.06 |
이항분포에 따른 정규분포의 표준정규분포화★표본비율의 표본분포★기초통계학-[모집단 분포와 표본분포 -07]
1.표본비율의 표본분포
EX) 이항 확률변수의 실질적인 응용 ==> 여론조사 생각
==> 모집단을 구성하는 사람들의 어느 특정 사건을 선호하는 비율(p)를 알기 위하여 n명으로 구성된 표본을 임의 선정
==> n명 중 x명이 특정사건 선호
==> n명으로 구성된 표본 중에서 특정 사건을 선호하는 비율(성공률)인 표본 비율 ^p = x/n
==>개개인이 특정 사건에 대해 선호하는 비율이 독립적으로 p이므로
==> 표본으로 선정된 n명 중에서 특정 사건을 선호하는 사람의 수를 X라 하면 X~B(n, p) 이다.
https://knowallworld.tistory.com/241
이항분포식★이항실험★이항분포의 평균,분산★베르누이시행★기초통계학-[Chapter05 - 이산확률
1. 이항분포 ==> 많이 사용하는 확률 모형 : 이항분포, 푸아송분포 , 초기하분포 1. 이항실험(Bionomial Experiment) ==> 실험은 N번의 시행 ==> 실험 결과는 성공(S) , 실패(F) ==> 성공 확률 : p , 실패 확률 : q
knowallworld.tistory.com
==> X의 평균과 분산은 각각 np , npq이다.
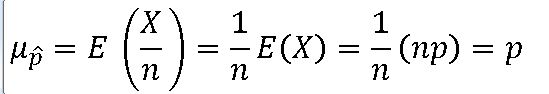
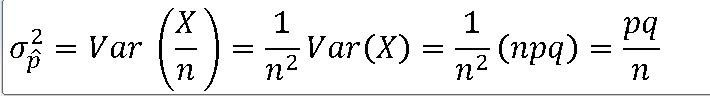
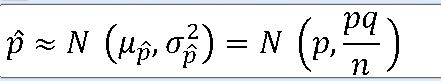
=> 표본비율 ^p의 확률분포는 평균(뮤) 과 분산(o**2)을 갖는 정규분포에 근사한다.
EX-01) 응답률 21.1%로 박지성 존경. 응답률이 전체 대학생의 생각이라는 가정아래 500명의 대학생을 임의로 선정했을 때 박지성에 대한 지지율이 25%를 넘을 확률
n = 500
p = 0.211
q = 1- 0.211 = 0.789
n = 500
p = 0.211
q = 1- 0.211
print(f'평균 : {n*p}')
print(f'분산 : {n*p*q}')표본비율의 평균 = 105.5 / 500 = 0.211
표본비율의 분산 = 83.2395 / 500**2 = 0.00033
==> 박지성에 대한 지지율을 ^p라하자.
^p ~ N(0.211 , 0.000333 )
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.25-0.211) / math.sqrt(0.000333) ,2)
#z_2 = round((200-185) / math.sqrt(900/36) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- (stats.norm.cdf(z_1))
ax.text(2.15 , .045, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.5, .017), xytext=(2.7 , .04) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))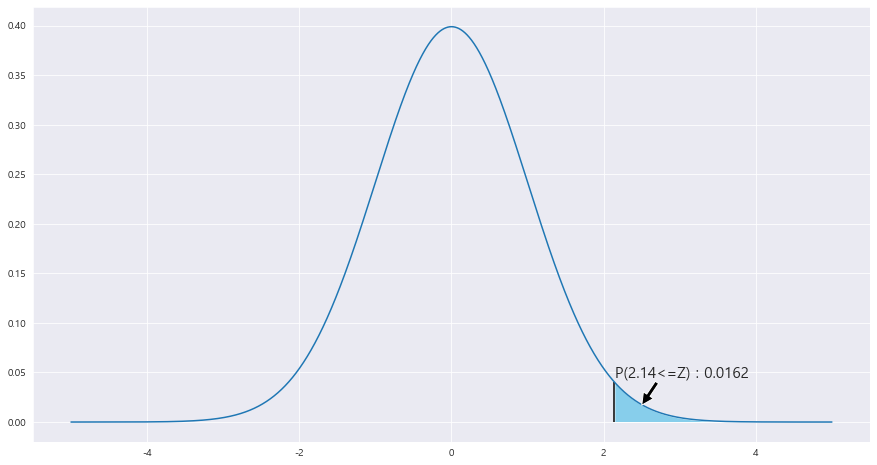
P(^p > 0.25) = P( (^p - 0.211 / 루트(0.00033) )> 0.25-0.211 / 루트(0.000332) ) = P(Z>= 2.14) = 0.0158
EX-02) 35명의 왼손잡이가 포함된 1000명의 어린이 중 무작위로 40명 선정
1> 선정된 어린이 중에서 적어도 2명의 왼손잡이가 있을 확률
https://knowallworld.tistory.com/254
정규분포의 표준정규분포로의 변환★기초통계학-[Chapter06 - 연속확률분포-03]
1. 정규분포와 표준정규분포의 관계 =========================== ==> P(z_a =2.5 , facecolor = 'skyblue') # x값 , y값 , 0 , x= 2.5) = P(Z 박테리아의 수가 75마리 이상 103마리 이하일 확률 P(75
knowallworld.tistory.com
==> 이항분포에 따른 정규분포의 표준정규분포로의 변환
n = 40
p = 35/1000 = 0.035
q = 1 - 0.035 = 0.865
40명안에 포함된 왼손잡이 어린이 수를 X라 하면 , X ~ B(40 , 0.035) 이다. X ~N(1.4 , 1.351)
E(X) = np = 1.4
V(X) = npq = 1.351
P(X > 2 ) = P(Z > 2-1.4 / 루트(1.351) ) = 0.3015
==>답지가 틀린듯?
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((2 - 1.4 ) / math.sqrt(1.351) ,2)
#z_2 = round((200-185) / math.sqrt(900/36) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- (stats.norm.cdf(z_1))
ax.text(2.15 , .045, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.5, .017), xytext=(2.7 , .04) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))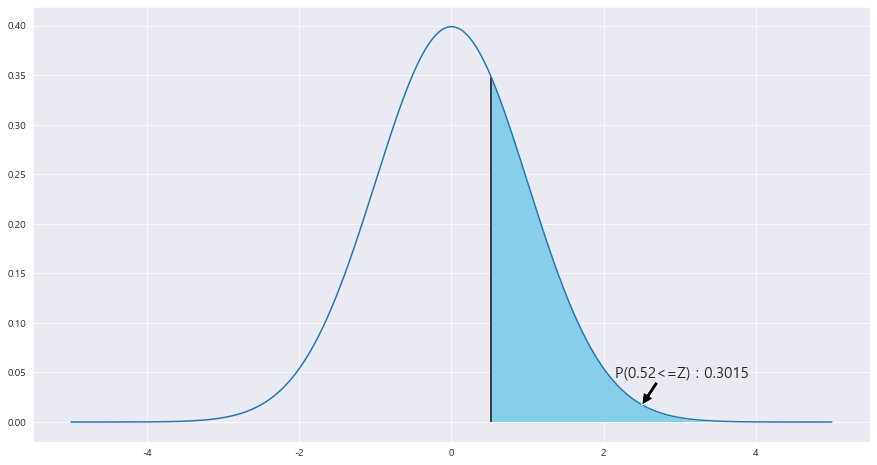
2> 선정된 어린이 중에서 왼손잡이의 비율이 5% 이상일 확률
n = 40
p = 0.035
q = 1- 0.035
print(f'평균 : {n*p / n}')
print(f'분산 : {n*p*q / n**2}')표본비율의 평균 = 40 * 0.035 / 40 = 0.035
표본비율의 분산 = 40 * 0.035 * 0.865 / 40**2 = 0.00084
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((0.05 - 0.035 ) / math.sqrt(0.00084) ,2)
#z_2 = round((200-185) / math.sqrt(900/36) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- (stats.norm.cdf(z_1))
ax.text(2.15 , .045, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.5, .017), xytext=(2.7 , .04) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
P(^p > 0.05 ) = P(Z > 0.05 - 0.035 / 루트(0.00084) ) = 1 - P( (0.05 -0.035) / 루트(0.00084)) = P(0.52<=Z) = 0.3015
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★두 표본평균의 차에 대한 표본분포(모분산 모를때)★중심극한정리 활용★이표본의 표본분포★기초통계학-[모집단 분포와 표본분포 -09] (0) | 2023.01.06 |
|---|---|
| ★두 표본평균의 차에 대한 표본분포(모분산 알때 , 동일할때)★중심극한정리 활용★이표본의 표본분포★기초통계학-[모집단 분포와 표본분포 -08] (0) | 2023.01.06 |
| ★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집단 분포와 표본분포 -06] (0) | 2023.01.06 |
| ★중심극한정리★기초통계학-[모집단 분포와 표본분포 -05] (0) | 2023.01.06 |
| ★lineplot★중심극한정리★기초통계학-[모집단 분포와 표본분포 -04] (0) | 2023.01.05 |
★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집단 분포와 표본분포 -06]
1. 모분산의 표본분포
정규모집단 N(뮤 , 모분산) 으로부터 크기 n인 표본을 선정할 때 표본분산

==> 표본분산 S**2에 대한 표본분포는 X**2-통계량 V에 대하여 자유도가 n-1인 카이제곱분포이다.
https://knowallworld.tistory.com/258
★scipy.stats.chi2().ppf()★matplotlib 수학식표현★카이제곱분포★정규분포★기초통계학-[Chapter06 - 연
1. 카이제곱분포 ==> 카이제곱분포는 정규모집단의 모분산에 대한 통계적 추론에 사용 ==> n개의 서로 독립인 표준정규확률변수 Z_1 ,Z_2 ,···· Z_n 에 대하여 확률변수의 확률분포를 자유도(degree of
knowallworld.tistory.com
==> 카이제곱분포


==> 정규모집단 N(뮤 , 모분산)에서 모분산을 추정하거나 검정하기 위하여 표본분산 S**2을 이용한다.
==> 확률분포는 카이제곱분포를 활용한다!!!
EX-01) 감기약의 무게는 분산이 0.000756g인 정규분포를 따른다. 감기약 16개를 수거하여 무게 측정
1> 표본분산과 관련된 x**2 - 통계량 V의 분포를 구하라.
모분산 = 0.000756g , 확률분포(n) = 16
==> 표본분산과 관련한 표본분포는 자유도 15인 카이제곱분포이다.
V = (16-1)* (S**2) / 0.000756 ~ X**2(15)
2> 표본조사 결과 [4.23 , 4.26 , 4.26 , 4.24 , 4.27 , 4.23 , 4.19 , 4.27 , 4.21 , 4.25 , 4.23 , 4.29 , 4.30 , 4.24 , 4.20 , 4.24]
관찰된 표본분산의 값 s**2를 구하라.
표본평균 = 4.244
표본분산(s_0**2) = 0.00092
3> 이 표본을 이용하여 통계량의 관찰값 X**2_0 = (n-1)* s_0**2 / 모분산 을 구하라.
n-1 = 16 -1 = 15
s_0**2 = 0.00092
모분산 = 0.000756
sik = (15*(0.00092)) / 0.000756X**2_0 = 18.25
4> 표본분산 S**2 이 관찰값 s_0**2보다 클 확률
P(S**2 > s_0**2) = P(S**2 > 0.00092 ) = P(15*S**2 / 0.000756 > 15*s_0**2 / 0.000756 ) = P(V > 15*(0.0009**2) / 0.000756) = P(V>= 18.25) = 0.249
matplotlib.rc("font" , family = "Times New Roman" , weight = "bold")
X = np.arange(0,30,.01)
fig = plt.figure(figsize=(15,8))
dof = 15 #자유도
ax = sns.lineplot(X , scipy.stats.chi2(dof).pdf(X))
X_r = 18.25
print(X_r)
chai = scipy.stats.chi2(dof).pdf(18.25)
print(chai)
ax.fill_between(X, scipy.stats.chi2(dof).pdf(X) , where = (X>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = 1- scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(25 , .015, 'P(X >' + r'$\chi^2_{0.05})$' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(22, .002), xytext=(24 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 3.5, .018, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
plt.annotate('' , xy=(17.5, .002), xytext=(15 , .014) , arrowprops = dict(facecolor = 'black'))
b = [r'$\chi^2(\eta$ = {})'.format(15)]
print(b)
plt.legend(b , fontsize = 15)
EX-02) 제주도 펜션 사용료 분산 8.03, [12.5 , 11.5 , 6.0, 5.5 , 15.5 , 11.5 , 10.5 , 17.5 , 10.0 , 9.5 , 13.5 , 8.5 , 11.5 , 15.5 , 10.5]
1> x**2 ~ 통계량 V의 분포를 구하고, 관찰된 표본분산의 값 s_0**2 을 구하라.
모분산 = 8.03
표본평균 = 11.3
표본분산 = 11.1357
n = 15
V = (15-1)* (S**2) / 8.03 ~ X**2(14)
2> 통계량의 관찰값 X_0**2 = (n-1)*s_0**2 / 분산 을 구하라
print(14 * 11.1357 / 8.03)
X_0**2 = 14* 11.1357 / 8.03 = 19.414
3> 표본분산 S**2 이 s_0**2보다 클확률
P(S**2 > s_0**2) = P(14 * S**2 / 8.03 > 14* 11.1357 / 8.03) = P (V > 19.414) = 0.1497
matplotlib.rc("font" , family = "Times New Roman" , weight = "bold")
X = np.arange(0,30,.01)
fig = plt.figure(figsize=(15,8))
dof = 14 #자유도
ax = sns.lineplot(X , scipy.stats.chi2(dof).pdf(X))
X_r = 19.414
print(X_r)
chai = scipy.stats.chi2(dof).pdf(18.25)
print(chai)
ax.fill_between(X, scipy.stats.chi2(dof).pdf(X) , where = (X>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = 1- scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(25 , .015, 'P(X >' + r'$\chi^2_{0.04})$' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(22, .002), xytext=(24 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 3.5, .018, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
plt.annotate('' , xy=(19.41, .002), xytext=(18 , .014) , arrowprops = dict(facecolor = 'black'))
b = [r'$\chi^2(\eta$ = {})'.format(14)]
print(b)
plt.legend(b , fontsize = 15)

출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★두 표본평균의 차에 대한 표본분포(모분산 알때 , 동일할때)★중심극한정리 활용★이표본의 표본분포★기초통계학-[모집단 분포와 표본분포 -08] (0) | 2023.01.06 |
|---|---|
| 이항분포에 따른 정규분포의 표준정규분포화★표본비율의 표본분포★기초통계학-[모집단 분포와 표본분포 -07] (0) | 2023.01.06 |
| ★중심극한정리★기초통계학-[모집단 분포와 표본분포 -05] (0) | 2023.01.06 |
| ★lineplot★중심극한정리★기초통계학-[모집단 분포와 표본분포 -04] (0) | 2023.01.05 |
| ★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본★표본비율★기초통계학-[모집단 분포와 표본분포 -03] (0) | 2023.01.05 |