1. 이표본의 표본분포
==>지금까지는 단일 모집단의 표본에 대한 통계량의 표본분포
EX) 수능에서 남학생, 여학생 집단의 평균이 동일한지 여부 비교
==> 비교위해서는 각각 표본을 추출하여야 한다.
==> 서로 독립인 두 모집단의 모수를 비교하기 위해서는 각각 표본을 추출하고, 두 표본으로부터 적당한 통계량을 산출해야한다.
2. 두 표본평균의 차에 대한 표본분포(두 모분산을 아는 경우)
==> 두 모분산을 알고 있고, 서로 독립인 정규모집단 N(뮤_1 , o_1**2) , N(뮤_2 , o_2**2) 로부터 각각 n과 m인 표본을 추출했을 때, 각각의 표본평균을 |X, |Y라 하자.
https://knowallworld.tistory.com/302
★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본
1. 표본평균의 표본분포(모분산을 아는 경우) ==> 표본평균에 대한 표본분포는 정규분포를 따른다. EX-01) 모평균 100 , 모분산 9인 정규모집단으로부터 크기 25인 표본을 임의로 추출 1> 표본평균 |X
knowallworld.tistory.com
==> 표본평균 : N(뮤_1 , o_1**2 / n) , N (뮤_2 , o_2**2 / m)
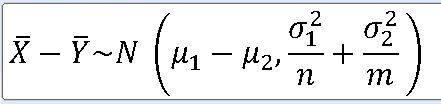
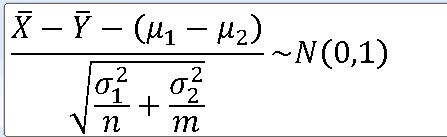
EX-01) 모분산이 각각 9 , 16이고 동일한 모 평균을 갖는 서로 독립인 두 정규모집단에서 각각 크기가 n=m = 64인 표본을 추출하였다. 첫 번째 모집단의 표본평균을 |X , 두번째 모집단의 표본평균을 |Y라 할때 | |X - |Y | 가 2보다 클 확률
==> 표본평균 N( |X , 9) , N( |Y , 16)
==> |X - |Y의 분산 = 9/ 64 + 16/64 = 25 /64
==> U = |X - |Y라하면 U ~ N(0, 25/64)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((-2-0) / math.sqrt(25/64) ,2)
z_2 = round((2-0) / math.sqrt(25/64) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_2) & (x<= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area_1 = 1 - stats.norm.cdf(z_2)
area_2 = stats.norm.cdf(z_1)
ax.text(2.71 , .034, f'P({z_2}<=Z) : {round(area_1,4)}',fontsize=15)
plt.annotate('' , xy=(3.3, .0017), xytext=(3.5 , .03) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(-3.71 , .034, f'P(Z<={z_1}) : {round(area_2,4)}',fontsize=15)
plt.annotate('' , xy=(-3.3, .0017), xytext=(-3.5 , .03) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))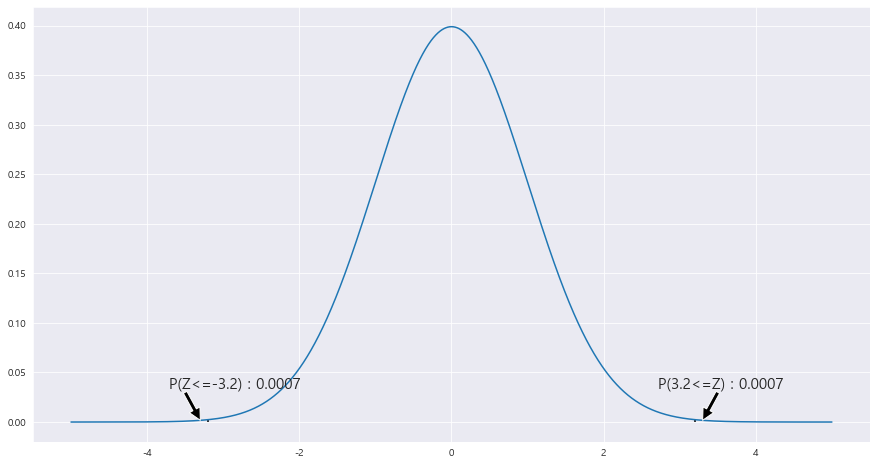
P(| |X- |Y | >=2 ) = P( U>=2) + P(U<=-2) = P( Z>= (2 -0) / 루트(25/64) ) + P( Z<= -2 -0 / 루트(25/64) ) = 1 - P( Z<= (2 -0) / 루트(25/64) ) + P( Z<= -2 -0 / 루트(25/64) ) = 0.0007 + 0.0007 = 0.0014
EX-02) 모평균과 모분산이 각각 뮤_1 = 5 , 뮤_2 = 4 , 분산_1 = 9 , 분산_2 = 16 , 서로 독립인 두 정규모집단에서 각각 크기 n=m=100인 표본을 추출하였다. 첫 번째 모집단의 표본평균을 |X , 두번째 모집단의 표본평균을 |Y라 할때,
| |X - |Y | 가 2보다 작을 확률을 구하라.
U = |X - |Y
U의 평균 = 5- 4 = 1
U의 분산 = 9/100 + 16/100 = 25 /100
U ~ N(1 , 25/100)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((2-1) / math.sqrt(25/100) ,2)
# z_2 = round((2-0) / math.sqrt(25/64) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=-z_1) & (x<= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area_1 = ( stats.norm.cdf(z_1) - stats.norm.cdf(0) ) * 2
ax.text(2.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area_1,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(2.5 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))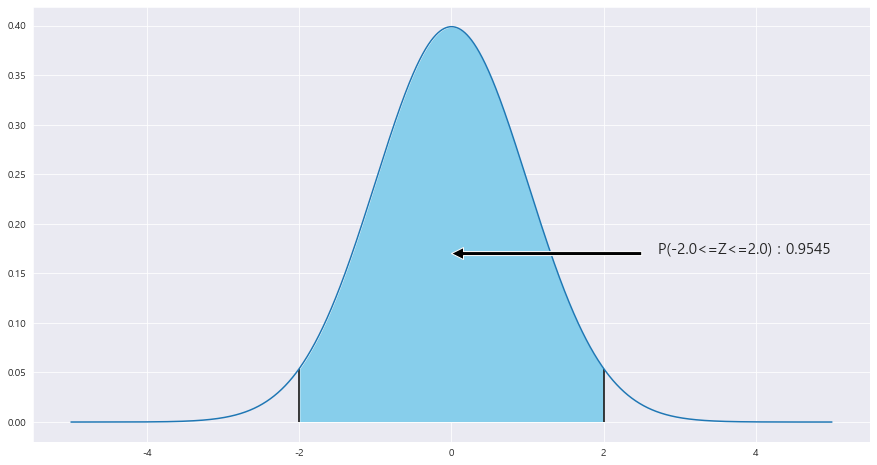
P(|U| <2) = P(-2< U < 2) = (P(U<2) - P(U<0) ) * 2 = (P(Z< (2-1) / 루트(25/100)) - 0.5) * 2 = P(-2 <= Z <= 2) = 0.9545
3. 두 표본평균의 차에 대한 표본분포(두 모분산을 아는데 모분산이 동일할 경우)
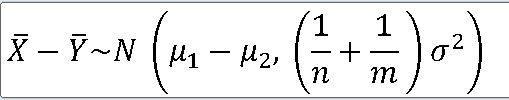
EX-03) 모평균이 뮤_1 = 5 , 뮤_2 = 3 , 모분산_1 = 모분산_2 = 9이고 서로 독립인 두 정규모집단에서 각각 크기가 64인 표본을 추출, 첫 번째 모집단의 표본평균을 |X , 두 번째 모집단의 표본평균을 |Y 라 할때 | |X - |Y | 가 3보다 클 확률
U = |X- |Y
n = m = 64
U의 표본평균 = 5 -3 = 2
U의 표본분산 = 9/64 + 9/64 = 18/64
U ~ N(2 , 18/64)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((3-2) / math.sqrt(18/64) ,2)
print(z_1)
# z_2 = round((2-0) / math.sqrt(25/64) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) | (x<=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = stats.norm.cdf(-z_1)
ax.text(2.61 , .05, f'P({z_1}>=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.3, .017), xytext=(2.5 , .05) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(-3.71 , .055, f'P(Z<={-z_1}) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(-2.3, .017), xytext=(-2.5 , .05) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
plt.annotate('' , xy=(0, .2), xytext=(-2.5 , .08) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(0, .2), xytext=(2.5 , .08) , arrowprops = dict(facecolor = 'black'))
ax.text(-1 , .21, f'P({-z_1}<=Z<={z_1}) : {round(area*2,4)}',fontsize=15)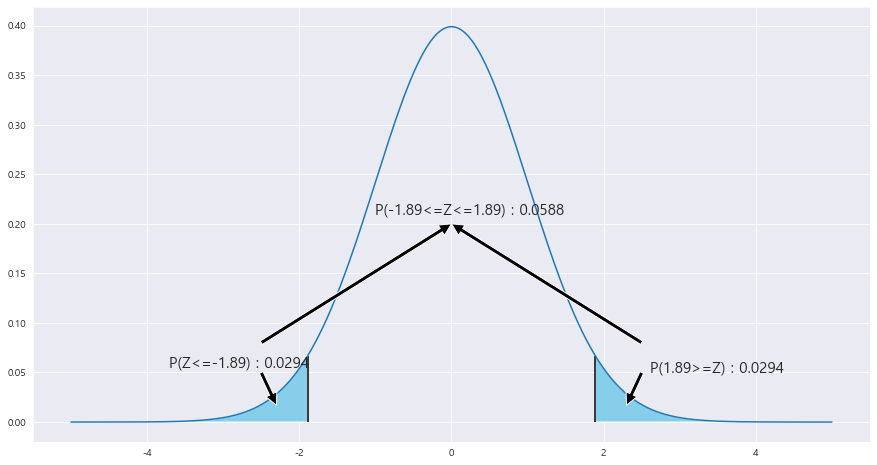
P(|U| > 3) = P(|Z| > (3 - 2) / 루트(18/64) ) = 2 * P(Z< 1/루트(18/64) = 0.0588
EX-04) 모평균과 모분산이 각각 뮤_1 = 5 , 뮤_2 = 4 , 분산_1 = 분산_2 = 9 , 서로 독립인 두 정규모집단에서 각각 크기 n=m=100인 표본을 추출하였다. 첫 번째 모집단의 표본평균을 |X , 두번째 모집단의 표본평균을 |Y라 할때,
| |X - |Y | 가 2보다 작을 확률을 구하라.
U = |X - |Y
U의 표본평균 = 5 -4 = 1
U의 표본분산 = 9/100 + 9/100 = 18/100
U ~ N(1 , 18/100)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((2-1) / math.sqrt(18/100) ,2)
# z_2 = round((2-1) / math.sqrt(18/100) ,2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area_1 = ( stats.norm.cdf(z_1) - stats.norm.cdf(- z_1) )
ax.text(2.71 , .17, f'P({-z_1}<=Z<={z_1}) : {round(area_1,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(2.5 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))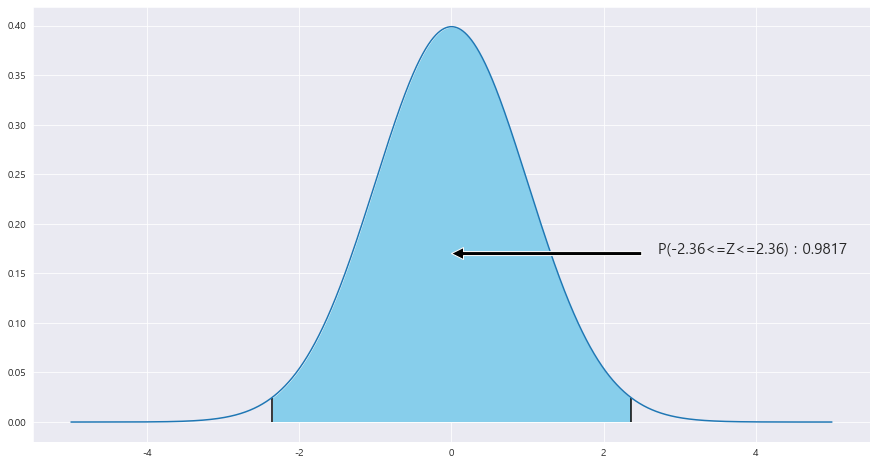
P(|U| < 2) = P(|Z| < 2-1 /루트(18/100) ) = P( Z<2-1 /루트(18/100)) - P( Z< -(2-1 /루트(18/100))) = P(-2.36 <= Z <= 2.36) = 0.9817
4. 두 표본평균의 차에 대한 중심극한정리에 의한 표본분포
https://knowallworld.tistory.com/303
★lineplot★중심극한정리★기초통계학-[모집단 분포와 표본분포 -04]
1. 중심극한정리 ==> 정규분포가 아닌 모집단 분포로부터 복원추출로 표본 선정시 ==> 표본의 크기에 따라 표본평균의 표본분포가 변한다. ==> 모평균 뮤 , 모분산(o**2) 의 임의의 모집단으로부터
knowallworld.tistory.com
https://knowallworld.tistory.com/304
★중심극한정리★기초통계학-[모집단 분포와 표본분포 -05]
EX-01) 남성의 평균 결혼연령 32세 , 분산 8.41세 , 36명 임의로 선정하여 표본조사 1> 평균 결혼 연령의 근사 표본분포 n = 36 >= 30 이므로 중심극한 정리에 의하여 평균결혼 연령은 |X ~ N(32 , 8.41/ 36) 2>
knowallworld.tistory.com
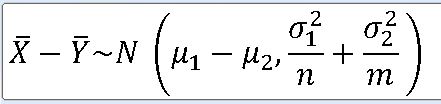
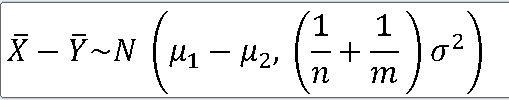
EX-05) 남자 평균키 173.38cm , 표준편차 5.75cm , 여자 평균 160.39cm , 표준편차 4.99cm , 남성과 여성 각각 150명 선정했을 때, 남성의 평균 키가 여성의 평균 키보다 14cm 이상 클 확률
뮤_|x = 173.38 , s_|x = 5.75
뮤_|y = 160.39 , s_|y = 4.99
n = m = 150 >= 30 ==> 중심극한정리 사용 가능
P(|X - |Y >= 14)
U = |X - |Y
u_m = 173.38 - 160.39
u_v = 5.75**2 / 150 + 4.99**2 / 150
print(f'U의 표본평균 {u_m}')
print(f'U의 표본분산 {u_v}')U의 표본평균 : 173.38 - 160.39 = 12.99
U의 표본분산 : 0.3864
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((14 - 12.99 ) / math.sqrt(0.3864) ,2)
#z_2 = round((200-185) / math.sqrt(900/36) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- (stats.norm.cdf(z_1))
ax.text(2.15 , .045, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.5, .017), xytext=(2.7 , .04) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))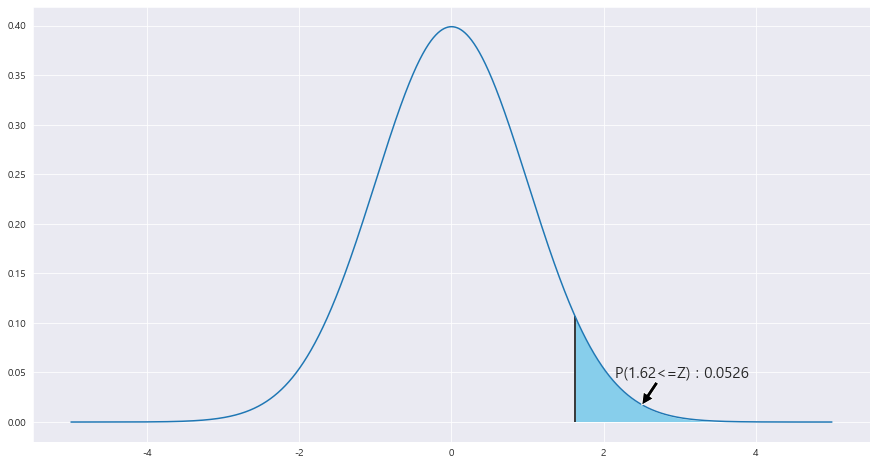
P(U>=14) = P(Z>= 14 -12.99 / 루트(0.3864) ) = 1 - P(Z<=14 -12.99 / 루트(0.3864)) = 1- P(Z<=1.62) = 0.0526
EX-06) 남성의 몸무게는 평균 66.55kg , 표준편차가 8.46kg, 여성의 몸무게는 55.74kg , 표준편차 5.42kg이라 하자. 남성 150명 , 여성 150명 선정 ==> 평균 몸무게가 여성의 평균 몸무게보다 12kg 이상 클 확률
뮤_|X = 66.55
s_|x = 8.46
뮤_|Y = 55.74
s_|y = 5.42
n=m = 150
P(|X-|Y >= 12)
U = |X - |Y
U의 평균 : 66.55 -55.74 = 10.809
U의 표본분산 : 0.673
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
z_1 = round((12 - 10.809 ) / math.sqrt(0.673) ,2)
#z_2 = round((200-185) / math.sqrt(900/36) , 2)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>= z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- (stats.norm.cdf(z_1))
ax.text(2.15 , .045, f'P({z_1}<=Z) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.5, .017), xytext=(2.7 , .04) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
# ax.vlines(x= z_2, ymin= 0 , ymax= stats.norm.pdf(z_2, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))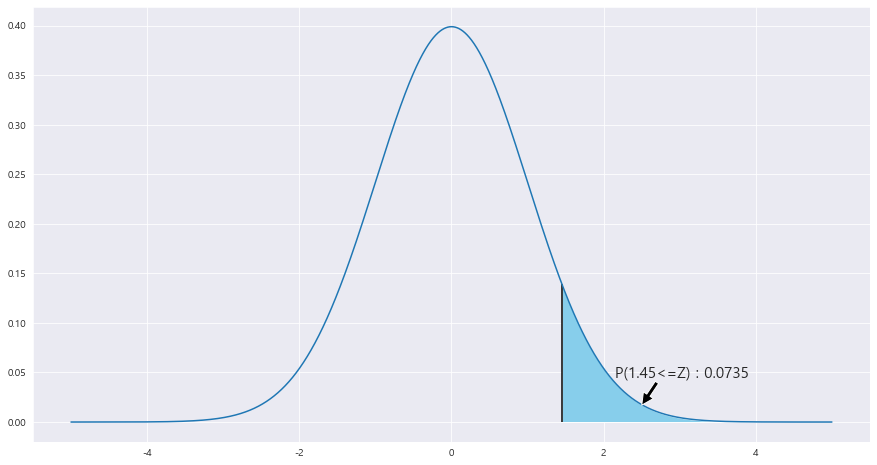
P(U>=12) = P(Z >= (12-10.809 / 루트(0.673) ) ) = 1 - P(Z<= (12-10.809 / 루트(0.673) ) ) = 1 - P(Z<=1.45) = 0.0735
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★서로독립인 정규집단의 표본분산(모분산은 알때) 추론★카이제곱분포★합동표본분산에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -10] (0) | 2023.01.07 |
|---|---|
| ★두 표본평균의 차에 대한 표본분포(모분산 모를때)★중심극한정리 활용★이표본의 표본분포★기초통계학-[모집단 분포와 표본분포 -09] (0) | 2023.01.06 |
| 이항분포에 따른 정규분포의 표준정규분포화★표본비율의 표본분포★기초통계학-[모집단 분포와 표본분포 -07] (0) | 2023.01.06 |
| ★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집단 분포와 표본분포 -06] (0) | 2023.01.06 |
| ★중심극한정리★기초통계학-[모집단 분포와 표본분포 -05] (0) | 2023.01.06 |