★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집단 분포와 표본분포 -06]
1. 모분산의 표본분포
정규모집단 N(뮤 , 모분산) 으로부터 크기 n인 표본을 선정할 때 표본분산
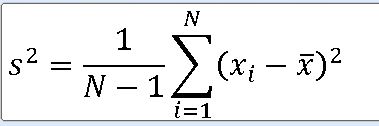
==> 표본분산 S**2에 대한 표본분포는 X**2-통계량 V에 대하여 자유도가 n-1인 카이제곱분포이다.
https://knowallworld.tistory.com/258
★scipy.stats.chi2().ppf()★matplotlib 수학식표현★카이제곱분포★정규분포★기초통계학-[Chapter06 - 연
1. 카이제곱분포 ==> 카이제곱분포는 정규모집단의 모분산에 대한 통계적 추론에 사용 ==> n개의 서로 독립인 표준정규확률변수 Z_1 ,Z_2 ,···· Z_n 에 대하여 확률변수의 확률분포를 자유도(degree of
knowallworld.tistory.com
==> 카이제곱분포

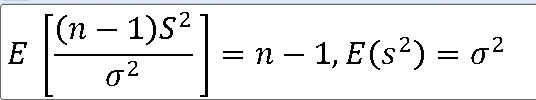
==> 정규모집단 N(뮤 , 모분산)에서 모분산을 추정하거나 검정하기 위하여 표본분산 S**2을 이용한다.
==> 확률분포는 카이제곱분포를 활용한다!!!
EX-01) 감기약의 무게는 분산이 0.000756g인 정규분포를 따른다. 감기약 16개를 수거하여 무게 측정
1> 표본분산과 관련된 x**2 - 통계량 V의 분포를 구하라.
모분산 = 0.000756g , 확률분포(n) = 16
==> 표본분산과 관련한 표본분포는 자유도 15인 카이제곱분포이다.
V = (16-1)* (S**2) / 0.000756 ~ X**2(15)
2> 표본조사 결과 [4.23 , 4.26 , 4.26 , 4.24 , 4.27 , 4.23 , 4.19 , 4.27 , 4.21 , 4.25 , 4.23 , 4.29 , 4.30 , 4.24 , 4.20 , 4.24]
관찰된 표본분산의 값 s**2를 구하라.
표본평균 = 4.244
표본분산(s_0**2) = 0.00092
3> 이 표본을 이용하여 통계량의 관찰값 X**2_0 = (n-1)* s_0**2 / 모분산 을 구하라.
n-1 = 16 -1 = 15
s_0**2 = 0.00092
모분산 = 0.000756
sik = (15*(0.00092)) / 0.000756X**2_0 = 18.25
4> 표본분산 S**2 이 관찰값 s_0**2보다 클 확률
P(S**2 > s_0**2) = P(S**2 > 0.00092 ) = P(15*S**2 / 0.000756 > 15*s_0**2 / 0.000756 ) = P(V > 15*(0.0009**2) / 0.000756) = P(V>= 18.25) = 0.249
matplotlib.rc("font" , family = "Times New Roman" , weight = "bold")
X = np.arange(0,30,.01)
fig = plt.figure(figsize=(15,8))
dof = 15 #자유도
ax = sns.lineplot(X , scipy.stats.chi2(dof).pdf(X))
X_r = 18.25
print(X_r)
chai = scipy.stats.chi2(dof).pdf(18.25)
print(chai)
ax.fill_between(X, scipy.stats.chi2(dof).pdf(X) , where = (X>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = 1- scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(25 , .015, 'P(X >' + r'$\chi^2_{0.05})$' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(22, .002), xytext=(24 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 3.5, .018, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
plt.annotate('' , xy=(17.5, .002), xytext=(15 , .014) , arrowprops = dict(facecolor = 'black'))
b = [r'$\chi^2(\eta$ = {})'.format(15)]
print(b)
plt.legend(b , fontsize = 15)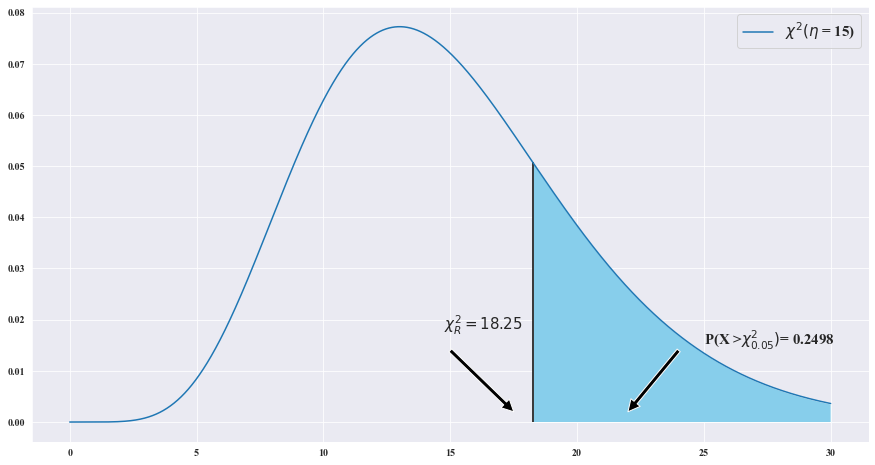
EX-02) 제주도 펜션 사용료 분산 8.03, [12.5 , 11.5 , 6.0, 5.5 , 15.5 , 11.5 , 10.5 , 17.5 , 10.0 , 9.5 , 13.5 , 8.5 , 11.5 , 15.5 , 10.5]
1> x**2 ~ 통계량 V의 분포를 구하고, 관찰된 표본분산의 값 s_0**2 을 구하라.
모분산 = 8.03
표본평균 = 11.3
표본분산 = 11.1357
n = 15
V = (15-1)* (S**2) / 8.03 ~ X**2(14)
2> 통계량의 관찰값 X_0**2 = (n-1)*s_0**2 / 분산 을 구하라
print(14 * 11.1357 / 8.03)
X_0**2 = 14* 11.1357 / 8.03 = 19.414
3> 표본분산 S**2 이 s_0**2보다 클확률
P(S**2 > s_0**2) = P(14 * S**2 / 8.03 > 14* 11.1357 / 8.03) = P (V > 19.414) = 0.1497
matplotlib.rc("font" , family = "Times New Roman" , weight = "bold")
X = np.arange(0,30,.01)
fig = plt.figure(figsize=(15,8))
dof = 14 #자유도
ax = sns.lineplot(X , scipy.stats.chi2(dof).pdf(X))
X_r = 19.414
print(X_r)
chai = scipy.stats.chi2(dof).pdf(18.25)
print(chai)
ax.fill_between(X, scipy.stats.chi2(dof).pdf(X) , where = (X>=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = 1- scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(25 , .015, 'P(X >' + r'$\chi^2_{0.04})$' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(22, .002), xytext=(24 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 3.5, .018, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
plt.annotate('' , xy=(19.41, .002), xytext=(18 , .014) , arrowprops = dict(facecolor = 'black'))
b = [r'$\chi^2(\eta$ = {})'.format(14)]
print(b)
plt.legend(b , fontsize = 15)

출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★두 표본평균의 차에 대한 표본분포(모분산 알때 , 동일할때)★중심극한정리 활용★이표본의 표본분포★기초통계학-[모집단 분포와 표본분포 -08] (0) | 2023.01.06 |
|---|---|
| 이항분포에 따른 정규분포의 표준정규분포화★표본비율의 표본분포★기초통계학-[모집단 분포와 표본분포 -07] (0) | 2023.01.06 |
| ★중심극한정리★기초통계학-[모집단 분포와 표본분포 -05] (0) | 2023.01.06 |
| ★lineplot★중심극한정리★기초통계학-[모집단 분포와 표본분포 -04] (0) | 2023.01.05 |
| ★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본★표본비율★기초통계학-[모집단 분포와 표본분포 -03] (0) | 2023.01.05 |