★확률질량함수의 평균 분산★그룹화자료의 평균과 분산이 아닌 확률질량함수이다!!!★이산균등분포★기초통계학-[연습문제01 -13]
1. 모집단분포가 이산균등분포 X ~ DU(6)인 모집단으로부터 크기 2인 표본을 임의 추출
==> 이산균등분포
1> 표본으로 나올 수 있는 모든 경우의 수
==> 복원추출에 의한 2개씩 뽑는다.
A = list(itertools.product(np.arange(1,7) , repeat = 2))
A[(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1),
(3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)]
2> 각 표본의 평균
각 표본의 평균 : [1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, 3.5, 4.0, 4.5, 5.0, 5.5, 6.0]
표본들의 평균 :[1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, 5.5, 6.0]
3> 표본평균 |X의 확률분포
a = list(itertools.product(np.arange(1,7) , repeat = 2))
# print(a)
b = list(map(lambda x : np.mean(x) , a))
d = deque()
for i in zip(a,b):
d.append(i)
c = sorted(list(set(list(map(lambda x : np.mean(x) , a)))))
d = deque(sorted(d , key = lambda x : x[1]))
e =[[] for i in range(len(c))]
# print(type(d))
# print(len(a))
p=0
while len(d)>=2:
if d[0][1] == d[1][1]:
e[p].append(d[0][0])
# print(f'e: {e}')
d.popleft()
# print(f'd: {d}')
else:
e[p].append(d[0][0])
# print(f'일치 x e: {e}')
d.popleft()
p+=1
e[p].append(d[-1][0])
B = pd.DataFrame([e ,c]).T
B.rename(columns= {0 : '표본' , 1: '|X'} , inplace = True)
B
b_len = [len(i) for i in B['표본']]
b_len
B['표본길이'] = b_len
B['P(|X = x)'] = B['표본길이'] / len(a)
B['평균'] = B['|X'] * B['P(|X = x)']
B['분산'] = (B['|X']**2) * B['P(|X = x)']
a = pd.DataFrame(B[:].sum(axis=0))
# a.transpose()
a = a.transpose()
col_name = a.columns.tolist()
for i in range(len(col_name[:-3])):
a.iloc[0][i] = '-'
a.iloc[0][3] = '결과값'
a.iloc[0][5] = a.iloc[0][5] - a.iloc[0][4]**2
B = pd.concat([B ,a])
B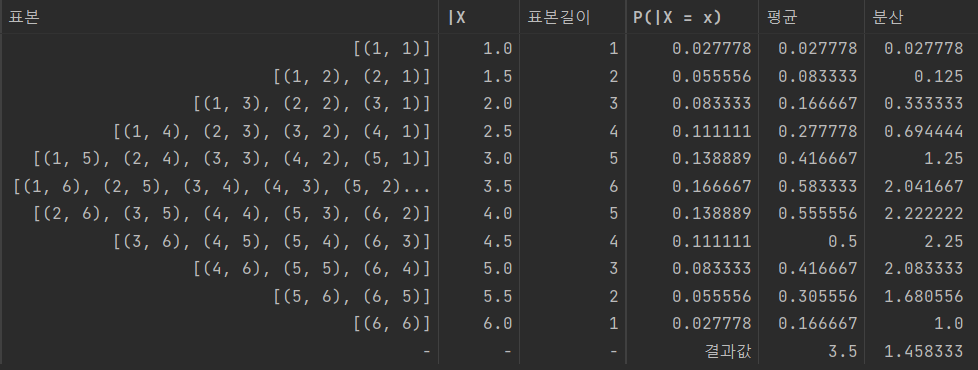
B.iloc[:-1, [1,3]]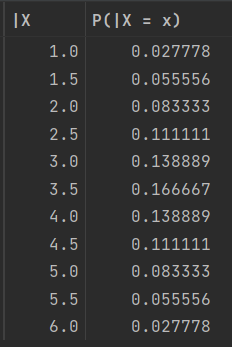
4> 표본평균 |X의 평균과 분산
평균 : 3.5
분산 : 1.45833
np.var(각 표본들의 평균 , ddof=0) ==> 모분산
5> 모집단분포의 평균과 분산을 구하라.
x = 1, 2, 3, 4, 5, 6
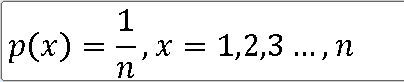
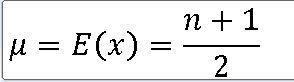
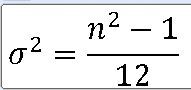
https://knowallworld.tistory.com/245
★초기하분포★기하분포★이산균등분포★기초통계학-[Chapter05 - 이산확률분포-06]
1. 이산균등분포(Discrete Uniform Distribution) 1> 동전을 한 번 던져서 앞면이 나온 횟수를 X ==> p(x) = 1/2 , x= 0 ,1 2> 주사위를 한 번 던질 때 나온 눈의 수를 확률 변수 X라 하면 ==> p(x) = 1/6 , x =1 , 2, 3, 4, 5,
knowallworld.tistory.com
평균 : (1 + 6) / 2 = 3.5
분산 : (6**2 -1) / 12 = 2.9217
2. 모집단의 확률분포가 p(1) = 0.8 , p(2) = 0.2 인 양의 비대칭일 때, 이 모집단으로부터 크기 2인 표본을 임의로 추출한다.
https://knowallworld.tistory.com/241
이항분포식★이항실험★이항분포의 평균,분산★베르누이시행★기초통계학-[Chapter05 - 이산확률
1. 이항분포 ==> 많이 사용하는 확률 모형 : 이항분포, 푸아송분포 , 초기하분포 1. 이항실험(Bionomial Experiment) ==> 실험은 N번의 시행 ==> 실험 결과는 성공(S) , 실패(F) ==> 성공 확률 : p , 실패 확률 : q
knowallworld.tistory.com
==> 성공확률 0.8인 이항분포식 ==> but. 이항분포식은 횟수가 지정되어야 한다.
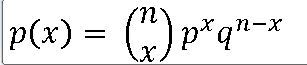
https://knowallworld.tistory.com/218
insert() , index★그룹화 자료의 분산과 표준편차★기초통계학-[Chapter03 - 07]
1. 그룹화 자료의 분산과 표준편차 A ='29 30 49 21 39 38 15 39 48 41 50 38 33 40 51 29 31 42 29 69 37 20 49 40 10 49 49 49 35 45 22 45 20 45 30 41 40 38 10 31 47 19 31 21 41 46 28 29 18 28' A = list(map(int, A.split(' '))) A A = [29, 30, 49, 21,
knowallworld.tistory.com
==> 그룹화 자료의 분산
https://knowallworld.tistory.com/240
표본,모표본★평균과 분산★기초통계학-[Chapter05 - 이산확률분포-02]
1. 평균 ==> 이산확률변수의 확률 히스토그램 ==> 상대도수히스토그램과 유사 But. 상대도수히스토그램은 n개의 자료 값에 대한 표본 설명 확률 히스토그램은 실험에서 발생할 수 있는 모든 경우에
knowallworld.tistory.com
==> 이 문제는 확률질량함수 이다!!!!!!!!!!!!!!!!!!!!!!!!!
1> 표본으로 나올 수 있는 모든 경우의 수
x = 1, 2
모든 경우의 수 : [(1, 1), (1, 2), (2, 1), (2, 2)]
2> 각표본의 평균
각 표본별 평균 : [1.0, 1.5, 1.5, 2.0]
표본들의 평균 : [1.0 , 1.5 , 2.0]
==> 계급값이라고 생각하자!!!
3> 표본평균 |X의 확률분포를 구하라.
# print(a)
b = list(map(lambda x : np.mean(x) , a))
d = deque()
for i in zip(a,b):
d.append(i)
c = sorted(list(set(list(map(lambda x : np.mean(x) , a)))))
d = deque(sorted(d , key = lambda x : x[1]))
e =[[] for i in range(len(c))]
# print(type(d))
# print(len(a))
p=0
while len(d)>=2:
if d[0][1] == d[1][1]:
e[p].append(d[0][0])
# print(f'e: {e}')
d.popleft()
# print(f'd: {d}')
else:
e[p].append(d[0][0])
# print(f'일치 x e: {e}')
d.popleft()
p+=1
e[p].append(d[-1][0])
B = pd.DataFrame([e ,c]).T
B.rename(columns= {0 : '표본' , 1: '|X'} , inplace = True)
b_len = [len(i) for i in B['표본']]
b_len
B['표본길이'] = b_len
B
P_X = [(0.8** i[0].count(1) * 0.2**i[0].count(2) * len(i)) for i in B['표본']]
B['P(|X = x)'] = P_X
B['평균'] = B['|X'] * B['P(|X = x)']
B['분산'] = (B['|X']**2) * B['P(|X = x)']
a = pd.DataFrame(B[:].sum(axis=0))
# a.transpose()
a = a.transpose()
col_name = a.columns.tolist()
for i in range(len(col_name[:-3])):
a.iloc[0][i] = '-'
a.iloc[0][3] = '결과값'
a.iloc[0][5] = a.iloc[0][5] - a.iloc[0][4]**2 #분산 = |X**2 * P(X) - 평균**2
B = pd.concat([B ,a])
B
P_X = [(0.8** i[0].count(1) * 0.2**i[0].count(2) * len(i)) for i in B['표본']]==> 확률 P(|X = x)
B.iloc[:-1 , [1,3]]
|X = 1 , 0.8*0.8 = 0.64
|X = 2 , 0.8*0.2 *2 = 0.16 *2 = 0.32
|X = 3 , 0.2 *0.2 = 0.04
4> 표본평균 |X의 평균과 분산을 구하라.
평균 : 1.2
분산 : 0.08( |X**2 - P(X) - 평균의 제곱)
5>모집단분포의 평균과 분산을 구하라.

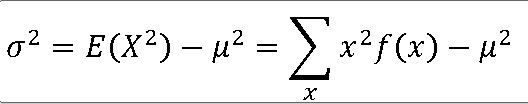
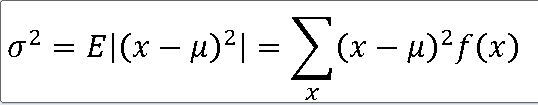
평균 : 1*0.8 + 2*0.2 = 0.8 + 0.4 = 1.2
분산 : [(1-1.2)**2]*0.8 + [(2-1.2)**2]*0.2 = 0.16
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★Solve()이후 float로의 변환★크기를 알때/모를때의 표본평균의 표준분포★기초통계학-[연습문제02 -15] (0) | 2023.01.09 |
|---|---|
| ★표본평균의 정규분포(표본평균 = 모평균 , 표본분산 = 모분산/크기)★모분산 모를때 정규표본 추출★기초통계학-[연습문제02 -14] (0) | 2023.01.09 |
| ★표본비율의 차에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -12] (0) | 2023.01.07 |
| ★F-분포★두 표본분산의 비에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -11] (1) | 2023.01.07 |
| ★서로독립인 정규집단의 표본분산(모분산은 알때) 추론★카이제곱분포★합동표본분산에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -10] (0) | 2023.01.07 |