★lineplot★중심극한정리★기초통계학-[모집단 분포와 표본분포 -04]
1. 중심극한정리
==> 정규분포가 아닌 모집단 분포로부터 복원추출로 표본 선정시
==> 표본의 크기에 따라 표본평균의 표본분포가 변한다.
==> 모평균 뮤 , 모분산(o**2) 의 임의의 모집단으로부터 크기 n인 표본을 선정할 때 , n이 충분히 크면(n>=30) 표본평균 |X의 확률분포는 평균 뮤 , 분산 (o**2 / 루트(n))의 정규분포에 근사
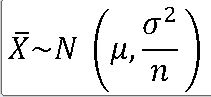

==> 모집단의 크기가 충분하다
==> 모집단으로부터 비복원추출로 확률표본을 선정했을 때의 표본평균 |X의 표본분포 역시 복원추출로 표본을 선정했을 때의 표본분포와 동일
x = 1 , 2, 3, 4 인 모집단 분포 ==> 모집단 분포가 이산균등분포이므로
모평균 = 4+1 / 2 = 2.5
모분산 = (16 - 1) /12 = 1.25
1) x = 1,2,3,4 n=2
a = list(itertools.product(np.arange(1,4) , repeat = 2))
print(a)
b = list(map(lambda x : np.mean(x) , a))
d = deque()
for i in zip(a,b):
d.append(i)
c = sorted(list(set(list(map(lambda x : np.mean(x) , a)))))
print(b)
print(c)
print(d)
a = [(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)]
b = [1.0, 1.5, 2.0, 2.5, 1.5, 2.0, 2.5, 3.0, 2.0, 2.5, 3.0, 3.5, 2.5, 3.0, 3.5, 4.0]
c = [1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0]
d= deque([((1, 1), 1.0), ((1, 2), 1.5), ((1, 3), 2.0), ((1, 4), 2.5), ((2, 1), 1.5), ((2, 2), 2.0), ((2, 3), 2.5), ((2, 4), 3.0), ((3, 1), 2.0), ((3, 2), 2.5), ((3, 3), 3.0), ((3, 4), 3.5), ((4, 1), 2.5), ((4, 2), 3.0), ((4, 3), 3.5), ((4, 4), 4.0)])
d = deque(sorted(d , key = lambda x : x[1]))
e =[[] for i in range(len(c))]
p=0
print(len(d))==> 16
while len(d)>=2:
if d[0][1] == d[1][1]:
e[p].append(d[0][0])
print(f'e: {e}')
d.popleft()
print(f'd: {d}')
else:
e[p].append(d[0][0])
print(f'일치 x e: {e}')
d.popleft()
p+=1
e[p].append(d[-1][0])
e[[(1, 1)], [(1, 2), (2, 1)], [(1, 3), (2, 2), (3, 1)], [(1, 4), (2, 3), (3, 2), (4, 1)], [(2, 4), (3, 3), (4, 2)], [(3, 4), (4, 3)], [(4, 4)]]
B = pd.DataFrame([e ,c]).T
B.rename(columns= {0 : '표본' , 1: '|X'} , inplace = True)
B
b_len = [len(i) for i in B['표본']]
b_len
B['표본길이'] = b_len
B['P(|X = x)'] = B['표본길이'] / len(a)
B['평균'] = B['|X'] * B['P(|X = x)']
B['분산'] = (B['|X']**2) * B['P(|X = x)']
B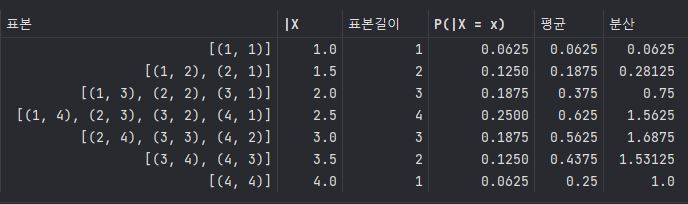
a = pd.DataFrame(B[:].sum(axis=0))
a = a.transpose()
col_name = a.columns.tolist()
for i in range(len(col_name[:-3])):
a.iloc[0][i] = '-'
a.iloc[0][3] = '결과값'
a.iloc[0][5] = a.iloc[0][5] - a.iloc[0][4]**2
B = pd.concat([B ,a])
B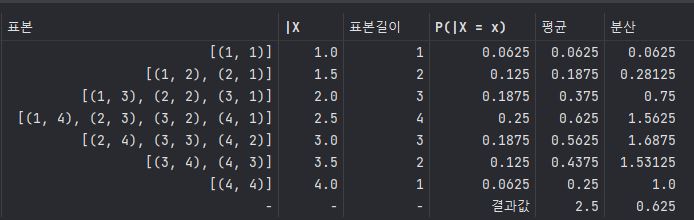
==> 평균 : 2.5 , 분산 : 0.625
x= C.columns.tolist()
print(x)
# x = np.arange(7)
# print(x)
y = C.iloc[0, :].tolist()
print(y)
fig = plt.figure(figsize=(10,8)) #plt는 matplotlib의 약자
fig.set_facecolor('white')
ax = sns.lineplot(x=x, y=y,
color='r', # 색상
linestyle='-', # 라인 스타일
marker='o') # 마커
#ax 변수에 저장
ax.set_title('n = 2 인 경우' , fontsize = 15)
ax.set_xlabel('X', fontsize = 15 , fontweight = 'bold')
ax.set_ylabel(r'P($\bar X = \bar x$)' , fontsize = 15 , fontweight = 'bold' , rotation = 0 , labelpad=25)
# ax.set_xticklabels(x, fontsize=15) #set_xticklabels(축별 이름 , font 크기)
ax.vlines(x= x, ymin= 0 , ymax= [y] , color = 'black' , linestyle ='dashed' , label ='{}'.format(2) , )==> ax.set_xtickslabels() --> 하면 x축 값이 이상한 이유는 뭘까?

2) x = 1,2,3,4 n=3
a = list(itertools.product(np.arange(1,5) , repeat = 3))
# print(a)
b = list(map(lambda x : np.mean(x) , a))
d = deque()
for i in zip(a,b):
d.append(i)
c = sorted(list(set(list(map(lambda x : np.mean(x) , a)))))
d = deque(sorted(d , key = lambda x : x[1]))
e =[[] for i in range(len(c))]
# print(type(d))
# print(len(a))
p=0
while len(d)>=2:
if d[0][1] == d[1][1]:
e[p].append(d[0][0])
# print(f'e: {e}')
d.popleft()
# print(f'd: {d}')
else:
e[p].append(d[0][0])
# print(f'일치 x e: {e}')
d.popleft()
p+=1
e[p].append(d[-1][0])
B = pd.DataFrame([e ,c]).T
B.rename(columns= {0 : '표본' , 1: '|X'} , inplace = True)
B
b_len = [len(i) for i in B['표본']]
b_len
B['표본길이'] = b_len
B['P(|X = x)'] = B['표본길이'] / len(a)
B['평균'] = B['|X'] * B['P(|X = x)']
B['분산'] = (B['|X']**2) * B['P(|X = x)']
a = pd.DataFrame(B[:].sum(axis=0))
# a.transpose()
a = a.transpose()
col_name = a.columns.tolist()
for i in range(len(col_name[:-3])):
a.iloc[0][i] = '-'
a.iloc[0][3] = '결과값'
a.iloc[0][5] = a.iloc[0][5] - a.iloc[0][4]**2
B = pd.concat([B ,a])
B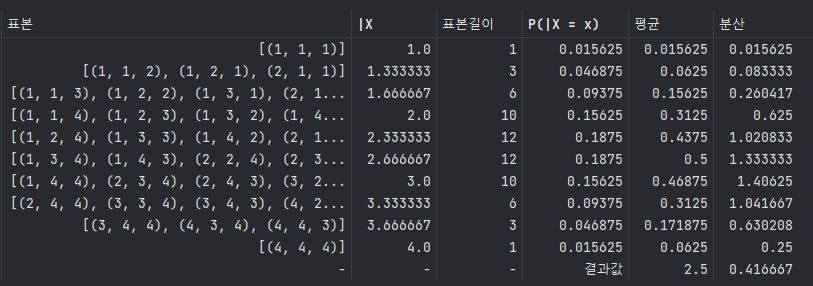
C = B.iloc[ :-1 , [1, 3]]
C = C.set_index('|X')
C = C.T
C
x= C.columns.tolist()
print(x)
# x = np.arange(7)
# print(x)
y = C.iloc[0, :].tolist()
print(y)
fig = plt.figure(figsize=(10,8)) #plt는 matplotlib의 약자
fig.set_facecolor('white')
ax = sns.lineplot(x=x, y=y,
color='r', # 색상
linestyle='-', # 라인 스타일
marker='o') # 마커
#ax 변수에 저장
ax.set_title('n = 3 인 경우' , fontsize = 15)
ax.set_xlabel('X', fontsize = 15 , fontweight = 'bold')
ax.set_ylabel(r'P($\bar X = \bar x$)' , fontsize = 15 , fontweight = 'bold' , rotation = 0 , labelpad=25)
# ax.set_xticklabels(x, fontsize=15) #set_xticklabels(축별 이름 , font 크기)
ax.vlines(x= x, ymin= 0 , ymax= [y] , color = 'black' , linestyle ='dashed' , label ='{}'.format(2) , )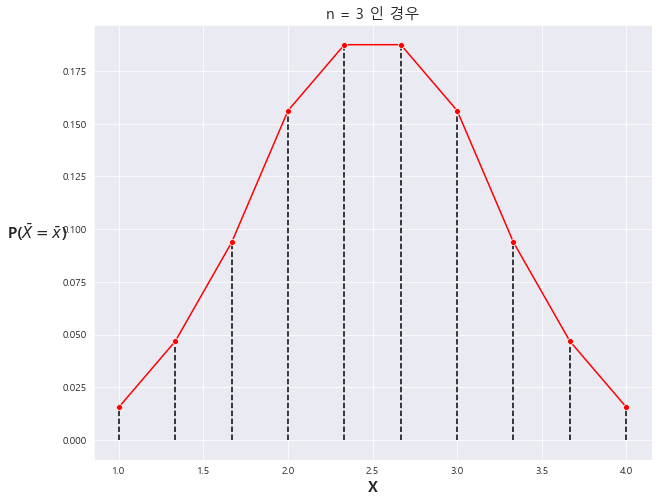
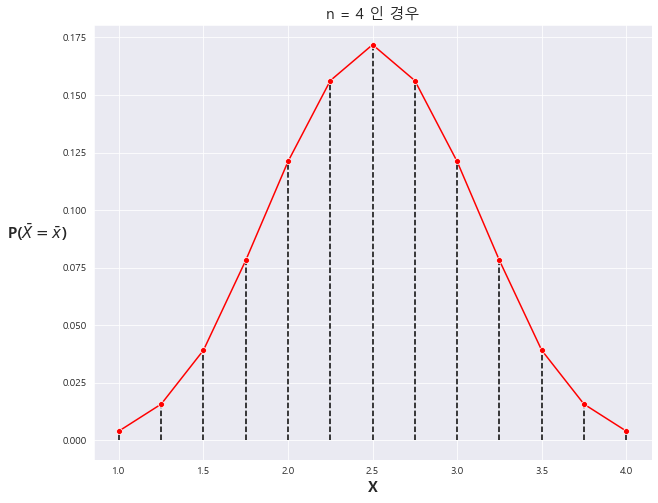
3) x = 1,2,3,4 n=4
4) x = 1,2,3,4 n=5
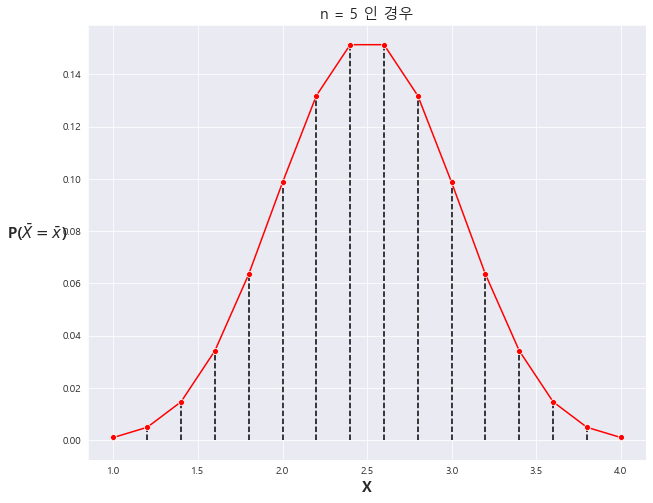
==> n이 충분히 크면 평균 뮤 , 분산 : (모분산/n) 정규분포에 근사하게 된다!!!!
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집단 분포와 표본분포 -06] (0) | 2023.01.06 |
|---|---|
| ★중심극한정리★기초통계학-[모집단 분포와 표본분포 -05] (0) | 2023.01.06 |
| ★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본★표본비율★기초통계학-[모집단 분포와 표본분포 -03] (0) | 2023.01.05 |
| ★모비율★표본비율★기초통계학-[모집단 분포와 표본분포 -02] (0) | 2023.01.05 |
| ★표본분포★이산균등분포★표본추출 방법★모집단 분포★기초통계학-[모집단 분포와 표본분포 -01] (1) | 2023.01.05 |