전체 글
-
푸아송분포★기초통계학-[Chapter05 - 이산확률분포-04]2022.12.14
-
표본,모표본★평균과 분산★기초통계학-[Chapter05 - 이산확률분포-02]2022.12.14
-
★lambda , filter★기초통계학-[Chapter04 - 연습문제-02]2022.12.12
[외교부 인턴 일지- d+100 2022.12.14]데이터 분석 청년인재 양성 사업
D+100 이다!!
더욱더 열심히 해보자!!!
기초통계쪽 개념 잡는데 생각보다 오래걸린다.(1월 초까지는 마무리 해야한다.)
딥러닝도 빨리 파자!
필기 준비도 계속하자!
코테도 해야한다!
할거 많다!!
'인턴일지 > 외교부_일지' 카테고리의 다른 글
| [외교부 인턴 일지- d+115 2022.12.26]데이터 분석 청년인재 양성 사업 (0) | 2022.12.29 |
|---|---|
| [외교부 인턴 일지- d+109 2022.12.23]데이터 분석 청년인재 양성 사업 (1) | 2022.12.23 |
| [외교부 인턴 일지- d+86 2022.11.30]데이터 분석 청년인재 양성 사업 (0) | 2022.12.01 |
| [외교부 인턴 일지- d+85 2022.11.29]데이터 분석 청년인재 양성 사업 (0) | 2022.11.29 |
| [외교부 인턴 일지- d+84]데이터 분석 청년인재 양성 사업 (0) | 2022.11.28 |
푸아송분포★기초통계학-[Chapter05 - 이산확률분포-04]
1.푸아송 분포
==> 이항분포에 대한 확률을 계산하기 위하여 누적이항확률표 사용
==> but. 시행(n)이 30보다 큰 경우의 확률표 X
==> 시행(n)이 30보다 클 경우의 확률 근사값 구할 수 있다.
1> 확률 실험은 주어진 구간에서 사건이 발생한 횟수 X, 상태공간 {0 , 1 ,2 ,3 ,4 , ······· }
2> 동일한 크기의 구간에서 사건이 발생할 확률은 동일
3> 겹치지 않는 구간에서 사건이 발생한 횟수는 서로 독립

==> 뮤는 평균
==> 분산도 뮤
EX-01) 월평균 3회인 푸아송분포에 따라 교통사고가 일어난다.
1> 한 달 동안 4건의 사고가 발생할 확률
X ~ p(3) ==> 뮤(평균) 는 3
P(X = 4) = P(X<=4) - P(X<=3) = 0.815 - 0.647 ==> 누적푸아송확률분포표 참고
2> 두달동안 4건의 사고가 발생할 확률
두달의 평균 ==> 6회
Y ~ p(6)
P(Y=4) = P(Y<=4) - P(Y<=3) = 0.285-0.151 = 0.134 ==> 누적푸아송확률분포표 참고
EX-02) 시간당 평균 4명의 손님 , 9시 ~ 9시 30분 꼭 1명의 손님이 찾아올 확률 , 10시 ~ 12시까지 손님이 5명이상 찾아올 확률
X ~ p(4)
====
뮤 = 2
P( X = 1) = P(X>=1) - P(X <= 0) = 0.406-0.135 = 0.271
====
뮤 = 8
P(X>=5) = 1- P(X<=4) = 1-0.1 = 0.9

출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 이산확률변수' 카테고리의 다른 글
| ★초기하분포★기하분포★이산균등분포★기초통계학-[Chapter05 - 이산확률분포-06] (0) | 2022.12.15 |
|---|---|
| ★Seaborn에서의 Subplots★이항확률의 근사 확률★푸아송분포★기초통계학-[Chapter05 - 이산확률분포-05] (0) | 2022.12.15 |
| 이항분포식★이항실험★이항분포의 평균,분산★베르누이시행★기초통계학-[Chapter05 - 이산확률분포-03] (1) | 2022.12.14 |
| 표본,모표본★평균과 분산★기초통계학-[Chapter05 - 이산확률분포-02] (0) | 2022.12.14 |
| ★key, value , items() , sorted(key =), loc로 행추가!★확률분포★기초통계학-[Chapter05 - 이산확률분포-01] (0) | 2022.12.14 |
이항분포식★이항실험★이항분포의 평균,분산★베르누이시행★기초통계학-[Chapter05 - 이산확률분포-03]
1. 이항분포
==> 많이 사용하는 확률 모형 : 이항분포, 푸아송분포 , 초기하분포
1. 이항실험(Bionomial Experiment)
==> 실험은 N번의 시행
==> 실험 결과는 성공(S) , 실패(F)
==> 성공 확률 : p , 실패 확률 : q = 1- p ==> 확률 변수 X는 p의 베르누이 분포 이룬다.
==> 매 시행은 독립적, 이전 결과가 다음 시행에 영향 X
==> N번 중 성공 횟수 x에 관심
==> 베르누이 실험을 독립적으로 n번 시행 ==> 이항실험
EX) 주사위 3번 ==> 1이 나온 횟수에 관심
P(X =1 ) , P(X = 0 ) ==> 확률변수 X 는 1이 성공 0 이 실패
P(X = 1) = 1/6 , P(X = 0 ) = 5/6
2. 이항분포(Bionomial Distribution)
==> 매회 성공률이 p인 베르누이 시행을 독립적으로 n번 반복하여 시행
X ~ B(n , p)
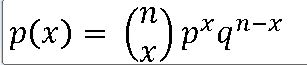
EX-01 ) 5지 선다 10문제에서 임의로 답안 선택
1> 정답을 선택한 문제 수에 대한 확률함수
P(X = 1) = 0.2 P(X = 0) = 0.8
len(list(itertools.combinations(np.arange(10) , x)))*(math.pow(0.2 , x)) *(math.pow(0.8 , n-x)) #n은 전체 갯수 , x는 맞춘 갯수==> x는 맞춘횟수 , n은 전체 횟수
2> 꼭 2문제를 맞힐 확률
X ~ B(10 , 0.2)
b = len(list(itertools.combinations(np.arange(10) , 2)))*(math.pow(0.2 , 2)) *(math.pow(0.8 , 8))
print(b)p(x) = 10C2 * (0.2 ** 2) * (0.8 ** 8) = 0.302
3> 1문제 이상 맞힐 확률
==> 1 - 모든 문제를 틀릴 확률
x = 0
b = 1- len(list(itertools.combinations(np.arange(10) , 0)))*(math.pow(0.2 , 0)) *(math.pow(0.8 , 10)) #n은 전체 갯수 , x는 맞춘 갯수
print(b)p(x) = 1- 10C0 * (0.2 **0) * (0.8 ** 10) = 0.8926
EX-02 ) 매회 성공률이 0.3인 베르누이 시행을 독립적으로 4번 반복
1> 성공한 횟수에 대한 확률함수
P(X = 1) = 0.3 P(X = 0) = 0.7
f(x) = nCx * (0.3 ** x) * (0.7 ** (n-x))
= 4Cx * (0.3 ** x) * (0.7 ** (4-x)) , x=0,1,2,3
2> 2번 성공할 확률
f(x = 2 ) = 4C2 * (0.3 **2) * (0.7 ** 2) = 0.2646
EX-03) 출국자수 1485만 , 30% 출국 ==> 10명 무작위 선정
1> 출국 경험이 있는 사람이 4명 이하일 확률
P(X <= 4) = 0.8497
2>정확히 3명
P(X = 3) = P(X<=3) - P(X<=2) = 0.6496-0.3828 = 0.2668
3> 5명 이상일 확률
P(X>=5) = 1- P(X<= 4) = 1 - 0.8497 = 0.1503
p(X = 1) = p = 0.3
p(X = 0) = q= 0.7
EX-04) A는 6번 시도 , 상품을 판매할 확률 30% , B는 9번 시도 판매확률 30%
1> A,B 함께 판매한 상품이 5개일 확률
A : X~ B(6 , 0.3)
B : X~ B(9, 0.3)
S : X ~ B(6+9 , 0.3) = X ~ B(15 , 0.3)
P(S = 5) = P(S<=5) - P(S<= 4) = 0.7216 -0.5155 = 0.2061 ==> 누적이항확률표 참고
2> A가 판매한 상품수가 x(x = 0 , 1 , 2 ,3 ,4 ,5)개이고 B가 판매한 상품 수 가 5- x개일 확률
이항분포:
A : X~ B(6 , 0.3) ==> P(X) = 6Cx * (0.3 ** x) * (0.7 ** 6-x)
B : X~ B(9, 0.3) ==> P(X) = 9Cx * (0.3 ** 5-x) * (0.7 ** 9-(5-x))
P(A = 0 ) = 0.1176
P(B = 5-0) = 0.0735
for x in range(6):
a = len(list(itertools.combinations(np.arange(6) , x)))*(math.pow(0.3 , x)) *(math.pow(0.7 , 6-x))
b = len(list(itertools.combinations(np.arange(9) , 5-x)))*(math.pow(0.3 , 5-x)) *(math.pow(0.7 , 9-(5-x)))
# print('a : {}'.format(a))
# print('b : {}'.format(b))
s = a*b
print('P(x = {} , y = {}) , s : {}'.format(x , 5-x , s))P(x = 0 , y = 5) , s : 0.008648827173881995
P(x = 1 , y = 4) , s : 0.05189296304329196
P(x = 2 , y = 3) , s : 0.08648827173881993
P(x = 3 , y = 2) , s : 0.04942186956503996
P(x = 4 , y = 1) , s : 0.009266600543444992
P(x = 5 , y = 0) , s : 0.0004118489130419996
3> A,B 함께 판매한 상품이 모두 5개일때 A가 판매한 상품이 3개일 확률
sume = 0
for x in range(6):
a = len(list(itertools.combinations(np.arange(6) , x)))*(math.pow(0.3 , x)) *(math.pow(0.7 , 6-x))
b = len(list(itertools.combinations(np.arange(9) , 5-x)))*(math.pow(0.3 , 5-x)) *(math.pow(0.7 , 9-(5-x)))
# print('a : {}'.format(a))
# print('b : {}'.format(b))
s = a*b
sume += s
print('P(x = {} , y = {}) , s : {}'.format(x , 5-x , s))
print(sume)P(x = 3 , y = 2) , s : 0.04942186956503996
P(X+Y = 5 ) = 0.2061
P(X = 3 | X + Y = 5) = 0.0494 / 0.2061
EX-05) A,B 공장 불량률 5% , A,B 각각 5대씩 판매할 때 불량품이 꼭 하나 있을 확률 , 적어도 하나 있을 확률
불량품이 꼭 하나 있을 확률 : P(X+Y = 1)
불량품이 적어도 하나 있을 확률 : P(X+Y >= 1) = 1- + P( X+Y = 0))
A : X ~ B (5 , 0.05)
B : X ~ B (5 , 0.05)
p(A) = 5Cx * (0.05 ** x) * (0.95 ** 5-x)
p(B) = 5Cx * (0.05 ** x) * (0.95 ** 5-x)
sume = 0
for x in range(2):
a = len(list(itertools.combinations(np.arange(5) , x)))*(math.pow(0.3 , x)) *(math.pow(0.7 , 5-x))
b = len(list(itertools.combinations(np.arange(5) , 1-x)))*(math.pow(0.3 , 1-x)) *(math.pow(0.7 , 5-(1-x)))
s = a*b
sume += s
print('P(x = {} , y = {}) , s : {}'.format(x , 1-x , s))
print(sume)
print(1- len(list(itertools.combinations(np.arange(5) , 0)))*(math.pow(0.3 , 0)) *(math.pow(0.7 , 5))**2)P(X+Y = 1 ) = 0.1210
P(X+Y >= 1) = 0.9717
3. 이항분포의 평균과 분산
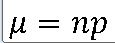
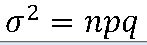
EX-01> A,B 공장 불량률 5% , 10 대의 TV에 포함된 불량품 수의 평균과 표준편차
n = 10 p = 0.05 q = 0.95
print(10 * 0.05)
print(math.sqrt(0.5 * 0.95))m = 5
s = 0.6892
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 이산확률변수' 카테고리의 다른 글
| ★초기하분포★기하분포★이산균등분포★기초통계학-[Chapter05 - 이산확률분포-06] (0) | 2022.12.15 |
|---|---|
| ★Seaborn에서의 Subplots★이항확률의 근사 확률★푸아송분포★기초통계학-[Chapter05 - 이산확률분포-05] (0) | 2022.12.15 |
| 푸아송분포★기초통계학-[Chapter05 - 이산확률분포-04] (0) | 2022.12.14 |
| 표본,모표본★평균과 분산★기초통계학-[Chapter05 - 이산확률분포-02] (0) | 2022.12.14 |
| ★key, value , items() , sorted(key =), loc로 행추가!★확률분포★기초통계학-[Chapter05 - 이산확률분포-01] (0) | 2022.12.14 |
표본,모표본★평균과 분산★기초통계학-[Chapter05 - 이산확률분포-02]
1. 평균
==> 이산확률변수의 확률 히스토그램 ==> 상대도수히스토그램과 유사
But. 상대도수히스토그램은 n개의 자료 값에 대한 표본 설명
확률 히스토그램은 실험에서 발생할 수 있는 모든 경우에 대하여 설명
https://knowallworld.tistory.com/202
★zip, collections.Counter()★도수표, 도수막대그래프★Plt, Fig, Seaborn 이해[Python]★기초통계학-[Chapter02
P46 고객 50명 대상으로 만족도 조사 GASAAIPIIGASSGPASSISPIPPPGASPIGIAGGSPASGPIAAGSSGGS ==> 50명의 고객 1. 도수표 그리기 c = 'GASAAIPIIGASSGPASSISPIPPPGASPIGIAGGSPASGPIAAGSSGGS' d = [] for i in c: d.append(i) d d = ['G', 'A','S', ···
knowallworld.tistory.com
==> 참고


E(X) ==> (0 * 1 + 1 * 3 + 2 * 3 + 3 * 1) / 8 = 12 / 8 = 3 /2 = 1.5

E(X) ==> (0 * 0.125 + 1 * 0.375 + 2 * 0.375 + 3 * 0.125) / 8 = 1.5 / 8 = 0.1875
2. 분산
width = ['{} ~ {}'.format(i+0.5 , i+10.5) for i in range(9,68 , 10)]
x_i = [ round((i+0.5 - 5),1) for i in range(19, 70, 10)]
dosu = [9,9,9,10,2,1]
print(len(dosu))
print(len(x_i))
A = pd.DataFrame([dosu , x_i] , columns = width , index = ['도수(f_i)' , '계급값(x_i)'] )
A = A.T
A.index.names = ['계급 간격']
A['f_i_x_i'] = A['도수(f_i)'] * A['계급값(x_i)']
A.loc['합계'] = A[:].sum(axis=0)
A.iloc[-1,1] = '-'
A
https://knowallworld.tistory.com/214
★DDOF = 1★모/표본분산 , 모/표본표준편차★평균편차★기초통계학-[Chapter03 - 04]
산포의 척도 ==> 평균깊이가 1.2M인 강을 키가 1.7M인 사람이 걸어서 무사히 건널 수 있는지에 대해 생각 ==> 강의 평균 깊이가 1.2M 라는 뜻은 1.2M보다 작은 부분도 있지만 1.2M보다 깊은 곳도 있을 수
knowallworld.tistory.com
==> 표본분산, 표본표준편차 참고
B = pd.DataFrame([dosu] , columns = x_i)
B.index = ['P(X = x)']
B.loc['P(X = x)'] = B.loc['P(X = x)'] / 40
B


B = B.T
B = B.reset_index()
BB['x * p(x)'] = (B.loc[: , 'P(X = x)']) * B.loc[:, 'index']
B['x**2 * p(x)'] = (B.loc[: , 'P(X = x)']) * (B.loc[:, 'index']**2)
B.loc['합계']= B[:].sum(axis=0)
# B.iloc[-1,1] = '-'
avg = B.iloc[-1, -2]
B
var = B.iloc[-1,-1] - avg**2
var==> 분산 : 173.75
https://knowallworld.tistory.com/217
경험적규칙★체비쇼프 정리★기초통계학-[Chapter03 - 06]
100개의 자료에서 구간 1 : [x-s , x+s] 안에 69개의 자료가 들어있다. ==> 3 + 5 + 6 + 4 + 9 + 1 + 6 + 4 + 7 + 8 + 4 + 9 + 3 = 69 구간 2: [x-2s , x+2s] ==> 69 + (1+1+2+4+1+5 + 2 + 4 +0 + 2 + 2 +2 +1) = 96 구간 3 : [x-3s , x+3s] ==> 96+ 2
knowallworld.tistory.com
==> 체비쇼프 정리 참고
===> 경험적 규칙(Empirical rule)에 의하여 자료의 68%가 [ |x-s , |x+s] 안에있고,95%가 [ |x-2s , |x+2s] , 99.7%가 [|x-3s , |x+3s]안에들어있다.
==> 100 * ( 1 - (1/k**2) ) %
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 이산확률변수' 카테고리의 다른 글
| ★초기하분포★기하분포★이산균등분포★기초통계학-[Chapter05 - 이산확률분포-06] (0) | 2022.12.15 |
|---|---|
| ★Seaborn에서의 Subplots★이항확률의 근사 확률★푸아송분포★기초통계학-[Chapter05 - 이산확률분포-05] (0) | 2022.12.15 |
| 푸아송분포★기초통계학-[Chapter05 - 이산확률분포-04] (0) | 2022.12.14 |
| 이항분포식★이항실험★이항분포의 평균,분산★베르누이시행★기초통계학-[Chapter05 - 이산확률분포-03] (1) | 2022.12.14 |
| ★key, value , items() , sorted(key =), loc로 행추가!★확률분포★기초통계학-[Chapter05 - 이산확률분포-01] (0) | 2022.12.14 |
★key, value , items() , sorted(key =), loc로 행추가!★확률분포★기초통계학-[Chapter05 - 이산확률분포-01]
1. 확률 분포
==> 확률을 구하기 위한 어떤 실험이 시행되었을 때, 모든 실험 결과의 구성이 아닌 수치적인 양에 주목
==> 확률 실험에서 나타날 수 있는 개개의 결과에 관련된 수
EX)
1. 몇 번째 주사위를 던졌을때 특정 숫자의 눈이 나올때까지 던진 횟수
2. 동전 3번 던져서 앞면이 나온 횟수
==> X 를 앞면이 나온 횟수라고 지정
HHH -> X =3
THH HTH HHT -> X =2
HTT THT TTH -> X= 1
TTT -> X= 0
==> 상태공간(State Space) : X {0 , 1 , 2 ,3} ==> X가 취할 수 있는 모든 수들의 집합
==> X의 상태공간의 원소는 4개
==> X가 취할 수 있는 값을 셈 할 수 있다 ==> 이 확률 변수를 이산확률 변수
2. 이산확률 변수(Discrete Random Variable)
==> 상태공간이 유한개의 수로 구성되거나 무수히 많더라도 셈을 할 수 있는 개수의 확률변수
EX) 이산확률변수 여부 판단
1> X는 주사위를 2번 던져서 나온 두 눈의 합이다.
==> 이산확률 변수
2> X는 10번의 룰렛게임에서 숫자 36이 나온 횟수이다.
==> 이산확률 변수
3> X는 교체된 형광등이 수명을 다할 때까지 걸리는 시간이다.
==> 이산확률 변수 X ==> 셈할 수 없다? ==> [0, 무한대]
4> X는 아이가 셋인 가정에서의 남자아이의 수
==> 이산확률변수 ==> 애기들 0,1,2,3
5> X는 500원 짜리 동전 5개와 100원짜리 동전 3개 들어있는 주머니에서 임의로 꺼낸 동전 3개에 포함된 100원짜리 동전의 개수
==> 이산확률변수
6>X는 52장의 카드에서 비복원추출에 5장 뽑을 때, 뽑은 카드안에 있는 그림 카드의 수
==> 이산확률변수
7>X는 52장의 카드에서 복원추출에 의해 5장 뽑을 때, 뽑은 카드안에 있는 그림 카드의 수
==> 이산확률변수 ==> X가 1,2,3 되므로
8>X는 게임 프로그램을 완성할 때까지 걸린시간
==> 이산확률변수 X
3. 확률분포(Probability Distribution)
==> X가 취하는 개개의 값에 대응하는 확률을 나타내는 표나 함수 또는 그래프를 의미한다.
coin = itertools.product(np.arange(2) , repeat=3)
# 확률변수 x는 앞면(1)
b = []
for i in coin:
a = sorted(collections.Counter(i).most_common() , reverse=True)
if a[0][0] !=1:
b.append(0)
else:
b.append(a[0][1])
d = collections.Counter(b)
d = dict(sorted(d.items()))
print(d)
ky , val = [] , []
ky = list(d.keys())
val = list(d.values())
for k,v in d.items():
print(k)
print(v)
A = pd.DataFrame([val] , columns = ky , index = ['P(X = x)'])
A.columns.names = ['X']
A = A.T
A['P(X = x)'] = A['P(X = x)'] / 8
A.loc['합계'] = A[:].sum(axis=0) #행 추가
A = A.T
A
==> keys() , values() , items() , sorted( key = ) , 행추가시 loc[] 로 추가!

p(x) = 1/8 , x= 0 , 3
3/8 , x= 1 , 2
==> p(x)를 확률변수 X의 확률함수(Probability function)이라 한다.

EX) 주사위 2번 던져서 나온 두 눈의 합을 확률 변수 X라 할때 , X의 확률분포를 확률표와 확률 함수로 나타내기
a = np.arange(1,7).tolist()
print(a)
ratio = list(itertools.product(a, repeat = 2))
ratio2 = list(map(lambda x : x[0]+x[1] , ratio)) # lambda 할 때 map, filter, reduce ,apply 생각!
ratio2 = collections.Counter(ratio2)
ratio2 = dict(sorted(ratio2.items()))
for k, v in ratio2.items():
v = v/8
ratio2[k] = v
ratio2==>lambda 할 때 map, filter, reduce ,apply 생각!
{2: 0.125, 3: 0.250, 4: 0.375, 5: 0.500, 6: 0.625 , 7: 0.750, 8: 0.625, 9: 0.500, 10: 0.375, 11: 0.250, 12: 0.125}
val = ratio2.values()
ky = ratio2.keys()
A = pd.DataFrame(val , index = ky )
A= A.T
A.index = ['P(X = x)']
A.columns.names = ['X']
A
p(x) =
1/36 , x = 2 ,12
2/36 , x = 3 ,11
3/36 , x = 4,10
4/36 , x = 5 , 9
5/36 , x = 6 , 8
6/36 , x = 7
==> 확률 함수
4. 확률질량함수(Probability Mass Function)


EX) 신혼부부가 아이 3명을 갖고자 한다. 확률변수 X는 여자아이의 수
1> 상태공간 Sx를 구하시오.
child = ['여자' ,'남자']
#0이 여자 1이 남자
S_x = list(itertools.product(child , repeat = 3))
S_x
S_x =
[('여자', '여자', '여자'),
('여자', '여자', '남자'),
('여자', '남자', '여자'),
('여자', '남자', '남자'),
('남자', '여자', '여자'),
('남자', '여자', '남자'),
('남자', '남자', '여자'),
('남자', '남자', '남자')]
2> X의 확률변수 p(x)를 구하라.
#확률 변수 X는 여자
res = []
for girls in S_x:
girl = sorted(list(collections.Counter(girls).most_common()) , reverse=True)
if girl[0][0] != '여자':
res.append(0)
else:
res.append(girl[0][1])
# girl =list(map(lambda x : x if sorted(collections.Counter(girls).most_common(), reverse=True)[0][0]=='여자' else 0 , girls))
print(res)
res2 = collections.Counter(res)
res2 = dict(sorted(res2.items()))==> sorted(res2.items()) 주목!
ky = res2.keys()
val = res2.values()
A = pd.DataFrame([val] , columns = ky)
A.index = ['P(X = x)']
A.columns.names = ['X']
A
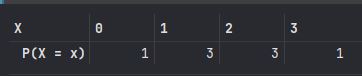
A.loc['P(X = x)'] = A.loc['P(X = x)'] /8
A
p(0) = 0.125 = 1/8
p(1) = 0.375 = 3/8
p(2) = 0.375 = 3/8
p(3) = 0.125 = 1/8
p(x) =
1/ 8 , x= 0,3
3/ 8 , x= 1 ,2
==> 확률함수
3> X의 확률질량함수 f(x)를 구하라.
f(x) =
1/8 , x = 0 ,3
3/8 , x = 1 , 2
0 , 다른곳에서
4> 적어도 2명 이상의 여자아이를 낳을 확률
P(X>=2) = 0.375 +0.125 = 0.5
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 이산확률변수' 카테고리의 다른 글
| ★초기하분포★기하분포★이산균등분포★기초통계학-[Chapter05 - 이산확률분포-06] (0) | 2022.12.15 |
|---|---|
| ★Seaborn에서의 Subplots★이항확률의 근사 확률★푸아송분포★기초통계학-[Chapter05 - 이산확률분포-05] (0) | 2022.12.15 |
| 푸아송분포★기초통계학-[Chapter05 - 이산확률분포-04] (0) | 2022.12.14 |
| 이항분포식★이항실험★이항분포의 평균,분산★베르누이시행★기초통계학-[Chapter05 - 이산확률분포-03] (1) | 2022.12.14 |
| 표본,모표본★평균과 분산★기초통계학-[Chapter05 - 이산확률분포-02] (0) | 2022.12.14 |
★lambda , filter★틀린것들 존재★기초통계학-[Chapter04 - 연습문제-04]
16. P(A) = 0.54 P(B) = 0.4 P(A M B) = 0.23 A회사나 B회사 제품만을 선호할 확률
P(B_c M A) = 0.54-0.23 = 0.31
P(A_c M B) = 0.4 - 0.23 = 0.17
0.31 + 0.17 = 0.48
17. 심장 박동이 정상이고, 저혈압인 환자가 선정될 확률
A = '고혈압'
B = '저혈압'
C = '혈압정상'
D = '심박 정상'
E = '심박비정상'
P(A) = 0.14
P(B) = 0.22
P(C) = 0.64
P(D) = 0.85
P(E) = 0.15
P(A|D) = 1/3 = P(A M D) / P(D) = P(A)P(D|A)
P(E|C) = 1/8 = P(E M C) / P(C)
P(D M C) = P(C)P(D|C) = P(D)P(C|D)
0.64 * P(D|C) = 0.85 * P(C|D)
18. 4명임의 선택 ,확률 구하기
Rh(+) O형은 27.3%
print(math.pow(0.273 , 4))
print(math.pow(0.727 , 4))
print(1- math.pow(0.727 , 4))
1> 4명이 모두 Rh(+) O형이다.
(27.3%)**4 = 0.00555
2>4명 중 그 누구도 Rh(+) O형이 아니다.
(72.7%)**4 = 0.2793
3>적어도 1명이 Rh(+)O 형이다.
1-(72.7%)**4 = 0.7206
19. 5지선다형 3문제
1> 3문제중 어느 하나를 맞을 확률
a = np.arange(2)
b = itertools.product(a, repeat= 3)
print(list(itertools.product(a, repeat= 3)))
c = list(filter(lambda x : collections.Counter(x).most_common()[0][0] == 0 and collections.Counter(x).most_common()[0][1] ==2 , b))
print(c)
print( len(c) * (1/5)*(4/5)*(4/5) )[(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1)]
[(0, 0, 1), (0, 1, 0), (1, 0, 0)]
0.3840000000000001
2> 처음 2문제를 맞을 확률
1/5 * 1/5 = 0.04
3> 모두 다 틀릴 확률
1 - 0.4879 = 0.5121
4>적어도 하나를 맞을 확률
1- (4/5)**3 = 0.4879
5> 정확히 한 문제를 맞았다고 할때 , 맞은 문제가 2번째 문제일 확률
b = itertools.product(a, repeat= 3)
e = list(filter(lambda x : collections.Counter(x).most_common()[0][0] ==1 and collections.Counter(x).most_common()[0][1] ==2 and x[1] == 1, b))
print(e)
print( len(e) * (1/5)*(4/5))[(0, 1, 1), (1, 1, 0)]
0.32000000000000006
20. 비복원 추출에 의한 3명의 학생 무작위 선정 ==> 남학생의 수가 여학생의 수보다 많을 확률
man = [i for i in range(8)]
girl = [j for j in range(8,15)]
#P(man > girl)
a = np.arange(2)
b = itertools.combinations_with_replacement(a , 3)
c = list(filter(lambda x : collections.Counter(x).most_common()[0][0] == 0 , b))
d=0
for i in c:
print(i)
d += len(list(itertools.combinations(np.arange(8) , collections.Counter(i).most_common()[0][1])))* len(list(itertools.combinations(np.arange(7) , (3-collections.Counter(i).most_common()[0][1]))))
print(d)
e = d/ len(list(itertools.combinations(np.arange(15) , 3)))
print(e)(0, 0, 0)
56
(0, 0, 1)
252
0.5538461538461539
0.5384615384615384
0이 남자 , 1이 여자
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 순열,조합' 카테고리의 다른 글
| ★lambda , filter★기초통계학-[Chapter04 - 연습문제-03] (1) | 2022.12.12 |
|---|---|
| ★lambda , filter★기초통계학-[Chapter04 - 연습문제-02] (0) | 2022.12.12 |
| ★collections.Counter()★itertools.groupby()★순열,조합 , 중복조합 , 중복순열★기초통계학-[Chapter04 - 연습문제-01] (0) | 2022.12.12 |
| ★전확률 공식★베이즈 정리★기초통계학-[Chapter04 - 확률-06] (0) | 2022.12.12 |
| ★독립사건 종속사건★조건부 확률★기초통계학-[Chapter04 - 확률-05] (0) | 2022.12.12 |
★lambda , filter★기초통계학-[Chapter04 - 연습문제-03]
11. 룰렛게임
13. 주사위 4번 던질 때, 처음 수가 1이 아닐 확률:
a = np.arange(1,7)
b= list(itertools.product(a, repeat = 4))
print(len(b))
c = list(filter(lambda x : x[0] != 1 , b))
print(len(c))print(round(1080 /1296,2))==> 0.83
14. 4명으로 구성된 그룹에서 적어도 2명의 생일이 같은 요일일 확률
days = np.arange(1,8)
a = list(itertools.product(days , repeat = 4))
b = list(filter(lambda x : collections.Counter(x).most_common()[0][1] >=2 , a))
print(round(len(b) / len(a) , 2))==> 0.65
15. 5명이 방안에 있다. 이들 중 생일이 같은 사람이 2명이상일 확률
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 순열,조합' 카테고리의 다른 글
| ★lambda , filter★틀린것들 존재★기초통계학-[Chapter04 - 연습문제-04] (0) | 2022.12.13 |
|---|---|
| ★lambda , filter★기초통계학-[Chapter04 - 연습문제-02] (0) | 2022.12.12 |
| ★collections.Counter()★itertools.groupby()★순열,조합 , 중복조합 , 중복순열★기초통계학-[Chapter04 - 연습문제-01] (0) | 2022.12.12 |
| ★전확률 공식★베이즈 정리★기초통계학-[Chapter04 - 확률-06] (0) | 2022.12.12 |
| ★독립사건 종속사건★조건부 확률★기초통계학-[Chapter04 - 확률-05] (0) | 2022.12.12 |
★lambda , filter★기초통계학-[Chapter04 - 연습문제-02]
※표본공간이란 ? 모든 결과들의 집합 의미
5. 표본공간 구하기
1> '1'의 눈이 나올 때까지 공정한 주사위를 반복하여 던진 횟수
{1,2,3,4,·······················}
2> 최저 온도 21˙C 에서 최고 온도 32.3˙C까지 24시간 동안 연속적으로 기록된 온도게 눈금의 위치
6. 여학생 A,B,C 남학생 D,E 중 2명의 과대표와 총무 선출
1> 표본공간
man = ['상국' , '영훈']
woman = ['연주' , '하나' , '채은']
man_woman = man + woman
Sample_space = list(itertools.combinations( man_woman , 2))
print(len(Sample_space))
Sample_space==> 리스트 끼리 더하면 추가된다!!!
==> 20
==>
[('상국', '영훈'),
('상국', '연주'),
('상국', '하나'),
('상국', '채은'),
('영훈', '연주'),
('영훈', '하나'),
('영훈', '채은'),
('연주', '하나'),
('연주', '채은'),
('하나', '채은')], ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥ ‥
2> 영훈이가 과대표
d = list(filter(lambda x : x[0] in '영훈' , Sample_space))
d[('영훈', '상국'), ('영훈', '연주'), ('영훈', '하나'), ('영훈', '채은')]
3> 채은이가 총무
d = list(filter(lambda x : x[1] in '채은' , Sample_space))
d[('상국', '채은'), ('영훈', '채은'), ('연주', '채은'), ('하나', '채은')]
4> 여학생이 과대표와 총무
d = list(filter(lambda x : x[0] in woman and x[1] in woman , Sample_space))
d[('연주', '하나'), ('연주', '채은'), ('하나', '연주'), ('하나', '채은'), ('채은', '연주'), ('채은', '하나')]
7. 확률
1> P(A) = 1/4 , P(B) = 1/3 ,P(A U B) = 1/2 ==> P(A M B) = (1/4 + 1/3) -(1/2) = 7/12 - 6/12 = 1/12
2> P(A) = 1/3 , P(A M B) = 1/12 , P(A U B) = 1/2 ==> P(B) = 1/2 - (1/3) + 1/12 = 6/12 - 4/12 + 1/12 = 3 /12= 1/4
3> S = (A U B) , P(A) = 0.75 , P(B) = 0.63 , P(A M B) ==> 0.75 + 0.63 -1 = 1.38 - 1 = 0.38
4> P(A) = 0.3 , P(B) = 0.5 , P(A M B_c) = 0.2 ==> P(A_c M B_c) = P(A U B)_c = 0.3
P(A U B ) = 0.3 +0.5 - 0.1 = 0.7
P(A M B) = 0.1
5> P(A) = 0.3 , P(A M B) = 0.1 ==> P(A|B) = P(A M B) / P(B) = 0.1/0.8
P(B_c M A) = 0.2 = P(A) P(B_c | P(A)) = 0.2
P(B | A ) = P(A M B ) / P(A) = 1 /3
8. 앞면이 나올 가능성이 2/3 인 찌그러진 동전 2번 던질때
1> 앞면이 한 번도 안나올 확률
P(A) = 2/3
P(B) = 1/3
==> 독립 사건
P(B) * P(B) = 1/9
2> 앞면이 한 번 나올 확률
1 - (1/9 + 4/9) = 1 - 5/9 = 4/9
3> 앞면이 두 번 나올 확률
P(A) * P(A) = 2/3 * 2/3 = 4/9
9. 초등학교 500가구의 확률
a = [9, 11 ,28 , 35 , 48 , 215 , 132 ,22]
A = pd.DataFrame([a] , columns=[0,1,2,3,4,5,6,'7이상'] , index = ['식사 횟수' , '가구 수'])
A['합계'] = A[:].sum(axis=1)
A
1> 집에서 가족 전체가 식사를 한번도 하지 못할 확률
9/500 = 0.018
2>가족 전체가 적어도 3번 식사할 확률 [P(X>=3)] = (500- 9 - 11 -28) / 500 =
452 /500 = 0.904
3> 가족 전체가 많아야 3번 식사할 확률 [P(X<=3)] = (9+11+28+35) /500 = 83/500 = 0.166
10. 표본조사 확률
A = [4,6,13,16,10,0,1]
cols = ['{}~{}'.format(i+0.5 , i+9.5) for i in range(9 , 72 , 9) ]
print(cols)
A = pd.DataFrame([A] , index = ['사용시간'] , columns=cols)
A.columns.names = ['사용시간']
A.index = ['인원수']
A
1> 인터넷을 27.5 시간 이하로 사용할 확률 : 10/ 50 = 0.2
2>인터넷을 18.5 이상, 45.5 이하로 사용할 확률 : 6+ 13 +16 / 50 = 35 /50 = 0.7
3> 인터넷을 45.5이상 사용할 확률 : 11/50 = 0.22
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 순열,조합' 카테고리의 다른 글
| ★lambda , filter★틀린것들 존재★기초통계학-[Chapter04 - 연습문제-04] (0) | 2022.12.13 |
|---|---|
| ★lambda , filter★기초통계학-[Chapter04 - 연습문제-03] (1) | 2022.12.12 |
| ★collections.Counter()★itertools.groupby()★순열,조합 , 중복조합 , 중복순열★기초통계학-[Chapter04 - 연습문제-01] (0) | 2022.12.12 |
| ★전확률 공식★베이즈 정리★기초통계학-[Chapter04 - 확률-06] (0) | 2022.12.12 |
| ★독립사건 종속사건★조건부 확률★기초통계학-[Chapter04 - 확률-05] (0) | 2022.12.12 |