★key, value , items() , sorted(key =), loc로 행추가!★확률분포★기초통계학-[Chapter05 - 이산확률분포-01]
1. 확률 분포
==> 확률을 구하기 위한 어떤 실험이 시행되었을 때, 모든 실험 결과의 구성이 아닌 수치적인 양에 주목
==> 확률 실험에서 나타날 수 있는 개개의 결과에 관련된 수
EX)
1. 몇 번째 주사위를 던졌을때 특정 숫자의 눈이 나올때까지 던진 횟수
2. 동전 3번 던져서 앞면이 나온 횟수
==> X 를 앞면이 나온 횟수라고 지정
HHH -> X =3
THH HTH HHT -> X =2
HTT THT TTH -> X= 1
TTT -> X= 0
==> 상태공간(State Space) : X {0 , 1 , 2 ,3} ==> X가 취할 수 있는 모든 수들의 집합
==> X의 상태공간의 원소는 4개
==> X가 취할 수 있는 값을 셈 할 수 있다 ==> 이 확률 변수를 이산확률 변수
2. 이산확률 변수(Discrete Random Variable)
==> 상태공간이 유한개의 수로 구성되거나 무수히 많더라도 셈을 할 수 있는 개수의 확률변수
EX) 이산확률변수 여부 판단
1> X는 주사위를 2번 던져서 나온 두 눈의 합이다.
==> 이산확률 변수
2> X는 10번의 룰렛게임에서 숫자 36이 나온 횟수이다.
==> 이산확률 변수
3> X는 교체된 형광등이 수명을 다할 때까지 걸리는 시간이다.
==> 이산확률 변수 X ==> 셈할 수 없다? ==> [0, 무한대]
4> X는 아이가 셋인 가정에서의 남자아이의 수
==> 이산확률변수 ==> 애기들 0,1,2,3
5> X는 500원 짜리 동전 5개와 100원짜리 동전 3개 들어있는 주머니에서 임의로 꺼낸 동전 3개에 포함된 100원짜리 동전의 개수
==> 이산확률변수
6>X는 52장의 카드에서 비복원추출에 5장 뽑을 때, 뽑은 카드안에 있는 그림 카드의 수
==> 이산확률변수
7>X는 52장의 카드에서 복원추출에 의해 5장 뽑을 때, 뽑은 카드안에 있는 그림 카드의 수
==> 이산확률변수 ==> X가 1,2,3 되므로
8>X는 게임 프로그램을 완성할 때까지 걸린시간
==> 이산확률변수 X
3. 확률분포(Probability Distribution)
==> X가 취하는 개개의 값에 대응하는 확률을 나타내는 표나 함수 또는 그래프를 의미한다.
coin = itertools.product(np.arange(2) , repeat=3)
# 확률변수 x는 앞면(1)
b = []
for i in coin:
a = sorted(collections.Counter(i).most_common() , reverse=True)
if a[0][0] !=1:
b.append(0)
else:
b.append(a[0][1])
d = collections.Counter(b)
d = dict(sorted(d.items()))
print(d)
ky , val = [] , []
ky = list(d.keys())
val = list(d.values())
for k,v in d.items():
print(k)
print(v)
A = pd.DataFrame([val] , columns = ky , index = ['P(X = x)'])
A.columns.names = ['X']
A = A.T
A['P(X = x)'] = A['P(X = x)'] / 8
A.loc['합계'] = A[:].sum(axis=0) #행 추가
A = A.T
A
==> keys() , values() , items() , sorted( key = ) , 행추가시 loc[] 로 추가!

p(x) = 1/8 , x= 0 , 3
3/8 , x= 1 , 2
==> p(x)를 확률변수 X의 확률함수(Probability function)이라 한다.

EX) 주사위 2번 던져서 나온 두 눈의 합을 확률 변수 X라 할때 , X의 확률분포를 확률표와 확률 함수로 나타내기
a = np.arange(1,7).tolist()
print(a)
ratio = list(itertools.product(a, repeat = 2))
ratio2 = list(map(lambda x : x[0]+x[1] , ratio)) # lambda 할 때 map, filter, reduce ,apply 생각!
ratio2 = collections.Counter(ratio2)
ratio2 = dict(sorted(ratio2.items()))
for k, v in ratio2.items():
v = v/8
ratio2[k] = v
ratio2==>lambda 할 때 map, filter, reduce ,apply 생각!
{2: 0.125, 3: 0.250, 4: 0.375, 5: 0.500, 6: 0.625 , 7: 0.750, 8: 0.625, 9: 0.500, 10: 0.375, 11: 0.250, 12: 0.125}
val = ratio2.values()
ky = ratio2.keys()
A = pd.DataFrame(val , index = ky )
A= A.T
A.index = ['P(X = x)']
A.columns.names = ['X']
A
p(x) =
1/36 , x = 2 ,12
2/36 , x = 3 ,11
3/36 , x = 4,10
4/36 , x = 5 , 9
5/36 , x = 6 , 8
6/36 , x = 7
==> 확률 함수
4. 확률질량함수(Probability Mass Function)
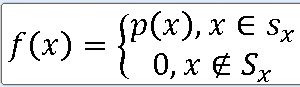

EX) 신혼부부가 아이 3명을 갖고자 한다. 확률변수 X는 여자아이의 수
1> 상태공간 Sx를 구하시오.
child = ['여자' ,'남자']
#0이 여자 1이 남자
S_x = list(itertools.product(child , repeat = 3))
S_x
S_x =
[('여자', '여자', '여자'),
('여자', '여자', '남자'),
('여자', '남자', '여자'),
('여자', '남자', '남자'),
('남자', '여자', '여자'),
('남자', '여자', '남자'),
('남자', '남자', '여자'),
('남자', '남자', '남자')]
2> X의 확률변수 p(x)를 구하라.
#확률 변수 X는 여자
res = []
for girls in S_x:
girl = sorted(list(collections.Counter(girls).most_common()) , reverse=True)
if girl[0][0] != '여자':
res.append(0)
else:
res.append(girl[0][1])
# girl =list(map(lambda x : x if sorted(collections.Counter(girls).most_common(), reverse=True)[0][0]=='여자' else 0 , girls))
print(res)
res2 = collections.Counter(res)
res2 = dict(sorted(res2.items()))==> sorted(res2.items()) 주목!
ky = res2.keys()
val = res2.values()
A = pd.DataFrame([val] , columns = ky)
A.index = ['P(X = x)']
A.columns.names = ['X']
A

A.loc['P(X = x)'] = A.loc['P(X = x)'] /8
A
p(0) = 0.125 = 1/8
p(1) = 0.375 = 3/8
p(2) = 0.375 = 3/8
p(3) = 0.125 = 1/8
p(x) =
1/ 8 , x= 0,3
3/ 8 , x= 1 ,2
==> 확률함수
3> X의 확률질량함수 f(x)를 구하라.
f(x) =
1/8 , x = 0 ,3
3/8 , x = 1 , 2
0 , 다른곳에서
4> 적어도 2명 이상의 여자아이를 낳을 확률
P(X>=2) = 0.375 +0.125 = 0.5
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 이산확률변수' 카테고리의 다른 글
| ★초기하분포★기하분포★이산균등분포★기초통계학-[Chapter05 - 이산확률분포-06] (0) | 2022.12.15 |
|---|---|
| ★Seaborn에서의 Subplots★이항확률의 근사 확률★푸아송분포★기초통계학-[Chapter05 - 이산확률분포-05] (0) | 2022.12.15 |
| 푸아송분포★기초통계학-[Chapter05 - 이산확률분포-04] (0) | 2022.12.14 |
| 이항분포식★이항실험★이항분포의 평균,분산★베르누이시행★기초통계학-[Chapter05 - 이산확률분포-03] (1) | 2022.12.14 |
| 표본,모표본★평균과 분산★기초통계학-[Chapter05 - 이산확률분포-02] (0) | 2022.12.14 |