전체 글
★scipy.stats.t(자유도).ppf()★t-분포★기초통계학-[Chapter06 - 연속확률분포-07]
1. T-분포(Chi-square Distribution)
==> T-분포는 모분산이 알려지지 않은 정규모집단의 모평균에 대한 추론
==>서로 독립인 표준정규화확률변수 Z와 자유도 n인 카이제곱 확률변수 V에 대하여 정의
==> T ~ t(n)으로 나타낸다.


==>분포 곡선은 t=0에서 최대값을 갖고 , 대칭 ==> 평균, 중위수 , 최빈값이 동일
==> 표준정규분포와 같이 종 모양
X = np.arange(-5,5 , .1)
fig = plt.figure(figsize=(15,8))
dof_2 = []
for dof in np.arange(1 , 10 , 3)+1:
ax = sns.lineplot(x = X , y=scipy.stats.t(dof).pdf(X) )
dof_2.append(dof)
ax2 = sns.lineplot(x=X , y=scipy.stats.norm.pdf(X) , color = 'red')
b = ['t-(n={})'.format(i) for i in dof_2]
b.append('N(0,1)')
plt.legend(b , fontsize = 15)==> scipy.stats.t.pdf()활용!!!
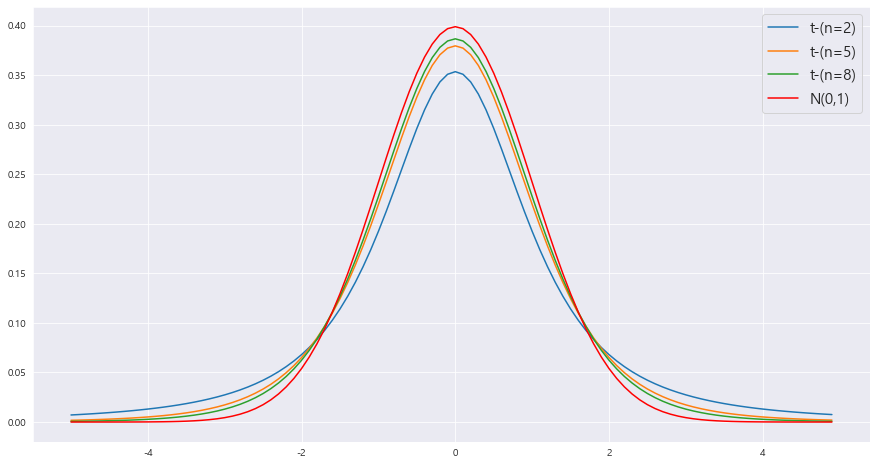
==> t-분포의 꼬리 부분이 표준정규분포보다 약간 두텁다.
==>자유도 n이 증가하면 t-분포는 표준정규분포에 근접
EX-01) 자유도 10인 T-분포에서 중심확률이 0.9인 두 임계점 t_L , t_R
==> 꼬리확률 5%
X = np.arange(-5,5 , .1)
fig = plt.figure(figsize=(15,8))
dof_2 = [10]
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
t_r = scipy.stats.t(dof_2).ppf(0.95)
print(t_r)
t_l = scipy.stats.t(dof_2).ppf(0.05)
print(t_l)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X<=t_r) & (X>=t_l) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
ax.vlines(x = t_l ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_l) , colors = 'black')
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.text(1.71 , .17, r'$P(T>t_{-0.05})$' + f'= {0.90}',fontsize=15)
ax.text(t_l + 0.25 , 0.02 , r'$t_l$' + f'= {t_l}' , fontsize = 13 )
ax.text(t_r - 1 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
T_l = -1.812
T_r = 1.812
EX-02) 자유도 4인 t-분포
1>P(T> t_0.025) = 0.025를 만족하는 임계값 t_0.025
P(T<= t_0.025) = 1 - 0.025
X = np.arange(-5,5 , .01)
fig = plt.figure(figsize=(15,8))
dof_2 = [4]
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
t_r = scipy.stats.t(dof_2).ppf(1- 0.025)
print(t_r)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
plt.annotate('' , xy=(3.5, .007), xytext=(2.5 , .16) , arrowprops = dict(facecolor = 'black'))
ax.text(1.71 , .17, r'$P(T>t_{0.025})$' + f'= {0.025}',fontsize=15)
ax.text(t_r - 1 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
t_0.025 = 2.776
2>P(|T|< t_0) = 0.99를 만족하는 임계값 t_0
꼬리확률 = 0.005
X = np.arange(-5,5 , .01)
fig = plt.figure(figsize=(15,8))
dof_2 = [4]
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
t_r = scipy.stats.t(dof_2).ppf(0.995)
print(t_r)
t_l = scipy.stats.t(dof_2).ppf(0.005)
print(t_l)
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) | (X<=t_l) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
ax.vlines(x = t_l ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_l) , colors = 'black')
plt.annotate('' , xy=(4.5, .007), xytext=(3.5 , .16) , arrowprops = dict(facecolor = 'black'))
ax.text(1.71 , .17, r'$P(T>t_{0})$' + f'= {0.005}',fontsize=15)
ax.text(t_l + 0.25 , 0.02 , r'$t_l$' + f'= {t_l}' , fontsize = 13 )
ax.text(t_r + 0.21 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
t_0 = 4.604
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 연속확률변수' 카테고리의 다른 글
★scipy.stats.chi2().ppf()★matplotlib 수학식표현★카이제곱분포★정규분포★기초통계학-[Chapter06 - 연속확률분포-06]
1. 카이제곱분포
==> 카이제곱분포는 정규모집단의 모분산에 대한 통계적 추론에 사용
==> n개의 서로 독립인 표준정규확률변수 Z_1 ,Z_2 ,···· Z_n 에 대하여 확률변수의 확률분포를 자유도(degree of freedom) , d.f. = n인 카이제곱분포
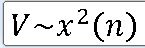

X = np.linspace(0.5 , 50 , 100)
fig = plt.figure(figsize=(15,8))
a = [1,2,3,4,5,10,20,30]
for dof in a:
sns.lineplot(X , scipy.stats.chi2(dof).pdf(X))
b = [r'$\chi^2(\eta$ = {})'.format(i) for i in a]
print(b)
plt.legend(b , fontsize = 15)==> matplotlib 수학식 표현!!!
https://codetorial.net/matplotlib/mathematical_expressions.html
Matplotlib 수학적 표현 사용하기 - Codetorial
6) 표준 함수 (Standard Functions)와 대형 기호 (Big Symbols) 아래 그림과 같이 Matplotlib에서 삼각함수 (sin, cos, tan 등), 극한 (lim), 최대 (max), 최소 (min) 등의 표현과 다양한 대형 연산자 기호를 사용할 수 있
codetorial.net

==> 자유도 n이 커질수록 종 모양의 분포에 가까워진다.
==> n이 커질수록 카이제곱 분포는 정규분포에 근사한다.
EX-01) 자유도 10인 카이제곱분포에서 왼쪽 꼬리확률과 오른쪽 꼬리확률이 각가 5%인 두 임계점을 구하라.
d.f = 10
P(V> x_L**2) = 0.95
matplotlib.rc("font" , family = "Times New Roman" , weight = "bold")
X = np.arange(0,30,.1)
fig = plt.figure(figsize=(15,8))
dof = 10 #자유도
ax = sns.lineplot(X , scipy.stats.chi2(dof).pdf(X)) #18.31 , 3.94 어케?
#P(X>X_r) = 0.05
#P(X<=X_r) = 0.95
X_r = scipy.stats.chi2(dof).ppf(0.95) #==> 1.644
#X_r = 10 + math.sqrt(20)*1.644 #평균 = n , 분산 = 2n
print(X_r)
#P(X<X_l) = 0.05
X_l = scipy.stats.chi2(dof).ppf(0.05) #==> 1.644
print(X_l)
ax.fill_between(X, scipy.stats.chi2(dof).pdf(X) , where = (X>=X_r) | (X<=X_l) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = 1- scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(25 , .015, 'P(X >' + r'$\chi^2_{0.05}$)' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(22, .002), xytext=(24 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= X_l, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_l) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
area = scipy.stats.chi2(dof).cdf(X_l) #넓이 구하기!!!!!
ax.text(-1 , .02, 'P(X >' + r'$\chi^2_{0.05}$)' + f"= {round(area,4)}",fontsize=15)
ax.text(X_l + 1, .02, r'$\chi^2_L= {}$'.format(round(X_l,2)) ,fontsize=15)
ax.text(X_r - 3.5, .01, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
plt.annotate('' , xy=(2.5, .002), xytext=(0 , .014) , arrowprops = dict(facecolor = 'black'))
b = [r'$\chi^2(\eta$ = {})'.format(i) for i in a]
print(b)
plt.legend(b , fontsize = 15)==> scipy.stats.chi2(자유도).ppf(꼬리확률) ==> X_l , X_R 값 구할 수 있게 된다!

EX-02) 확률변수 V가 자유도 5인 카이제곱분포에서 P(V<x_0) = 0.95를 만족하는 임계값 x_0를 구하라.
matplotlib.rc("font" , family = "Times New Roman" , weight = "bold")
X = np.arange(0,30,.1)
fig = plt.figure(figsize=(15,8))
dof = 5 #자유도
ax = sns.lineplot(X , scipy.stats.chi2(dof).pdf(X)) #18.31 , 3.94 어케?
#P(X>X_r) = 0.05
#P(X<=X_r) = 0.95
X_r = scipy.stats.chi2(dof).ppf(0.95)
#X_r = 10 + math.sqrt(20)*1.644 #평균 = n , 분산 = 2n
print(X_r)
ax.fill_between(X, scipy.stats.chi2(dof).pdf(X) , where = (X<=X_r) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
area = scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(10 , .08, 'P(X <=' + r'$\chi^2_{0.95}$)' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(7, .06), xytext=(10 , .08) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 3.5, .01, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)
b = [r'$\chi^2(\eta$ = {})'.format(dof)]
print(b)
plt.legend(b , fontsize = 15)
x_0 = 11.07
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 연속확률변수' 카테고리의 다른 글
| ★scipy.stats.f(자유도1 , 자유도 2).pdf()★F-분포★기초통계학-[Chapter06 - 연속확률분포-08] (0) | 2022.12.23 |
|---|---|
| ★scipy.stats.t(자유도).ppf()★t-분포★기초통계학-[Chapter06 - 연속확률분포-07] (0) | 2022.12.23 |
| 이항분포, 푸아송분포,정규분포 기억하기★cdf, pdf 사용법!★정규근사★파스칼★이항분포의 정규근사★기초통계학-[Chapter06 - 연속확률분포-05] (0) | 2022.12.22 |
| ★정규분포의 표준정규분포로의 변환★추측통계학-[Chapter06 - 연속확률분포-04] (0) | 2022.12.22 |
| 정규분포의 표준정규분포로의 변환★기초통계학-[Chapter06 - 연속확률분포-03] (0) | 2022.12.20 |
이항분포, 푸아송분포,정규분포 기억하기★cdf, pdf 사용법!★정규근사★파스칼★이항분포의 정규근사★기초통계학-[Chapter06 - 연속확률분포-05]
1.이항분포의 정규근사
==> 매회 성공률인 P인 이항 실험을 n번 독립적으로 반복하여 시행할 때 성공의 횟수 ==> 이항분포
https://knowallworld.tistory.com/241
이항분포식★이항실험★이항분포의 평균,분산★베르누이시행★기초통계학-[Chapter05 - 이산확률
1. 이항분포 ==> 많이 사용하는 확률 모형 : 이항분포, 푸아송분포 , 초기하분포 1. 이항실험(Bionomial Experiment) ==> 실험은 N번의 시행 ==> 실험 결과는 성공(S) , 실패(F) ==> 성공 확률 : p , 실패 확률 : q
knowallworld.tistory.com
==> 이항분포
==>시행횟수 n이 충분히 크면 누적이항확률표 이용
==> np<= 5인 경우 푸아송분포 이용하여 근사적으로 이항확률 구함.
https://knowallworld.tistory.com/242
푸아송분포★기초통계학-[Chapter05 - 이산확률분포-04]
1.푸아송 분포 ==> 이항분포에 대한 확률을 계산하기 위하여 누적이항확률표 사용 ==> but. 시행(n)이 30보다 큰 경우의 확률표 X ==> 시행(n)이 30보다 클 경우의 확률 근사값 구할 수 있다. 1> 확률 실
knowallworld.tistory.com
==> n이 충분히 크면서도 성공률 p가 충분히 작지 않은 경우, 푸아송 분포 사용이 어렵다.
==> 이항분포
from scipy.stats import binom
data_binom = binom(n=50 , p=0.7)
sample_binom=data_binom.rvs(1000) ## 생성된 분포 기반 1000개의 Sample 생성
## Counter 함수를 활용하여 성공횟수(x)별 횟수 도출 및 데이터 프레임 변환
count = collections.Counter(sample_binom)
countCounter({32: 75, 34: 110, 31: 59,36: 118, 35: 126, 33: 91, ············
count_data = pd.DataFrame.from_dict(count, orient="index").reset_index()
count_data =count_data.rename(columns={"index":"number", 0:"count"})
count_data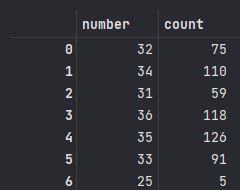
fig = plt.figure(figsize= (15,8))
## 시각화
ax = sns.barplot(x = count_data["number"], y= count_data["count"])
ax.set_xlabel("number of success")
ax.set_ylabel("x")
ax.set_title("Simulation Result")
plt.show()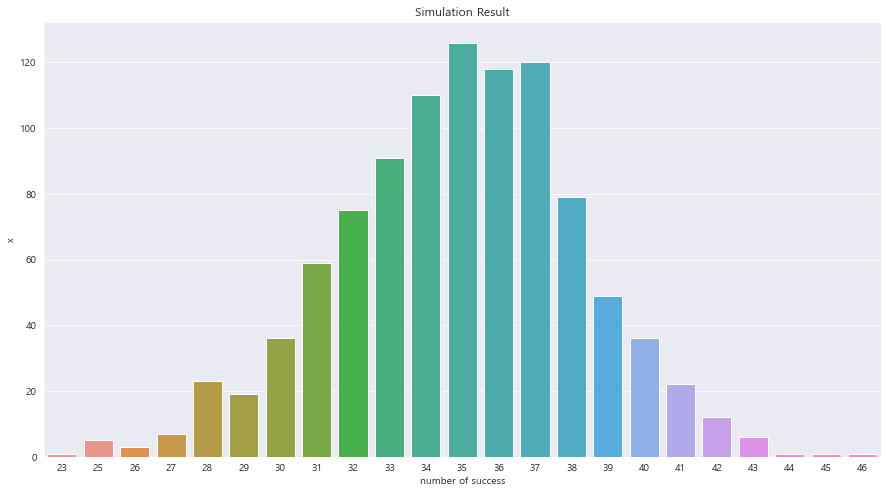
fig = plt.figure(figsize= (15,8))
## 시각화
ax = sns.histplot(sample_binom) #sample_binom으로 히스토그램 그리기
ax.set_xlabel("number of success")
ax.set_ylabel("x")
ax.set_title("Simulation Result")
plt.show()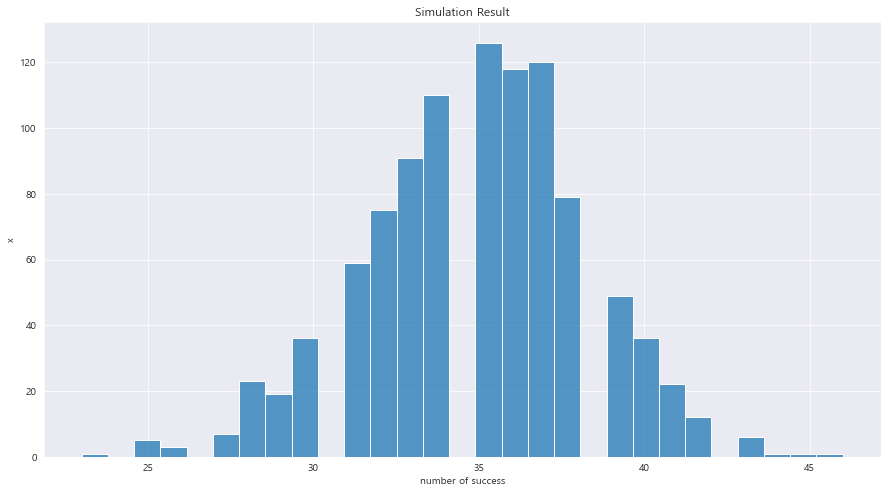
==> 근데 왜 비어있지?
fig = plt.figure(figsize= (15,8))
## 시각화
ax = sns.distplot(sample_binom)
ax.set_xlabel("number of success")
ax.set_ylabel("x")
ax.set_title("Simulation Result")
plt.show()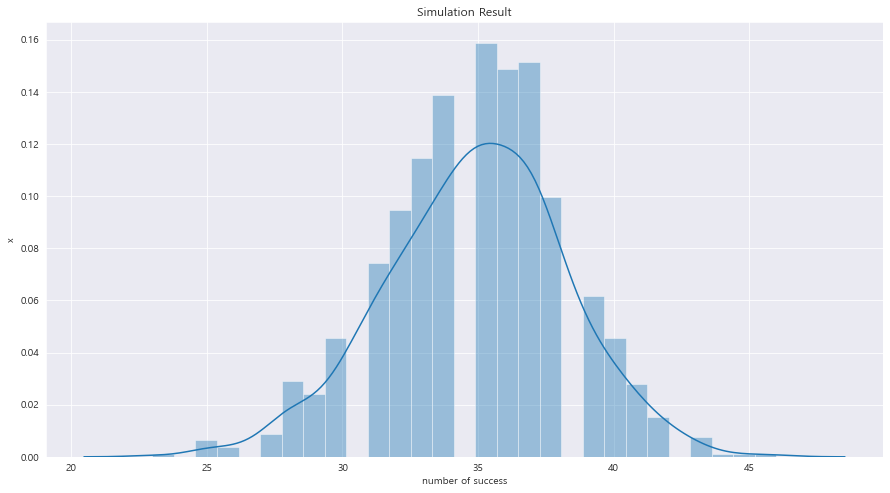
fig ,ax = plt.subplots(figsize=(15, 8))
## 시각화
ax = sns.lineplot(x= count_data['number'] , y=count_data['count'])
ax.set_xlabel("number of success")
ax.set_ylabel("x" , fontsize = 13 , rotation = 0)
ax.set_title("Simulation Result")
ax2 = ax.twinx() #한 그래프에 두번째 plot 넣기
ax2 = sns.histplot(sample_binom)
ax2.axes.yaxis.set_visible(False) #y축 없애기
plt.show()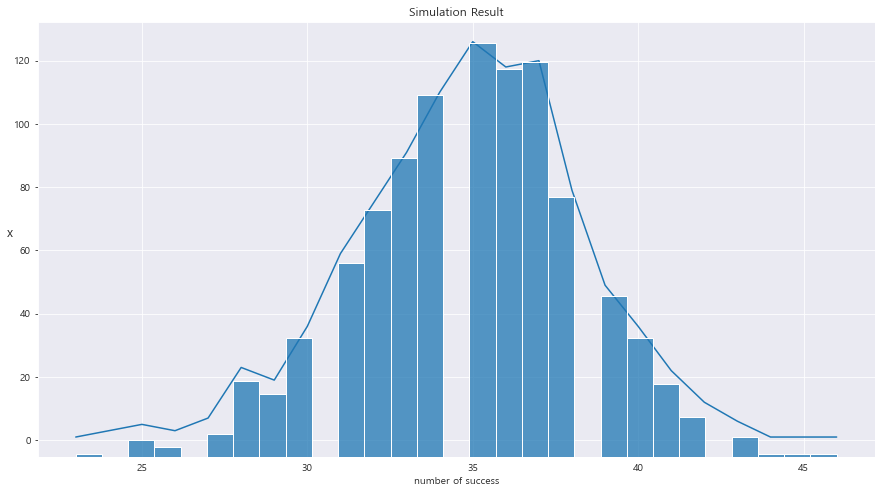
EX-01) 확률변수 X가 모수 n=50 , p = 0.7인 이항분포
1> 이항확률 P(33<=X<=39)
평균 : np = 35
분산 : npq = 10.5
㉠ 이항분포 : P(X<=39) - P(X<=32) = 50C39 * (0.7 ** 39) * (0.3 ** 11) - 50C32 * (0.7 ** 32) * (0.3 ** 18) =
==> 파스칼의 삼각형 참고!!
https://knowallworld.tistory.com/256
[PYTHON]_코테에서도 쓰일_조합_계산_파스칼의 삼각형(이항정리) 사용하기!!
1. itertools.combination 사용하기 https://knowallworld.tistory.com/146 [Python] 순열, 조합, 중복순열, 중복조합(itertools이용한 백트래킹) https://knowallworld.tistory.com/228 Permutations()★순열,조합,중복순열,중복조합★
knowallworld.tistory.com
result = 1
N = 50
K = [39 , 32]
P_X =[]
for t in K:
p_x = 0
for p in range(t+1):
result = 1
N = 50
for i in range(p):
result *= N
N -= 1
divisor = 1
for i in range(2, p+1):
divisor *= i
p_x += (result // divisor) * math.pow(0.7 , p) * math.pow(0.3 , 50-p)
P_X.append(p_x)
print("p_x : {}".format(p_x))
print(P_X[0] - P_X[1])==> 이항분포 정리는 P(X=1) + P(X=2) = P(X<=2) 이런식으로 가야한다!
p_x : 0.9211493751769412
p_x : 0.2178069383895617
0.7033424367873795
㉡ 푸아송분포 : P(X=39) = (평균(뮤) ** 39) * e **(-평균) / 39!
P(X=32) = (평균(뮤) ** 32) * e **(-평균) / 32!
f_x=0
for x in range(40):
f_x += math.pow(means,x) * math.exp(-means) / math.factorial(x)
print(f_x) # ==> 푸아송 분포0.7801904451746821
㉢ 정규분포(정규근사)
print(stats.norm.cdf(0.3809))
print(stats.norm.cdf(-0.2857))P(X<=39) = P(Z <= (39 - 35)/ 루트(10.5) ) = P (Z<= 1.2344) = 0.8914
P(X<=33) = P(Z <= (33 -35) / 루트(10.5) ) = P(Z<= -0.61721) = 0.2685
0.8914 - 0.2685 = 0.6229
EX-02) X ~B(15 , 0.4)
1> 확률 P(7<= X <=9)
㉠ 이항분포 : P(X<=9) - P(X<=7) ==> 이산확률분포
P(X=9) + P(X=8) + P(X=7) = 15C9 * (0.4 ** 9) * (0.6 ** 6) + ·········· = 0.3563
result = 1
K = [9,8,7]
res= []
for p in K:
result = 1
N = 15
for i in range(p):
result *= N
N -= 1
print('result : {}'.format(result))
print('N : {}'.format(N))
divisor = 1
for i in range(2, p+1):
divisor *= i
res.append(result//divisor * math.pow(0.4 ,p) * math.pow(0.6 ,15-p))
print(res)
print(sum(res))p_x : 0.2783785597956358
p_x : 0.05001254005377596
0.22836601974185985
㉡ 푸아송분포 : P(X=9) = (평균(뮤) ** 9) * e **(-평균) / 9!
P(X=7) = (평균(뮤) ** 7) * e **(-평균) / 7!
평균(뮤) = 15*0.4 = 6
분산 = 15 * 0.4 * 0.6 = 3.6
f_x=0
f_x_2 = 0
means = 6
vars = 3.6
for x in range(9+1):
f_x += math.pow(means,x) * math.exp(-means) / math.factorial(x)
for x in range(7+1):
f_x_2 += math.pow(means,x) * math.exp(-means) / math.factorial(x)
print(f_x) # ==> 푸아송 분포
print(f_x_2)
print(f_x - f_x_2)P(X<=9) = 0.916
P(X<=7) = 0.7439
P(7<=X<=9) = 0.1720
㉢ 정규분포(정규근사) ==> 연속확률분포
P( (7-6)/루트(3.6) <= Z <= (9-6)/루트(3.6) ) = P(0.527 <=Z <= 1.5811)
print(stats.norm.cdf(1.5811))
print(stats.norm.cdf(0.527))
print(0.943 - 0.7009)
P(Z<=1.5811) - P(Z<=0.527) = 0.9430 - 0.7009 = 0.2420
2. 정규근사에 의한 근사확률 ==> 연속성 수정 정규근사
==> 정규근사에 의한 근사 확률을 계산할때 , 누락된 부분을 없애기 위해 P(a-0.5 <= X <= b+0.5)를 구한다. ==> 오차를 줄일 수 있다.
EX-01)n = 50 , p = 0.7 , 연속성 수정한 정규근사에 의한 P(33<=X<=39)의 근사확률
P(33 - 0.5 <= X <= 39 +0.5) = P( Z<= (39.5 - 50) / 루트(50*0.7*0.3) ) - P( Z<=(32.5 - 50) / 루트(50*0.7*0.3) )
print(stats.norm.cdf(1.388))
print(stats.norm.cdf(-0.7715))
print(0.9174 - 0.2202)
P(Z<=1.388) - P(Z<= (-0.7715)) = 0.9174 - 0.2202 = 0.6972
EX-02)n = 15 , p = 0.4 , 연속성 수정한 정규근사에 의한 P(7<=X<=9)의 근사확률
P(7 - 0.5 <= X <= 9 +0.5) = P( Z<= (6.5 - 6) / 루트(15*0.4*0.6) ) - P( Z<=(9.5 - 6) / 루트(15*0.4*0.6) )
==>P(Z<=0.2635) - P(Z<=1.844) = 0.9674 - 0.6039 = 0.3635
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 연속확률변수' 카테고리의 다른 글
[PYTHON]_코테에서도 쓰일_조합_계산_파스칼의 삼각형_시간복잡도(이항정리, 이항계수) 사용하기!!
1. itertools.combination 사용하기
https://knowallworld.tistory.com/146
[Python] 순열, 조합, 중복순열, 중복조합(itertools이용한 백트래킹)
https://knowallworld.tistory.com/228 Permutations()★순열,조합,중복순열,중복조합★기초통계학-[Chapter04 - 경우의 수] https://knowallworld.tistory.com/146 [Python] 순열, 조합, 중복순열, 중복조합(itertools이용한 백트
knowallworld.tistory.com
==> 참고하기
EX) 50C3
print(len(list(itertools.combinations(np.arange(50) , 3))))
2. 파스칼의 삼각형


파스칼의 삼각형:
import sys
N, M = list(map(int, sys.stdin.readline().rstrip().split(' ')))
# DP 활용한 파스칼삼각형 풀기
# nCk = (n-1)C(k-1) + (n-1)Ck
# 파스칼 삼각형 선언
pascal = [0]
for dp in range(2, N+2):
pascal.append([0]*dp)
print(pascal)
# # pascal[i] = [1, ?, ?, ..., ?, 1]에서 i는 nCk에서 n, 리스트의 인덱스는 k를 의미
pascal[1] = [1, 1]
for dp in range(2, N):
pascal[dp][0] = 1
for idx in range(1, dp):
pascal[dp][idx] = (pascal[dp-1][idx-1] + pascal[dp-1][idx]) % 10007
pascal[dp][-1] = 1
print(pascal)
if M == 0 or M == N:
print(1)
else:
print((pascal[N-1][M-1] + pascal[N-1][M]) % 10007)
#%%5C2 = 10


3. 시간복잡도(O(n) )
result = 1
N = 5
K = 3
for i in range(K):
result *= N
N -= 1
print('result : {}'.format(result))
print('N : {}'.format(N))
divisor = 1
for i in range(2, K+1):
divisor *= i
print('divisor : {}'.format(divisor))
print( (result // divisor) % 10007)result : 60
N : 2
divisor : 6
10
==> % 10007 은 왜하는건가? ==> 그냥 해!
'Python(백준) > 백트래킹' 카테고리의 다른 글
| [Python] 순열, 조합, 중복순열, 중복조합(itertools이용한 백트래킹) (0) | 2022.10.25 |
|---|---|
| [백준 파이썬 15652번]N과M_4★백트래킹★visited리스트 앞부분 고려 (0) | 2022.10.25 |
| [백준 파이썬 15651번]N과M_3★백트래킹★visited리스트 앞부분 고려 (0) | 2022.10.25 |
| [백준 파이썬 15650번]N과M_2★백트래킹★매개변수 고려 (0) | 2022.10.25 |
| [백준 파이썬 15649번]N과M★백트래킹★ (0) | 2022.10.25 |
★정규분포의 표준정규분포로의 변환★추측통계학-[Chapter06 - 연속확률분포-04]
1. 확률변수 X와 Y에 대한 분산

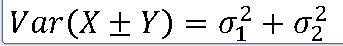
2. 서로 독립인 확률변수 X와 Y가 정규분포 X ~N(뮤_1 , 분산) , Y~ N(뮤_2 , 분산) 따르는 경우의 추측통계학



EX-01) X는 N(1995 , 144) Y는 N(1755 , 100)
1> X-Y의 확률분포
X-Y ~ N(1995 -1755 , 144 +100) --> N(240 , 244)
2> X와 Y의 가격 차이가 200이하일 확률
U = X-Y
U ~ N(200,244)
https://knowallworld.tistory.com/254
정규분포의 표준정규분포로의 변환★기초통계학-[Chapter06 - 연속확률분포-03]
1. 정규분포와 표준정규분포의 관계 =========================== ==> P(z_a =2.5 , facecolor = 'skyblue') # x값 , y값 , 0 , x= 2.5) = P(Z 박테리아의 수가 75마리 이상 103마리 이하일 확률 P(75
knowallworld.tistory.com
P(U <= 200) = P(Z< (200 - 240) / 루트(244) ) = P(Z<= -2.56) = 0.0052
area = stats.norm.cdf(-2.56) #area = 0.025
area
2> X와 Y의 가격 차이가 220이상 260 사이일 확률
print(20 / math.sqrt(244))
print(-20 / math.sqrt(244))z_a = 1.28
z_b = -1.28
area = stats.norm.cdf(1.28) - stats.norm.cdf(-1.28) #area = 0.025
area
P(220<= U <= 260) =P(Z< (260 - 240) / 루트(244) ) - P(Z< (220 - 240) / 루트(244) ) = P(Z<1.28) - P(Z<-1.28) = 0.7994
EX-02) X는 N(24.6 , 16.4**2) Y는 N(12.2 , 6.9**2)
1>X-Y의 확률분포
X-Y ~ N(12.4 , 16.4**2 + 6.9**2) ==> N(12.4 , 316.57)
2>X와 Y의 차이가 10과 20사이일 확률
X-Y = U
P(10<=U<=20) = P( Z<= (20 - 12.4) / 루트(316.57) ) - P( Z<= (10 - 12.4) / 루트(316.57) )= P(Z<=0.42714) - P(Z<= -0.13488) = 0.219
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 연속확률변수' 카테고리의 다른 글
정규분포의 표준정규분포로의 변환★기초통계학-[Chapter06 - 연속확률분포-03]
1. 정규분포와 표준정규분포의 관계

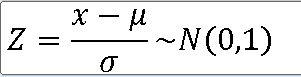
===========================
==> P(z_a <= Z <= z_b)
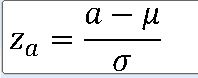

EX-01) N(50, 10**2) ==> P(X<=63.1)
z_0 = (63.1 - 50) / 10 = 1.31
==> P(Z<= 1.31)
EX-02) 평균 90마리, 표준편차 10마리인 정규분포
1> 박테리아의 수가 80마리 이하일 확률
P(X<= 80)
N(90 , 10**2)
z_0 = (80 -90) / 10 = -1
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
#ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x>=0 , facecolor = 'pink')
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x<=-1 , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
#ax.text(0.3, .10, f'P(Z>=0) \n{0.5}',fontsize=20)
area = stats.norm.cdf(-1)
ax.text(-3 , .135, f'P(Z<=-1 : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(-1.2, .125), xytext=(-2.2 , .125) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -1.03, ymin= 0 , ymax= stats.norm.pdf(-1.03, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))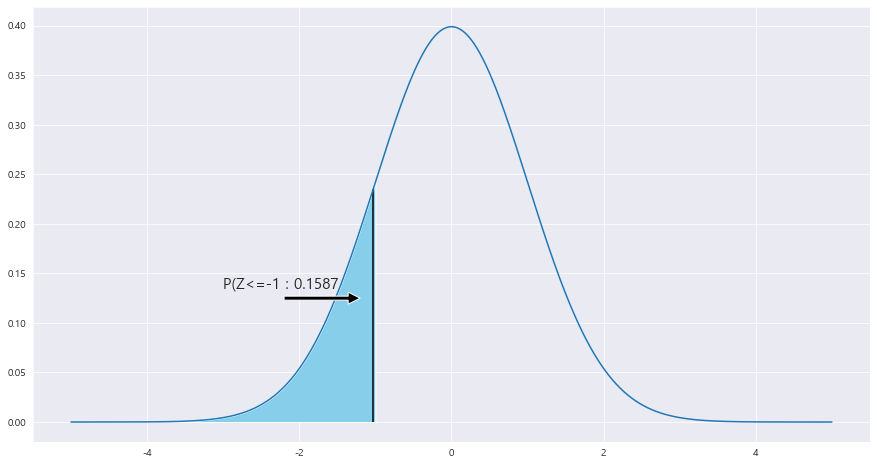
P(Z<= -1) = 0.1587
2> 박테리아의 수가 115마리 이상일 확률
P(X>=115) ~ N(90 , 10**2)
z_1 = 115 - 90 / 10 = 2.5
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x>=2.5 , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = stats.norm.cdf(-2.5)
ax.text(2.8 , .056, f'P(Z>=2.5 : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.7, .0025), xytext=(2.7 , .05) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= 2.5, ymin= 0 , ymax= stats.norm.pdf(2.5, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
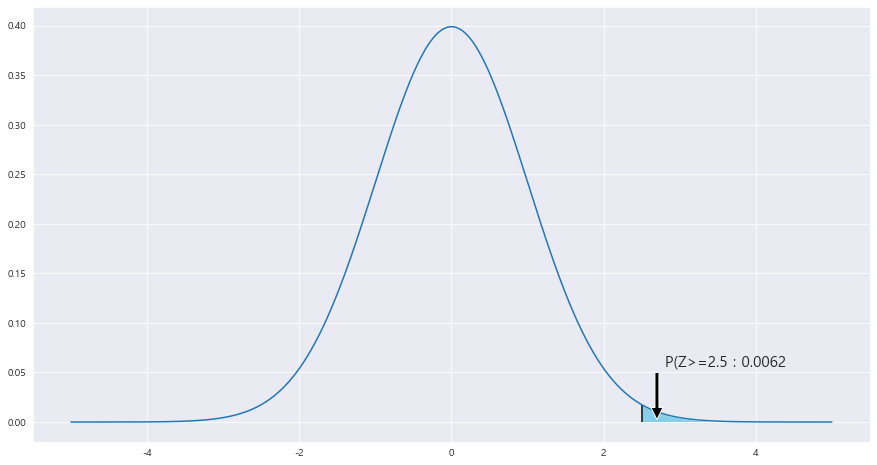
P(Z>= 2.5) = P(Z<= -2.5) = 0.0062
3> 박테리아의 수가 75마리 이상 103마리 이하일 확률
P(75<=X<=103)
z_a = (75 - 90) / 10 = -1.5
z_b = 103 -90 / 10 = 1.3
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=1.3) & (x>=-1.5) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = stats.norm.cdf(1.3) - stats.norm.cdf(-1.5)
ax.text(1.71 , .17, f'P(-1.5<=Z<=1.3) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= 1.3, ymin= 0 , ymax= stats.norm.pdf(1.3, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -1.5, ymin= 0 , ymax= stats.norm.pdf(-1.5, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
P(-1.5<=Z <= 1.3) = P(Z<=1.3) - P(Z<=-1.5) = 0.8364
EX-03) 평균 124 mmHg , 표준편차 8 mmHg
1> 120 mmHg 이하일 확률
P(X<=120) ~ N(124 , 8**2)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
#ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x>=0 , facecolor = 'pink')
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x<=-0.5 , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
#ax.text(0.3, .10, f'P(Z>=0) \n{0.5}',fontsize=20)
area = stats.norm.cdf(-0.5)
ax.text(-3 , .135, f'P(Z<=-0.5 : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(-1.2, .125), xytext=(-2.2 , .125) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -0.5, ymin= 0 , ymax= stats.norm.pdf(-0.5, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))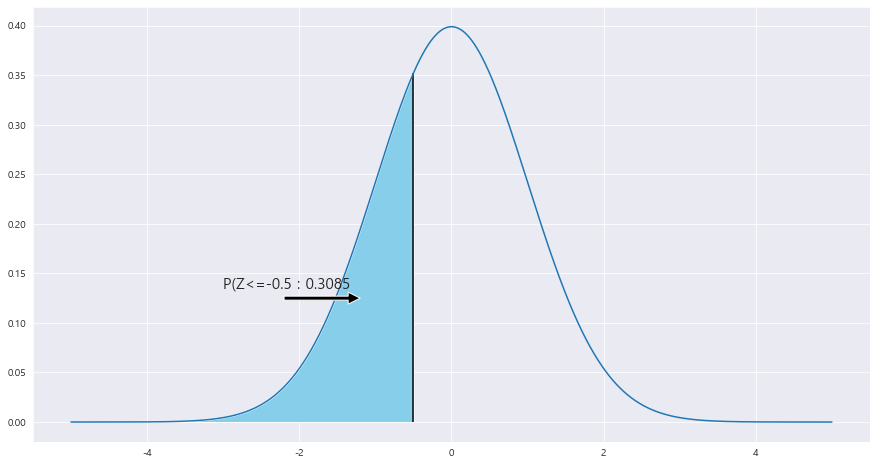
P(Z<= -4/8) = P(Z<= -0.5) = 0.3085
2> 142 mmHg 이상일 확률
P(X=>142) ~ N(124 , 8**2)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x>=2.25 , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = stats.norm.cdf(-2.25)
ax.text(2.8 , .056, f'P(Z>=2.5 : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.7, .0025), xytext=(2.7 , .05) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= 2.25, ymin= 0 , ymax= stats.norm.pdf(2.25, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))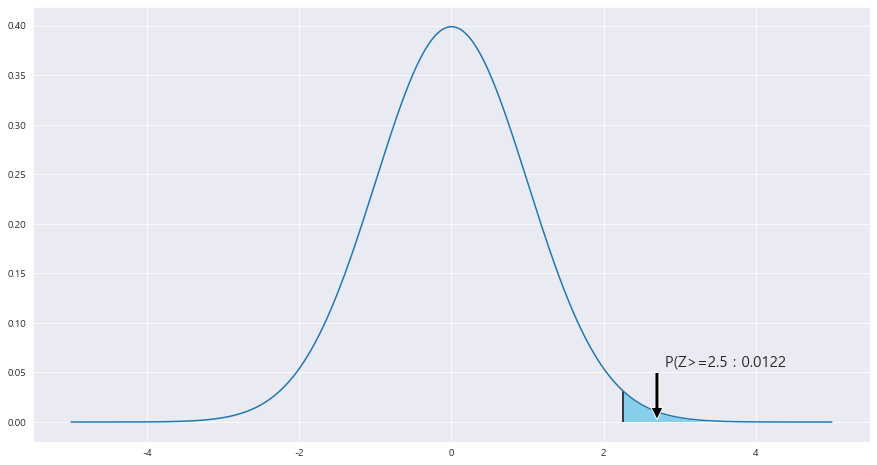
P(Z>= 18/8) = P(Z>= 2.25) = P(Z<= -2.25) = 0.0122
3> 115 mmHg 이상, 136 mmHg 이하일 확률
P(115 <= X <= 136) ~ N(124 , 8**2)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=1.5) & (x>=-(9/8)) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = stats.norm.cdf(1.5) - stats.norm.cdf(-(9/8))
ax.text(1.71 , .17, f'P(-(9/8)<=Z<=1.5) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .17), xytext=(1.7 , .17) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= 1.5, ymin= 0 , ymax= stats.norm.pdf(1.5, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -(9/8), ymin= 0 , ymax= stats.norm.pdf(-(9/8), loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
P(115-124 / 8 <=Z <= 136 -124 / 8) = P(-9/8 <=Z <= 1.5) = P(Z<= 1.5) - P(Z<= -9/8) = 0.8029
EX-04> X ~ N(5, 2**2)

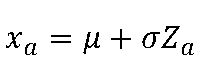
1> P(X> x_0) = 0.025를 만족하는 x_0
1 - P(X<= x_0) = 0.025
P(X<=x_0) = 0.975
area = stats.norm.ppf(0.975)
area==> ppf를 통한 z = 1.96값 얻을 수 있다.
https://knowallworld.tistory.com/252
sympy INTEGRAL,Symbol,pprint★scipy.stats.UDF_균등분포★stats.PDF_확률밀도함수★기초통계학-[Chapter06 - 연속
1. 연속확률변수(Continous Random Variable) ==> 확률변수가 취할 수 있는 모든 값, 상태공간이 어떤 구간으로 나타나는 확률변수 의미 ==> 확률변수 X가 취할 수 있는 모든 값이 유한구간 [a,b] or [(0, 무한
knowallworld.tistory.com
==> ppf , pdf , sf, cdf 참고
x_0 = 5 + 2* 1.96 = 8.92
2> P(X< x_0) = 0.9265를 만족하는 x_0
area = stats.norm.ppf(0.9265)
areaz = 1.45
x_0 = 5 + 2 * 1.45 = 7.9
3> P(5-x_0 < X < 5+ x_0) = 0.8262를 만족하는 x_0
z_a = (5-x_0 - 5) / 2 = - (x_0) / 2
z_b = (5+x_0 - 5) / 2 =(x_0) / 2
P(- (x_0) / 2 < Z < (x_0) / 2) = 2 * P(0 < Z<(x_0) / 2 ) = 0.8262
P(0< Z< (x_0 / 2 ) = 0.4131
area = stats.norm.ppf(0.5 + 0.4131)
areax_0 / 2 = 1.36
x_0 = 2.72
EX-05> X ~ N(150, 5**2)
1> P(X>x_0) = 0.0055 만족하는 x_0
area = stats.norm.ppf(1- 0.0055)
areaP(X<=x_0) = 1 - 0.0055
z_0 = 2.5426
x_0 = 150 + 5*(2.5426) = 162.713
2> P(X<x_0) = 0.9878 만족하는 x_0
z_0 = 2.25
x_0 = 150 + 5*(2.25) = 161.25
3> P(150-x_0 < X<150 + x_0) = 0.9010 만족하는 x_0
z_a = (150-x_0 -150 ) / 5 = -x_0 / 5
z_b = (150+x_0 - 150 ) / 5 = x_0 / 5
P(-x_0/5 < Z < x_0/5) = 2 * P(0< Z < x_0 /5) = 0.9010
P(0< Z < x_0 /5) = 0.9010 / 2
area = stats.norm.ppf(0.5 + 0.9010 /2 )
areax_0 / 5 = 1.6497
x_0 = 8.2485
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 연속확률변수' 카테고리의 다른 글
stats.norm.cdf()★표준정규분포 넓이 구하기!!★ax.lineplot★정규분포(Normal Distribution)★기초통계학-[Chapter06 - 연속확률분포-02]
1. 정규분포(Normal Distribution)
==> 자료 집단에 대한 도수히스토그램은 자료의 수가 많을 수록 종 모양에 가까운 형태로 나타난다.
==> 종 모양의 확률분포를 정규분포라고 한다.
1>정규분포의 성질
평균 myu(뮤)와 분산에 대하여 확률밀도함수를 가지는 연속확률분포
https://knowallworld.tistory.com/216
★distplot , histplot , twinx(), ticker , axvline()★정규분포 그래프★기초통계학-[Chapter03 - 05]
1. A 데이터프레임 생성 A='30.74 28.44 30.20 32.67 33.29 31.06 30.08 30.62 27.31 27.88 ' \ '26.03 29.93 31.63 28.13 30.62 27.80 28.69 28.14 31.62 30.61 ' \ '27.95 31.62 29.37 30.61 31.80 29.32 29.92 31.97 30.39 29.14 ' \ '30.14 31.54 31.03 28.52 28.
knowallworld.tistory.com


==> 정규분포는 중심위치에서 꼭짓점이 하나인 종 모양이다. 평균, 중위수, 최빈값이 분포의 중심위치로 동일하다.
==> 평균은 서로 다르지만, 표준편차가 동일한 경우 중심 위치는 다르지만 모양은 동일하게 나타난다.
==> 평균은 동일하지만 , 표준편차가 다른 경우 자료가 평균에 밀집하고 클수록 자료가 퍼지는 모양을 갖는다.
x = np.arange(-10,10 ,.001)
fig = plt.figure(figsize= (15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
sns.lineplot(x , stats.norm.pdf(x, loc=8 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale= 2)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =5)) #정의역 범위 , 평균 = 0 , 표준편차 =5 인 정규분포 플롯
ax.axvline(x= 0, ymin=0 , ymax=1 , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(0, .41, f'평균 : {round(0,2)}',fontsize=13)
plt.legend(['N(0,1)' , 'N(2,1)' , 'N(0,2)' , 'N(0,5)'] , fontsize = 15)
2. 표준정규분포(Standard Normal Distribution)
==> 평균이 0이고 , 분산이 1 인 정규분포


x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x>=0 , facecolor = 'red')
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x<=0 , facecolor = 'blue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
ax.text(0.3, .10, f'P(Z>=0) \n{0.5}',fontsize=20)
ax.text(-1, .10, f'P(Z<0) \n{0.5}',fontsize=20)
==> 확률 P(Z<=0) = P(Z>=0)
꼬리확률(Tail Probability)
==> P(Z<=a) = P(Z>=a)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (-3<x) & (x<3) , facecolor = 'skyblue') #where 절 and는 &활용
ax.vlines(x= 3, ymin= 0 , ymax= stats.norm.pdf(3, loc=0 , scale =1) + 0.1 , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -3, ymin= 0 , ymax= stats.norm.pdf(-3, loc=0 , scale =1) + 0.1 , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
plt.annotate('' , xy=(-3, .10), xytext=(0 , .10) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(3, .10), xytext=(0 , .10) , arrowprops = dict(facecolor = 'black'))
ax.text(-1, .12, f'P(-3<=Z<=3) : {0.997}',fontsize=15)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (-2<x) & (x<2) , facecolor = 'skyblue') #where 절 and는 &활용
ax.vlines(x= 2, ymin= 0 , ymax= stats.norm.pdf(2, loc=0 , scale =1) + 0.2 , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -2, ymin= 0 , ymax= stats.norm.pdf(-2, loc=0 , scale =1) + 0.2 , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
plt.annotate('' , xy=(-2, .20), xytext=(0 , .20) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(2, .20), xytext=(0 , .20) , arrowprops = dict(facecolor = 'black'))
ax.text(-1, .22, f'P(-2<=Z<=2) : {0.954}',fontsize=15)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (-1<x) & (x<1) , facecolor = 'pink') #where 절 and는 &활용
ax.vlines(x= 1, ymin= 0 , ymax= stats.norm.pdf(1, loc=0 , scale =1) + 0.3 , color = 'blue' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -1, ymin= 0 , ymax= stats.norm.pdf(-1, loc=0 , scale =1) + 0.3 , color = 'blue' , linestyle ='solid' , label ='{}'.format(2))
plt.annotate('' , xy=(-1, .50), xytext=(0 , .50) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(1, .50), xytext=(0 , .50) , arrowprops = dict(facecolor = 'black'))
ax.text(-1, .52, f'P(-1<=Z<=1) : {0.683}',fontsize=15)

==> 경험적 규칙에 따라
==> P(|Z| <=1) = 0.683 , P(|Z| <=2) = 0.954 , P(|Z| <=1) = 0.997
EX-01) P(Z<= 1.96)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
#ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x>=0 , facecolor = 'pink')
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x<=1.96 , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
#ax.text(0.3, .10, f'P(Z>=0) \n{0.5}',fontsize=20)
area = stats.norm(0,1).cdf(1.96) # area 계산!!
ax.text(-1, .10, f'P(Z<=1.96) \n{area}',fontsize=20)
ax.vlines(x= 1.96, ymin= 0 , ymax= stats.norm.pdf(1.96, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))

EX-02) P(Z>= 2.03)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
#ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x>=0 , facecolor = 'pink')
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x>=2.03 , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
#ax.text(0.3, .10, f'P(Z>=0) \n{0.5}',fontsize=20)
area = 1- stats.norm.cdf(2.03) #넓이 구하기!!!!!
ax.text(2.5 , .05, f'P(Z>=2.03) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(2.2, .02), xytext=(2.5 , .04) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= 2.03, ymin= 0 , ymax= stats.norm.pdf(2.03, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
EX-03) P(Z<= -0.57)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
#ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x>=0 , facecolor = 'pink')
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x<=-0.57 , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
#ax.text(0.3, .10, f'P(Z>=0) \n{0.5}',fontsize=20)
area = stats.norm.cdf(-0.57)
ax.text(-3 , .11, f'P(Z<=-0.57) : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(-1.7, .02), xytext=(-2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= -0.57, ymin= 0 , ymax= stats.norm.pdf(-0.57, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))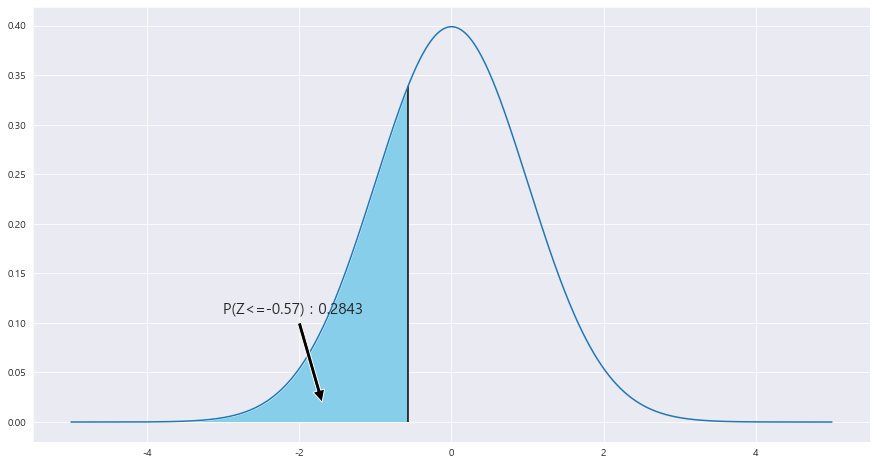
EX-04) P(-1.75<=Z<= 2.12)
= P(Z<=2.12) - P(Z<=-1.75)
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
#ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x>=0 , facecolor = 'pink')
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=2.12) & (x>=-1.75) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
#ax.text(0.3, .10, f'P(Z>=0) \n{0.5}',fontsize=20)
area = stats.norm.cdf(2.12) - stats.norm.cdf(-1.75)
ax.text(-3 , .17, f'P(-1.75<=Z<=2.12 : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .15), xytext=(-2 , .15) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= 2.12, ymin= 0 , ymax= stats.norm.pdf(-2.12, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -1.75, ymin= 0 , ymax= stats.norm.pdf(-1.75, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
EX-05) P(-1.03<=Z<= 1.03)
= P(0<=Z<=1.03) * 2 = ( P(Z<=1.03) - P(Z<=0) ) * 2 =
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =2 인 정규분포 플롯
#ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = x>=0 , facecolor = 'pink')
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=1.03) & (x>=-1.03) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
#ax.text(0.3, .10, f'P(Z>=0) \n{0.5}',fontsize=20)
area = ( stats.norm.cdf(1.03) - stats.norm.cdf(0) ) * 2
ax.text(-3 , .27, f'P(-1.03<=Z<=1.03 : {round(area,4)}',fontsize=15)
plt.annotate('' , xy=(0, .25), xytext=(-2 , .25) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= 1.03, ymin= 0 , ymax= stats.norm.pdf(-1.03, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -1.03, ymin= 0 , ymax= stats.norm.pdf(-1.03, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 연속확률변수' 카테고리의 다른 글
sympy INTEGRAL,Symbol,pprint★scipy.stats.UDF_균등분포★stats.PDF_확률밀도함수★기초통계학-[Chapter06 - 연속확률분포-01]
1. 연속확률변수(Continous Random Variable)
==> 확률변수가 취할 수 있는 모든 값, 상태공간이 어떤 구간으로 나타나는 확률변수 의미
==> 확률변수 X가 취할 수 있는 모든 값이 유한구간 [a,b] or [(0, 무한대)] 일 경우 확률변수 X를 연속확률변수라 한다.
EX-01)
1>X는 오차가 2mL 이고 용량이 245mL로 표시된 음료수의 양
==> 연속확률변수
2>X는 시험시간이 1시간인 시험에서 각각의 학생들이 답안지를 제출한 시간
==> 연속확률변수
3> X는 교체된 형광등의 수명
==> 연속확률변수
4> X는 카드 외판원이 3장의 카드를 판매할 때까지 만난 고객의 수
==> 이산확률변수
5> 교환대에 걸려온 전화 횟수
==> 이산확률변수
6> X는 교환대에 걸려온 전화 사이의 대기 시간
==> 연속확률변수
7> 강수량
==> 연속확률변수
2. 확률밀도함수(Probability Density Function , PDF)
==> 모든 실수 x에 대하여 f(x) >= 0
==> 모든 실수 구간과 함수 f(x)로 둘러싸인 부분의 넓이는 1이다.

==> 자료 값의 갯수가 늘어날 수록 계급간격이 조밀해지고, 상대도수히스토그램은 곡선에 가까워진다.
EX-01) 중심부에 있는 가장 작은 원의 반지름 : 5mm , 2번째 작은 원의 반지름 1cm , 1칸당 1cm씩 커진다.
P(X<=x) = (반지름의 길이가 x인 원의 넓이) / (전체 원의 넓이)
1> 중심부에 있는 가장 작은 원에 맞힐 확률:
r = 0.5cm
s = 0.25ㅠ cm**2
S = 100ㅠ cm**2
P(X=0.5) = 0.25 / 100 = 1/400 = 0.0025
2> 반지름의 길이가 a보다 작은 원에 맞힐 확률:
P(X<=a) = a**2 / 100
3> 반지름의 길이가 3cm와 4cm 원안에 맞힐 확률:
P(X=3) + P(X=4) =P(X<=4) - P(X<=2) = 16/100 - 4/100 = 12/100 = 0.12 (WHY??!)
P(X=3) + P(X=4) =P(X<=4) - P(X<=3) = 16/100 - 9/100 = 12/100 = 0.07
4> 반지름의 길이가 4cm 원 밖에 맞힐 확률:
P(X>=4) = 1 - P(X<=4) = 1 - 16/100 = 84/100 = 0.84
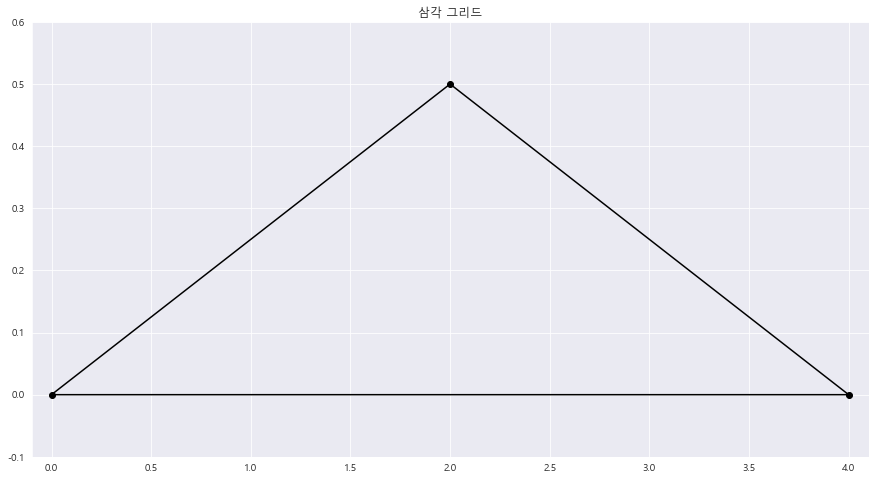
EX-02) 연속확률변수 X의 확률밀도함수 f(x) 가 삼각형 모양
import matplotlib.tri as mtri
fig = plt.figure(figsize=(15,8))
x = np.array([0,2,4]) #삼각형의 x좌표
y = np.array([0,0.5 , 0]) #삼각형의 y좌표
triangles = [[0,1,2]] #삼각형의 점 개수
triang = mtri.Triangulation(x,y , triangles)
plt.title("삼각 그리드")
plt.triplot(triang , 'ko-')
plt.xlim(-0.1 , 4.1)
plt.ylim(-0.1 , 0.6)
plt.show()==> Matplotlib.tri 활용하여 삼각형 그리드 시각화
1> 상수 k를 구하라.
k = 0.5
y = (1/4)x ____ 0<=x<2
y = (-1/4)x + (1) _____ 2<=x<=4
2> P(X<=1) = 1/8
3> P(1<=X<=2) = 1/2 - 1/8 = 3/8
4> P(X>=2.5) = (- (25/40) + (40/40) ) * (3/2) * (1/2) = 15/40 * (3/2) *(1/2) = 3/8 * 3/4 = 9/32 = 0.28125
==> 추후 시각화 자료 첨부할 예정
3. 균등분포(Uniform Distribution , PDF)
==> 구간 a<=x <= b
==> f(x) = 1 / (b-a)
==> X ~ U(a,b)
==> P(X<=c) = (c-a) / (b-a)
※균등분포 그래프 그리기!!!!!!
min , max = 270, 300
# x_2 = linspace(min-1 , max+1 , 100)
x_2 = np.arange(min-30 , max+30 , 1)
print(x)
print(x_2)[240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257
258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275
276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293
294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311
312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329]
y = uniform.pdf( x = x_2 , loc = min , scale = max-min)
# f(x, loc, scale) = {1/scale-loc for loc <= x <= scale
# {0 otherwise}
print(y)[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0.033 0.033 0.033 0.033 0.033 0.033
0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
0.033 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. ]
fig = plt.figure(figsize=(12, 8))
ax = sns.lineplot(x = x_2 , y= y) #왜 uniform이 안되는거죵
ax.set_title('균등분포(Uniform Distribution)')
ax.set_xlabel('X' , fontsize= 15)
ax.set_ylabel('Y' , fontsize= 15 , rotation = 0 , labelpad = 12)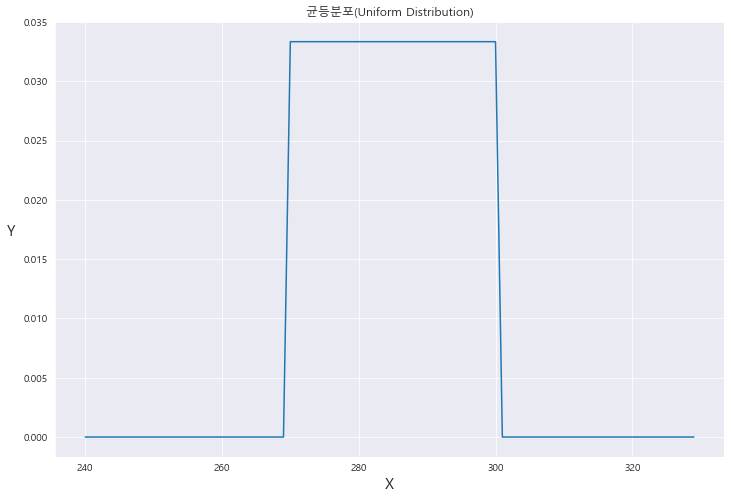
★★★★★https://github.com/scipy/scipy/blob/main/scipy/stats/_continuous_distns.py
GitHub - scipy/scipy: SciPy library main repository
SciPy library main repository. Contribute to scipy/scipy development by creating an account on GitHub.
github.com
==> Scipy 링크 참조!!!!
1> P(X<= x) ==> [1,5] 구간에서 P(X<=3)
stats.uniform.cdf(loc=1 , scale= 4 , x=3)2> P(X> x) ==> [1,5] 구간에서 P(X>2)
stats.uniform.sf(loc=1 , scale = 4 , x =2)3> f(x) ==> [1,5] 구간에서 확률밀도함수
for i in range(1,6):
print(stats.uniform.pdf(loc=i , scale = 4 , x =5))f(1) = P(X=1) = 0.2
4> f(x) ==> [1,5] 구간에서 넓이 값(백분위수)
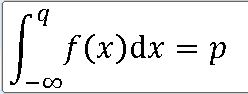
5> number 개수만큼 난수 발생
print(stats.uniform.rvs(loc = 1, scale = 5.0 , size = 10))[5.84 2.235 4.449 2.765 5.692 1.512 4.586 4.765 2.102 3.478]
==> scale은 6미만?!
EX-01) X ~ U(1, 5) ==> Y축 1/4 , X축 (1,5)
1> X의 확률밀도함수
f(x) = 1/4 ( 1<=x <= 5) , 0 ( x<1 , x>5)
for i in range(1,6):
print(stats.uniform.pdf(loc=i , scale = 4 , x =6))==>0.0 ,0.25 , 0.25 ,0.25 , 0.25
==> scale 4로 설정!!! ==> 갯수의미!
2> P(X<=3)
print(stats.uniform.cdf(loc=1 , scale= 4 , x=3))==> scale 4로 설정!!! ==> 갯수의미!
=> 2 * 1/4 = 1/2
3> P(2<=X<=3.5)
stats.uniform.cdf(loc=1 , scale = 4 , x=3.5) - stats.uniform.cdf(loc=1 , scale = 4 , x =2)==> scale 4로 설정!!! ==> 갯수의미!
==> 1.5 * 1/4 = 15/10 * 1/4 = 3/8 = 0.375
EX-02) X ~ U(0,4)
1> X의 확률밀도함수
for i in range(0,5):
print(stats.uniform.pdf(loc=i , scale = 4 , x=5))==> 0.0 , 0.25 , 0.25 , 0.25, 0.25
f(x) = 1/4 , 0<=x<=4 , x<0 or x>4
2> P(X<=3)
print(stats.uniform.cdf(loc=0 , scale = 4 , x=3))3* 1/4 = 3/4 = 0.75
4. 연속확률변수의 평균과 분산
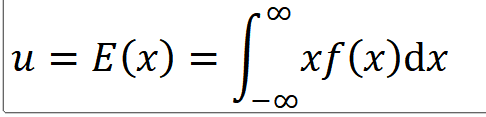

EX-01) 확률밀도함수가 0<=x<=1 에서 f(x) = 2x
1> X의 평균
from sympy import Integral, Symbol , pprint
x = Symbol('x')
f = 2 * x**2
pprint(Integral(f, x).doit()) #이쁘게 출력
print(Integral(f, (x, 0, 1)).doit()) #적분변수 , 아래끝 , 위끝 3
2⋅x
──── ==> 적분한 값
3
E(X) = 2/3
2> X의 분산
f = f *x
print(Integral(f, (x, 0, 1)).doit() - a**2) #적분변수 , 아래끝 , 위끝1/18
3> P(0<=X<=0.5)
f = 2*x
print(Integral(f, (x, 0, 0.5)).doit())==> 0.25
EX-02) 연속확률벼수 X의 확률밀도함수가 -1<=x<=1 에서 f(x) = (x+1) / 2
x = Symbol('x')
f_x = (x+1) /2
f_x_m = f_x * x
print(f_x_m)
mean_1 = Integral(f_x_m, (x,-1 , 1)).doit()
print("평균 : {}".format(mean_1))
f_x_v = f_x_m * x
print(f_x_v)
vars_1 = Integral(f_x_v , (x,-1,1)).doit() - mean_1**2
print("분산 : {}".format(vars_1))
ratio = Integral(f_x , (x,0,0.5)).doit()
print("확률 0이상 0.5 이하는 {}이다.".format(ratio))X의 평균 : 1/3
X의 분산 : 2/9
P(0<= X <= 0.5) : 확률 0이상 0.5 이하는 0.3125이다.
EX-03) X ~ U(1,5)에 대하여 X의 평균과 분산을 구하라
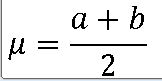

f = 1/ (5-1)
x = Symbol('x')
f_x_m = f*x
mean_x = Integral(f_x_m , (x,(1,5))).doit()
print("평균 : {}".format(mean_x))
f_x_v = f_x_m*x
var_x = Integral(f_x_v , (x,(1,5))).doit() - mean_x**2
print("분산 : {}".format(var_x))
mean_x = (1+5) / 2
var_x = (5-1)**2 / 12
print("평균 : {}".format(mean_x))
print("분산 : {}".format(var_x))평균 : 3.00000000000000
분산 : 1.33333333333333
평균 : 3.0
분산 : 1.3333333333333333
EX-04) X ~ U(0,4)에 대하여 X의 평균과 분산을 구하라
f = 1/ (4-0)
x = Symbol('x')
f_x_m = f*x
mean_x = Integral(f_x_m , (x,(0,4))).doit()
print("평균 : {}".format(mean_x))
f_x_v = f_x_m*x
var_x = Integral(f_x_v , (x,(0,4))).doit() - mean_x**2
print("분산 : {}".format(var_x))
mean_x = (0+4) / 2
var_x = (4-0)**2 / 12
print("평균 : {}".format(mean_x))
print("분산 : {}".format(var_x))평균 : 2.00000000000000
분산 : 1.33333333333333
평균 : 2.0
분산 : 1.3333333333333333
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용