전체 글
-
변동계수★기초통계학-[Chapter03 - 08]2022.12.07
-
경험적규칙★체비쇼프 정리★기초통계학-[Chapter03 - 06]2022.12.06
-
WINDOWS 11에서 MATH INPUT PANEL 을 사용해보자!2022.12.05
-
np.median★절사평균, 중위수★기초통계학-[Chapter03 - 03]2022.12.02
변동계수★기초통계학-[Chapter03 - 08]
1. 변동계수(Coefficient of Variation)
표준편차는 평균을 중심으로 자료 집단 안의 자료 값들의 놓인 위치에 대한 산포의 척도
==> 측정 단위가 동일하지만 평균이 큰 차이를 보이는 두 자료 집단 또는 측정 단위가 서로 다른 두 자료 집단에 대한 산포의 척도로 절대적 수치인 표준편차를 사용하기에는 부적절
==> ex) 신생아 몸무게 vs 산모 몸무게
==>단위에 관계없이 양수인 값을 가지며 평균으로 부터 상대적으로 흩어진 정도를 나타내는 척도


==> 변동계수가 클수록 자료의 분포는 상대적으로 폭이 넓다
EX-01)
A = pd.DataFrame({'가구원 수(명)' : [4.06 , 1.02] , '외식비(원)' : [175420 , 33250]})
A.index = ['|x' , 's']
A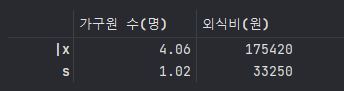
a = pd.DataFrame([(A.iloc[1,0]/A.iloc[0,0])*100, (A.iloc[1,1]/A.iloc[0,1])*100]) #변동계수 구하기
a = a.transpose()
a = a.rename(columns = {0 : A.columns[0] , 1 : A.columns[1]})
a.index= ['변동계수']
A = pd.concat([A ,a])
A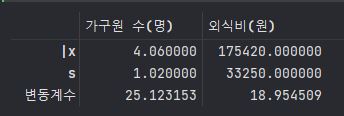
==> 표본의 변동계수 식으로 구한 결과값 :
가구원 CV : 25.123
외식비 CV: 18.9545
==> 가구원의 흩어진 정도가 1.3배 정도 크다
==> 표준편차
가구원 표준편차 : 2.1496
외식비 표준편차 : 100529.371
==> 이처럼 단위가 다른 자료에 대한 산포도를 파악할 수 있다.
EX-02)
company = ['삼성전자' , 'SK텔레콤' , 'LG전자' , 'GS칼텍스' , '롯데쇼핑' , '현대자동차' , '현대케미칼' , '대한항공' , '포스코' , '현대중공업']
SALARY = [10200,10500,6900,9107,3353,9400,6779,6400,7900,7232]
YEAR = [9.3,12.4,8.5,14.6,5.7,16.8,12.2,13.8,18.5,18.0]
B = pd.DataFrame({'회사명' : company , '평균 연봉(만 원)' : SALARY , '근속 연수(년)' : YEAR})
B = B.set_index('회사명')
BSALARY_CV = np.std(B.iloc[:,0] , ddof =1) / np.mean(B.iloc[:,0])
YEAR_CV = np.std(B.iloc[:,1] , ddof =1) / np.mean(B.iloc[:,1])
b = pd.DataFrame(['변동계수(CV)' , SALARY_CV , YEAR_CV])
b = b.transpose().set_index(0)
b = b.rename(columns = {1 : B.columns[0] , 2 : B.columns[1]})
B = pd.concat([B,b])
B==> NUMPY 라이브러리 적극 활용 , ddof= 1 ==> 표본표준편차 설정

==> 근속연수에 대한 산포도가 평균 연봉에 대한 산포도보다 높음을 알 수 있다.
https://knowallworld.tistory.com/214
★DDOF = 1★모/표본분산 , 모/표본표준편차★평균편차★기초통계학-[Chapter03 - 04]
산포의 척도 ==> 평균깊이가 1.2M인 강을 키가 1.7M인 사람이 걸어서 무사히 건널 수 있는지에 대해 생각 ==> 강의 평균 깊이가 1.2M 라는 뜻은 1.2M보다 작은 부분도 있지만 1.2M보다 깊은 곳도 있을 수
knowallworld.tistory.com
ddof =1 을 해야하는 이유!!!!


출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 평균,표준편차,분산' 카테고리의 다른 글
| Lmport★np.cov()★공분산★상관관계(Correlation)★상관계수(Coefficient)★기초통계학-[Chapter03 - 10] (0) | 2022.12.07 |
|---|---|
| annotate★IQR★boxplot★z-점수와 분위수★기초통계학-[Chapter03 - 09] (0) | 2022.12.07 |
| insert() , index★그룹화 자료의 분산과 표준편차★기초통계학-[Chapter03 - 07] (0) | 2022.12.07 |
| 경험적규칙★체비쇼프 정리★기초통계학-[Chapter03 - 06] (0) | 2022.12.06 |
| ★distplot , histplot , twinx(), ticker , axvline()★정규분포 그래프★기초통계학-[Chapter03 - 05] (0) | 2022.12.06 |
insert() , index★그룹화 자료의 분산과 표준편차★기초통계학-[Chapter03 - 07]
1. 그룹화 자료의 분산과 표준편차
A ='29 30 49 21 39 38 15 39 48 41 50 38 33 40 51 29 31 42 29 69 37 20 49 40 10 49 49 49 35 45 22 45 20 45 30 41 40 38 10 31 47 19 31 21 41 46 28 29 18 28'
A = list(map(int, A.split(' ')))
AA = [29, 30, 49, 21, ············]
B = pd.DataFrame({'계급간격' : interval ,'도수(f_i)' : hist , '계급값(x_i)' : Steps} )
B= B.set_index('계급간격')
BB['f_i_x_i'] = B['도수(f_i)'] * B['계급값(x_i)']
B['x_i - |x'] = B['도수(f_i)'] - round(float(A.mean()),2)
B['(x_i - |x)**2'] = B['x_i - |x']**2
B['(x_i - |x)**2 * f_i'] =B['(x_i - |x)**2'] *B['도수(f_i)']
Ba = pd.DataFrame(B[:].sum(axis=0))
# a.transpose()
a = a.transpose()
a[['계급값(x_i)', 'x_i - |x' , '(x_i - |x)**2', 'f_i_x_i'] ] = '-'
aa.index = ['합계']
a==> INDEX 값 재설정
B = pd.concat([B , a])
B==> 밑에 집어넣기
C = pd.DataFrame({'계급간격' : ['0.5~4.5' , '4.5~8.5' , '8.5~12.5' , '12.5~16.5' , '16.5~20.5' , '20.5~24.5', '24.5~28.5', '28.5~32.5'] ,'도수(f_i)' : [25,55,60,90,115,85,50,20] , '계급값(x_i)' : [2.5,6.5,10.5,14.5,18.5,22.5,26.5,30.5]} )
C= C.set_index('계급간격')
CC['f_i_x_i'] = C['도수(f_i)'] * C['계급값(x_i)']
print(sum(C['f_i_x_i']))
C['x_i - |x'] = C['계급값(x_i)'] - (sum(C['f_i_x_i'])/sum(C['도수(f_i)']))
C['(x_i - |x)**2'] = (C['x_i - |x']**2)
C['(x_i - |x)**2 * f_i'] = (C['(x_i - |x)**2'] *C['도수(f_i)'])
C
var = (C.iloc[-1,-1] / C.iloc[-1,0])
std = math.sqrt(var)
print("분산 : {} 표본표준편차 : {}".format( var , std))분산 : 50.694399999999995 표본표준편차 : 7.119999999999999
표본평균 |X : sum(f_i_x_i) / sum(도수 합)
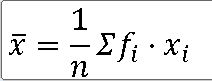
표본표준편차 s**2 : sum((x_i - |x)**2) / (sum(도수 합) -1)

f_i :.




https://knowallworld.tistory.com/214
★DDOF = 1★모/표본분산 , 모/표본표준편차★평균편차★기초통계학-[Chapter03 - 04]
산포의 척도 ==> 평균깊이가 1.2M인 강을 키가 1.7M인 사람이 걸어서 무사히 건널 수 있는지에 대해 생각 ==> 강의 평균 깊이가 1.2M 라는 뜻은 1.2M보다 작은 부분도 있지만 1.2M보다 깊은 곳도 있을 수
knowallworld.tistory.com
==>그룹화 자료의 분산은 표본 분산 구하는 공식에 도수를 곱한 값이다.
EX)
그룹화 자료형의 분산(s**2) = 60/(30-1) = 2.0689
표본분산(s) = 1.4383
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 평균,표준편차,분산' 카테고리의 다른 글
| annotate★IQR★boxplot★z-점수와 분위수★기초통계학-[Chapter03 - 09] (0) | 2022.12.07 |
|---|---|
| 변동계수★기초통계학-[Chapter03 - 08] (0) | 2022.12.07 |
| 경험적규칙★체비쇼프 정리★기초통계학-[Chapter03 - 06] (0) | 2022.12.06 |
| ★distplot , histplot , twinx(), ticker , axvline()★정규분포 그래프★기초통계학-[Chapter03 - 05] (0) | 2022.12.06 |
| ★DDOF = 1★모/표본분산 , 모/표본표준편차★평균편차★기초통계학-[Chapter03 - 04] (0) | 2022.12.02 |
경험적규칙★체비쇼프 정리★기초통계학-[Chapter03 - 06]

100개의 자료에서
구간 1 : [x-s , x+s] 안에 69개의 자료가 들어있다. ==> 3 + 5 + 6 + 4 + 9 + 1 + 6 + 4 + 7 + 8 + 4 + 9 + 3 = 69
구간 2: [x-2s , x+2s] ==> 69 + (1+1+2+4+1+5 + 2 + 4 +0 + 2 + 2 +2 +1) = 96
구간 3 : [x-3s , x+3s] ==> 96+ 2 +2 =100
===> 경험적 규칙(Empirical rule)에 의하여 자료의 68%가 [x-s , x+s] 안에있고,95%가 [x-2s , x+2s] , 99.7%가 [x-3s , x+3s]안에들어있다.
==> 이를 체비쇼프 정리라 한다.
==> k>1 에 대하여 전체 자료 중에서 적어도 100*(1- (1/k**2))%의 비율이 구간안에 존재한다.
EX-01 ) 자료의 수가 100인 자료 집단에 대하여 평균은 x = 30.138 , 표준편차 s= 1.991 이다.
구간 [x-2.5s , x+2.5s]안에 최소한 몇 개의 자료 값이 놓이는지 체비쇼프 정리를 이용하여 구하고, 실제 자료집단을 이용하여 그 개수를 구하기
print(100*(1- 1/(2.5)**2))
==> 84% ==> 적어도 84개의 자료 값이 이 구간 안에 놓인다.
==> 표본평균의 경우 30.138 표본표준편차 s= 1.991이므로, x-2.5s = 25.1605 || x+2.5s = 35.1155 이다.
==> 위의 그래프에서 보면 전체 자료를 크기순으로 나열하면 [x-2.5s , x+2.5s] = ( 25.1605 , 35.1155) 안에 100개의 자료가 있다.
EX-02 ) 자료의 수가 100인 자료 집단에 대하여 평균은 x = 30.138 , 표준편차 s= 1.991 이다.
구간 [x-1.5s , x+1.5s]안에 자료 값의 개수와 그 비율 구하기
print(100*(1- 1/(1.5)**2))==> 55.55% ==> 적어도 55.55%의 자료 값이 기 구간 안에 놓인다. ==> 적어도 55개
==> 표본평균의 경우 30.138 표본표준편차 s= 1.991이므로, x-1.5s = 27.1515 || x+1.5s = 33.1245 이다.
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 평균,표준편차,분산' 카테고리의 다른 글
| 변동계수★기초통계학-[Chapter03 - 08] (0) | 2022.12.07 |
|---|---|
| insert() , index★그룹화 자료의 분산과 표준편차★기초통계학-[Chapter03 - 07] (0) | 2022.12.07 |
| ★distplot , histplot , twinx(), ticker , axvline()★정규분포 그래프★기초통계학-[Chapter03 - 05] (0) | 2022.12.06 |
| ★DDOF = 1★모/표본분산 , 모/표본표준편차★평균편차★기초통계학-[Chapter03 - 04] (0) | 2022.12.02 |
| np.median★절사평균, 중위수★기초통계학-[Chapter03 - 03] (0) | 2022.12.02 |
★distplot , histplot , twinx(), ticker , axvline()★정규분포 그래프★기초통계학-[Chapter03 - 05]
1. A 데이터프레임 생성
A='30.74 28.44 30.20 32.67 33.29 31.06 30.08 30.62 27.31 27.88 ' \
'26.03 29.93 31.63 28.13 30.62 27.80 28.69 28.14 31.62 30.61 ' \
'27.95 31.62 29.37 30.61 31.80 29.32 29.92 31.97 30.39 29.14 ' \
'30.14 31.54 31.03 28.52 28.00 28.46 30.38 30.64 29.51 31.04 ' \
'27.00 30.15 29.13 27.63 30.87 28.67 27.39 33.20 29.52 30.86 ' \
'34.01 29.41 31.18 34.59 33.35 33.73 28.39 26.82 29.53 32.55 ' \
'30.34 32.44 27.09 29.51 31.36 31.61 31.24 28.83 31.88 32.24 ' \
'31.72 28.34 29.89 30.27 31.42 29.11 29.36 32.24 29.56 31.72 ' \
'30.67 28.85 30.87 27.17 30.85 28.75 25.84 28.79 31.74 34.59 ' \
'32.69 26.23 28.20 31.62 33.48 28.00 33.86 29.22 26.50 30.89'
A = list(map(float , A.split(' ')))
#A = A.(lambda x : round(x ,2))
A[30.740, 28.440, 30.200, 32.670, 33.290, 31.060,30.080,30.620, ···················]
A = pd.DataFrame(A)
A
A.describe()
2. 계급값 & 도수 값 구하기
bins = np.arange(23.5, 37.5 + 0.5 , 0.5)
hist, bins = np.histogram(A, bins)
print('hist : {}'.format(hist))
print('bins : {}'.format(bins))
Steps=[]
for i in range(len(bins)-1):
Steps.append((bins[i+1] - (0.5/2)))
print(Steps)
DOSU = pd.DataFrame({'계급값' : Steps , '도수' : hist})
DOSUhist : [ 0 0 0 0 1 2 2 5 4 9 7 8 8 8 12 7 12 3 3 4 2 1 2 0
0 0 0 0] ==> 도수값
bins : [23.5 24. 24.5 25. 25.5 26. 26.5 27. 27.5 28. 28.5 29. 29.5 30.
30.5 31. 31.5 32. 32.5 33. 33.5 34. 34.5 35. 35.5 36. 36.5 37.
37.5] ==> 계급간격
Steps : [23.75, 24.25, 24.75, 25.25, 25.75, 26.25, 26.75, 27.25, 27.75, 28.25, 28.75, 29.25, 29.75, 30.25, 30.75, 31.25, 31.75, 32.25, 32.75, 33.25, 33.75, 34.25, 34.75, 35.25, 35.75, 36.25, 36.75, 37.25]
==> 계급값_2 ==>계급간격의 절반값

2-1 . 히스토그램 (by matplotlib)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.hist(A, Steps , rwidth = 0.8 , alpha = 0.5)
plt.title('계급 간격 별 도수 막대그래프')
plt.xlabel('계급간격' , fontsize = 14 , labelpad= 14 ,rotation = 0)
plt.ylabel('도수' , fontsize = 14 , labelpad= 14 ,rotation = 0)
plt.xticks(fontsize = 14)
plt.yticks(fontsize = 14)
2-2 . 히스토그램 (by Seaborn)_ x축간격 설정 ticker.MultipleLocator(0.5)
from matplotlib import ticker
fig = plt.figure(figsize=(15,15))
fig.set_facecolor('white')
ax= sns.histplot(A, kde=True) #정규분포 그래프 표시
ax.set_xlim([Steps[0] , Steps[-1]])
ax.xaxis.set_major_locator(ticker.MultipleLocator(0.5)) #x축 간격을 0.5로 설정
plt.show()
2-3 . 도수분포표를 막대그래프로 표현 (by Seaborn)
fig = plt.figure(figsize=(15,15))
fig.set_facecolor('white')
ax = sns.barplot(x= Steps , y =hist)
for i,txt in enumerate(list(hist)):
b = txt
#print(b)
if b == max(list(hist)):
ax.text(i, b+0.2, str(txt)+'개' , ha='center' , color = 'red' , fontweight = 'bold' , fontsize=15)
#어디 막대, 막대기의 위쪽에
else:
ax.text(i, b+0.2, str(txt)+'개' , ha='center' , color = 'dimgray' , fontsize=15 , fontweight = 'bold')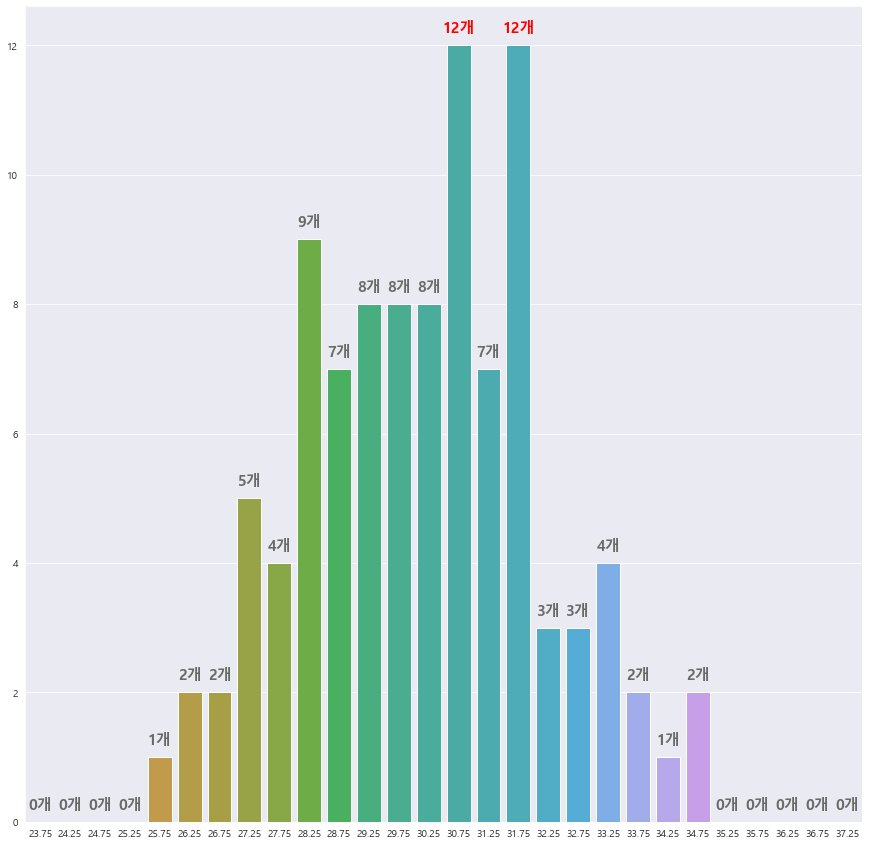
2-4 . 도수분포표를 히스토그램 & 정규분포 표현 (by Seaborn, distplot 사용!!)
fig , ax1 = plt.subplots(figsize= (15,8))
ax1 = sns.distplot(A['data'],bins = 28 , kde=False)
ax1.set_xlim([Steps[0] , Steps[-1]])
ax1.xaxis.set_major_locator(ticker.MultipleLocator(0.5)) #x축 간격을 0.5로 설정
for p in ax1.patches:
#print(p)
ax1.text(x = p.get_x() + p.get_width()/2,
y = p.get_height() + len(A)*0.001,
s = 'X좌표 : \n{}\n {} {}'.format(round(p.get_x(),3),int(p.get_height()),'개'),
#s = f'{(p.get_height()/ len(A)) * 100: 1.1f}개',
ha = 'center')
ax1.set_ylabel('갯수' , fontsize = 14 , labelpad= 14 ,rotation = 0)
ax2 = ax1.twinx() #한 그래프에 두번째 plot 넣기
ax2 = sns.distplot(A['data'],bins = 28 , hist=False , kde=True)
ax2.set_xlim([Steps[0] , Steps[-1]])
ax2.xaxis.set_major_locator(ticker.MultipleLocator(0.5)) #x축 간격을 0.5로 설정
ax2.axes.yaxis.set_visible(False) #y축 없애기
plt.show()
==> X좌표 변경은 불가능한거 같다.
ax1.xaxis.set_major_locator(ticker.MultipleLocator(0.5)) #x축 간격을 0.5로 설정ax1 = sns.distplot(A['data'],bins = 28 , kde=False)==> kde = False 해야 옆 y축 밀도가 아닌 질량으로 변경된다.
2-5 히스토그램 & 정규분포 표현 (by Seaborn, distplot 사용!!)
fig , ax1 = plt.subplots(figsize= (15,8))
ax1 = sns.distplot(A['data'],bins = 28 , kde=False)
ax1.set_xlim([Steps[0] , Steps[-1]])
ax1.xaxis.set_major_locator(ticker.MultipleLocator(0.5)) #x축 간격을 0.5로 설정
for p in ax1.patches:
#print(p)
ax1.text(x = p.get_x() + p.get_width()/2,
y = p.get_height() + len(A)*0.001,
s = 'X좌표 : \n{}\n {} {}'.format(round(p.get_x(),3),int(p.get_height()),'개'),
#s = f'{(p.get_height()/ len(A)) * 100: 1.1f}개',
ha = 'center')
ax1.set_ylabel('갯수' , fontsize = 14 , labelpad= 14 ,rotation = 0)
ax2 = ax1.twinx() #한 그래프에 두번째 plot 넣기
ax2 = sns.distplot(A['data'],bins = 28 , hist=False , kde=True, color='red')
ax2.set_xlim([Steps[0] , Steps[-1]]) #x축 시작 지점과 끝지점 표현
ax2.xaxis.set_major_locator(ticker.MultipleLocator(0.5)) #x축 간격을 0.5로 설정
ax2.axes.yaxis.set_visible(False) #y축 없애기
x_s1 = float(A.mean() - A.std()*1)
x_s2 = float(A.mean() - A.std()*2)
x_s3 = float(A.mean() - A.std()*3)
x_plus_s1 = float(A.mean() + A.std())
x_plus_s2 = float(A.mean() + A.std()*2)
x_plus_s3 = float(A.mean() + A.std()*3)
# 수직선 표현하기
ax2.axvline(x= x_s1, ymin=0 , ymax=1 , color = 'red' , linestyle ='solid' , label ='{}'.format(2))
ax2.text(x_s1 , .19 , f'x-s : {round(x_s1,2)}',fontsize=13)
ax2.axvline(x= x_s2, ymin=0 , ymax=1 , color = 'blue' , linestyle ='solid' , label ='{}'.format(2))
ax2.text(x_s2 , .19 , f'x-2s : {round(x_s2,2)}',fontsize=13)
ax2.axvline(x= x_s3, ymin=0 , ymax=1 , color = 'purple' , linestyle ='solid' , label ='{}'.format(2))
ax2.text(x_s3 , .19 , f'x-3s : {round(x_s3,2)}',fontsize=13)
ax2.axvline(x= x_plus_s1, ymin=0 , ymax=1 , color = 'red' , linestyle ='solid' , label ='{}'.format(2))
ax2.text(x_plus_s1 , .19 , f'x+1s : {round(x_plus_s1,2)}',fontsize=13)
ax2.axvline(x= x_plus_s2, ymin=0 , ymax=1 , color = 'blue' , linestyle ='solid' , label ='{}'.format(2))
ax2.text(x_plus_s2 , .19 , f'x+2s : {round(x_plus_s2,2)}',fontsize=13)
ax2.axvline(x= x_plus_s3, ymin=0 , ymax=1 , color = 'purple' , linestyle ='solid' , label ='{}'.format(2))
ax2.text(x_plus_s3 , .19 , f'x+3s : {round(x_plus_s3,2)}',fontsize=13)
plt.show()

==> 평균 : 30.138
==> 표준편차 : s = 1.991
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 평균,표준편차,분산' 카테고리의 다른 글
| insert() , index★그룹화 자료의 분산과 표준편차★기초통계학-[Chapter03 - 07] (0) | 2022.12.07 |
|---|---|
| 경험적규칙★체비쇼프 정리★기초통계학-[Chapter03 - 06] (0) | 2022.12.06 |
| ★DDOF = 1★모/표본분산 , 모/표본표준편차★평균편차★기초통계학-[Chapter03 - 04] (0) | 2022.12.02 |
| np.median★절사평균, 중위수★기초통계학-[Chapter03 - 03] (0) | 2022.12.02 |
| ★가중평균, 표본평균★기초통계학-[Chapter03 - 02] (1) | 2022.12.02 |
WINDOWS 11에서 MATH INPUT PANEL 을 사용해보자!
Windows 11 업데이트 시 MATH INPUT PANEL 이 사라져 있다.
1. WINDOWS 검색 ==> POWERSHELL "관리자 실행"
2. Get-WindowsCapability -Online | Where-Object {$_.Name -like "*math*"} 입력

2-2. Uninstalled의 경우 Add-WindowsCapability -Online -Name MathRecognizer~~~~0.0.1.0 실행
3. Dism /online /add-capability /capabilityname:MathRecognizer~~~~0.0.1.0 ==> 재설치 명령어
4.

4. MATH INPUT PANEL 은 없어져서 액셀로 하는게 최선의 방법인거 같다 ㅠㅠ

5. 액셀 실행 ==> 삽입 ==> 수식 ==> 잉크 수식 하면 수학식 입력판이 나온다.
'IT에대해 알아보자 > IT인프라' 카테고리의 다른 글
| ★Math Input Pannel★Windows에서 수학식을 입력하여 출력해보자! (0) | 2022.12.01 |
|---|---|
| [Hyper-V] Windows 에서 VMM 사용하기(Hyper-V 언어 및 업데이트)-6 (0) | 2021.10.12 |
| [Hyper-V] Windows 에서 VMM 사용하기(Hyper-V 네트워크 설정)-5 (0) | 2021.10.12 |
| [Hyper-V] Windows 에서 VMM 사용하기(Hyper-V 에 서버 설치)-4 (0) | 2021.10.12 |
| [Hyper-V] Windows 에서 VMM 사용하기(Hyper-V 설치방법)-3 (0) | 2021.10.10 |
★DDOF = 1★모/표본분산 , 모/표본표준편차★평균편차★기초통계학-[Chapter03 - 04]
산포의 척도
==> 평균깊이가 1.2M인 강을 키가 1.7M인 사람이 걸어서 무사히 건널 수 있는지에 대해 생각
==> 강의 평균 깊이가 1.2M 라는 뜻은 1.2M보다 작은 부분도 있지만 1.2M보다 깊은 곳도 있을 수 있다.
==> 평균 깊이만 가지고는 이 강의 특성을 알 수 없다.
1. 산포도(Measure of dispersion)_범위
==> 자료의 흩어진 정도 또는 밀집 정도를 나타내는 척도
EX) A = 240 24 27 30 28 31 22 27 30 25 25 23
B = 24 24 27 30 28 31 22 27 30 25 25 23
집단 A의 최대 자료값 : 240
최소 자료값: 22
범위 : 218
집단 B의 최대 자료값 : 31
최소 자료값 : 22
범위 : 9
==> 범위는 특이값(outlier)에 대해 매우 큰 영향을 받는 척도
2. 평균편차(Mean deviation)
==> 범위는 양 극단의 두 자료 값에 의하여 결정 BUT. 모든 자료 값의 정보를 고려하지 않는다.
==> 평균편차는 각 자료 값과 평균의 편차에 대한 절대값들의 평균

A = 1 2 3 4 5 6 7 7 7 8 9 10 11 12 13
B = 5 6 6 6 7 7 7 7 7 7 7 8 8 8 9
==> A의 평균 편차 : 2.8
==> B의 평균 편차 : 0.67
==> 두 집단의 산술평균: 7
==> 집단 A가 집단 B보다 자료가 더 폭 넓게 분포하고 있음을 알 수 있다.
==> 평균편차의 특징
1. 개개의 자료 값의 정보 반영
2. 범위보다 특이점에 대한 영향 덜 받는다.
3. 절대값을 사용하여 수리적으로 처리 힘들다.
4. 평균편차가 클수록 폭 넓게 분포한다.
EX)[2, 4 , 7 , 3 , 8 , 1 , 2 , 7 , 5 , 5]의 평균편차
A = [2, 4 , 7 , 3 , 8 , 1 , 2 , 7 , 5 , 5]
print(np.mean(A))산술 평균 : 4.4
MD = [abs(round(i-np.mean(A) ,1)) for i in A]
MD = int(sum(MD) /len(A))
MDMD = [2.4, 0.4, 2.6, 1.4, 3.6, 3.4, 2.4, 2.6, 0.6, 0.6]
평균편차 : 2
3. 모분산(Population variance)
==> 모집단을 구성하는 모든 자료값 x1, x2, x3 ········ xN 과 모평균의 편차의 제곱에 대한 평균

EX) 경부고속도로의 나들목 사이 33곳 구간의 거리에 대한 모분산 구하기
뮤 값 = 평균 = 12.208485
xi = 각각의 값
A = '9.59 4.62 0.65 7.75 16.98 11.78 7.24 10.15 25.49 11.44 10.37 9.33 15.04 12.16 16.63 12.06 9.70 12.46 8.05 19.91 5.58 12.48 4.35 16.41 22.53 17.56 18.40 10.86 27.43 7.39 14.57 11.92 2.00'
A = list(map(float , A.split(' ')))
AA = [9.59 4.62 0.65 7.75 16.98 11.78 7.24 10.15 25.49 11.44 10.37 9.33 15.04 12.16 16.63 12.06 9.70 12.46 8.05 19.91 5.58 12.48 4.35 16.41 22.53 17.56 18.40 10.86 27.43 7.39 14.57 11.92 2.00]
var = np.var(A)
varvar = 37.349 (모분산)
std = 루트(37.349) = 6.111 ~ 6.206174 (오차가 있다.) (표본표준편차 와 모표준편차의 차이이기 때문!!)
A = pd.Series(A)
A
A.describe()
==> Describe()의 STD의 의미는 표본표준편차이다!!!!!!!!!!!!!!!!
4. 표본분산(Sample variance)
==> 표본을 구성하는 모든 자료값 x1, x2 , ·······xn 과 표본평균의 편차의 제곱합을 n-1로 나눈 값

==> 모분산은 모집단을 구성하는 모든 자료의 개수인
==> 표본분산은 편차제곱합을 N-1로 나누어야 한다.
특징:
1. 개개의 자료 값의 정보 반영
2. 수리적으로 다루기 쉬움
3. 특이점에 대한 영향 매우 크다. (WHY? 표본이므로 갯수가 적기 때문)
4. 미지의 모분산 추론 위하여 표본 분산 이용
EX) 표본 [6,3,4,2,4] 에 대한 표본분산 구하기
var = np.var(B ,ddof=1) #표본분산 위해서는 ddof =1 설정
var
s**2 = 8.8/4 = 2.2
std= np.std(B ,ddof= 1)
stds = 루트(2.2) = 1.483
※표본분산을 구하기 위해서는 ddof =1 설정해주어야 한다.!!!
5. 모표준편차(Population Standard Deviation) and 표본표준편차(Sample Standard Deviation)
==> 분산의 경우 제곱을 이용하여 표현되므로 자료 값의 단위를 제곱한 단위 사용
==> 해석의 용이함을 위하여 제곱근을 취해준다.
==> 표준편차가 작을수록 자료 값들은 평균 주위로 집중
==> 표준편차가 클 수록 폭넓게 흩어진다.
==> 2개 이상의 자료 집단의 밀집 정도를 비교할 때 사용


EX)A = [9.59 4.62 0.65 7.75 16.98 11.78 7.24 10.15 25.49 11.44 10.37 9.33 15.04 12.16 16.63 12.06 9.70 12.46 8.05 19.91 5.58 12.48 4.35 16.41 22.53 17.56 18.40 10.86 27.43 7.39 14.57 11.92 2.00]
A의 모집단의 모표준편차 : o(오메가) = 루트(37.34) = 6.1114
var2 = np.var(A)
std2 = math.sqrt(var2)
std2var2 = 37.34
o(오메가) = 루트(37.34) = 6.1114
B = [6,3,4,2,4] 의 표본표준편차 구하시오
var = np.var(B ,ddof=1) #표본분산 위해서는 ddof =1 설정
varstd= np.std(B ,ddof= 1)
stds= 루트(2.2) = 1.4832
※표본분산 or 표본표준편차 구할때 ddof =1 설정해주자!!
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 평균,표준편차,분산' 카테고리의 다른 글
| 경험적규칙★체비쇼프 정리★기초통계학-[Chapter03 - 06] (0) | 2022.12.06 |
|---|---|
| ★distplot , histplot , twinx(), ticker , axvline()★정규분포 그래프★기초통계학-[Chapter03 - 05] (0) | 2022.12.06 |
| np.median★절사평균, 중위수★기초통계학-[Chapter03 - 03] (0) | 2022.12.02 |
| ★가중평균, 표본평균★기초통계학-[Chapter03 - 02] (1) | 2022.12.02 |
| ★모평균, 표본평균★중심위치의 척도★기초통계학-[Chapter03 - 01] (0) | 2022.12.01 |
np.median★절사평균, 중위수★기초통계학-[Chapter03 - 03]
1. 절사평균
A = [1,2,3,4,5] 의 산술평균 : 3
B = [1,2,3,4,50]의 산술평균 : 12
==> 산술평균은 특이점(_50_) 과 같이 유무에 따라 많은 영향을 받는다.
==> 특이점 있을경우 특이점 제거한다면 특이점의 영향을 감소시킬 수 있다.
==> 절사평균은 이런 특이점을 제거한 평균 사용
==> 보편적으로 양쪽 끝 5%~10% 절사
EX) 240,24,27,30,28,31,22,27,30,25,25,23 에 대한 평균과 10% 절사평균을 구하라.
A = [240,24,27,30,28,31,22,27,30,25,25,23]
A = sorted(A , reverse=False)
print(A)
print('산술평균 : {}'.format(round(sum(A) / len(A),2)))
i = int(len(A)*0.1)
j = int(len(A) - i)
print(i)
print(j)
B = A[i:j]
print(B)
print('절사평균 : {}'.format(round(sum(B) / len(B),2)))
2. 중위수(Median)
240,24,27,30,28,31,22,27,30,25,25,23
특이점 : 240 ==> 평균에 큰 차이를 보인다.
절사평균 : 27.0
==> 자료를 작은 수부터 크기순으로 나열하여 한가운데에 놓이는 수이다.
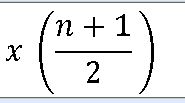
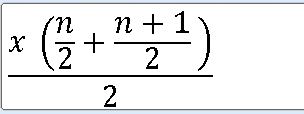
중위수의 위치는 자료 집단의 상대도수다각형의 왼쪽 넓이와 오른쪽 넓이가 동일하게 0.5가 되는 경계값이다.
중위수 특징:
1. 특이점에 대해 전혀 영향을 받지않는다.
2.한 방향으로 치우치고 , 다른 방향으로 긴 꼬리 모양을 갖는 분포를 갖는 경우 평균보다 좋은 중심위치
EX) 240,24,27,30,28,31,22,27,30,25,25,23의 중위수
print(np.median(A))==> 27.0
2. 최빈값(Sample mode)
==> 2 번이상 발생하는 자료 값 중에서 가장 많은 도수를 가지는 자료 값
==> 최빈값은 질적 자료와 양적자료 모두 사용 가능
EX) 240,24,27,30,28,31,22,27,30,25,25,23의 최빈값
from scipy.stats import mode
import collections
b = collections.Counter(A)
print(b)
print(b.keys())
print(b.values())
mode(A) #최빈값 다수일 경우 첫번째 값 반환==> Counter({25: 2, 27: 2, 30: 2, 22: 1, 23: 1, 24: 1, 28: 1, 31: 1, 240: 1})
==> dict_keys([22, 23, 24, 25, 27, 28, 30, 31, 240])
==> dict_values([1, 1, 1, 2, 2, 1, 2, 1, 1])
==> ModeResult(mode=array([25]), count=array([2]))
fig = plt.figure(figsize = (8,8))
ax = plt.plot(figsize= (8,8))
fig.set_facecolor('white')
ax = sns.barplot(x=list(b.keys()) , y = list(b.values()))
ax.set_title('숫자별 빈도수')
ax.set_xlabel('숫자들' , fontsize= 13)
ax.set_ylabel('빈도수' , rotation = 0, fontsize= 13)
print(list(b.values()))
for i,txt in enumerate(list(b.values())):
c = txt
if c == max(list(b.values())):
ax.text(i, c+0.04, str(txt)+'개' , ha='center' , color = 'red' , fontweight = 'bold' , fontsize=17)
#어디 막대, 막대기의 위쪽에
else:
ax.text(i, c+0.05, str(txt)+'개' , ha='center' , color = 'dimgray' , fontsize=13 , fontweight = 'bold')

==> 쌍봉형 또는 여러 개의 봉우리 형태로 나타난다. ==> 쌍봉분포(bimodal distribution) or 다봉분포(Multimodal distribution)
==> 최빈값 1개 ==> 단봉분포(unimodal distribution)
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 평균,표준편차,분산' 카테고리의 다른 글
| 경험적규칙★체비쇼프 정리★기초통계학-[Chapter03 - 06] (0) | 2022.12.06 |
|---|---|
| ★distplot , histplot , twinx(), ticker , axvline()★정규분포 그래프★기초통계학-[Chapter03 - 05] (0) | 2022.12.06 |
| ★DDOF = 1★모/표본분산 , 모/표본표준편차★평균편차★기초통계학-[Chapter03 - 04] (0) | 2022.12.02 |
| ★가중평균, 표본평균★기초통계학-[Chapter03 - 02] (1) | 2022.12.02 |
| ★모평균, 표본평균★중심위치의 척도★기초통계학-[Chapter03 - 01] (0) | 2022.12.01 |
★가중평균, 표본평균★기초통계학-[Chapter03 - 02]
EX) 50명의 청소년들이 일주일 동안 인터넷을 사용한 시간 조사결과
A ='29 30 49 21 39 38 15 39 48 41 50 38 33 40 51 29 31 42 29 69 37 20 49 40 10 49 49 49 35 45 22 45 20 45 30 41 40 38 10 31 47 19 31 21 41 46 28 29 18 28'
A = list(map(int, A.split(' ')))
A[29, 30, 49, 21, 39, 38, 15, 39, 48 · · · · · · · ·]
bins = np.arange(9.5, 72.5 + 9 , 9)
hist, bins = np.histogram(A, bins)
print(hist)
print(bins)
Steps = []
interval = []
for i in range(len(bins)-1):
Steps.append(int(bins[i+1] - (9/2)))
interval.append('{} ~ {}'.format(bins[i] , bins[i+1]))
print(Steps)
print('Steps : {}'.format(Steps)) #계급값
print(interval)
print('interval : {}'.format(interval))
print(len(hist))
print('hist : {}'.format(hist))
print(len(bins))
print('bins : {}'.format(bins))
ratio = []
for i in hist:
ratio.append(round(i/50 ,2))
print('ratio : {}'.format(ratio))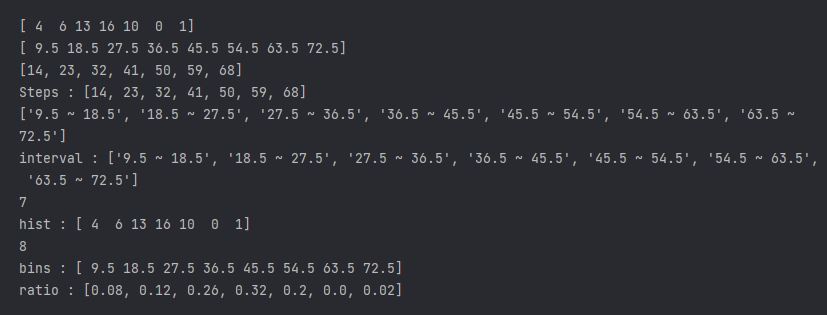
B = pd.DataFrame({'계급간격' : interval ,'도수' : hist , '상대도수' : ratio, '계급값' : Steps} )
B
1. Matplotlib 히스토그램
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
#ax = plt.plot(figsize=(8,8))
plt.hist(A, bins , rwidth = 0.8 , alpha = 0.5)
plt.title('계급 간격 별 도수 막대그래프')
plt.xlabel('계급간격' , fontsize = 14 , labelpad= 14 ,rotation = 0)
plt.ylabel('도수' , fontsize = 14 , labelpad= 14 ,rotation = 0)
plt.xticks(fontsize = 14)
plt.yticks(fontsize = 14)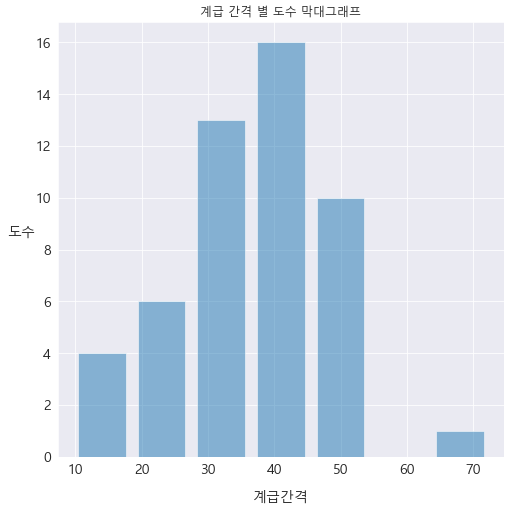
2. Seaborn 히스토그램(막대그래프)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = plt.plot(figsize= (8,8))
ax = sns.barplot(x=B['계급간격'] , y = B['도수'])
for i,txt in enumerate(B['도수']):
b = txt
print(b)
if b == max(B['도수']):
ax.text(i, b+0.4, str(txt)+'개' , ha='center' , color = 'red' , fontweight = 'bold' , fontsize=17)
#어디 막대, 막대기의 위쪽에
else:
ax.text(i, b+0.5, str(txt)+'개' , ha='center' , color = 'dimgray' , fontsize=13 , fontweight = 'bold')
3. 도수 분포표에 따른 가중평균
GazungPyeong = []
for i in range(len(B['계급값'])):
GazungPyeong.append(round(B['계급값'][i] * B['상대도수'][i] ,2))
print(GazungPyeong)
print(sum(GazungPyeong))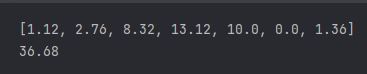
모평균 : 35.48
가중평균 : 36.68
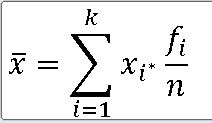
==> 왜 가중평균 ? : 자료에 대해 중심위치를 구하는 데 매우 효과적으로 사용
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 평균,표준편차,분산' 카테고리의 다른 글
| 경험적규칙★체비쇼프 정리★기초통계학-[Chapter03 - 06] (0) | 2022.12.06 |
|---|---|
| ★distplot , histplot , twinx(), ticker , axvline()★정규분포 그래프★기초통계학-[Chapter03 - 05] (0) | 2022.12.06 |
| ★DDOF = 1★모/표본분산 , 모/표본표준편차★평균편차★기초통계학-[Chapter03 - 04] (0) | 2022.12.02 |
| np.median★절사평균, 중위수★기초통계학-[Chapter03 - 03] (0) | 2022.12.02 |
| ★모평균, 표본평균★중심위치의 척도★기초통계학-[Chapter03 - 01] (0) | 2022.12.01 |