전체 글
★연속성 수정 근사확률★추측통계의 X+Y의 평균과 분산★정규분포★기초통계학-[Chapter06 - 연습문제-13]
19. 집에서 학교까지 평균 10분 , 표준편차 1.5분인 정규분포 ==> N (10 , 1.5**2)
1>집에서 학교까지 가는데 12분이상 걸릴 확률
P(X>=12) = P(Z>= (12 -10) / 1.5) = 1 - P(Z<=(12-10)/1.5)
b = scipy.stats.norm.cdf( (12-10) / 1.5)
bb = scipy.stats.norm.cdf( (12-10) / 1.5)
print(1-b)P(X>=12) = 0.091
2>집에서 학교까지 가는데 9분안에 도착할 확률
P(0<=X<=9) = P((0-10) / 1.5 <=Z<= (9 -10) / 1.5) = P(Z<= (9 -10) / 1.5)) - P(Z<=(0-10) / 1.5) =
b = scipy.stats.norm.cdf( -1 / 1.5)
print(b)P(X<=9) = 0.2524
3>집에서 학교까지 가는데 7분이상 11분 안에 도착할 확률
P(7<=X<=11) = P((7-10) / 1.5 <=Z<= (11 -10) / 1.5) ) = P(Z<= (11 -10) / 1.5)) - P(Z<=(7-10) / 1.5) = 0.7247
b = scipy.stats.norm.cdf( 1 / 1.5) - scipy.stats.norm.cdf( (7-10) / 1.5)
print(b)20. 성적이 X ~ N(70,16)인 정규분포, A,B,C,D,F를 15% , 30% , 30% , 15% , 10% 비율로 준다. A,B,C,D의 하한점수
A등급 : P(X>=x_A) = 1- P(X<=x_A) = 0.15
P(Z<= (x_A - 70) /4) = 0.85
b = scipy.stats.norm.ppf(0.85)
print(b)x_A = 4* 1.036 + 70
= 74.144
b = 1- scipy.stats.norm.cdf(0.15)
print(b)B등급 : P(X>=x_B) = 1 -P(X<=x_B) = 0.45
P(Z<= (x_B - 70) /4) = 0.55
b = scipy.stats.norm.ppf(0.55)
print(b)
x_B = 4* (0.1256) + 70
x = sympy.Symbol('x')
equation = (x -70) - (0.1256) *4
b = sympy.solve( equation)
print(b)x_B 70.5024
C등급 : P(X>=x_C) = 1 -P(X<=x_C) = 0.75
P(Z<= (x_B - 70) /4) = 0.25
b = scipy.stats.norm.ppf(0.25)
print(b)x_B = 4*(-0.6744) + 70
x = sympy.Symbol('x')
equation = (x -70) - (-0.6744) *4
b = sympy.solve( equation)
print(b)x_C = 67.3024
D등급 : P(X>=x_D) = 1 -P(X<=x_D) = 0.9
P(Z<= (x_B - 70) /4) = 0.1
b = scipy.stats.norm.ppf(0.1)
print(b)x_D = 4* (-1.28155) + 70
x = sympy.Symbol('x')
equation = (x -70) - (-1.28155) *4
b = sympy.solve( equation)
print(b)x_D = 64.873
21. 고교 3학년 학생 1000명에게 실시한 모의고사에서 국어 X와 수학 Y는 각각 X ~ N(75 ,9) , Y ~ N(68,16) 인 정규분포를 따르고 , 두 성적은 독립
1> 국어점수 X가 82점 이상일 확률
b = 1- scipy.stats.norm.cdf(7/3)
print(b)P(X>=82) = P (Z>= (82-75) / 3) = 1 - P(Z<=(7/3)) = 0.0098
2> 두과목의 점수의 합이 130점이상 , 150점 이하에 해당하는 학생수
X+Y ~ N (75+68 , 9+16) = N(143 , 25)
X-Y ~ N(75-68 , 9 +16)
https://knowallworld.tistory.com/255
★정규분포의 표준정규분포로의 변환★추측통계학-[Chapter06 - 연속확률분포-04]
1. 확률변수 X와 Y에 대한 분산 2. 서로 독립인 확률변수 X와 Y가 정규분포 X ~N(뮤_1 , 분산) , Y~ N(뮤_2 , 분산) 따르는 경우의 추측통계학 EX-01) X는 N(1995 , 144) Y는 N(1755 , 100) 1> X-Y의 확률분포 X-Y ~ N(1995
knowallworld.tistory.com
==> 추측통계 기법 기억하자!!
P(130<= X+Y <=150) = P( (130-143) / 5 <= Z <= (150-143) /5 ) = P(-13/5 <=Z<= 7/5) = P(Z<= 7/5) - P(Z<= -13/5) = 0.9145
b = scipy.stats.norm.cdf(7/5) - scipy.stats.norm.cdf(-13/5)
print(b)1000* 0.9145 = 914.5명
3> 각 과목에서 상위 5%안에 들기 위한 최소점수
P(X>=x_a) = 0.05
P(Z>= (x_a - 75) / 3) = 1- P( Z<= (x_a - 75) / 3) = 0.05
P( Z<= (x_a - 75) / 3) = 0.95
b = scipy.stats.norm.ppf(0.95)
print(b)x_a = 3* 1.644 + 75
x = sympy.Symbol('x')
equation = (x -75) - (1.644) *3
b = sympy.solve( equation)
print(b)x_a = 79.932
=================
P(Y>=y_a) = 0.05
P(Z>= (y_a - 68) / 4) = 1- P( Z<= (y_a - 68) / 4) = 0.05
P( Z<= (y_a - 68) / 4) = 0.95
b = scipy.stats.norm.ppf(0.95)
print(b)y_a = 4* 1.644 + 68
x = sympy.Symbol('x')
equation = (x -68) - (1.644) *4
b = sympy.solve( equation)
print(b)y_a = 74.576
22. X ~ B(20, 0.4)에 대하여 연속성을 수정한 근사확률 구하기. ==> 베르누이 시행
==>연속성 수정 +- 0.5
https://knowallworld.tistory.com/257
이항분포, 푸아송분포,정규분포 기억하기★cdf, pdf 사용법!★정규근사★파스칼★이항분포의 정
1.이항분포의 정규근사 ==> 매회 성공률인 P인 이항 실험을 n번 독립적으로 반복하여 시행할 때 성공의 횟수 ==> 이항분포 https://knowallworld.tistory.com/241 이항분포식★이항실험★이항분포의 평균,분
knowallworld.tistory.com
==> 연속성 수정 참고!
==> P(a<=X <= b) = P(a-0.5 <= X <= b +0.5)
X ~ N(20*0.4 , 20*0.4*0.6) = N(8 , 4.8)
1> P(X<= 10+0.5) = P(Z<= (10+0.5-8)/ 루트(4.8)) = 0.873
b = scipy.stats.norm.cdf((10-8+0.5)/math.sqrt(4.8))
print(b)
2> P(7<=X<= 11)
b = scipy.stats.norm.cdf((11-8+0.5)/math.sqrt(4.8)) - scipy.stats.norm.cdf((6-8+0.5)/math.sqrt(4.8))
print(b)= P(6.5 <= X <= 11.5) = P(Z<= (11.5 -8)/루트(4.8)) - P(Z<= (6.5 - 8)/루트(4.8)) = 0.6981
3> P(X>= 15)
b = 1- scipy.stats.norm.cdf((14-8+0.5)/math.sqrt(4.8))
print(b)= 1 - P(X<=14.5) = 1 - P(Z<= (14.5-8)/루트(4.8) ) = 0.0015
23.5지선다 문제 ==> 100문항
X ~ B(100 , 1/5)
==> X ~ N (20 , 16)
1> 선택한 평균 정답 수
20
2> 정답을 정확히 15개 선택할 근사확률
b = scipy.stats.norm.cdf((15-20+0.5)/4)-scipy.stats.norm.cdf((14-20+0.5)/4)
print(b)P(X=15) = P(14.5 <= X<= 15.5) = P(X<=15.5) - P(X<=14.5) = P(Z <=(15.5 -20 / 4) ) - P(Z <=(14.5 -20 / 4) ) = 0.0457
3>25개 이하로 정답을 선택할 근사확률
b = scipy.stats.norm.cdf((5+0.5)/4)
print(b)P(X<=25) = P(X<=25.5) = P(Z<= (25.5 -20) / 4 ) = 0.9154
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 연속확률변수' 카테고리의 다른 글
★Z값 모르고 넓이는 알때 ppf★Z값 알고 넓이구할때cdf★sympy.solve★기초통계학-[Chapter06 - 연습문제-12]
13. Z ~ N(0,1)에 대하여 P(Z>=z_a) = a이고 X ~ N(뮤 , 분산)
1> P(X<= 뮤 + 표준편차*z_a)
P(Z<= (뮤+표준편차*z_a - 뮤) /표준편차) = a
2>P(뮤 - 표준편차* z_(a/2) <= X <= 뮤 + 표준편차*z_(a/2) )
P(-z_(a/2) <= Z <= Z_(a/2) ) = (P(Z<=z_(a/2) - P(Z<=0)) * 2 = a
14. X ~ N(60,16)
==> 평균(뮤) = 60 , 분산 = 16
1> P(|X-뮤|<= 0.1* 뮤)
a = scipy.stats.norm.cdf(1.5)*2 - 1
a= (P(X-뮤 <= 0.1*뮤) - P(Z<=0) ) * 2 = (P(Z<= (뮤+0.1뮤 - 뮤) / 4 - 0.5) * 2 = ((P(Z<= (0.1뮤)/4) - 0.5 ) * 2 = 2* P(Z<= (1.5) - 1 = 0.8663
2> P(|X-뮤|<= 2.5* 표준편차) = (P(Z<= (2.5 ) -0.5) *2 = 2* P(Z<= 2.5) - 1 = 0.987
a = scipy.stats.norm.cdf(2.5)*2 - 1
a
15. X ~ N(뮤,분산) , P(뮤 - k*표준편차 < X < 뮤+ k*표준편차) = 0.754
P(-k < Z < k) = (P(Z<k) - P(Z<0)) * 2 = 0.754
P(Z<k) = (0.754 + 1) /2 = 0.877
print(1.754 / 2)
b = scipy.stats.norm.ppf(0.877)
b==> k= 1.16
16. Z에 대해 만족하는 z_0
1> P(Z<=z_0) = 0.9986
b = scipy.stats.norm.ppf(0.9986)
b==> 2.988
2> P(Z<=z_0) = 0.0154
==> -2.1596
3> P(0<=Z<=z_0) = 0.3554
P(Z<=z_0) - 0.5 = 0.3554
P(Z<=z_0) = 0.8554
==> z_0 = 1.0598
4> P(-z_0<=Z<=z_0)
= P(Z<=z_0)*2 -1 = 0.9030
P(Z<=z_0) = (1.9030 / 2)
==> z_0 = 1.6595
5> P(-z_0<=Z<=z_0) = 0.2052
P(Z<=z_0)*2 -1 = 0.2052
z_0 = 0.26
6> P(Z>=z_0)
= 1 - P(Z<=z_0) = 0.6915
P(Z<=z_0) = 1 - 0.6915
z_0 = -0.5001
17. X ~ N(10,9) 만족하는 x_0
1> P(X<=x_0) = 0.9986
b = scipy.stats.norm.ppf(0.9986)
bP(Z<= (x_0 - 10) /3) = 0.9986
(x_0 - 10 / 3) = 2.98888
x = sympy.Symbol('x')
print(2.98*3)
equation = (x -10) - 2.98 *3
b = sympy.solve( equation)
print(b)x_0 = 18.94
2> P(X<=x_0) = 0.0154
P(Z<= (x_0 - 10) /3 ) = 0.0154
b = scipy.stats.norm.ppf(0.0154)
bx_0 = -2.159 *3 + 10
#%%
x = sympy.Symbol('x')
equation = (x -10) + 2.1596 *3
b = sympy.solve( equation)
print(b)x_0 = 3.5212
3> P(10<=X<=x_0) = 0.3554
P( (10-10)/3 <= Z<= (x_0 - 10) /3) = 0.3554
P(0<= Z< = (x_0-10)/3) = P(Z<= (x_0 - 10) / 3) - 0.5 = 0.3554
P(Z<= (x_0 -10) /3) ) = 0.8554
b = scipy.stats.norm.ppf(0.8554)
bx_0 = 3*(1.0598) +10
x = sympy.Symbol('x')
equation = (x -10) - 1.0598 *3
b = sympy.solve( equation)
print(b)x_0 = 13.1794
4> P(-x_0<=X<=x_0) = 0.9030
(P(Z<= (x_0 - 10) /3) - P(Z<=0) ) * 2 = 0.9030
P(Z<=(x_0 - 10) /3)) = 0.9030 /2 + 0.5 =
b = scipy.stats.norm.ppf(0.9030 / 2 + 0.5)
bx_0 = 3*(1.6595) + 10
x = sympy.Symbol('x')
equation = (x -10) - 1.6595 *3
b = sympy.solve( equation)
print(b)x_0 = 14.9785
5> P(-x_0 <= X <= x_0) = 0.2052
P(Z<=(x_0 - 10) /3)) = 0.2052 /2 + 0.5
b = scipy.stats.norm.ppf(0.2052 /2 + 0.5)
bx_0 = 3*(0.26) + 10
x = sympy.Symbol('x')
equation = (x -10) - 0.26 *3
b = sympy.solve( equation)
print(b)x_0 = 10.78
6> P(X>= x_0) = 0.6915
1 - P(X<=x_0) = 0.6915
1 - P(Z<=(x_0 - 10) /3)) = 0.6915
P(Z<=(x_0 - 10) /3)) = 1 - 0.6915
b = scipy.stats.norm.ppf(1-0.6915)
bx_0 = 3*(-0.5) + 10
x = sympy.Symbol('x')
equation = (x -10) - (-0.5) *3
b = sympy.solve( equation)
print(b)x_0 = 8.5
18. X ~ N(4,9) 만족
1> P(X<7) = P(Z< (7-4)/3) = P(Z<1) = 0.8413
b = scipy.stats.norm.cdf(1)
b
2> P(4<=X<=x_0) = 0.4750
P(X<=x_0) - p(X<=4) = P(Z<= (x_0 -4 ) /3 ) - P(Z<=0) = 0.4750
P(Z<= (x_0-4)/3) = 0.975
b = scipy.stats.norm.ppf(0.975)
bx_0 = 3* 1.9599 +4
x = sympy.Symbol('x')
equation = (x -4) - (1.9599) *3
b = sympy.solve( equation)
print(b)x_0 = 9.8797
3> P(1<X<x_0) = 0.756
P( (1-4) /3 < Z < (x_0 - 4) /3) = 0.756
P(-1 < Z < (x_0 - 4) /3) = P(Z<(x_0 - 4) /3) - P(Z<-1) = 0.756
b = scipy.stats.norm.cdf(-1)
bP(Z<(x_0 - 4) /3) = 0.1586 + 0.756
b = scipy.stats.norm.ppf(0.1586 + 0.756)
bx_0 = 3* 1.3696 + 4
x = sympy.Symbol('x')
equation = (x -4) - (1.3696) *3
b = sympy.solve( equation)
print(b)x_0 = 8.1088
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 연속확률변수' 카테고리의 다른 글
sympy.solve() 방정식 값구하기★정규분포의 Z값 궁금할땐 ppf 사용!!!★삼각형그리드★평균,분산구하기★연속확률변수★기초통계학-[Chapter06 - 연습문제-11]
10. 확률변수 X의 확률밀도함수가 다음과 같을 때, P(X<=a)=1/4인 상수 a를 구하라. ==> 연속확률변수
f(x) = 2x , 0<=x<=1
0 , otherwise
from sympy import Integral, Symbol , pprint ,solve
x = Symbol('x')
f = 2 * x
f_x_m = f *x
pprint(Integral(f_x_m, x).doit()) #이쁘게 출력
print('===')
mean_x = Integral(f_x_m, (x, (0, 1))).doit()
print("평균 : {}".format(mean_x)) #적분변수 , 아래끝 , 위끝
var_x = Integral(f_x_m *x, (x, (0, 1))).doit() - math.pow(mean_x , 2)
print("분산 : {}".format(var_x))==> Symbol 과 Integral , solve 라이브러리 불러온다!
https://knowallworld.tistory.com/261
균등분포,F-분포 헷갈림★PDF,PPF,CDF★표준정규확률 구할땐 CDF★기초통계학-[Chapter06 - 연습문제-09]
1. 표준정규확률변수 Z에 대한 확률 구하기(CDF!!!) 1> P(Z>=2.05) a = 1- scipy.stats.norm.cdf(2.05) a 0.02018 2> P(Z P(Z>-1.27) a = 1 - scipy.stats.norm.cdf(-1.27) print(a) 0.8979 4> P(-1.02 P(z_a =2.5 , facecolor = 'skyblue') # x값 , y값 ,
knowallworld.tistory.com
균등분포,F-분포 헷갈림★PDF,PPF,CDF★표준정규확률 구할땐 CDF★기초통계학-[Chapter06 - 연습문제-09]
1. 표준정규확률변수 Z에 대한 확률 구하기(CDF!!!) 1> P(Z>=2.05) a = 1- scipy.stats.norm.cdf(2.05) a 0.02018 2> P(Z P(Z>-1.27) a = 1 - scipy.stats.norm.cdf(-1.27) print(a) 0.8979 4> P(-1.02 P(z_a =2.5 , facecolor = 'skyblue') # x값 , y값 ,
knowallworld.tistory.com
==> mean = 인테그랄(범위) x*f(X)
==> var = 인테그랄(범위) x**2*f(x) - 평균의 제곱
#P(X<=a) = P(Z<= (a-평균)/표준편차)) = 1/4
#(a-평균)/표준편차) = X_r
X_r = scipy.stats.norm.ppf(0.25)
print(X_r)
print(var_x)
print(math.sqrt(var_x))
equation = (x- mean_x) / math.sqrt(var_x) - X_r
d = solve(equation)
print(d)P(X<=a) = 0.25 = P(Z<= (a-평균)/(표준편차) )
==> scipy.stats.norm.ppf(0.25) ==> Z값 구할 수 있다!!
==> Z = -0.6744897501960817
==> sympy의 solve 함수 불러온다!!!! ==> 옆에 값이 0이어만 계산이 가능하다.
==> (x- mean_x) / math.sqrt(var_x) - X_r =
a = 0.507687907931844
11. 연속확률변수 X의 확률밀도함수 f(x)가 x축범위가 (0,1) 인 이등변삼각형일 때
import matplotlib.tri as mtri
fig = plt.figure(figsize=(15,8))
x = np.array([0,1,2]) #삼각형의 x좌표
y = np.array([0,1 , 0]) #삼각형의 y좌표
triangles = [[0,1,2]] #삼각형의 점 개수
triang = mtri.Triangulation(x,y , triangles)
plt.title("삼각 그리드")
plt.triplot(triang , 'ko-')
plt.fill_between(x , x , 0 , where = (x<= 1) & (x>=0) , color = 'orange')
plt.fill_between(x , -x+2 , 0 , where = (x>=1) & (x<= 2) )
plt.xlim(-0.1 , 2.1)
plt.ylim(-0.1 , 1.6)
plt.text(0.5 , 0.6 , 'y = x' , fontsize = 13 , rotation = 33)
plt.text(1.5 , 0.5 , 'y = -x+2' , fontsize = 13 , rotation = -33)
plt.show()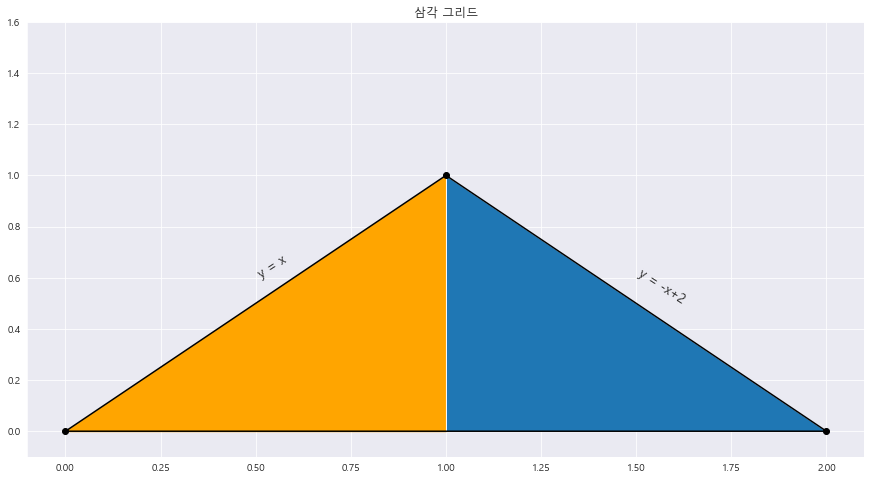
==> 삼각그리드 그리기
1> 상수 k값 구하기
k = sympy.Symbol('k')
sol_k = 2*k*(1/2) -1 # k * 2 * 1/2
k_sol = solve(sol_k)
print(k_sol)k =1
2> P(X<=0.6) = 0.6 * (0.6) /2 = 0.18
from sympy import Integral, Symbol , pprint ,solve
x = Symbol('x')
f_1 = x
f_2 = -x +2
f_x_1_m = f_1 *x
f_x_2_m = f_2 *x
mean_x = Integral(f_x_1_m, (x, (0, 1))).doit() + Integral(f_x_2_m, (x, (1, 2))).doit()
print("평균 : {}".format(mean_x)) #적분변수 , 아래끝 , 위끝
var_x = Integral(f_x_1_m*x, (x, (0, 1))).doit() + Integral(f_x_2_m*x, (x, (1, 2))).doit() - math.pow(mean_x, 2)
print("분산 : {}".format(var_x)) #적분변수 , 아래끝 , 위끝평균 : 1
분산 : 0.166666666666667
x_0_6 = round((0.6-(mean_x)) / math.sqrt(var_x),8)
x_0 = round( (0-mean_x) / math.sqrt(var_x) , 4)
print(x_0_6)
print(x_0)
print(scipy.stats.norm.cdf(-0.97979590))-0.97979590
-2.4495
0.16359343818253824
==> 오차발생 추후 생각해보자
3> P(0.5<=X<=1.5) = (1-0.5) * 0.5 / 2 * 2 + (1 * 0.5) = 0.25 + 0.5 = 0.75
x_0_1_5 = round((1.5-(mean_x)) / math.sqrt(var_x),8)
x_0_5 = round( (0.5-mean_x) / math.sqrt(var_x) , 4)
print(x_0_1_5)
print(x_0_5)
print(scipy.stats.norm.cdf(1.2247) - scipy.stats.norm.cdf(-1.2247) )1.22474487
-1.2247
0.7793117258581086
P(X <=1.5) - P(X<=0.5) = 0.7793 ==> 오차발생
4> P(1.2<= X<=2) =(2-1.2) * 0.8 / 2 = 0.8 * 0.8 / 2 = 0.32
x_0_2 = round((2-(mean_x)) / math.sqrt(var_x),8)
x_0_1_2 = round( (1.2-mean_x) / math.sqrt(var_x) , 4)
print(x_0_2)
print(x_0_1_2)
print(scipy.stats.norm.cdf(2.4494) - scipy.stats.norm.cdf(0.4899) )P(1.2<= X<=2) = P(X<=2) - P(X<=1.2) = 0.3049 ==> 오차발생
12. 확률밀도함수에 대한 확률 구하기
a_x= np.arange(0,20,.1) # len(a_x) = 20
a_y = np.full((1,len(a_x)) , 0.02) #1행 20열값을 0.02로 가득채워라
print(a_y)
A = pd.DataFrame([a_x , *a_y])
A= A.T
a_x= np.arange(20,30,.1) # len(a_x) = 20
a_y = np.full((1,len(a_x)) , 0.04) #1행 20열값을 0.02로 가득채워라
B= pd.DataFrame([a_x , *a_y])
B = B.T
a_x= np.arange(30,41,.1) # len(a_x) = 20
a_y = np.full((1,len(a_x)) , 0.02) #1행 20열값을 0.02로 가득채워라
C= pd.DataFrame([a_x , *a_y])
C = C.T
A = pd.concat([A,B,C]).reset_index()
A = A.iloc[ : , 1:]
A
1> P(X>=35) = 0.1
fig = plt.figure(figsize=(15,8))
# ax = sns.distplot(x = A[0] , y=A[1])
ax= sns.lineplot(x= A[0] , y= A[1])
ax.set_xlim(-1 , 45)
ax.set_ylim(0 , 0.05)
ax.set_xlabel('경기에참여하는 시간' , fontsize = 12)
ax.set_ylabel('확률밀도함수 f(x)' , fontsize= 12 , rotation=0 , labelpad = 20)
ax.fill_between(A[0] , A[1] , 0 , where = (A[0]>=35))
area = (40-35) * 0.02
ax.text(29 , 0.015 , 'P(X>=35) = {}'.format(area) , fontsize= 13)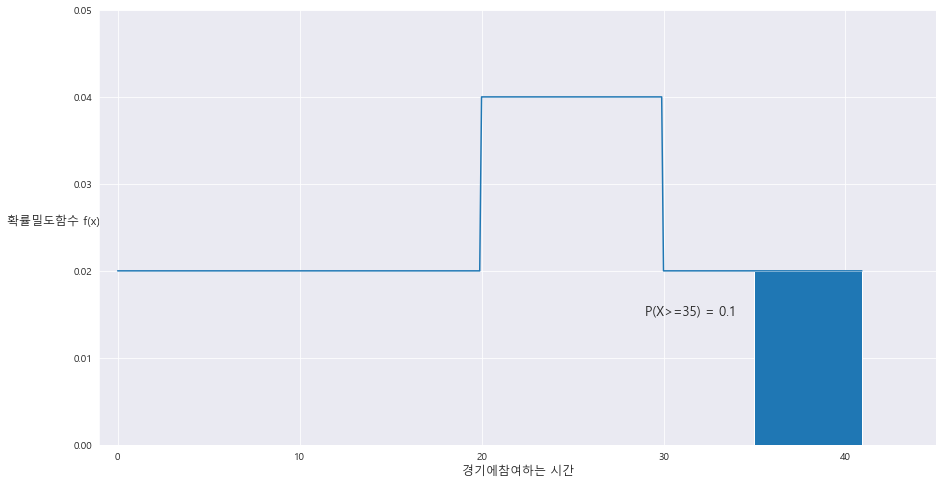
2> P(X<=25) = 0.6
fig = plt.figure(figsize=(15,8))
# ax = sns.distplot(x = A[0] , y=A[1])
ax= sns.lineplot(x= A[0] , y= A[1])
ax.set_xlim(-1 , 45)
ax.set_ylim(0 , 0.05)
ax.set_xlabel('경기에참여하는 시간' , fontsize = 12)
ax.set_ylabel('확률밀도함수 f(x)' , fontsize= 12 , rotation=0 , labelpad = 20)
ax.fill_between(A[0] , A[1] , 0 , where = (A[0]<=25))
area = (25-20) * 0.04 + (20*0.02)
ax.text(26 , 0.015 , 'P(X<=25) = {}'.format(round(area,2)) , fontsize= 13)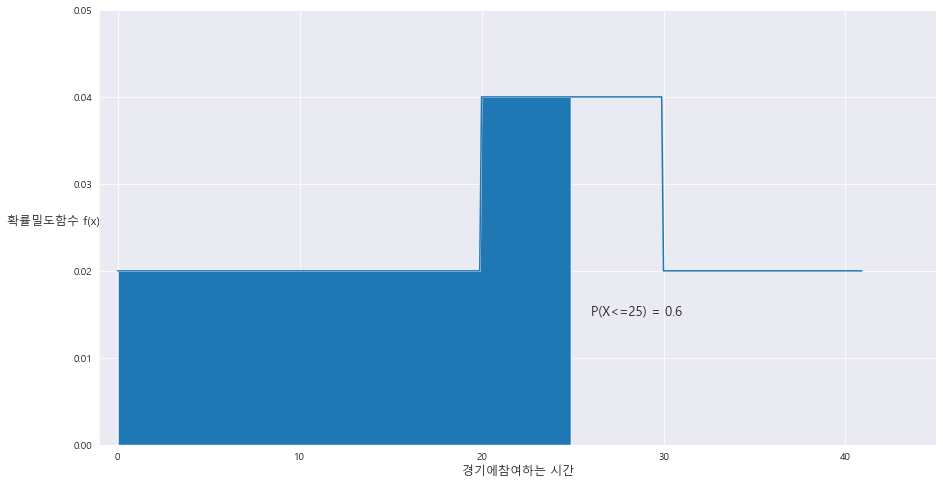
3> P(15<=X<=35) = 0.6
fig = plt.figure(figsize=(15,8))
# ax = sns.distplot(x = A[0] , y=A[1])
ax= sns.lineplot(x= A[0] , y= A[1])
ax.set_xlim(-1 , 45)
ax.set_ylim(0 , 0.05)
ax.set_xlabel('경기에참여하는 시간' , fontsize = 12)
ax.set_ylabel('확률밀도함수 f(x)' , fontsize= 12 , rotation=0 , labelpad = 20)
ax.fill_between(A[0] , A[1] , 0 , where = (A[0]<=35) & (A[0]>=15))
area = (30-20) * 0.04 + ((35-30)*0.02) + ((20-15) *0.02)
ax.text(8 , 0.015 , 'P(15<=X<=35) = {}'.format(round(area,2)) , fontsize= 13)
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 연속확률변수' 카테고리의 다른 글
★균등분포★scipy.stats.uniform.pdf(x= , loc= , scale=)★np.where()★평균_분산구할때_오차줄이기★기초통계학-[Chapter06 - 연습문제-10]
7. 1.5V 건전지는 1.45V에서 1.65V 사이에서 균등분포를 이룬다.
https://knowallworld.tistory.com/252
sympy INTEGRAL,Symbol,pprint★scipy.stats.UDF_균등분포★stats.PDF_확률밀도함수★기초통계학-[Chapter06 - 연속
1. 연속확률변수(Continous Random Variable) ==> 확률변수가 취할 수 있는 모든 값, 상태공간이 어떤 구간으로 나타나는 확률변수 의미 ==> 확률변수 X가 취할 수 있는 모든 값이 유한구간 [a,b] or [(0, 무한
knowallworld.tistory.com
1> 임의로 하나 선정 ==> 기대되는 전압(E(X) ) 과 표준편차(루트(V(X)))
X ~ U(1.45, 1.65)
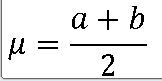
print( (1.45 + 1.65) / 2)print(np.mean(np.arange(min,max, .01)))==> x축의 간격들을 평균처리
==> 1.55

print( math.pow(1.65 - 1.45,2) / 12)print(np.var(np.arange(min,max, .01)))==> x축의 간격들을 분산처리!!!
==> 0.0033
2>건전지 전압이 1.5V 보다 작을 확률
P(1.45<=X<=1.5) = 0.25
#1.5V 건전지는 1.45V에서 1.65V 사이에서 균등분포를 이룬다.
min , max = 1.45, 1.65
# x_2 = linspace(min-1 , max+1 , 100)
x_2 = np.arange(min-.2 , max+.2 , .01)
print(x_2)
y = scipy.stats.uniform.pdf( x = x_2 , loc = min , scale = max-min)
print(y)
print(len(y[np.where(y != 0.)])) #np.where 활용==> np.where 조건절로 원하는 값 추출 가능(0. 아닌것들 추출)
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 5. 5. 5. 5.
5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
20
fig = plt.figure(figsize=(12, 8))
ax = sns.lineplot(x = x_2 , y= y)
ax.set_title('균등분포(Uniform Distribution)')
ax.set_xlabel('X' , fontsize= 15)
ax.set_ylabel('Y' , fontsize= 15 , rotation = 0 , labelpad = 12)
a = scipy.stats.uniform.pdf( x = 1.5 , loc = 1.45 , scale = 1.65-1.45) #scipy.stats.uniform.pdf( x = 1.5 , loc = min , scale = max-min)
print(a)
ax.vlines(1.5 , ymin = 0 , ymax = a , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.fill_between(x_2 , a , 0 , where = (x_2<= 1.5001) & (x_2>= 1.445)) #오차있으므로 신경 끄자.
area = (1.5 - 1.45)*a #넓이 구하기!!!!!
print(area)
ax.text(1.51 , 3, 'P(1.45=<X<=1.5)' + f"= {round(area,4)}",fontsize=15)==> scipy.stats.uniform.pdf( x = 어디까지 확률을 구할것인가, loc= 균등분포에서 제일 작은값 , scale = 균등분포 제일 끝값끼리의 차)

==> 중간에 빈칸들은 np.arange()값을 세분화 시키면 사라진다.
x_2 = np.arange(min-.2 , max+.2 , .001)
y = scipy.stats.uniform.pdf(x = x_2 , loc = 1.45 , scale = 1.65-1.45)
print(y)
fig = plt.figure(figsize=(12, 8))
ax = sns.lineplot(x = x_2 , y= y)
ax.set_title('균등분포(Uniform Distribution)')
ax.set_xlabel('X' , fontsize= 15)
ax.set_ylabel('Y' , fontsize= 15 , rotation = 0 , labelpad = 12)
a = scipy.stats.uniform.pdf( x = 1.5 , loc = 1.45 , scale = 1.65-1.45) #scipy.stats.uniform.pdf( x = 1.5 , loc = min , scale = max-min)
print(a)
ax.vlines(1.5 , ymin = 0 , ymax = a , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.fill_between(x_2 , a , 0 , where = (x_2<= 1.5) & (x_2>= 1.45)) #오차있으므로 신경 끄자.
area = (1.5 - 1.45)*a #넓이 구하기!!!!!
print(area)
ax.text(1.51 , 3, 'P(1.45=<X<=1.5)' + f"= {round(area,4)}",fontsize=15)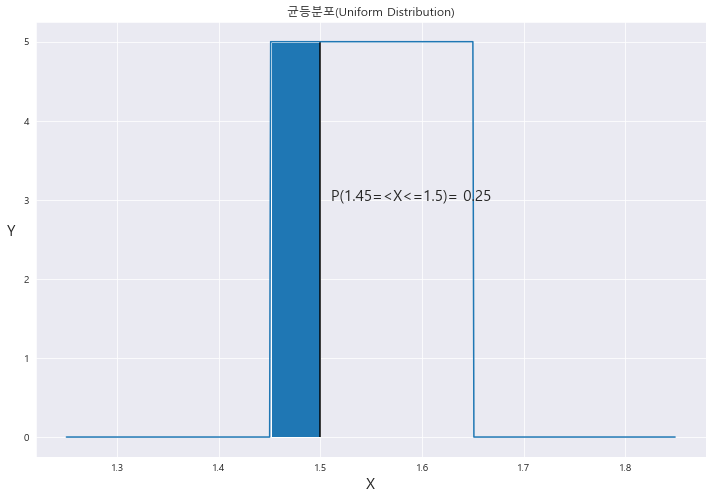
3>10개의 건전지가 들어있는 상자 안에 1.5V보다 전압이 낮은 건전지의 수의 평균과 분산 ==> 베르누이 시행
https://knowallworld.tistory.com/241
이항분포식★이항실험★이항분포의 평균,분산★베르누이시행★기초통계학-[Chapter05 - 이산확률
1. 이항분포 ==> 많이 사용하는 확률 모형 : 이항분포, 푸아송분포 , 초기하분포 1. 이항실험(Bionomial Experiment) ==> 실험은 N번의 시행 ==> 실험 결과는 성공(S) , 실패(F) ==> 성공 확률 : p , 실패 확률 : q
knowallworld.tistory.com
1.5V 보다 작을 확률 = 0.25
X ~ B(10 , 0.25)
E(X) = 10* 0.25 = 2.5
V(X) = 2.5 * 0.75 = 1.875
4> 1.5V 보다 낮은 전압을 가진 건전지가 4개 이상 들어있을 확률 ==> 이항분포 , 이항정리 잘 기억!
https://knowallworld.tistory.com/256
[PYTHON]_코테에서도 쓰일_조합_계산_파스칼의 삼각형_시간복잡도(이항정리, 이항계수) 사용하기!!
1. itertools.combination 사용하기 https://knowallworld.tistory.com/146 [Python] 순열, 조합, 중복순열, 중복조합(itertools이용한 백트래킹) https://knowallworld.tistory.com/228 Permutations()★순열,조합,중복순열,중복조합★
knowallworld.tistory.com
P(Y>=4) = 1- P(Y<3) =
f(x=3) = 10C4 * (0.25**3) * (0.75**7)
res = 0
for i in range(4):
a = len(list(itertools.combinations(np.arange(10) , i)))
print(a)
b = math.pow(0.25 , i) * (math.pow(0.75 , 10-i))
c = a*b
print(c)
res+=c
print(1- res)0.22412490844726562
8. 버스는 오후 1시부터 5시까지 40분 간격, 버스 기다리는 시간은 0에서 40분까지 균등하게 분포를 이룬다.
1> 버스를 기다리는 시간에 대한 확률 밀도함수
f(x) = 0.025 (0<x<40)
0 (otherwise)
2>기다리는 시간의 평균과 표준편차
means = np.mean(x[np.where((x>= 0) & (x<=40))])
#np.where 사용시 ndarray로 한번더 묶어줘야한다.
print(means)
vars = np.var(x[np.where((x>= 0) & (x<=40))])==> np.where 사용시 ==> array의 변수로 리스트화 하여 묶어줘야한다!!!
E(X) = 20
V(X) = 133.3325
print("what?! {}".format(np.std(np.arange(0,40,.1))))
print("what?! {}".format(np.var(np.arange(0,40,.1))))==> 1단위일때 1/10 단위로 np.arange()처리하면 오차를 줄일 수 있다!!!
표준편차 = 루트(140) = 11.547
3> 15분 이상 기다릴 확률
fig = plt.figure(figsize= (15,8))
ax = sns.lineplot(x= x , y= y)
ax.hlines(y= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , xmin = 0-2 , xmax =45)
ax.vlines(x= 15 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')
ax.fill_between(x , y , 0 , where = (x<= 40) & (x>= 15)) #오차있으므로 신경 끄자.
ax.text(-8 , scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , "y = {}".format(round(scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min),7)), fontsize = 14)
#area = P(X>=15) = 1 - P(X<=15) ===> 균등분포는 연속확률분포다!!! 이산확률분포로 생각하면 안된다!!
area = 1 - (scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) *15)
ax.text(5 ,0.020 , "P(X>=15) = {}".format(round(area,3)), fontsize = 14)==> 균등분포는 연속확률분포이다!!!! P(X>=15) = 1-P(X<15) 이다!!!
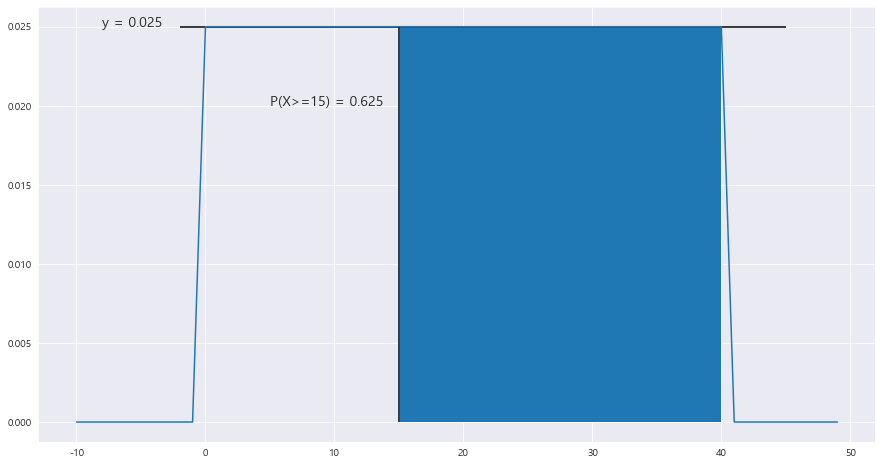
P(X>=15) = 0.625
4> 기다리는 시간이 5분에서 10분 사이일 확률
fig = plt.figure(figsize= (15,8))
ax = sns.lineplot(x= x , y= y)
ax.hlines(y= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , xmin = 0-2 , xmax =45)
ax.vlines(x= 10 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')
ax.vlines(x= 5 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')
ax.fill_between(x , y , 0 , where = (x<= 10) & (x>= 5)) #오차있으므로 신경 끄자.
ax.text(-8 , scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , "y = {}".format(round(scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min),7)), fontsize = 14)
#area = P(5<=X<=10) = P(X<=10) - (X<=4)
area = (scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) *10) - (scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) *5)
ax.text(15 ,0.020 , "P(5<=X<=10) = {}".format(round(area,3)), fontsize = 14)==> 균등분포는 연속확률분포이다!!!! P(5<=X<=10) = P(X<=10) - P(X<5) 이다!!!
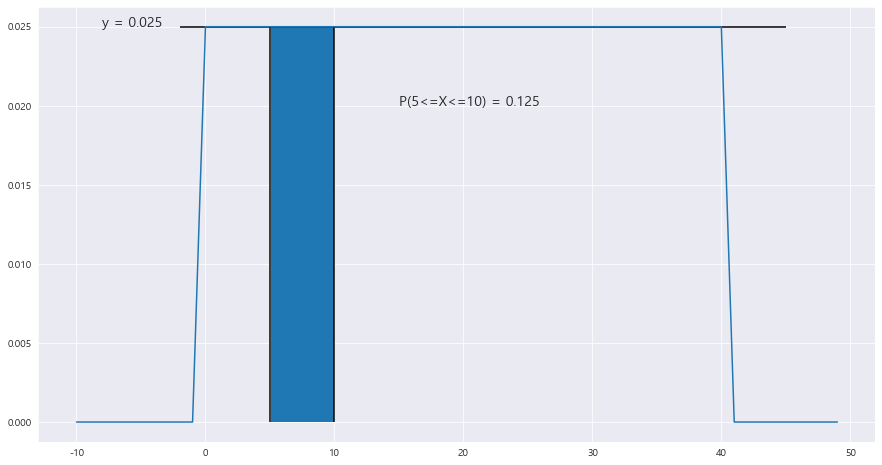
P(5<=X<=10) = P(X<=10) - P(X<=5) = 0.125
9. 연간 1인당 지출하는 보험료는 최소 25만원부터 최대 300만원 사이의 균등분포
1> 보험료로 지출하는 평균 금액과 표준편차를 구하라.
min , max = 25 , 300
x = np.arange(min - 25 , max + 25 , 1)
y = scipy.stats.uniform.pdf(x=x , loc= min , scale = max-min)
print(y)
print("평균 지출금액 : {}".format(np.mean( x[np.where( (x>=25) & (x<=300))])))
print("표준편차 지출금액 : {}".format(round(np.std(np.arange(min,max,.1)),3)))평균 지출금액 : 162.5
표준편차 지출금액 : 79.386
2> 무작위로 한 사람 선정, 이사람이 연간 150만원 이상 지출할 확률
P(X>=150) = 1- P(X<150) = 0.545
fig = plt.figure(figsize= (15,8))
ax = sns.lineplot(x= x , y= y)
ax.hlines(y= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , xmin = min-10 , xmax =310)
#
ax.vlines(x= 150 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')
# ax.vlines(x= 5 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')
#
ax.fill_between(x , y , 0 , where = (x>= 150)) #오차있으므로 신경 끄자.
ax.text(0-15 , 0.0034 , "y = {}".format(round(scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min),7)), fontsize = 14)
#
#area = 1- P(25<=X<150)
area = 1- (scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) *(150-25))
#
#
ax.text(95 ,0.0034 , "P(X>=150) = {}".format(round(area,3)), fontsize = 14)==> x축의 시작이 25부터 인점 주목하자!!!!!

3> 무작위로 한 사람 선정, 이사람이 연간 50만원 이상 , 150만원 이하로 지출할 확률
P(50<=X<=150) = P(X<=150) - P(X<=50) = 0.3636
fig = plt.figure(figsize= (15,8))
ax = sns.lineplot(x= x , y= y)
ax.hlines(y= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , xmin = min-10 , xmax =310)
#
ax.vlines(x= 150 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')
ax.vlines(x= 50 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')
#
ax.fill_between(x , y , 0 , where = (x<= 150) & (x>=50)) #오차있으므로 신경 끄자.
ax.text(0-15 , 0.0034 , "y = {}".format(round(scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min),7)), fontsize = 14)
#
#area = P(X<=150) - P(X<=50)
area = (scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) *(150-25)) - (scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) *(50-25))
#
#
ax.text(155 ,0.0034 , "P(50<=X<=150) = {}".format(round(area,4)), fontsize = 14)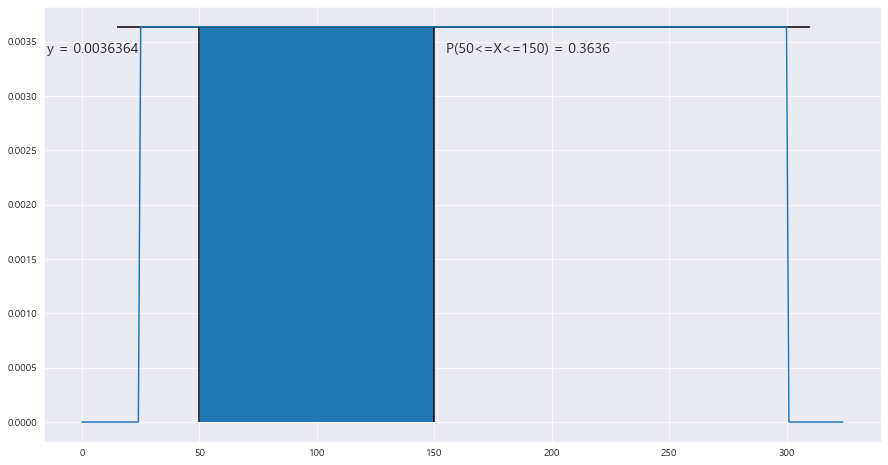
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 연속확률변수' 카테고리의 다른 글
[외교부 인턴 일지- d+109 2022.12.23]데이터 분석 청년인재 양성 사업
기초통계의 늪에 빠졌다.
이번주 T-분포, 카이제곱분포 , F-분포에 대해 알아보았다.
농협은행 시험이 2주 남았다.
이번주부터 SQL 4문제씩 매일, 알고리즘 2문제씩 풀어야한다. 필기도 풀어야한다! 미쳤다!!!
기초통계는 주말(24일)에 Chapter 07까진 했음 좋겠다.
'인턴일지 > 외교부_일지' 카테고리의 다른 글
| [외교부 인턴 일지- d+128 2022.01.08]데이터 분석 청년인재 양성 사업 (0) | 2023.01.08 |
|---|---|
| [외교부 인턴 일지- d+115 2022.12.26]데이터 분석 청년인재 양성 사업 (0) | 2022.12.29 |
| [외교부 인턴 일지- d+100 2022.12.14]데이터 분석 청년인재 양성 사업 (0) | 2022.12.14 |
| [외교부 인턴 일지- d+86 2022.11.30]데이터 분석 청년인재 양성 사업 (0) | 2022.12.01 |
| [외교부 인턴 일지- d+85 2022.11.29]데이터 분석 청년인재 양성 사업 (0) | 2022.11.29 |
★TO_CHAR('열이름' , 'YYYY-MM-DD')★SELECT★흉부외과 또는 일반외과 의사 목록 출력하기[프로그래머스 ORACLE SQL]
https://school.programmers.co.kr/learn/courses/30/lessons/132203
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
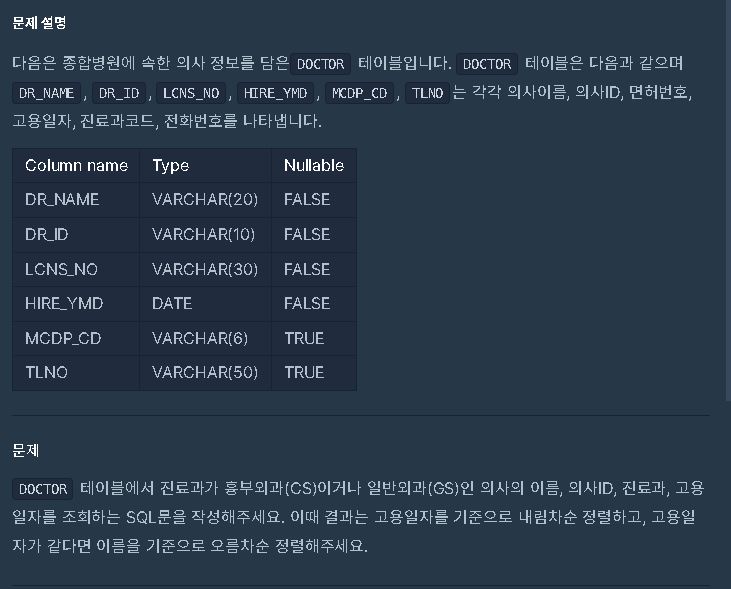
SELECT DR_NAME, DR_ID,MCDP_CD , TO_CHAR(HIRE_YMD , 'YYYY-MM-DD') AS HIRE_YMD FROM DOCTOR
WHERE MCDP_CD IN ('CS' , 'GS')
ORDER BY HIRE_YMD DESC , DR_NAME ASC==> IN
==> TO_CHAR 형식 기억하자!
'SQL > SELECT' 카테고리의 다른 글
| [프로그래머스 ORACLE SQL]조건에 맞는 회원수 구하기★TO_CHAR()쓰임새★VER3.0 (0) | 2023.06.21 |
|---|---|
| VER2.0★범위지정시 BETWEEN★FROM절 서브쿼리★조건에 맞는 회원수 구하기[프로그래머스 ORACLE SQL] (0) | 2023.01.04 |
| ★VER2.0★[프로그래머스 ORACLE SQL]오프라인/온라인 판매 데이터 통합하기 (0) | 2023.01.04 |
| ★GROUP BY 2개 열 사용★[프로그래머스 ORACLE SQL]재구매가 일어난 상품과 회원 리스트 구하기 (0) | 2023.01.04 |
| [프로그래머스 ORACLE SQL]인기있는 아이스크림★정렬★ (0) | 2022.10.27 |
균등분포,F-분포 헷갈림★PDF,PPF,CDF★표준정규확률 구할땐 CDF★기초통계학-[Chapter06 - 연습문제-09]
1. 표준정규확률변수 Z에 대한 확률 구하기(CDF!!!)
1> P(Z>=2.05)
a = 1- scipy.stats.norm.cdf(2.05)
a0.02018
2> P(Z<1.11)
a = scipy.stats.norm.cdf(1.11)
print(a)0.8665
3> P(Z>-1.27)
a = 1 - scipy.stats.norm.cdf(-1.27)
print(a)0.8979
4> P(-1.02<=Z<=1.02)
a = ( scipy.stats.norm.cdf(1.02) - scipy.stats.norm.cdf(0) ) *2
print(a)0.6922
2.. X~ N(5,4)
https://knowallworld.tistory.com/254
정규분포의 표준정규분포로의 변환★기초통계학-[Chapter06 - 연속확률분포-03]
1. 정규분포와 표준정규분포의 관계 =========================== ==> P(z_a =2.5 , facecolor = 'skyblue') # x값 , y값 , 0 , x= 2.5) = P(Z 박테리아의 수가 75마리 이상 103마리 이하일 확률 P(75
knowallworld.tistory.com
1> P(X>=4.5)
a = 1 -scipy.stats.norm.cdf(-0.25)
print(a)==> P(Z>= (4.5 -5) / (루트(4) ) = P(Z>= -0.25) = 0.5987
2> P(X<6.5)
a = scipy.stats.norm.cdf(0.75)
print(a)==> P(Z < 6.5-5 / (루트(4)) = P(Z < 0.75) = 0.7733
3>P(X<=2.5)
a = scipy.stats.norm.cdf(-1.25)
print(a)==> P(Z < 2.5-5 / (루트(4)) = P(Z < -1.25) = 0.1056
4>P(3<=X<=7)
a = (scipy.stats.norm.cdf(1) - scipy.stats.norm.cdf(0)) * 2
print(a)P( (3-5)/루트(4) <= Z <= (7-5)/루트(4) ) = P(-1 <= Z<= 1) = 0.6826
3.. V~ x**2(10) ==> 카이제곱 분포(자유도)
https://knowallworld.tistory.com/258
★scipy.stats.chi2().ppf()★matplotlib 수학식표현★카이제곱분포★정규분포★기초통계학-[Chapter06 - 연
1. 카이제곱분포 ==> 카이제곱분포는 정규모집단의 모분산에 대한 통계적 추론에 사용 ==> n개의 서로 독립인 표준정규확률변수 Z_1 ,Z_2 ,···· Z_n 에 대하여 확률변수의 확률분포를 자유도(degree of
knowallworld.tistory.com
1> 97.5% 백분위수 x**2_0.025
X = np.arange(0,30 ,.01)
fig = plt.figure(figsize = (15,8))
dof = 10
ax = sns.lineplot(X , scipy.stats.chi2(dof).pdf(X))
X_l = scipy.stats.chi2(dof).ppf(0.025) #==> 1.644
X_r = scipy.stats.chi2(dof).ppf(1- 0.025)
ax.fill_between(X , scipy.stats.chi2(dof).pdf(X) , 0 , where = (X<=X_l) | (X>=X_r))
area = scipy.stats.chi2(dof).cdf(X_l) #넓이 구하기!!!!!
print(area)
ax.text(4 , .015, 'P(X <' + r'$\chi^2_{0.025}$)' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(2, .002), xytext=(4 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_l, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_l) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_l + 1, .002, r'$\chi^2_L= {}$'.format(round(X_l,2)) ,fontsize=15)
area = 1- scipy.stats.chi2(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(24 , .015, 'P(X >' + r'$\chi^2_{0.025}$)' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(22, .002), xytext=(24 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.chi2(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 4, .002, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)==> CDF는 넓이 구하기!
==> PPF를 통하여 Z값(원하는 분포값) 얻을 수 있다.

2> P(V > x_0) = 0.995를 만족
P(V<= x_0) = 0.005 (넓이)
==> ppf를 통하여 P(V < X**2_0.005) = P(V< 2.1558) = 0.005
==> 넓이는 cdf로 , ppf로 x_0값 투입 시켜 Z값, V값등을 얻어내자!
x_0 = 2.16
4. T~ t(10) ==> t 분포(자유도)
https://knowallworld.tistory.com/259
★scipy.stats.t(자유도).ppf()★t-분포★기초통계학-[Chapter06 - 연속확률분포-07]
1. T-분포(Chi-square Distribution) ==> T-분포는 모분산이 알려지지 않은 정규모집단의 모평균에 대한 추론 ==>서로 독립인 표준정규화확률변수 Z와 자유도 n인 카이제곱 확률변수 V에 대하여 정의 ==> T ~
knowallworld.tistory.com
1> 95%백분위수 t_0.05
X = np.arange(-5,5 ,.01)
fig = plt.figure(figsize = (15,8))
dof = 10
ax = sns.lineplot(X , scipy.stats.t(dof).pdf(X))
X_l = scipy.stats.t(dof).ppf(0.05) #==> 1.644
X_r = scipy.stats.t(dof).ppf(1- 0.05)
ax.fill_between(X , scipy.stats.t(dof).pdf(X) , 0 , where = (X<=X_l) | (X>=X_r))
area = scipy.stats.t(dof).cdf(X_l) #넓이 구하기!!!!!
print(area)
ax.text(-4, .05, 'P(V <' + r'$\chi_{0}$)' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(-2.6, .004), xytext=(-3, .03) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_l, ymin= 0 , ymax= scipy.stats.t(dof).pdf(X_l) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_l + 0.4, .004, r'$\chi^2_L= {}$'.format(round(X_l,2)) ,fontsize=15)
area = 1- scipy.stats.t(dof).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(4 , .02, 'P(V >' + r'$\chi_{0}$)' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(3.5, .002), xytext=(4 , .014) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.t(dof).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r-1 , .002, r'$\chi^2_R= {}$'.format(round(X_r,2)) ,fontsize=15)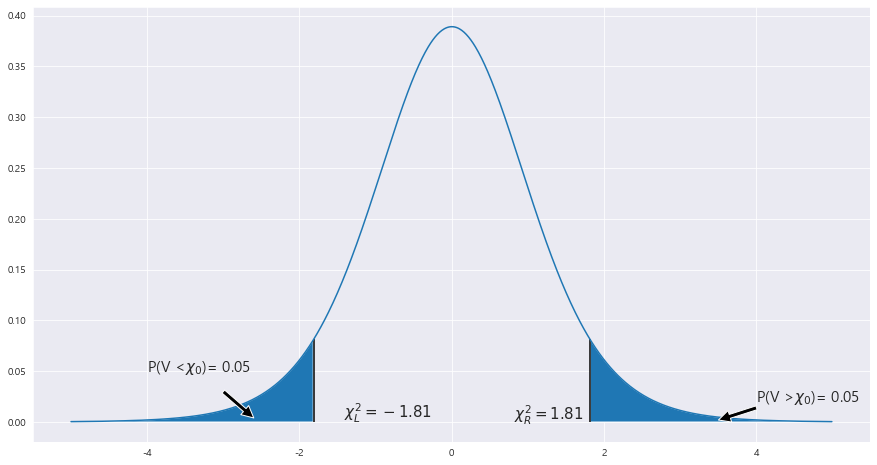
X_R = 1.81
2> P(T<=t_0) = 0.995
X = np.arange(-5,5 ,.01)
fig = plt.figure(figsize = (15,8))
dof = 10
ax = sns.lineplot(X , scipy.stats.t(dof).pdf(X))
X_l = scipy.stats.t(dof).ppf(.995) #==> 1.644
# X_r = scipy.stats.t(dof).ppf(1- 0.05)
ax.fill_between(X , scipy.stats.t(dof).pdf(X) , 0 , where = (X<=X_l))
area = scipy.stats.t(dof).cdf(X_l) #넓이 구하기!!!!!
print(area)
ax.text(-4, .05, 'P(T <' + r'$\chi_{0}$)' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(-2.6, .004), xytext=(-3, .03) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_l, ymin= 0 , ymax= scipy.stats.t(dof).pdf(X_l) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_l + 0.4, .004, r'$\chi^2_L= {}$'.format(round(X_l,2)) ,fontsize=15)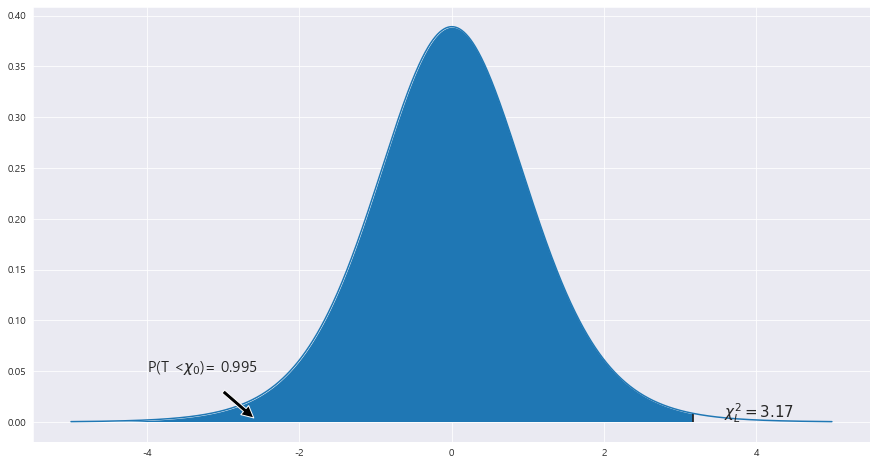
t_0 = 3.17
5. F~ F(8 , 6) ==> F 분포(자유도 1 , 자유도 2)
https://knowallworld.tistory.com/260
★scipy.stats.f(자유도1 , 자유도 2).pdf()★F-분포★기초통계학-[Chapter06 - 연속확률분포-08]
1. F-분포(F-distribution) ==> 서로 독립인 두 모집단의 모분산이 동일한지 아닌지를 통계적으로 추론 ==> 서로 독립인 두 확률변수 F ~ F(m , n) X = np.arange(0,10, .01) fig = plt.figure(figsize = (15,8)) dof = [[5,8] , [2
knowallworld.tistory.com
1> f_0.01 , 8 , 6
X = np.arange(0,10 ,.01)
fig = plt.figure(figsize = (15,8))
dof = [8,6]
ax = sns.lineplot(X , scipy.stats.f(dof[0] , dof[1]).pdf(X))
X_r = scipy.stats.f(dof[0] , dof[1]).ppf(1- 0.01) #==> 1.644
ax.fill_between(X , scipy.stats.f(dof[0] , dof[1]).pdf(X) , 0 , where = (X>=X_r))
area = scipy.stats.f(dof[0] , dof[1]).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(7, .12, 'P(F <' + r'$f_{0.01 , 8 , 6}$)' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(8.1, .005), xytext=(7.1, .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.f(dof[0] , dof[1]).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r + 0.4, .004, r'$f_{0.01, 8 , 6}' + '= {}$'.format(round(X_r,2)) ,fontsize=15)
b = ['F(8,6)']
plt.legend(b , fontsize= 13)
f_0.01,8,6 = 8.1
2>f_0.05,8,6
X = np.arange(0,10 ,.001)
fig = plt.figure(figsize = (15,8))
dof = [8,6]
ax = sns.lineplot(X , scipy.stats.f(dof[0] , dof[1]).pdf(X))
X_r = scipy.stats.f(dof[0] , dof[1]).ppf(1-0.05) #==> 상위 1%일때 x좌표
ax.fill_between(X , scipy.stats.f(dof[0] , dof[1]).pdf(X) , 0 , where = (X>=X_r))
area = 1- scipy.stats.f(dof[0] , dof[1]).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(7, .12, 'P(F >' + r'$f_{0.05 , 8 , 6}$)' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(8.1, .005), xytext=(7.1, .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.f(dof[0] , dof[1]).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r - 1.4, .004, r'$f_{0.05, 8 , 6}' + '= {}$'.format(round(X_r,2)) ,fontsize=15)
b = ['F(8,6)']
plt.legend(b , fontsize= 13)
f_0.05,8,6 = 4.15
3>f_0.90,8,6
X = np.arange(0,10 ,.001)
fig = plt.figure(figsize = (15,8))
dof = [8,6]
ax = sns.lineplot(X , scipy.stats.f(dof[0] , dof[1]).pdf(X))
X_r = scipy.stats.f(dof[0] , dof[1]).ppf(1-0.9) #==> 상위 1%일때 x좌표
ax.fill_between(X , scipy.stats.f(dof[0] , dof[1]).pdf(X) , 0 , where = (X>=X_r))
area = 1- scipy.stats.f(dof[0] , dof[1]).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(7, .12, 'P(F >' + r'$f_{0.9 , 8 , 6}$)' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(8.1, .005), xytext=(7.1, .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.f(dof[0] , dof[1]).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r + 0.04, .05, r'$f_{0.9, 8 , 6}' + '= {}$'.format(round(X_r,2)) ,fontsize=15)
b = ['F(8,6)']
plt.legend(b , fontsize= 13)
f_0.90,8,6 = 0.37
4>f_0.99,8,6
X = np.arange(0,10 ,.001)
fig = plt.figure(figsize = (15,8))
dof = [8,6]
ax = sns.lineplot(X , scipy.stats.f(dof[0] , dof[1]).pdf(X))
X_r = scipy.stats.f(dof[0] , dof[1]).ppf(1-0.99) #==> 상위 1%일때 x좌표
ax.fill_between(X , scipy.stats.f(dof[0] , dof[1]).pdf(X) , 0 , where = (X>=X_r))
area = 1- scipy.stats.f(dof[0] , dof[1]).cdf(X_r) #넓이 구하기!!!!!
print(area)
ax.text(7, .12, 'P(F >' + r'$f_{0.99 , 8 , 6}$)' + f"= {round(area,4)}",fontsize=15)
plt.annotate('' , xy=(8.1, .005), xytext=(7.1, .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= X_r, ymin= 0 , ymax= scipy.stats.f(dof[0] , dof[1]).pdf(X_r) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(X_r + .2, .05, r'$f_{0.99, 8 , 6}' + '= {}$'.format(round(X_r,2)) ,fontsize=15)
b = ['F(8,6)']
plt.legend(b , fontsize= 13)
f_0.99,8,6 = 0.16
==> 답지가 틀렸다 100%
6. X~ U(-2 , 2) ==> 균등분포
https://knowallworld.tistory.com/252
sympy INTEGRAL,Symbol,pprint★scipy.stats.UDF_균등분포★stats.PDF_확률밀도함수★기초통계학-[Chapter06 - 연속
1. 연속확률변수(Continous Random Variable) ==> 확률변수가 취할 수 있는 모든 값, 상태공간이 어떤 구간으로 나타나는 확률변수 의미 ==> 확률변수 X가 취할 수 있는 모든 값이 유한구간 [a,b] or [(0, 무한
knowallworld.tistory.com
1> X의 확률밀도함수
-2<=X<=2 ==> 1/4
otherwise ==> 0
2> X의 평균과 분산
3>
확률 평균-표준편차 이상 평균+표준편차 이하
x = Symbol('x')
f_x = 1/4
f_x_m = f_x * x
print(f_x_m)
mean_1 = Integral(f_x_m, (x,(-2 , 2))).doit()
print("평균 : {}".format(mean_1))
f_x_v = f_x_m * x
print(f_x_v)
vars_1 = Integral(f_x_v , (x,-2,2)).doit() - mean_1**2
print("분산 : {}".format(vars_1))
ratio = Integral(f_x , (x,mean_1-math.sqrt(vars_1),mean_1+math.sqrt(vars_1))).doit()
print("확률 평균-표준편차 이상 평균+표준편차 이하는 {}이다.".format(ratio))0.25*x
평균 : 0
0.25*x**2
분산 : 1.33333333333333
확률 평균-표준편차 이상 평균+표준편차 이하는 0.577350269189626이다.
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 연속확률변수' 카테고리의 다른 글
★scipy.stats.f(자유도1 , 자유도 2).pdf()★F-분포★기초통계학-[Chapter06 - 연속확률분포-08]
1. F-분포(F-distribution)
==> 서로 독립인 두 모집단의 모분산이 동일한지 아닌지를 통계적으로 추론
==> 서로 독립인 두 확률변수


F ~ F(m , n)



X = np.arange(0,10, .01)
fig = plt.figure(figsize = (15,8))
dof = [[5,8] , [2,3] , [23,23] , [18,25], [11,7]]
print(dof[0][0])
for i in dof:
ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
b = ['F({},{})'.format(i,j) for i,j in dof]
plt.legend(b , fontsize= 15)==> scipy.stats.f(자유도 1, 자유도 2)

==> 일반적으로 왼쪽으로 치우치고, 오른쪽으로 긴 꼬리를 갖는다.(양의 왜도)
EX-01) 자유도 7과 10인 F-분포에서 중심확률이 0.9인 두 임계점 f_L , f_R를 구하라
꼬리확률 = 0.1
f_0.95,7,10
f_0.05,7,10
X = np.arange(0,10, .01)
fig = plt.figure(figsize = (15,8))
dof = [[7,10]]
print(dof[0][0])
for i in dof:
ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
b = ['F({},{})'.format(i,j) for i,j in dof]
X_r = scipy.stats.f(dof[0][0], dof[0][1]).ppf(0.95)
X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(0.05)
ax.fill_between(X, scipy.stats.f(dof[0][0],dof[0][1]).pdf(X) , where = (X>=X_r) | (X<=X_l) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
ax.vlines(X_r , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_r) , color = 'black')
ax.vlines(X_l , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_l) , color = 'black')
ax.annotate('' , xy=(X_l -0.02 , 0.1) , xytext=(X_l + 0.5 , 0.1) , arrowprops = dict(facecolor = 'black'))
ax.text(X_l + 0.5 , 0.1 , r'$P(F\leqq f_{0.95,7,10})$' + f'= {0.05}' , fontsize = 14)
ax.annotate('' , xy=(X_r +0.3 , 0.01) , xytext=(X_r + 0.3 , 0.2) , arrowprops = dict(facecolor = 'black'))
ax.text(X_r + 0.3 , 0.21 , r'$P(F\geqq f_{0.05,7,10})$' + f'= {0.05}' , fontsize = 14)
ax.text(X_l + 0.05 , 0.01 , r'$f_{0.95,7,10}$)' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(0.05) ,2)}' ,fontsize = 13)
ax.text(X_r - 1.3 , 0.01 , r'$f_{0.05,7,10}$)' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(0.95) , 2)}' ,fontsize = 13)
plt.legend(b , fontsize= 15)==> 수학 표현식 geqq , leqq
==> ppf 사용!
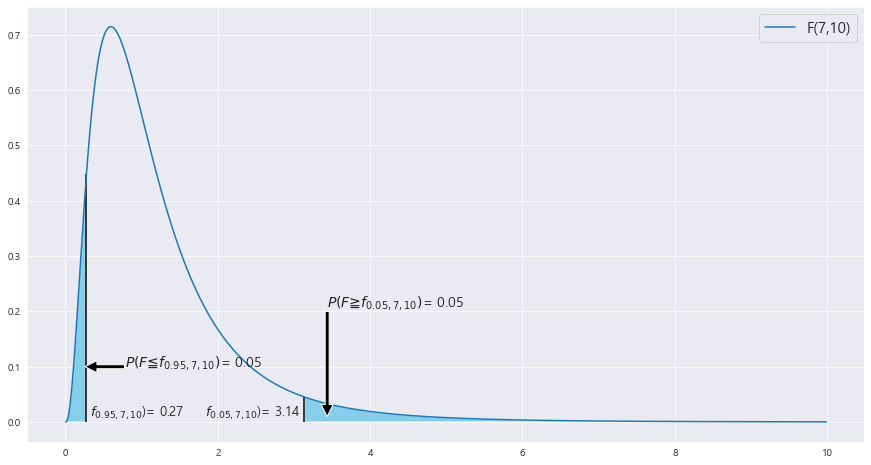
f_L = 0.27
f_R = 3.14
EX-02) F ~ F(4,5)
X = np.arange(0,10, .01)
fig = plt.figure(figsize = (15,8))
dof = [[4,5]]
print(dof[0][0])
for i in dof:
ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
b = ['F({},{})'.format(i,j) for i,j in dof]
X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(1-0.95)
X_r = scipy.stats.f(dof[0][0], dof[0][1]).ppf(1-0.025)
ax.fill_between(X, scipy.stats.f(dof[0][0],dof[0][1]).pdf(X) , where = (X>=X_r) | (X<=X_l) , facecolor = 'skyblue') # x값 , y값 , 0 , x조건 인곳 , 색깔
ax.vlines(X_r , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_r) , color = 'black')
ax.vlines(X_l , ymin = 0 , ymax = scipy.stats.f(dof[0][0],dof[0][1]).pdf(X_l) , color = 'black')
area = 1- scipy.stats.f(dof[0][0],dof[0][1]).cdf(X_r)
area_2 = scipy.stats.f(dof[0][0],dof[0][1]).cdf(X_l)
ax.annotate('' , xy=(X_r +2 , 0.01) , xytext=(X_r + 2 , 0.2) , arrowprops = dict(facecolor = 'black'))
ax.text(X_l + 0.1 , 0.21 , r'$P(F\leqq f_{0.95,4,5})$' + f'= {round(area_2,2)}' , fontsize = 14)
ax.annotate('' , xy=(X_l +0.05 , 0.2) , xytext=(X_l + 0.3 , 0.2) , arrowprops = dict(facecolor = 'black'))
ax.text(X_r + 0.3 , 0.21 , r'$P(F\geqq f_{0.025,4,5})$' + f'= {round(area , 2)}' , fontsize = 14)
ax.text(X_r + 0.05 , 0.01 , r'$f_{0.025,4,5}$' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1-0.025) ,2)}' ,fontsize = 13)
ax.text(X_l +0.1 , 0.01 , r'$f_{0.95,4,5}$' + f'= {round(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1-0.95) , 2)}' ,fontsize = 13)
plt.legend(b , fontsize= 15)==>헷갈린다.
==> F분포의 경우 왼쪽 꼬리확률이 0.05인 임계점 f_0.95,4,5
==> 오른쪽 꼬리확률이 0.05인 임계점 f_0.05,4,5

1> f_0.025 , 4 , 5
==> 7.39
2> f_0.95,4,5
==> 0.16
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용