전체 글
-
[PYTHON - 머신러닝_K-MEAN 군집화]★엘보우 기법2023.01.27
[PYTHON - 머신러닝_캐글_피처 스케일링]★min-max 정규화★표준화(Standardization)
1. 피처 스케일링
==> 서로 다른 피처 값의 범위(최댓값 - 최솟값) 이 일치하도록 조정하는 작업
2. min-max 정규화(min-max normalization)
==> 피처 값의 범위를 0~1로 조정하는 기법이다.
https://knowallworld.tistory.com/373
[PYTHON - 머신러닝_KNN알고리즘]★value_counts()★고윳값 판단★결측치★스케일링
1. 고윳값 판단 data['class'].unique() # 목표 변수의 고윳값 출력 ==> 0과 1로 이루어진 이진변수가 아닌 3개이상으로 이루어진 범주형 변수 ==> array([0,1,2]) data['class'].nunique() # 고윳값의 갯수 ==> 와인을 3
knowallworld.tistory.com

height_weight_dict = {'키' : [1.7 , 1.5 , 1.8] , '몸무게' : [75,55,60]}
df = pd.DataFrame(height_weight_dict , index = ['광일' , '혜성' , '덕수'])
print(df)
from sklearn.preprocessing import MinMaxScaler
# min-max 정규화 객체 생성
scaler = MinMaxScaler()
# min-max 정규화 적용
df_scaled = scaler.fit_transform(df)
df_scaled
3. 표준화(Standardization)
==> 평균이 0 , 분산이 1이 되도록 피처 값을 조정하는 기법
==> min-max 정규화와 다르게 표준화는 상한과 하한이 없다.
https://knowallworld.tistory.com/373
[PYTHON - 머신러닝_KNN알고리즘]★value_counts()★고윳값 판단★결측치★스케일링
1. 고윳값 판단 data['class'].unique() # 목표 변수의 고윳값 출력 ==> 0과 1로 이루어진 이진변수가 아닌 3개이상으로 이루어진 범주형 변수 ==> array([0,1,2]) data['class'].nunique() # 고윳값의 갯수 ==> 와인을 3
knowallworld.tistory.com
==> 데이터에 아웃라이어가 존재할 때 아웃라이어의 영향을 받는다. 평균 0, 분산 1이 되게끔 분포시키기 때문에, 데이터의 기존 분포 형태가 사라지고 정규분포를 따르는 결과물을 가져온다.

from sklearn.preprocessing import StandardScaler
# StandardScaler 객체 생성
scaler = StandardScaler()
# 표준화 적용
df_scaled = scaler.fit_transform(df)
df_scaled
출처 : 머신러닝·딥러닝 문제해결 전략
(Golden Rabbit , 저자 : 신백균)
※혼자 공부용
'머신러닝 > 캐글_머신러닝_이론' 카테고리의 다른 글
| [PYTHON - 머신러닝_캐글_모델]★선형 회귀 모델★ (0) | 2023.01.31 |
|---|---|
| [PYTHON - 머신러닝_캐글_교차검증]★K-폴드 교차검증★충화 K-폴드 교차검증★folds.split(data)★ (1) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_데이터 인코딩]★LabelEncoder★One-Hot-Encoder (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_분류와 회귀]★회귀 평가지표★분류 평가지표★ROC, AUC★RMSE (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_기본 그래프]★regplot()회귀 선★barplot() vs countplot()★ (0) | 2023.01.31 |
[PYTHON - 머신러닝_캐글_데이터 인코딩]★LabelEncoder★One-Hot-Encoder
머신러닝 모델은 문자 데이터를 인식하지 못한다. 이를 문자로 구성된 범주형 데이터는 숫자로 바꿔야 한다.
==> 범주형 데이터를 숫자 형태로 바꾸는 작업을 데이터 인코딩이라고 한다.
1. 레이블 인코딩
==> 범주형 데이터를 숫자로 일대일 매핑해주는 인코딩 방식
from sklearn.preprocessing import LabelEncoder #레이블 인코더
fruits = ['사과' , '블루베리' , '바나나' , '귤' , '블루베리' , '바나나' ,'바나나' , '사과']
label_encoder = LabelEncoder() # 레이블 인코더 생성
fruits_label_encoed = label_encoder.fit_transform(fruits)
print('레이블 인코딩 적용 후 데이터 ' , fruits_label_encoed)레이블 인코딩 적용 후 데이터 [3 2 1 0 2 1 1 3]
2. One-Hot encoding
https://knowallworld.tistory.com/372
[PYTHON - 머신러닝_로지스틱선형회귀]★로지스틱 선형회귀★상관관계★원-핫 인코딩★정확도★
1. 로지스틱 회귀 ==> 로지스틱 회귀 또한 선형 회귀처럼 기본 분석 모델이다. ==>선형 회귀 분석은 연속된 변수를 예측하는 반면 , 로지스틱 회귀 분석은 Yes/No처럼 2가지로 나뉘는 분류 문제를 다
knowallworld.tistory.com
==> 여러 값중 하나만 활성화하는 인코딩이다.
==> 레이블 인코딩의 문제(서로 가까운 숫자를 비슷한 데이터로 판단하는 문제)를 해결한다.


from sklearn.preprocessing import LabelEncoder , OneHotEncoder #레이블 인코더 , 원 핫 인코더
fruits = ['사과' , '블루베리' , '바나나' , '귤' , '블루베리' , '바나나' ,'바나나' , '사과']
label_encoder = LabelEncoder() # 레이블 인코더 생성
onehot_encoder = OneHotEncoder()
fruits_label_encoed = label_encoder.fit_transform(fruits) # 레이블 인코더 적용
fruits_onehot_encoed = onehot_encoder.fit_transform(fruits_label_encoed.reshape(-1,1))
# reshape(-1,1) 메서드를 이용해 2차원으로 바꾸었다.
print('원-핫 인코딩 적용 후 데이터 ' , fruits_onehot_encoed.toarray())
원-핫 인코딩 적용 후 데이터 [[0. 0. 0. 1.]
[0. 0. 1. 0.]
[0. 1. 0. 0.]
[1. 0. 0. 0.]
[0. 0. 1. 0.]
[0. 1. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 0. 1.]]
pd.get_dummies(fruits)
출처 : 머신러닝·딥러닝 문제해결 전략
(Golden Rabbit , 저자 : 신백균)
※혼자 공부용
'머신러닝 > 캐글_머신러닝_이론' 카테고리의 다른 글
| [PYTHON - 머신러닝_캐글_모델]★선형 회귀 모델★ (0) | 2023.01.31 |
|---|---|
| [PYTHON - 머신러닝_캐글_교차검증]★K-폴드 교차검증★충화 K-폴드 교차검증★folds.split(data)★ (1) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_피처 스케일링]★min-max 정규화★표준화(Standardization) (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_분류와 회귀]★회귀 평가지표★분류 평가지표★ROC, AUC★RMSE (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_기본 그래프]★regplot()회귀 선★barplot() vs countplot()★ (0) | 2023.01.31 |
[PYTHON - 머신러닝_캐글_분류와 회귀]★회귀 평가지표★분류 평가지표★ROC, AUC★RMSE
1. 분류(Classification)
==> 어떤 대상을 정해진 범주에 구분해 넣는 작업
ex) 서점의 IT도서 코너에 IT도서가 있다. 종업원은 IT책을 어느 코너에 꽂아둘까? ==> 책 내용에 IT용어가 많다. ==> IT 코너에 꽂아준다. ==> 책의 내용(피처, feature)을 토대로 IT도서(타깃, target)라고 판단한다.
==> 분류 작업
==> 분류 작업할 타깃값은 범주형 데이터
==> 타깃값이 2개 : 이진분류
==> 타깃값이 3개: 다중분류
2. 분류 평가지표
1> 오차행렬(Confusion matrix) :
실제 타깃값과 예측한 타깃값이 어떻게 매칭되는가
https://knowallworld.tistory.com/377
[PYTHON - 머신러닝_XGBoost]★pd.options.display.max_columns★정밀도, 재현율, F1-score
1. 부스팅 알고리즘 ==> 랜덤 포레스트는 각 트리를 독립적으로 만드는 알고리즘 ==> 서로 관련 없이 생성한다. ==> 부스팅은 순차적으로 트리를 만들어 이전 트리로부터 학습한 내용이 다음 트리
knowallworld.tistory.com
[[1291 74]
[ 151 110]]
| 실제값 \ 예측값 | 0 | 1 |
| 0 | 1291 | 74 |
| 1 | 151 | 110 |
==> 실제로 매칭이 안되었는데, 실제로 매칭이 안되었다고 예측한 경우 : 1291 건 (참 양성)
==> 실제로 매칭이 되었는데, 실제로 매칭되었다고 예측한경우 : 110 건(참 음성)
==> 실제로 매칭이 안되었는데, 매칭이 되었다고 예측한 경우 : 74 건(제 1종 오류)
==> 실제로 매칭이 되었는데 , 매칭이 안되었다고 예측한 경우 : 151 건 (제 2종 오류)
정밀도(precision)은 1로 예측한 경우 중, 얼마만큼이 실제로 1인지를 나타낸다.
==> 양성을 양성으로 판단 / (양성을 양성으로 판단 + 1종오류) ==> 1 종오류가 중요하면 정밀도에 주목
재현율(recall)은 실제로 1 중에, 얼마만큼을 1로 예측했는지를 나타낸다.
==> 양성을 양성으로 판단/ (양성을 양성으로판단 + 2종오류) ==> 2 종오류가 중요하면 재현도에 주목
F1-점수(F1-score)은 정밀도와 재현율의 조화평균을 의미한다.
==> 2 * (정밀도 * 재현율) / (정밀도 + 재현율) ==> 1 종오류, 2종오류 중요한 오류가 없다면 F1-SCORE 활용
2> 로그손실(logloss) :
분류 문제에서 타깃값을 확률로 예측할 때 기본적으로 사용하는 평가지표이다. ==> 값이 작을 수록 좋다.
3> ROC(Receiver Operating Characteristic)곡선과 AUC(Area Under the Curve) :
==> ROC : 참 양성 비율에 대한 거짓 양성 비율
민감도_참 양성 비율(TPR) = TP(참양성) / (TP(참 양성) + FN(거짓 음성) ) = 재현율
==> 실제 1인 것중 얼마만큼 제대로 1로 예측되었는지 ==> 1에 가까울 수록 좋다.
==> AUC : ROC 곡선 아래 면적
3. 회귀(Regression)
독립변수(Independent variable) : 영향을 미치는 변수
종속변수(dependent variable) : 영향을 받는 변수
==> 독립변수와 종속변수 간 관계를 모델링하는 방법이다.
==> 회귀의 종속변수(타깃값)이 범주형 데이터가 아닌 수치형 데이터이다.
https://knowallworld.tistory.com/371
[PYTHON - 머신러닝_선형회귀]★선형회귀★seaborn 타원만들기★모델 평가방법 RMSE , R**2★model.coef_(
1. 선형회귀 ==> 가장 기초적인 머신러닝 모델 ==> 여러가지 데이터를 연속형 변수인 목표 변수를 예측해 내는 것이 목적이다. ==> 몸무게, 나이 , BMI, 성별 등의 데이터를 활용하여 연속형 변수를
knowallworld.tistory.com

==> 독립변수 하나(x)와 종속변수 하나(Y) 사이의 관계를 나타낸 모델링 기법

==> 독립변수 여러개와 종속변수 하나(Y) 사이의 관계를 나타낸 모델링 기법
==> 회귀문제에서는 주어진 독립변수(피처) 와 종속변수(타깃값) 사이의 관계를 기반으로 회귀계수(쉐타)를 찾아야한다.
4. 회귀 평가지표
==> 회귀모델을 훈련해 최적의 회귀계수 구하기 위해서는 예측값과 실제값의 차이(오차)를 최소화해야한다.
㉠ MAE : 평균 절대 오차 , 실제 타깃값과 예측 타깃값 차의 절대값 평균
㉡ MSE : 평균 제곱 오차 , 실제값과 예측값 사이의 오차를 제곱한 뒤 이에 대한 평균 계산

㉢ RMSE : 평균 제곱근 오차 , MSE에 제곱근을 취한 값

㉣ MSLE : MSE에서 타깃값에 로그값을 취한 값 ==> y에 1을 더한 이유는 로그값이 음의 무한대가 되는 상황 방지

㉤ RMSLE :MSLE에 제곱근을 취한 값

㉥ R**2 : 결정계수

==> 예측 타깃값의 분산 / 실제 타깃값의 분산 ==> 1에 가까울 수록 모델 성능이 좋다.
true = np.array([1,2,3,2,3,5,4,6,5,6,7,8,8]) # 실제값
preds = np.array([1,1,2,2,3,4,4,5,5,7,7,6,8]) # 예측값
MAE = mean_absolute_error(true , preds)
MSE = mean_squared_error(true , preds)
RMSE = np.sqrt(MSE)
MSLE = mean_squared_log_error(true , preds)
RMSLE = np.sqrt(mean_squared_log_error(true , preds))
R2 = r2_score(true, preds)
print(f'MAE :\t {MAE:.4f}')
print(f'MSE :\t {MSE:.4f}')
print(f'RMSE :\t {RMSE:.4f}')
print(f'MSLE :\t {MSLE:.4f}')
print(f'RMSLE :\t {RMSLE:.4f}')==> 사이킷런 metrics 라이브러리를 활용하여 회귀 평가지표값 구한다.
MAE : 0.5385
MSE : 0.6923
RMSE : 0.8321
MSLE : 0.0296
RMSLE : 0.1721
출처 : 머신러닝·딥러닝 문제해결 전략
(Golden Rabbit , 저자 : 신백균)
※혼자 공부용
'머신러닝 > 캐글_머신러닝_이론' 카테고리의 다른 글
| [PYTHON - 머신러닝_캐글_모델]★선형 회귀 모델★ (0) | 2023.01.31 |
|---|---|
| [PYTHON - 머신러닝_캐글_교차검증]★K-폴드 교차검증★충화 K-폴드 교차검증★folds.split(data)★ (1) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_피처 스케일링]★min-max 정규화★표준화(Standardization) (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_데이터 인코딩]★LabelEncoder★One-Hot-Encoder (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_기본 그래프]★regplot()회귀 선★barplot() vs countplot()★ (0) | 2023.01.31 |
[PYTHON - 머신러닝_캐글_기본 그래프]★regplot()회귀 선★barplot() vs countplot()★
1. titanic 데이터
titanic = sns.load_dataset('titanic')sns.histplot(data= titanic , x='age' ) # 히스토그램은 수치형 데이터의 구간별 빈도수
sns.histplot(data= titanic , x='age' , bins = 10 )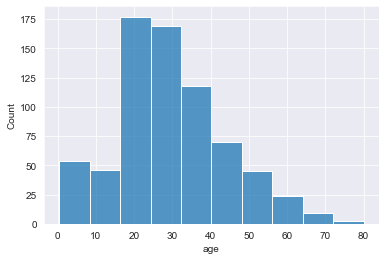
sns.histplot(data= titanic , x='age' , hue = 'alive') # 범주별로 구분 데이터==> hue = 'alive' ==> 범주형 데이터 추가

sns.histplot(data= titanic , x='age' , hue = 'alive' , multiple= 'stack') # 생존자 누적 그래프==> multiple = 'stack' ==> 누적 그래프 출력

sns.kdeplot(data = titanic , x ='age') # 커널밀도추정 함수 그래프(히스토그램을 매끄럽게 곡선으로 연결한 그래프)==> 히스토그램을 곡선으로 연결한 그래프

sns.kdeplot(data = titanic , x ='age' , hue = 'alive' , multiple ='stack') # 누적 커널밀도추정 함수 그래프
sns.displot(data=titanic , x = 'age') # 분포도 : 수치형 데이터 하나의 분포를 나타내는 그래프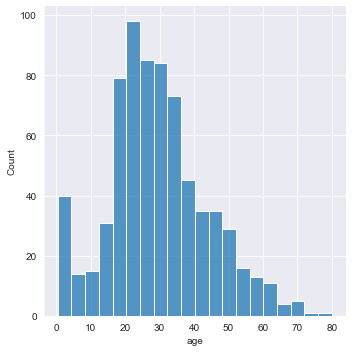
sns.displot(data=titanic , x='age' , kind = 'kde')
sns.kdeplot(data=titanic , x='age')
sns.rugplot(data=titanic , x='age') # 러그플롯은 주변 분포를 나타내는 그래프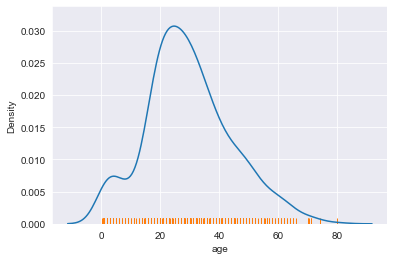
sns.barplot(x='class' , y='fare', data=titanic) # x축에 범주형 데이터, y축에 수치형 데이터==> feature 2개 넣어야한다. x축에 범주형 데이터 , y축에 수치형 데이터

sns.countplot(y='class' , data= titanic)
# barplot은 범주형 데이터 , 수치형 데이터 2개의 피처
# countplot은 범주형 데이터 하나만 받는다.
sns.regplot(x='total_bill' , y ='tip' , data= tips) # regplot()은 선형 회귀선을 동시에 그려주는 함수이다.==> regplot()은 선형 회귀선을 동시에 그려주는 함수

sns.regplot(x='total_bill' , y ='tip' ,ci = 99 , data= tips) # 신뢰구간 99%에 대한 regplot()은 선형 회귀선을 동시에 그려주는 함수이다.
출처 : 머신러닝·딥러닝 문제해결 전략
(Golden Rabbit , 저자 : 신백균)
※혼자 공부용
'머신러닝 > 캐글_머신러닝_이론' 카테고리의 다른 글
| [PYTHON - 머신러닝_캐글_모델]★선형 회귀 모델★ (0) | 2023.01.31 |
|---|---|
| [PYTHON - 머신러닝_캐글_교차검증]★K-폴드 교차검증★충화 K-폴드 교차검증★folds.split(data)★ (1) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_피처 스케일링]★min-max 정규화★표준화(Standardization) (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_데이터 인코딩]★LabelEncoder★One-Hot-Encoder (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_분류와 회귀]★회귀 평가지표★분류 평가지표★ROC, AUC★RMSE (0) | 2023.01.31 |
[PYTHON - 머신러닝_주성분 분석_PCA]★비지도학습★차원 축소★반영 비율 확인
1. PCA(Principal Component Analysis)
==> 비지도 학습 ==> 종속변수는 존재 X ==> 어떤 것을 예측하지도 분류하지도 않는다.
==> 데이터의 차원 축소 : 변수 2개 ==> 2차원 그래프 , 변수 3개 ==> 3차원 그래프 ==> 변수의 개수
==> 변수의 수를 줄여 데이터의 차원을 축소한다. ==> 기존 변수중 일부를 그대로 선택이 아닌, 기존 변수들의 정보를 모두 반영하는 새로운 변수들을 생성
장점 :
㉠ 다차원을 2차원에 적합하도록 차원 축소하여 시각화에 유용하다.
㉡ 변수 간의 높은 상관관계 문제를 해결해준다.
단점 :
㉠ 기존 변수가 아닌 새로운 변수를 사용하여 해석하는 데 어려움이 있다.
㉡ 차원이 축소됨에 따라 정보손실이 일어난다.
2. PCA 실습
from sklearn.decomposition import PCApca = PCA(n_components= 2) # 주성분 개수 지정==> 주성분 개수 지정
pca.fit(customer_X) # 학습
customer_pca = pca.transform(customer_X) # 변환==> 학습 및 변환
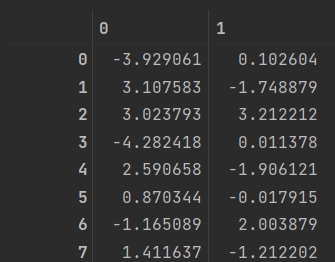
==> 독립변수 여러개가 2차원 으로 축소 되었다.
==> 종속변수(label)
sns.scatterplot(x= 'PC1' , y='PC2' , data = customer_pca , hue = 'label' , palette= 'rainbow') # 산점도 그리기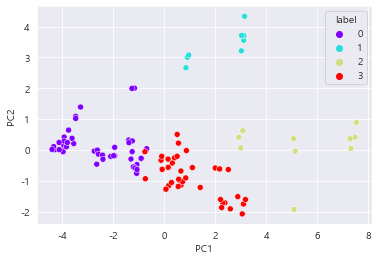
==> 보라색과 빨간색 클러스터는 가깝게 붙어 있어 경계가 모호
==> but. 클러스터들이 얼마나 잘 나뉘었는지를 대략 확인하는 것일 뿐이다.
df_comp = pd.DataFrame(pca.components_, columns = customer_X.columns)
df_comp==> 주성분과 변수의 관계 확인

==> 인덱스 0과 1은 주성분 PC1 과 PC2 의미.
==> 위의 행들은 기존 데이터의 독립변수들
==> 특정 주성분과 특정 변수와의 상관관계
==> ex) PC1 과 amt의 상관관계는 0.35 ==> PC1과 amt는 양의 상관관계
PC2 와 category_gas_transport 의 상관관계는 -0.544==> 음의 상관관계
sns.heatmap(df_comp , cmap='coolwarm')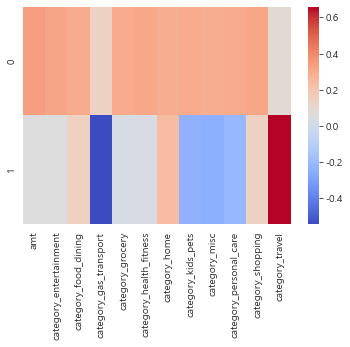
3. PCA 실습-02
from sklearn.model_selection import train_test_split
X_train, X_test , y_train, y_test = train_test_split(data.drop('class' , axis =1) , data['class'] , test_size= 0.2 , random_state= 100)
#학습 셋, 시험 셋 분리from sklearn.preprocessing import StandardScaler
scaler = StandardScaler() # 스케일러 객체 생성
scaler.fit(X_train) # 학습
X_train_scaled = scaler.transform(X_train) # 변환
X_test_scaled = scaler.transform(X_test) # 변환from sklearn.ensemble import RandomForestClassifier
model_1 = RandomForestClassifier(random_state= 100)==> RandomForestClassifier은 ensemble 패키지 안에 있다.
==> 랜덤 포레스트는 매번 다른 방식으로 나무들을 생성한다.
https://knowallworld.tistory.com/376
[PYTHON - 머신러닝_랜덤 포레스트]★str.split(expand= True)★K-폴드 교차검증★하이퍼파라미터 튜닝
1. 랜덤 포레스트 ==> 결정 트리의 단점인 오버피팅 문제를 완화시켜주는 발전된 형태의 트리 모델이다. https://knowallworld.tistory.com/375 [PYTHON - 머신러닝_결정트리]★예측력, 설명력★빈칸 제거_skipin
knowallworld.tistory.com
import time
start_time = time.time() # 시작시간 설정
model_1.fit(X_train_scaled , y_train) # 학습
print(time.time() - start_time) # 소요시간 출력==> 83초
from sklearn.metrics import accuracy_score, roc_auc_score
pred_1 = model_1.predict(X_test_scaled)
accuracy_score(y_test , pred_1)==> 0.958
proba_1 = model_1.predict_proba(X_test_scaled) # 예측 , 소수점 형태로 된 예측값을 사용하기 때문에, predict()가 아닌 predict_proba()를 사용해야 한다.
roc_auc_score(y_test , proba_1[: , 1])https://knowallworld.tistory.com/378
[PYTHON - 머신러닝_LightGBM]★geopy.distance이용한 거리계산★groupby★agg활용한 통계계산★time 라이브
1. LightGBM ==> XGBoost 이후 나온 최신 부스팅 모델. ==> 리프 중심 트리 분할 방식 사용 장점 : ㉠ XGBoost보다 빠르고 높은 정확도를 보여준다. ㉡ 예측에 영향을 미친 변수의 중요도를 확인할 수 있다.
knowallworld.tistory.com
1> pca시 얼마만큼의 데이터 손실이 있는지 파악
pca.explained_variance_ratio_ # 데이터 반영 비율 확인 ==> 기존 데이터의 0.08 정도의 정보만 반영한다.
# ==> 정보의 손실이 크다.0.033314 0.049924 ==> 0.08 정도의 정보만 반영
2> 엘보우기법과 비슷한 주성분 개수 지정
var_ratio = [] # 빈 리스트 생성
for i in range(100, 550 , 50): # 순회
pca = PCA(n_components= i) # 주성분 개수 지정
pca.fit_transform(X_train_scaled)
ratio = pca.explained_variance_ratio_.sum() # 데이터 반영 비율 합
var_ratio.append(ratio)
pca = PCA(n_components= 400 , random_state= 100) # 주성분 개수 지정
pca.fit(X_train_scaled) # 학습
X_train_scaled_pca= pca.transform(X_train_scaled) # 변환
X_test_scaled_pca = pca.transform(X_test_scaled) # 변환
model_2 = RandomForestClassifier(random_state= 100)
start_time = time.time()
model_2.fit(X_train_scaled_pca , y_train)
print(time.time() - start_time)==> 시간이 줄어들었다.
pred_2 = model_2.predict(X_test_scaled_pca) # 예측
accuracy_score(y_test , pred_2) # 정확도 확인==> 정확도도 높아졌다
proba_2 = model_2.predict_proba(X_test_scaled_pca) # 예측
roc_auc_score(y_test , proba_2[:,1])==> AUC도 높아졌다.
출처 : 데싸노트의 실전에서 통하는 머신러닝
(Golden Rabbit , 저자 : 권시현)
※혼자 공부용
'머신러닝 > 머신러닝_이론' 카테고리의 다른 글
| [LogisticRegression()활용] 하이퍼파라미터 값 알아보기★ROC-AUC★L1,L2규제 (0) | 2023.05.27 |
|---|---|
| [머신러닝 이론 01-01] 머신러닝과 통계학 (0) | 2023.03.22 |
| [PYTHON - 머신러닝_결정트리]★예측력, 설명력★빈칸 제거_skipinitialspace★지니 인덱스★오버피팅,언더피팅★트리의 깊이★ (0) | 2023.01.25 |
| [PYTHON - 머신러닝_나이브베이즈]★string.punctuation 특수문자★join함수★nltk.download('stopword')★불용어★ MultinomialNB★오차행렬 (0) | 2023.01.25 |
| [PYTHON - 머신러닝_KNN알고리즘]★value_counts()★고윳값 판단★결측치★스케일링 (0) | 2023.01.24 |
[PYTHON - 머신러닝_K-MEAN 군집화]★엘보우 기법
1.K-MEAN 군집화
==> 비지도 학습의 대표적인 알고리즘 중 하나로 목표 변수가 없는 상태에서 데이터를 비슷한 유형끼리 묶어내는 머신러닝 기법이다.
==> K-최근접 이웃 알고리즘과 비슷하게 거리기반으로 작동하며 적절한 K값을 사용자가 지정해야한다.
==> 거리 기반으로 작동하기 때문에 데이터 위치가 가까운 데이터끼리 한 그룹으로 묶는다.(K 값은 전체 그룹의 수)
클러스터링 : 수많은 데이터를 하나하나 직접 살펴보기보단 적절한 그룹으로 나누고 특징을 살펴볼 수 있다.
장점 :
㉠ 구현이 비교적 간단하다.
㉡ 클러스터링 결과를 쉽게 해석할 수 있다.
단점 :
㉠ 최적의 K값을 자동으로 찾지 못하고, 사용자가 직접 선택해야 한다.
㉡ 거리기반 알고리즘이기 때문에, 변수의 스케일에 따라 다른 결과를 나타낼 수 있다.
유용한곳:
1> 종속변수가 없는 데이터셋에서 데이터 특성을 간단하게 살펴보는 용도
2> 마케팅이나 제품 기획 등을 목적으로 한 고객 분류
3> 지도 학습에서 종속변수를 제외하고 사용 ==> 탐색적 자료 분석 혹은 피처 엔지니어링 용도
2. K-MEAN 모델링
from sklearn.cluster import KMeans
kmeans_model = KMeans(n_clusters= 3 , random_state= 100)
#n_clusters ==> 그룹화 개수
kmeans_model.fit(data) # 학습data['label'] = kmeans_model.predict(data) # 예측
data
sns.scatterplot(x='var_1' , y='var_2' , data=data , hue='label' , palette='rainbow')
#하이퍼파라미터에 hue를 사용해 레이블별로 다른 색상 부여
2. K값 찾기_엘보우 기법
엘보우(elbow method) : 최적의 클러스터 개수를 확인하는 방법
==> 클러스터의 중점과 각 데이터 간의 거리를 기반으로 계산
==> 각 그룹에서의 중심과 각 그룹에 해당하는 데이터 간의 거리에 대한 합을 계산한다. ==> 이너셔 or 관성이라고 한다.
kmeans_model.inertia_ # 이니셔 확인3090.033
==> 이니셔값은 클러스터의 중점과 데이터 간의 거리이므로, 작을수록 그룹별로 오밀조밀 모이게 분류됐다고 할 수 있다.
==> but. 그룹의 개수(K값)이 커지면 당연히 이니셔 값 작아진다. ==> 더 좋아진다고 볼 수 없다.
distance = []
for k in range(2, 10) :
k_model = KMeans(n_clusters=k)
k_model.fit(data) # 학습
distance.append(k_model.inertia_) # 이너셔를 리스트에 저장
distance==> 각 k별 이너셔값 파악
sns.lineplot(x= range(2,10) , y= distance)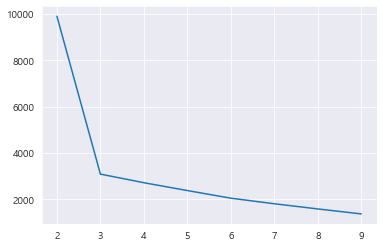
==> 확 꺾어는 x=3 지점을 포착하여 K값으로 내세운다.
3. 전처리 : 피처엔지니어링
customer_dummy = pd.get_dummies(data , columns = ['category']) # 더미 변수로 변환, 모든 범주확인 위해 drop_first= True 하지 않는다.and
customer_dummy.head()from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled_df = pd.DataFrame(scaler.fit_transform(customer_agg) , columns = customer_agg.columns, index = customer_agg.index) # 스케일링 후 데이터프레임으로 변환
scaled_df.head()==> 거리기반 알고리즘 StandardScaler를 사용하여 데이터 스케일러 실행
출처 : 데싸노트의 실전에서 통하는 머신러닝
(Golden Rabbit , 저자 : 권시현)
※혼자 공부용
1. 랜덤 그리드 서치
==> 랜덤 그리드 서치를 활용하여 하이퍼파라미터 튜닝을 진행
==> 기존 그리드 서치와 달리 모든 조합이 아닌 랜덤으로 일부만 선택하여 모델링
https://knowallworld.tistory.com/377
[PYTHON - 머신러닝_XGBoost]★pd.options.display.max_columns★정밀도, 재현율, F1-score
1. 부스팅 알고리즘 ==> 랜덤 포레스트는 각 트리를 독립적으로 만드는 알고리즘 ==> 서로 관련 없이 생성한다. ==> 부스팅은 순차적으로 트리를 만들어 이전 트리로부터 학습한 내용이 다음 트리
knowallworld.tistory.com
※ 그리드 서치
==> 단순작업의 반복 결함 문제 ==> 그리드 서치로 한 번 시도로 수백 가지 하이퍼파라미터 값 시도 가능
==> 그리드 서치에 입력할 하이퍼파라미터 후보들을 입력 ==> 각 조합에 대해 모두 모델링 해보고 최적의 결과가 나오는 하이퍼 파라미터 조합을 알려준다.
from sklearn.model_selection import RandomizedSearchCV
params = {
'n_estimators' : [100, 500 , 1000] , # 반복 횟수
'learning_rate' : [0.01 , 0.05 , 0.1 , 0.3] , # 러닝 메이트
'lambda_l1' : [0 , 10 , 20 , 30 ,50] , # L1 정규화
'lambda_l2' : [0 , 10 , 20 , 30 , 50] , # L2 정규화
'max_depth' : [5 , 10 , 15 , 20] , # 최대 깊이
'subsample' : [0.6 , 0.8 , 1] # 서브샘플 비율
}
피처 셀렉션 : 머신러닝 학습에 사용할 피처를 선택하는 것을 의미
==> 기본적으로 많은 피처(독립변수) 가 있는 것이 풍분한 데이터이기 때문에 머신러닝 학습에 있어서 좋다고 볼 수 있다.
==> 적절하지 못한 피처가 섞인 경우에는 예측결과가 좋지 못할 수 있다. ==> 특정 피처만을 선택하여 모델링했을 때 더 좋은 결과가 나온다.
==> L1 정규화는 피처 셀렉션의 역할을 해주어 불필요한 변수들을 자동으로 학습에서 배제
==> 회귀분석은 모든 피처를 사용하기 때문에 피처 셀렉션을 지원하는 라쏘 회귀, 포워드 셀렉션, 백워드 제거, 재귀적 피처 제거 방법 사용

2. L1 정규화
==> 라쏘 회귀
선형 회귀 모델을 만들면 각 변수에 대한 기울기, 즉 계수가 구해진다. ==> 이 계수에 패널티를 부과하여 너무 큰 계수가 나오지 않도록 강제

==> x는 각 변수에 돌아가는 값이고, w는 해당 변수에 대한 기울기인 계수이다.
==> 각 변수에 들어가는 값과 기울기값을 곱한값 = ^y_i(예측값)
==> L1 정규화는 w에 절대값이 붙어진 채로 더해진다.
==> 큰 기울기값들이 많으면 오차가 더 큰 것으로 간주하여 최적의 모델을 찾을 때 배제된다.
==> 람다는 이 패널티에 대한 가중치를 의미
==> 람다는 우리가 직접 정의할수 있는 하이퍼파라미터 ==> 높은 값을 넣으면 패널티를 더 크게 만들고, 작은 값을 넣으면 패널티의 역할 또한 작아진다.
==> 매개변수에 패널티를 가해서 영향력을 감소시킨다 ==> 오버피팅을 방지하는 목적으로 쓰인다.
==> L1 정규화에서는 람다가 커질 수록 계수가 0이 된다. ==> 변수의 영향력이 사라진다.
==> 불필요한 변수를 제거할 수 있다.
3. L2 정규화
==> 릿지 회귀

==> 추가된 항의 w에 절대값 대신 제곱을 사용하여 기울기의 마이너스 부호를 해결한다
==> L1 정규화와 L2 정규화는 모두 람다값이 커질수록 강한 패널티를 부과하기 때문에 , 크기가 커질수록 변수들에 대한 계수의 절댓값이 작은 모델이 나온다.
==> L2 정규화에서는 람다가 커질 수록 계수의 절대값들이 0에 가깝게 수렴
==> 0에 수렴하여 미미하게나마 변수의 영향력이 존재하여 모든 변수들이 모델에 반영 된다.
4. 랜덤 그리드 서치 모델링
model_2 = lgb.LGBMClassifier(random_state= 100) # 모델 객체 생성
rs = RandomizedSearchCV(model_2 , param_distributions= params , n_iter= 30 , scoring= 'roc_auc' , random_state= 100 , n_jobs= -1) # 랜덤 그리드 서치 객체 생성
#n_iter = 30 ==> 몇 번을 반복할 것인가 ==> 전체 하이퍼파라미터의 조합 중 몇 개를 사용할 것인가import time
start = time.time()
rs.fit(X_train , y_train)
print(time.time())[LightGBM] [Warning] lambda_l1 is set=0, reg_alpha=0.0 will be ignored. Current value: lambda_l1=0
[LightGBM] [Warning] lambda_l2 is set=20, reg_lambda=0.0 will be ignored. Current value: lambda_l2=20
1674798443.4121811
rs.best_params_
==> subsample = 1 ==> 일부가 아닌 전체 사용
=> lambda_l1 : 0 ==> L1 정규화 사용 X
roc_auc_score(y_test , proba_1) # 정확도 확인==> 튜닝 이전 : 0.9366
rs_proba = rs.predict_proba(X_test) # 예측
roc_auc_score(y_test , rs_proba[: , 1]) # 정확도 확인0.9953122884656392
==> AUC 값이 훨씬 높아진 모습을 보인다.
rs_proba_int = (rs_proba[: , 1] > 0.2).astype('int') # 0.2기준으로 분류
print(confusion_matrix(y_test , rs_proba_int)) # 혼동 행렬 확인==> 0.2를 기준으로 0과 1로 분류
[[522519 1130]
[ 504 1508]]
print(classification_report(y_test , rs_proba_int))
정밀도 : 0.62==>0.57==> 감소
재현율 : 0.59==>0.75 ==> 증가
f1-score : 0.61==>0.65 ==> 증가
5. LightGBM의 train() 함수 사용하기
==> XGBoost와 LightGBM에서는 기본적으로 회귀와 분류의 fit() 함수를 사용하여 모델링이 가능하다.
==> train() 함수를 활용하여 모델링 가능하다.
| lgb.train() | lgb.LGBMRegressor.fit() lgb.LGBMClassifier.fit() |
|
| 검증셋 | 모델링 과정에 검증셋 지원 | 모델링에 검증셋 포함 X |
| 데이터셋 | 데이터프레임을 별도의 포맷으로 변환 | 별도의 포맷 필요없이 자동 처리 |
| 하이퍼파라미터 | 무조건 지정 | 기본값으로 모델링 |
| 사이킷런과 연동(그리드 서치, CV) | 불가능 | 가능 |
train = data[data.index < '2020-01-01'] # 훈련셋 설정
val = data[(data.index >= '2020-01-01') & (data.index < '2020-07-01')] # 검증셋 설정
test= data[data.index >= '2020-07-01'] # 시험셋 설정==> val ==> 검증셋
X_train = train.drop('is_fraud' , axis =1 ) # X_train 설정
X_val = val.drop('is_fraud' , axis =1 ) # X_val 설정
X_test= test.drop('is_fraud' ,axis = 1) # X_test 설정
y_train = train['is_fraud'] # y_train 설정
y_val = val['is_fraud'] # y_val 설정
y_test = test['is_fraud'] # y_test 설정d_train = lgb.Dataset(X_train , label=y_train) # 데이터 타입 변환
d_val = lgb.Dataset(X_val , label =y_val) # 데이터 타입 변환
# LightGBM의 Dataset()함수로 LightGBM에서 제시하는 고유한 데이터셋 형태를 취한다.
# 시험셋은 모델링할 때 사용하지 않아 훈련셋과 검증셋에 대해서만 처리해준다.params_set = rs.best_params_ # 최적 파라미터 설정
params_set['metrics'] = 'auc' # 평가 기준 추가
params_set # 하이퍼파라미터 확인
model_3 = lgb.train(params_set , d_train , valid_sets=[d_val] , early_stopping_rounds= 100 , verbose_eval=100) #학습시간 제한 , 출력물은 특정간격으로 보여주기early_stopping_rounds= 100
==> 향후 100개의 트리를 생성하였는데도 개선이 보이지 않는다면 학습을 진행하지 않는다.
verbose_eval=100
==> 100번째, 200번째 , 300번째 의 결과만 보여준다.

pred_3 = model_3.predict(X_test) # 예측==> train()함수로 훈련된 모델은 lgb.LGBMClassifier 의 predict_proba() 역할을 predict()가 대신한다.
roc_auc_score(y_test , pred_3) # 정확도 확인
==> LGBMClassifier/LGBMRegressor 를 사용시 사이킷런의 그리드 서치와 연동되고 데이터 포맷을 변경할 필요가 없어 편리하다.
feature_imp = pd.DataFrame({'feature_name' : X_train.columns , 'importance' : model_1.feature_importances_}).sort_values('importance' , ascending = False) # 중요 변수 정리
plt.figure(figsize=(20, 10))
sns.barplot(x='importance' , y = 'feature_name' , data = feature_imp.head(10))
plt.show()==> feature_importance_

feature_imp_3 = pd.DataFrame(sorted(zip(model_3.feature_importance() , X_train.columns)) , columns = ['Value' , 'Feature']) # 중요 변수 정리
plt.figure(figsize=(20, 10))
sns.barplot(x='importance' , y = 'feature_name' , data = feature_imp.head(10))
plt.show()==> train()함수를 사용하면 검증셋을 활용할 수 있어서 조금 더 신뢰할 만한 결과를 보여준다.
==> feature_importance_

6. 정리
==> LightGBM은 XGBoost와 마찬가지로 트리 기반 모델의 최신 알고리즘.
==> 둘의 가장 큰 차이점은 트리의 가지를 어떤 식으로 뻗어나가는지.
==> XGBoost는 균형 분할 방식으로 각 노드에서 같은 깊이를 형성하도록 한층 한층 밑으로 내려온다.
==> LightGBM은 좌우 노드 수가 균등하지 않고 가지가 깊게 펼쳐진다. ==> 속도가 빠르고, 복잡성은 더 증가하고, 오버피팅 문제를 야기할 가능성이 높다.
==> GPU를 사용한다면 XGBoost가 더 빠른 속도를 보이고, CPU를 사용하면 LightGBM이 더 빠르다.
출처 : 데싸노트의 실전에서 통하는 머신러닝
(Golden Rabbit , 저자 : 권시현)
※혼자 공부용
'머신러닝 > LightGBM' 카테고리의 다른 글
| [LightGBM활용_Kaggle-타이타닉-04] 모델 돌려보기(단독_ Descision Tree) (0) | 2023.05.23 |
|---|---|
| [LightGBM활용_Kaggle-타이타닉-03] 피처별 전처리하기★pd.cut (0) | 2023.05.20 |
| [LightGBM활용_Kaggle-타이타닉-02] 피처별 전처리하기 (1) | 2023.05.20 |
| [LightGBM활용_Kaggle-타이타닉-01] EDA 및 전처리하기 (0) | 2023.05.20 |
| [PYTHON - 머신러닝_LightGBM]★geopy.distance이용한 거리계산★groupby★agg활용한 통계계산★time 라이브러리★민감도, ROC곡선★ (0) | 2023.01.27 |
[PYTHON - 머신러닝_LightGBM]★geopy.distance이용한 거리계산★groupby★agg활용한 통계계산★time 라이브러리★민감도, ROC곡선★
1. LightGBM
==> XGBoost 이후 나온 최신 부스팅 모델. ==> 리프 중심 트리 분할 방식 사용
장점 :
㉠ XGBoost보다 빠르고 높은 정확도를 보여준다.
㉡ 예측에 영향을 미친 변수의 중요도를 확인할 수 있다.
㉢ 변수 종류가 많고 데이터가 클 수록 상대적으로 뛰어난 성능을 보여준다.
단점 :
㉠ 복잡한 모델인 만큼 ,해석에 어려움이 있다.
㉡ 하이퍼파라미터 튜닝이 까다롭다.
유용한 곳:
1> 종속변수가 연속형 데이터인 경우든 범주형 데이터인 경우든 모두 사용 가능
2> 이미지나 자연어가 아닌 표로 정리된 데이터라면 거의 모든 상황에서 활용 가능 ==> XGBoost 와 비슷
2. 데이터 전처리
1> 불필요한 변수들 제외
==> 이상거래(fraud)를 예측 ==> 합리적이지 않다. ==> 이름 관련 변수를 제외가능
2> to_datetime 활용하여 datetime으로 변환
data['trans_date_trans_time'] = pd.to_datetime(data['trans_date_trans_time']) # 날짜 형식으로 변환
data['trans_date_trans_time']
3> 피처엔지니어링
==> 이상거래 감지의 기본적인 아이디어는 해당 고객의 기존 거래 패턴에서 벗어나는 경우를 감지하는 것이다.
ex) 서울에서 카드를 사용하던 사람이 런던에서 고액의 물건을 구매, 주류매장을 이용한 적이 없는데 주류매장에서 고액의 결제
==>Z-점수(Z-score)를 활용하여 패턴 확인
https://knowallworld.tistory.com/220
annotate★IQR★boxplot★z-점수와 분위수★기초통계학-[Chapter03 - 09]
1. z-점수(표준점수_ Standardized score) 산포도 : 자료 중심위치를 나타내는 척도와 밀집 정도 또는 흩어진 정도를 나타낸다. ==> 수능을 치르게 되면 상대적인 위치 관계 이용 ==> ex) 원점수, 표준점수
knowallworld.tistory.com
모집단의 z-점수

표본의 z-점수
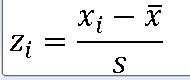
https://knowallworld.tistory.com/253
stats.norm.cdf()★표준정규분포 넓이 구하기!!★ax.lineplot★정규분포(Normal Distribution)★기초통계학-[Ch
1. 정규분포(Normal Distribution) ==> 자료 집단에 대한 도수히스토그램은 자료의 수가 많을 수록 종 모양에 가까운 형태로 나타난다. ==> 종 모양의 확률분포를 정규분포라고 한다. 1>정규분포의 성질
knowallworld.tistory.com

data.groupby('cc_num').count()
==> groupby를 활용하면 count , mean 등 산술연산을 진행해야 한다.
amt_info = data.groupby('cc_num').agg(['mean' , 'std'])['amt'].reset_index() #cc_num별 amt 평균과 표준편차 계산
amt_info.head()==> groupby 활용하여 평균과 표준편차 계산
==> data의 cc_num을 그룹화하고, 평균과 표준편차를 구한다. 그중 amt열만 조사한다.

data = data.merge(amt_info , on = 'cc_num' , how = 'left') # 데이터 합치기
data
data[['amt' , 'mean' , 'std' , 'amt_z_score']].head()
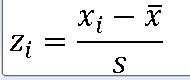
==> 위도 경도 한 변수로 합치기
data['merch_coord'] = pd.Series(zip(data['merch_lat'] , data['merch_long'])) # 위도, 경도 한 변수로 합치기
data['cust_coord'] = pd.Series(zip(data['lat'] , data['long'])) # 위도, 경도 한 변수로 합치기
data

==> zip() 함수를 통하여 괄호로 묶인 위도 경도 값 얻어냈다.
import geopy.distance
data['distance'] = data.apply(lambda x : geopy.distance.distance(x['merch_coord'] , x['cust_coord']).km , axis =1 ) # 거리계산import time
start_time = time.time()
data['distance'] = data.apply(lambda x : geopy.distance.distance(x['merch_coord'] , x['cust_coord']).km , axis =1 ) # 거리계산
end_time = time.time()
print(end_time - start_time)==> time 라이브러리를 활용하여 코드 실행 전과 후의 소요시간 파악 가능하다.

distance_info = data.groupby('cc_num').agg(['mean' , 'std'])['distance'].reset_index() # cc_num 별, 거리 정보 계산
data = data.merge(distance_info , on = 'cc_num' , how = 'left') # 데이터 합치기
data['distance_z_score'] = (data['distance'] - data['mean']) / data['std'] # z-score 계산
data.drop(['mean' , 'std'] , axis =1 , inplace = True) # 변수 제거
data.head()
data['age'] = 2021 - pd.to_datetime(data['dob']).dt.year # dt.year 활요한 나이 계산
data==> dt.year 활용 나이 계산

data = pd.get_dummies(data, columns = ['category' , 'gender'] , drop_first= True)
data
3. 모델링 및 평가하기
==> 신용카드의 이상거래를 감지하여 지금까지 발생한 거래 데이터를 기반으로 모델을 학습 ==> 모델을 이용하여 앞으로 일어나는 거래에 대한 이상 여부 예측
train = data[data.index < '2020-07-01'] # 훈련셋 설정
test = data[data.index >= '2020-07-01'] # 시험셋 설정
len(test) / len(data) # 시험셋 비율 확인 ==> 0.284==> 시험셋 : 0.2 , 훈련셋 : 0.8 ==> 학습시키는데 적당하다.
X_train = train.drop('is_fraud' , axis =1)
X_test = test.drop('is_fraud' , axis = 1)
y_train = train['is_fraud']
y_test = test['is_fraud']import lightgbm as lgb
model_1 = lgb.LGBMClassifier(random_state= 100) # 모델 객체 생성
model_1.fit(X_train , y_train)
pred_1 = model_1.predict(X_test) # 예측==> lightgbm 라이브러리 활용하여 모델 객체 , 학습 및 예측
from sklearn.metrics import accuracy_score , confusion_matrix , classification_report , roc_auc_score
# 정확도 점수 , 혼동 행렬 , 분류 리포트 , ROC AUC 점수
accuracy_score(y_test , pred_1) # 정확도 확인==> 0.99647 ==> 정확도가 약 99.7% ==> but. is_fraud가 0 인경우가 99%이기 때문에 정확도의 의미는 중요치 않다.
print(confusion_matrix(y_test , pred_1)) # 혼동 행렬| 실제값 \ 예측값 | 0 | 1 |
| 0 | 522933 | 716 |
| 1 | 821 | 1191 |
참양성 ==> 1191
거짓양성(1종 오류) ==> 716
거짓음성(2종 오류) ==> 821
print(classification_report(y_test , pred_1)) # 분류 리포트 확인
정밀도 : 0.62
재현율 : 0.59 ==> 실제 이상거래를 얼마나 예측했는지(실제론 정상거래여도 이상거래가 되었는지 여부 예측)를 의미하는 재현율이 이상거래 탐지엔 중요
f1-score : 0.61
정밀도(precision)은 1로 예측한 경우 중, 얼마만큼이 실제로 1인지를 나타낸다.
==> 양성을 양성으로 판단 / (양성을 양성으로 판단 + 1종오류) ==> 1 종오류가 중요하면 정밀도에 주목
재현율(recall)은 실제로 1 중에, 얼마만큼을 1로 예측했는지를 나타낸다.
==> 양성을 양성으로 판단/ (양성을 양성으로판단 + 2종오류) ==> 2 종오류가 중요하면 재현도에 주목
F1-점수(F1-score)은 정밀도와 재현율의 조화평균을 의미한다.
==> 2 * (정밀도 * 재현율) / (정밀도 + 재현율) ==> 1 종오류, 2종오류 중요한 오류가 없다면 F1-SCORE 활용
1> 예측모델의 민감도
pred_1 = model_1.predict(X_test) # 예측
pred_1==> array([0,0,0,0,.....] ) ==> 0.5기준
proba_1 = model_1.predict_proba(X_test) # 예측
proba_1
==> 소수점값 출력으로 모델의 예측값에 대한 민감도를 높였다.
==> 이중 우리가 알고 싶은 값은 1일 가능성 예측 ==> 1 열에만 주목 한다.
proba_1 = proba_1[: ,1] # 1 에 대한 예측 결과 출력
proba_1proba_int1 = (proba_1 > 0.2).astype('int') # 0.2 기준으로 분류
proba_int2 = (proba_1 > 0.8).astype('int') # 0.8 기준으로 분류print(confusion_matrix(y_test , proba_int1))[[522105 1544]
[ 598 1414]]
참양성 ==> 1191 ==> 1414 ==> 증가
거짓양성(1종 오류) ==> 716 ==> 1544 ==> 증가
거짓음성(2종 오류) ==> 821 ==> 598 ==> 감소
print(classification_report(y_test , proba_int1))
정밀도 : 0.62==>0.48 ==> 감소
재현율 : 0.59==>0.70 ==> 증가
f1-score : 0.61==>0.57
print(confusion_matrix(y_test , proba_int2))[[523183 466]
[ 958 1054]]
참양성 ==> 1191 ==> 1054 ==> 감소
거짓양성(1종 오류) ==> 716 ==> 466 ==> 감소
거짓음성(2종 오류) ==> 821 ==> 958 ==> 증가
==> 정상거래를 이상거래로 의심하는 경우는 줄었으나, 이상거래를 놓치는 경우가 많아졌다.
print(classification_report(y_test , proba_int2))
정밀도 : 0.62==>0.69==> 증가
재현율 : 0.59==>0.52 ==> 감소
f1-score : 0.61==>0.60 ==> 감소
2> 예측모델의 민감도
==> 기준점에 따라 재현율이 달라질 수 있어, 최적의 기준점은 모델에 따라 달라진다.
EX) 모델 A에서는 0.4에서 높은 재현율과 적절한 정밀도 얻을 수 있다 ==> 모델 B에서는 0.3이 최적의 기준점이 된다.
==> AUC 활용하여 모호한 모델의 평가 가능
4. AUC(Area Under the ROC Curve)
ROC 곡선 :
민감도(TPR) = TP(참양성) / (TP(참 양성) + FN(거짓 음성) ) = 재현율
==> 실제 1인 것중 얼마만큼 제대로 1로 예측되었는지 ==> 1에 가까울 수록 좋다.
특이도(FPR) = FP(거짓양성) / (FP(거짓 양성) + TN(참 음성) )
==> 실제 0 인 것중 얼마만큼이 1로 잘못 예측되었는지 ==> 0에 가까울 수록 좋다.
ROC 곡선은 ==> X축 FPR , Y축 TPR
AUC (Area Under the ROC Curve) ==> ROC 곡선의 아래쪽에 해당하는 면적
roc_auc_score(y_test , proba_1) # 정확도 확인==> 0.9366009333487075 ==> AUC 또한 정확도와 마찬가지로 종속변수가 한쪽으로 편향될 때 자연스럽게 높게 나오는 경향이 있어 반드시 매우 좋다고 해석 할 수 는 없다.
출처 : 데싸노트의 실전에서 통하는 머신러닝
(Golden Rabbit , 저자 : 권시현)
※혼자 공부용
'머신러닝 > LightGBM' 카테고리의 다른 글
| [LightGBM활용_Kaggle-타이타닉-04] 모델 돌려보기(단독_ Descision Tree) (0) | 2023.05.23 |
|---|---|
| [LightGBM활용_Kaggle-타이타닉-03] 피처별 전처리하기★pd.cut (0) | 2023.05.20 |
| [LightGBM활용_Kaggle-타이타닉-02] 피처별 전처리하기 (1) | 2023.05.20 |
| [LightGBM활용_Kaggle-타이타닉-01] EDA 및 전처리하기 (0) | 2023.05.20 |
| [PYTHON - 머신러닝_LightGBM-02]랜덤 그리드 서치★L1정규화★L2정규화★LGBMClassifer()와 train()의 차이 (0) | 2023.01.27 |