전체 글
-
[PYTHON- 기초통계 -02]★데이터프레임 추출★2023.01.20
[PYTHON - 머신러닝_XGBoost]★pd.options.display.max_columns★정밀도, 재현율, F1-score
1. 부스팅 알고리즘
==> 랜덤 포레스트는 각 트리를 독립적으로 만드는 알고리즘 ==> 서로 관련 없이 생성한다.
==> 부스팅은 순차적으로 트리를 만들어 이전 트리로부터 학습한 내용이 다음 트리를 만들 때 반영한다.
==> 랜덤 포레스트보다 훨씬 빠른 속도와 더 좋은 예측 능력
==> XGBoost , LightGBM , CatBoost 가 있다.
장점 :
㉠ 예측 속도가 빠르고, 예측력이 좋다.
㉡ 변수 종류가 많고 데이터가 클수록 상대적으로 뛰어난 성능을 보인다.
단점 :
㉠ 복잡한 모델인 만큼 , 해석에 어려움이 있다.
㉡ 더 나은 성능을 위한 하이퍼파라미터 튜닝이 까다롭다.
유용한 곳 :
1. 종속변수가 연속형 데이터인 경우, 범주형 데이터인 경우 모두 사용 가능
2. 이미지나 자연어가 아닌 표로 정리된 데이터의 경우
2. 데이터 확인
file_url = "https://media.githubusercontent.com/media/musthave-ML10/data_source/main/dating.csv"
pd.options.display.max_columns = 40
data = pd.read_csv(file_url , skipinitialspace= True) #빈칸 모두 제거
data.head()pd.options.display.max_columns = 40 ==> 볼 수 있는 컬럼의 수 지정
3. 전처리
data.isna().mean() # 결측치 비율 구하기==> 피처 엔지니어링에서 중요도 X 점수로 계산하기 때문에, 중요도와 관련된 변수들은 결측치를 제거하는 방향으로 처리해야한다.
data = data.dropna(subset =['pref_o_attractive' , 'pref_o_sincere' , 'pref_o_intelligence' , 'pref_o_funny' , 'pref_o_ambitious' , 'pref_o_shared_interests',
'attractive_important' , 'sincere_important' , 'intellicence_important' , 'funny_important' , 'ambtition_important' , 'shared_interests_important']) # 일부 변수에서 결측치 제거
data = data.fillna(-99) # 나머지 변수의 결측치는 -99로 대체4. 전처리 : 피처 엔지니어링
==> 데이터에 상대방 나이, 본인 나이가 있어서 , 나이차가 얼마나 나는지 계산 가능.
==> 결측치의 경우 -99를 채워넣었으므로, 단순히 나이차를 계산해서는 안된다.
==> 성별의 경우 단순한 나이 차이보다는 남자가 여자보다 많은지, 반대 경우인지도 고려하는 것이 좋다.
1> 나이 전처리
def age_gap(x):
if x['age'] == -99: # 본인 나이
return -99
elif x['age_o'] == -99: # 상대방 나이
return -99
elif x['gender'] == 'female': # gender가 female이라면
return x['age_o'] - x['age'] # age_o 에서 age를 뺀값 리턴
else:
return x['age'] - x['age_o'] # age에서 age_o를 뺀 값 리턴
# 남녀 중 한명이라도 나이가 -99이면 -99를 반환한다.data['age_gap'] = data.apply(age_gap , axis = 1)
data['age_gap_abs'] = abs(data['age_gap']) # 절댓값 적용
data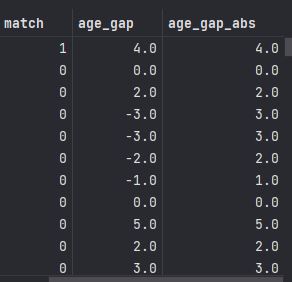
2> 같은 인종 여부
def same_race(x) : # 함수 정의 ==> 인종 데이터 관련 피처 엔지니어링
if x['race'] == -99: # race가 -99 면(결측치 이면)
return -99
elif x['race_o'] == -99 :
return -99
elif x['race'] == x['race_o']: # 인종이 같으면
return 1
else: # 인종이 다르면
return -1data['same_race'] = data.apply(same_race , axis = 1)
data
3> 같은 인종의 중요도 전처리
def same_race_point(x):
if x['same_race'] == -99:
return -99
else:
return x['same_race'] * x['importance_same_race']data['same_race_point'] = data.apply(same_race_point , axis =1)
# data에 same_race_point 함수를 적용한 결과를 same_race_point 변소로 저장
==> 1과 -1로 선정해야 적절한 변별력을 가질 수 있다.
parther_imp = data.columns[8:14] # 상대방 중요도
parttner_rate_me = data.columns[14:20] # 본인에 대한 상대방의 평가
my_imp = data.columns[20:26] # 본인의 중요도
my_rate_partner = data.columns[26:32] # 상대방에 대한 본인의 평가new_label_partner = ['attractive_p' , 'sincere_partner_p' , 'intelligence_p' , 'funny_p' , 'ambition_p' , 'shared_interests_p']
# 상대방 관련 새 변수
new_label_me = ['attractive_m' , 'sincere_partner_m' , 'intelligence_m' , 'funny_m' , 'ambition_m' , 'shared_interests_m']
# 본인 관련 새 변수def rating(data, importance , score) : # 함수 정의
if data[importance] == -99 :
return -99
elif data[score] == -99 :
return -99
else:
return data[importance] * data[score];==> 평가점수 x 중요도 계산 함수
for i,j,k in zip(new_label_partner , partner_imp , partner_rate_me) :
data[i] = data.apply(lambda x : rating(x,j,k) , axis =1 ) # x= 데이터프레임, j = 중요도 변수 이름 , k = 평가 변수
for i,j,k in zip(new_label_me, my_imp , my_rate_partner):
data[i] = data.apply(lambda x : rating(x,j,k) , axis =1 )data = pd.get_dummies(data , columns = ['gender' , 'race' , 'race_o'] , drop_first= True) # 더미 변수로 변환
data==> object 타입 변수들은 문자 형태이기 때문에, 숫자 형태가 되게끔 더미변수로 전환
https://knowallworld.tistory.com/372
[PYTHON - 머신러닝_로지스틱선형회귀]★로지스틱 선형회귀★상관관계★원-핫 인코딩★정확도★
1. 로지스틱 회귀 ==> 로지스틱 회귀 또한 선형 회귀처럼 기본 분석 모델이다. ==>선형 회귀 분석은 연속된 변수를 예측하는 반면 , 로지스틱 회귀 분석은 Yes/No처럼 2가지로 나뉘는 분류 문제를 다
knowallworld.tistory.com
==>파이썬은 자료형이 object인 변수들 , 데이터가 숫자가 아닌 문자인 변수를 이해 못한다.
EX) object형을 숫자로 대체하는 방법, 계절의 경우 봄,여름,가을,겨울을 각각 1,2,3,4로 변환
5. 모델링 및 평가
from sklearn.model_selection import train_test_split
X_train , X_test , y_train , y_test = train_test_split(data.drop('match', axis =1) , data['match'] , test_size= 0.2 , random_state= 100) # 훈련셋/ 시험셋 분리==> 훈련 셋 , 시험셋 분리
import xgboost as xgb
model = xgb.XGBClassifier(n_estimators = 500 , max_depth = 5 , random_state = 100) # 모델 객체 생성
model.fit(X_train , y_train) # 훈련
pred = model.predict(X_test) # 예측
from sklearn.metrics import accuracy_score , confusion_matrix , classification_report
accuracy_score(y_test , pred) # 정확도==> 독립변수 훈련 셋 X_train , 종속변수 훈련 셋 y_train으로 훈련
==> 독립변수 훈련 셋으로 예측 진행
==> 정확도는 (종속변수 시험셋, 예측값과의 차이) 를 이용하여 계산
==> 0.8616236162361623
==> 86% 정확도 ==> 종속변수 match의 평균값은 0.164이다.
==> 매칭된 경우가 16% 정도라는 것이다. 나머지 84%는 매칭되지 않았다.
==> 모델링 없이 모든 경우를 0으로만 예측해도 84%는 맞출 수 있다.
https://knowallworld.tistory.com/374
[PYTHON - 머신러닝_나이브베이즈]★string.punctuation 특수문자★join함수★nltk.download('stopword')★불용
1. 나이브 베이즈 ==> 조건부 확률 기반의 분류 모델 https://knowallworld.tistory.com/232 ★Multi Indexing★곱의 법칙★조건부 확률★기초통계학-[Chapter04 - 확률-04] 1. 조건부확률(Conditional Probability) ==> 0보다
knowallworld.tistory.com
==> confusion_matrix() ==> 혼동(오차) 행렬 ==> 제 1종오류 , 제 2종오류 출력 가능
[[1291 74]
[ 151 110]]
| 실제값 \ 예측값 | 0 | 1 |
| 0 | 1291 | 74 |
| 1 | 151 | 110 |
==> 실제로 매칭이 안되었는데, 실제로 매칭이 안되었다고 예측한 경우 : 1291 건
==> 실제로 매칭이 되었는데, 실제로 매칭되었다고 예측한경우 : 110 건
==> 실제로 매칭이 안되었는데, 매칭이 되었다고 예측한 경우 : 74 건(제 1종 오류)
==> 실제로 매칭이 되었는데 , 매칭이 안되었다고 예측한 경우 : 151 건 (제 2종 오류)
==> 모델 간의 비교/평가를 진행할 때는 오류 유형에 따른 평가를 해야한다.
print(classification_report(y_test , pred))
precision recall f1-score support
0 0.90 0.95 0.92 1365
1 0.60 0.42 0.49 261
accuracy 0.86 1626
macro avg 0.75 0.68 0.71 1626
weighted avg 0.85 0.86 0.85 1626
==> 정밀도, 재현율 , F1-점수 , 인덱스에 해당하는 개수
==> 예측하려는 값 1에 대한 해석
정밀도(precision)은 1로 예측한 경우 중, 얼마만큼이 실제로 1인지를 나타낸다.
==> 양성을 양성으로 판단 / (양성을 양성으로 판단 + 1종오류) ==> 1 종오류가 중요하면 정밀도에 주목
재현율(recall)은 실제로 1 중에, 얼마만큼을 1로 예측했는지를 나타낸다.
==> 양성을 양성으로 판단/ (양성을 양성으로판단 + 2종오류) ==> 2 종오류가 중요하면 재현도에 주목
F1-점수(F1-score)은 정밀도와 재현율의 조화평균을 의미한다.
==> 2 * (정밀도 * 재현율) / (정밀도 + 재현율) ==> 1 종오류, 2종오류 중요한 오류가 없다면 F1-SCORE 활용
※ 조화평균 : 주어진 수들의 역수의 산술평균의 역수
H = 2 * a_1 * a_2 / (a_1 + a_2)
※ 산술평균 : 주어진 수의 합을 수의 개수로 나눈 값
A = (a_1 + a_2) / 2
6. 그리드 서치 : 하이퍼파라미터 튜닝
==> 이전의 하이퍼파라미터 뉴닝은 임의 값들을 넣어 더 나은 결과를 찾는 방식
==> 단순작업의 반복 결함 문제 ==> 그리드 서치로 한 번 시도로 수백 가지 하이퍼파라미터 값 시도 가능
==> 그리드 서치에 입력할 하이퍼파라미터 후보들을 입력 ==> 각 조합에 대해 모두 모델링 해보고 최적의 결과가 나오는 하이퍼 파라미터 조합을 알려준다.
max_depth = [3,5,10]
learning_rate = [0.01, 0.05 , 0.1]
#==> 그리드 서치 적용시 9가지 조합 생성
# 9가지 조합을 각각 모델링 ==> 그리드 서치에서는 교차검증도 함께 사용 ==> 교차검증의 횟수만큼 곱해진 횟수가 모델링==> K-폴드값을 5로 교차검증한다면 9*5 = 45회의 모델링 진행
https://knowallworld.tistory.com/376
[PYTHON - 머신러닝_랜덤 포레스트]★str.split(expand= True)★K-폴드 교차검증★하이퍼파라미터 튜닝
1. 랜덤 포레스트 ==> 결정 트리의 단점인 오버피팅 문제를 완화시켜주는 발전된 형태의 트리 모델이다. https://knowallworld.tistory.com/375 [PYTHON - 머신러닝_결정트리]★예측력, 설명력★빈칸 제거_skipin
knowallworld.tistory.com
데이터를 특정 개수(K개) 로 쪼개어서 그중 하나씩을 선택하여 시험셋으로 사용하되, 이 과정을 K번만큼 반복
from sklearn.model_selection import GridSearchCV #import
parameters = {
'learning_rate' : [0.01 , 0.1 , 0.3] ,
'max_depth' : [5 , 7 , 10] ,
'subsample' : [0.5 , 0.7 , 1] ,
'n_estimators' : [300, 500 , 1000]
} # 하이퍼파라미터 셋 정의
1> learning_rate : 경사하강법에서 '매개변수'를 얼만큼씩 이동해가면서 최소 오차를 찾을지, 그 보폭의 크기를 결정하는 하이퍼파라미터
==> 보폭은 미분계수에 의해 결정된다. ==> 학습률이라고도 한다.
==> 너무 작은 학습률(보폭)을 가지면 최소 에러값을 찾는데 상당한 시간이 들고, 지역 최소해에 빠질 가능성이 있다.
==> 너무 큰 학습률(보폭)을 가지면, 최소 에러를 정확히 찾지 못하고 좌우로 계속 넘어다닌다.
2> max_depth : 각 트리의 깊이 제한
3> subsample : 모델을 학습시킬 때 일부 데이터만 사용하여 각 트리 생성. 0.5를 쓰면 데이터의 절반씩만 랜덤 추출하여 트리 생성
4>n_estimators : 전체 나무의 개수
gs_model = GridSearchCV(model , parameters ,n_jobs=-1 , scoring='f1' , cv = 5) # n_jobs 는 사용할 코어 수 , scoring은 모델링할때 어떤 기준으로 최적의 모델을 평가할지, cv는 K-FOLD 값gs_model.fit(X_train , y_train) # 학습==> 하이퍼파라미터셋이 총 4종류 , 3개씩 값이 있으므로 , 3**4 = 81번의 모델링
==> 교차검증 5회 ==> 81 * 5 = 405번의 모델링 작업 ==> 소요시간이 길다.
gs_model.best_params_ # 최적의 하이퍼파라미터 출력==> 최적의 파라미터 출력
==> {'learning_rate': 0.300,
'max_depth': 5,
'n_estimators': 1000,
'subsample': 0.500}
pred = gs_model.predict(X_test)==> 예측값 생성
accuracy_score(y_test , pred)==> 0.8610086100861009 => 정확도 계산
print(classification_report(y_test , pred)) precision recall f1-score support
0 0.90 0.94 0.92 1365
1 0.59 0.44 0.50 261
accuracy 0.86 1626
macro avg 0.74 0.69 0.71 1626
weighted avg 0.85 0.86 0.85 1626
==> 이전에 비해 정확도는 미세하게 올라갔고, F1-점수는 0.02 상승했다.
==> 하이퍼파라미터 튜닝으로 엄청난 개선을 얻기는 힘들다. 예측에는 피처 엔지니어링과 모델 알고리즘 선정이 큰 영향을 미친다. 하이퍼파라미터 튜닝은 조금이라도 더 나은 모델을 만드는 역할이다.
7. 중요 변수 확인
==> 선형 회귀와 로지스틱 회귀에서는 계수로, 결정 트리에서는 노드의 순서로 변수의 영향력을 확인했다.
==> XGBoost에 내장된 함수는 변수의 중요도 까지 계산해준다.
==> 그리드 서치로 학습된 모델에서는 이 기능을 사용할 수 없다. ==> 그리드 서치에서 찾은 최적의 하이퍼파라미터 매개변수 조합으로 다시 한번 학습시킨다.
model = xgb.XGBClassifier(learning_rate = 0.3 , max_depth = 5 , n_estimators = 1000 , subsample = 0.5 , random_state = 100)
model.fit(X_train , y_train)model.feature_importances_ # 변수 중요도 확인
feature_imp = pd.DataFrame({'features' : X_train.columns , 'values' : model.feature_importances_}) #데이터프레임으로 전환
feature_imp
plt.figure(figsize = (20 , 10))
sns.barplot(x='values' , y='features' , data = feature_imp.sort_values(by = 'values' , ascending=False).head(10))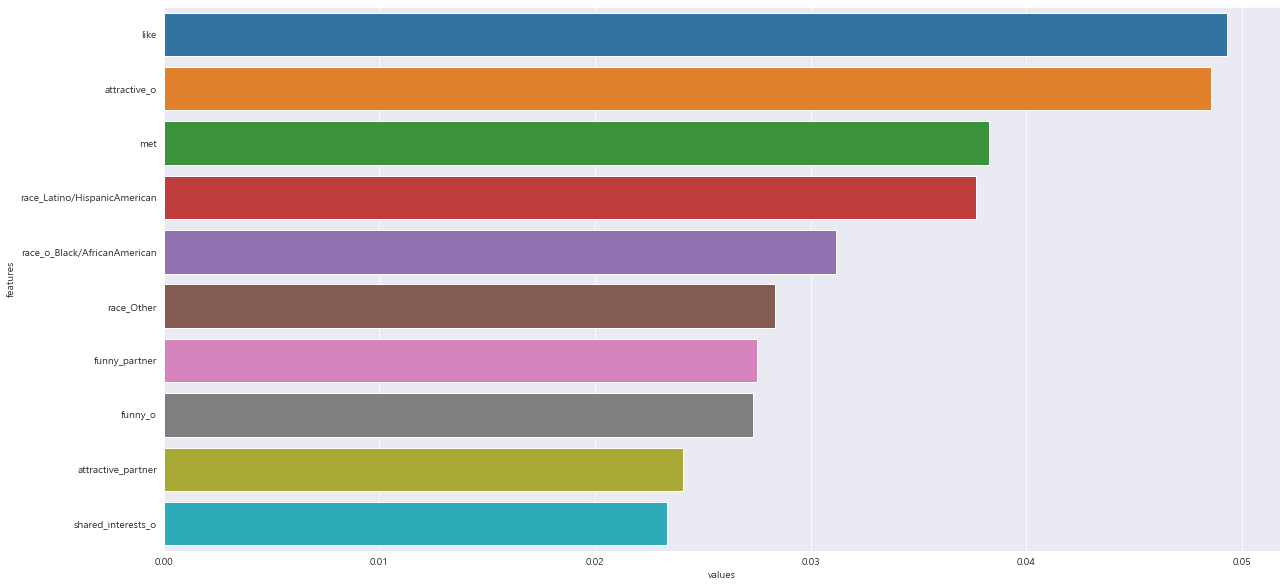
출처 : 데싸노트의 실전에서 통하는 머신러닝
(Golden Rabbit , 저자 : 권시현)
※혼자 공부용
[PYTHON - 머신러닝_랜덤 포레스트]★str.split(expand= True)★K-폴드 교차검증★하이퍼파라미터 튜닝
1. 랜덤 포레스트
==> 결정 트리의 단점인 오버피팅 문제를 완화시켜주는 발전된 형태의 트리 모델이다.
https://knowallworld.tistory.com/375
[PYTHON - 머신러닝_결정트리]★예측력, 설명력★빈칸 제거_skipinitialspace★지니 인덱스★오버피팅,
1. 결정 트리(Decision Tree) ==> 관측값과 목표값을 연결시켜주는 예측 모델로서 나무 모양으로 데이터를 분류 ==> 수많은 트리 기반 모델의 기본 모델 ==> 선형 모델은 각 변수에 대한 기울기값들을
knowallworld.tistory.com
오버피팅 : 예측 모델이 훈련 셋을 지나치게 잘 예측한다면 새로운 데이터를 예측 할 때 큰 오차를 유발 할 수 있다. ==> 훈련 셋과 테스트 셋의 예측 정확도를 줄여야 한다.
==> 랜덤으로 생성된 무수히 많은 트리를 이용하여 예측
==> 여러 모델을 활용하여 하나의 모델을 이루는 기법을 앙상블이라 부른다.
==> 앙상블 기법 : 여러 모델을 만들고 각 예측값을 투표/평균 등으로 통합하여 더 정확한 예측 도모
장점 :
㉠ 결정 트리와 마찬가지로, 아웃라이어에 거의 영향을 받지 않는다.
㉡ 선형/비선형 데이터에 상관없이 잘 작동한다.
단점 :
㉠ 학습 속도가 상대적으로 느리다.
㉡ 수많은 트리를 동원하기 때문에 모델에 대한 해석이 어렵다.
2. 변수 전처리
data['engine']
data['engine'].str.split(expand = True) # 컬럼 하나씩만 인덱싱 해준다.
# 공백 기준으로 문자를 분할하여 별도의 변수로 출력==> expand = True ==> 2개의 컬럼으로 나눈다.

data[['engine' , 'engine_unit']] = data['engine'].str.split(expand = True)
# 분할된 문자들을 새로운 변수들로 저장
data['engine'].head()==> 'engine' 열 , 'engine_unit' 열 생성
def isFloat(value): # 함수 정의
try : # 시도
num = float(value) # 값을 숫자로 변환
return num # 변환된 값 리턴
except ValueError: # try에서 ValueError가 난 경우
return np.NaN # np.NaN 리턴==> 에러가 발생했던 'bhp' 는 숫자로 변환할 수 없으므로 except 블록으로 넘어간다.
==> except Valuerror인 경우 NaN 값으로 대체한다.
def mile(x) :
if x['fuel'] == 'Petrol':
return x['mileage'] / 80.43
elif x['fuel'] == 'Diesel':
return x['mileage'] / 73.56
elif x['fuel'] == 'LG':
return x['mileage'] / 40.85
elif x['fuel'] == 'CNG':
return x['mileage'] / 44.23data['mileage'] = data.apply(mile , axis=1) # mile 함수로 마일리지 수정
data[['fuel' ,'mileage']]
def torque_unit(x):
if 'NM' in str(x):
return 'NM'
elif 'KGM' in str(x):
return 'kgm'
data['torque_unit'] = data['torque'].apply(torque_unit)
data[['torque' , 'torque_unit']]
data['torque_unit'].isna()
data[data['torque_unit'].isna()]
data[data['torque_unit'].isna()]['torque'].unique() #==> torque_unit이 NULL 값인 행의 'torque' 열의 고윳값 출력
def split_num(x):
x = str(x)
for i,j in enumerate(x):
if j not in '0123456789.' : # 만약 j가 0123456789.에 포함되지 않으면
cut= i
break
return x[:cut]==> x = str(x) ==> string 화
data['torque'] = data['torque'].apply(split_num)
data['torque']
data['torque'] = data['torque'].replace('' , np.NaN)==> 빈칸 값을 ==> NaN 값으로 대체하기
data['torque'] = data['torque'].astype('float64')==> 'float64'로 변환하기
def torque_trans(x) :
if x['torque_unit'] == 'kgm':
return x['torque'] * 9.8066
else:
return x['torque']
data['torque'] = data.apply(torque_trans , axis =1 ) #함수 적용
data['torque']==> 단위에 따른 차이를 맞춰주는 변환
3. 결측치 처리와 더미변수화
data.dropna(inplace = True) #결측치 행 제거==> 결측치 행 제거
data = pd.get_dummies(data , columns = ['name' , 'fuel' , 'seller_type' , 'transmission' , 'owner'], drop_first= True)
data
==> 더미 변수화
4. 모델링 및 평가하기
from sklearn.model_selection import train_test_split
X_train , X_test, y_train , y_test = train_test_split(data.drop('selling_price' , axis =1 ) , data['selling_price'] , test_size= 0.2 ,random_state=100)
# 훈련 셋/ 시험 셋 분리from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier(random_state= 100)
model.fit(X_train , y_train)
train_pred = model.predict(X_train)
test_pred = model.predict(X_test)==> 랜덤 포레스트 모델은 사이킷런의 ensemble 패키지 안에 속해 있다.
==> 랜덤 포레스트는 매번 다른 방식으로 나무들을 생성하므로, random_state를 지정한다.
==> 훈련 셋으로 학습한 훈련셋과 시험셋에 대한 예측값 2가지를 모두 구한다.
from sklearn.metrics import mean_squared_error #RMSE 이용
print('train_rmse : ' , mean_squared_error(y_train , train_pred)**0.5 , 'test_rmse : ' , mean_squared_error(y_test , test_pred) **0.5)5. K-폴드 교차검증
==> 교차검증의 목적은 모델의 예측력을 더 안정적으로 평가하기 위함이다.
==> 새로운 데이터를 얼마나 잘 예측하는지 확인하고자 훈련셋과 시험셋을 나누어서 평가하였다.
==> 데이터 분할은 랜덤 샘플링으로 이루어졌기 때문에 안정적이다.
==> BUT. 우연한 오차들이 예측력을 평가하는 데 작은 노이즈로 존재한다.
==> random_state 매개변수에 다양한 숫자를 넣어보면 매번 훈련셋의 평가값(RMSE, accuracy score)가 계속 변한다.
==> 작은 오차들 고려하여 평가하는 방법이 교차검증
==> 더 낮은 RMSE를 얻기 위함이 아니라, 우연의 요소가 배제된 더 신뢰할 만한 결과를 얻기 위함이다.
1> K-폴드 교차검증 :
데이터를 특정 개수(K개) 로 쪼개어서 그중 하나씩을 선택하여 시험셋으로 사용하되, 이 과정을 K번만큼 반복
이터레이션 1
| 훈련 셋 | 훈련 셋 | 훈련 셋 | 훈련 셋 | 시험 셋 |
이터레이션 2
| 훈련 셋 | 훈련 셋 | 훈련 셋 | 시험 셋 | 훈련 셋 |
이터레이션 3
| 훈련 셋 | 훈련 셋 | 시험 셋 | 훈련 셋 | 훈련 셋 |
이터레이션 4
| 훈련 셋 | 시험 셋 | 훈련 셋 | 훈련 셋 | 훈련 셋 |
이터레이션 5
| 시험 셋 | 훈련 셋 | 훈련 셋 | 훈련 셋 | 훈련 셋 |
==> 이터레이션(반복)은 모델링을 수행하는 단위 이다.
==> 이터레이션의 평가값(오차)의 평균값을 내어 RMSE를 도출한다.
2> 코드
from sklearn.model_selection import KFold
data.reset_index(drop=True , inplace =True) # drop 매개변수를 사용하지 않으면 기존 인덱스가 새로운 컬럼 형태로 추가된다.==> data 결측치 행 제거하였으므로 , index값 초기화 시켜준다. drop = True로 index 열 생성 방지
kf = KFold(n_splits=5) #KFold 객체 생성 , 5개로 분할
X = data.drop('selling_price' , axis =1 ) # 종속변수 제거하여 X에 저장
y = data['selling_price'] # 종속변수를 y에 저장for i, j in kf.split(X) : # 순회
print(i , j )[1575 1576 1577 ... 7868 7869 7870] [ 0 1 2 ... 1572 1573 1574]
[ 0 1 2 ... 7868 7869 7870] [1575 1576 1577 ... 3146 3147 3148]
[ 0 1 2 ... 7868 7869 7870] [3149 3150 3151 ... 4720 4721 4722]
[ 0 1 2 ... 7868 7869 7870] [4723 4724 4725 ... 6294 6295 6296]
[ 0 1 2 ... 6294 6295 6296] [6297 6298 6299 ... 7868 7869 7870]
==> 훈련 셋과 시험셋으로 사용할 인덱스 출력 ==> 5개의 다른 공간 보여준다.
from sklearn.ensemble import RandomForestRegressor
train_rmse_total = []
test_rmse_total = []
for train_index , test_index in kf.split(X):
X_train , X_test = X.loc[train_index] , X.loc[test_index]
y_train , y_test = y[train_index] , y[test_index]
model = RandomForestRegressor(random_state= 100) # 모델 객체 생성
model.fit(X_train , y_train) # 학습
train_pred = model.predict(X_train) # 훈련셋 예측
test_pred = model.predict(X_test) # 시험셋 예측
train_rmse = mean_squared_error(y_train , train_pred) **0.5 # 훈련 셋 rmse 계산
test_rmse = mean_squared_error(y_test , test_pred) **0.5 # 시험 셋 rmse 계산
train_rmse_total.append(train_rmse)
test_rmse_total.append(test_rmse)==> X_train , X_test , y_train , y_test 정의 하여 mean_squared_error 활용하여 RMSE 값 도출한다.
print('train_rmse : ' , sum(train_rmse_total)/5 , 'test_rmse :' , sum(test_rmse_total)/5)==> 최종 RMSE는 오차값들의 평균이다. ==> 5를 나누어 준다.
6. 랜덤 포레스트
==> 랜덤 포레스트는 결정 트리의 집합체
==> 결정트리만 사용하면 오버피팅의 문제가 생긴다. ==> 랜덤 포레스트가 여러개의 트리를 만들 때는 데이터 전체가 아닌 매번 다른 일부의 데이터를 사용하여 다른 트리를 만들어낸다.
==> 전체 데이터를 사용한 결과보다 예측력이 떨어질 수 있으나, 예측력이 떨어지는 수많은 트리들과 함께 중위값을 찾아내면 오버피팅을 막는 데 효율적이다.
일부 데이터를 취하는 기준
1> 데이터의 행(row) 기준으로 일부씩만 추출 ==> 1만 행의 데이터가 있다고 할때 , 1 만행 전체를 사용하는 게 아닌 약 2/3에 해당하는 데이터만을 사용 ==> 다른 결과의 트리 생성
2> 데이터의 열(column) 변수 기준 ==> A라는 변수가 예측하는데 결정적인 역할을 한다고 가정, 트리 1000개를 만들더라도 최상위 노드에서의 분류 기준은 항상 A 변수가 된다.
==> 다른 변수들에게 가중치 부여하여 오버피팅을 피하도록 한다.
==> 랜덤포레스트의 최종 예측값은 각 트리의 예측값들을 기반으로 만들어진다. ==> 회귀 문제는 연속형 변수를 예측하기 때문에, 각 트리에서 만들어낸 예측값들의 평균값을 랜덤 포레스트의 최종 예측값으로 사용한다.
==> 분류 문제는 각 트리에서 예측한 값들 중 최다 투푯값으로 랜덤 포레스트의 예측값이 결정된다.
==> EX) 0과 1을 분류하는 문제에서 총 1000개 트리 중 700개 트리가 1로 예측하고 300개 트리가 0으로 예측했다면, 가장 많은 투표를 받은 1이 랜덤 포레스트의 최종 예측값이 된다.
7. 하이퍼파라미터 튜닝
==> 랜덤 포레스트는 수많은 하이퍼파라미터를 갖고 있다.
n_estimators : 랜덤 포레스트를 구성하는 결정 트리의 개수
max_depth : 결정 트리와 동일하게, 각 트리의 최대 깊이를 제한
min_samples_split : 해당 노드를 나눌 것인지 말 것인지를 노드 데이터 수를 기준으로 판단한다. ==> 이 매개변수에 지정된 숫자보다 적은 수의 데이터가 노드에 있으면 더는 분류하지 않는다.
min_samples_leaf : 분리된 노드의 데이터에 최소 몇 개의 데이터가 있어야 할지를 결정하는 매개변수이다. ==> 이 매개변수에 지정된 숫자보다 적은 수의 데이터가 분류된다면, 해당 분리는 이루어지지 않는다.
n_jobs : 병렬 처리에 사용되는 CPU 코어 수. 많은 코어를 사용할수록 속도는 빨라지며, -1을 입력하면 지원하는 모든 코어를 사용한다.
from sklearn.ensemble import RandomForestRegressor
train_rmse_total = []
test_rmse_total = []
for train_index , test_index in kf.split(X):
X_train , X_test = X.loc[train_index] , X.loc[test_index]
y_train , y_test = y[train_index] , y[test_index]
model = RandomForestRegressor(n_estimators= 300 , max_depth= 50 , min_samples_split=5 , min_samples_leaf= 1 , n_jobs= -1 , random_state= 100) # 모델 객체 생성
model.fit(X_train , y_train) # 학습
train_pred = model.predict(X_train) # 훈련셋 예측
test_pred = model.predict(X_test) # 시험셋 예측
train_rmse = mean_squared_error(y_train , train_pred) **0.5 # 훈련 셋 rmse 계산
test_rmse = mean_squared_error(y_test , test_pred) **0.5 # 시험 셋 rmse 계산
train_rmse_total.append(train_rmse)
test_rmse_total.append(test_rmse)==> 오버피팅이 줄어들었다.
8. 정리
1> 중고차의 가격을 예측하는 모델 만들기
2> pandas, numpy , matplotlib , seaborn 라이브러를 임포트하여 데이터 처리하기
3> 텍스트 데이터, 결측치 처리와 더미 변수를 변환한다.
4> RandomForest를 사용하여 예측 모델을 만들었다. 연속형 변수이기 때문에 RMSE를 좋다/나쁘다로 평가할 수는 없다.
5> RandomForest에서 쓸수 있는 몇가지 하이퍼파라미터를 변경하여 test_rmse(평균 제곱근 편차)를 조금 낮출 수 있었다.
출처 : 데싸노트의 실전에서 통하는 머신러닝
(Golden Rabbit , 저자 : 권시현)
※혼자 공부용
1. 결정 트리(Decision Tree)
==> 관측값과 목표값을 연결시켜주는 예측 모델로서 나무 모양으로 데이터를 분류
==> 수많은 트리 기반 모델의 기본 모델
==> 선형 모델은 각 변수에 대한 기울기값들을 최적화하여 모델을 만들어 나감.
==> 트리모델에서는 각 변수의 특정 지점을 기준으로 데이터를 분류해가면서 예측모델 만든다.
예측력 : 모델 학습을 통해 얼마나 좋은 예측치를 보여주는가를 의미
설명력 : 학습된 모델을 얼마나 쉽게 해석할 수 있는지를 뜻한다.
==> 알고리즘의 복잡도가 증가할 수록 예측도는 증가 , 설명력은 감소
ex) 의학 데이터에 대한 질병 발병률에 대한 예측 모델 ==> 설명력이 좋은 알고리즘이 적합
장점 :
㉠ 데이터에 대한 가정이 없는 모델이다. 선형 모델은 정규분포에 대한 가정이나 독립변수와 종속변수의 선형 관계 등을 가정으로 하는 모델이지만, 결정 트리는 데이터에 대한 가정이 없어서 자유롭게 적용할 수 있다.
㉡ 아웃라이어에 영향을 거의 받지 않는다.
㉢ 트리 그래프를 통해서 직관적으로 이해하고 설명할 수 있다.
단점 :
㉠ 트리 기반 모델들에 비하면 예측력이 떨어진다.
2. 데이터 확인
file_url = "https://media.githubusercontent.com/media/musthave-ML10/data_source/main/salary.csv"
data = pd.read_csv(file_url , skipinitialspace= True) #빈칸 모두 제거
data.head()==> skipinitialspace =True ==> 앞에 있는 빈칸 제거하여 갖고오기
data.describe(include= 'all') #object형이 포함된 통계정보 출력==> object형이 포함된 통게정보 출력

==> unique, top , freq 행이 추가되었다. ==> 오직 object형의 변수들만을 위한 것이다. 기존의 숫자형 변수들은 NaN으로 처리되어 있다.
unique : 고윳값
top : 각 변수별로 가장 많이 등장하는 value
freq : top에 나와있는 value가 해당 변수에서 총 몇 건인지
3. 전처리 : 범주형 데이터
data['class'] = data['class'].map({'<=50K' : 0 , '>50K' : 1}) # 숫자로 변환obj_list = []
for i in data.columns : #순회
if data[i].dtype == 'object' : #데이터타입이 object이면
obj_list.append(i) #리스트에 변수 이름을 추가
obj_list==> data type이 object 인거 obj_list에 추가
['workclass',
'education',
'marital-status',
'occupation',
'relationship',
'race',
'sex',
'native-country']
for i in obj_list:
if data[i].nunique() >= 10: #변수의 고윳값이 10보다 크거나 같으면
print(i , data[i].nunique()) #컬럼명과 고윳값 개수 출력education 16
occupation 14
native-country 41
np.sort(data['education-num'].unique()) #고윳값을 오름차순으로 확인data[data['education-num'] == 1] # 값이 1인 (True)행만 필터링
data[data['education-num'] == 1]['education'].unique()
#education-num이 1인 데이터들의 education 고윳값 확인
array([ 'Preschool'] , dtype = object)
for i in np.sort(data['education-num'].unique()):
print(i, data[data['education-num'] ==i]['education'].unique() )==> education-num이 고윳값별 education의 고윳값 확인
1 [' Preschool']
2 [' 1st-4th']
3 [' 5th-6th']
4 [' 7th-8th']
5 [' 9th']
6 [' 10th']
7 [' 11th']
8 [' 12th']
9 [' HS-grad']
10 [' Some-college']
11 [' Assoc-voc']
12 [' Assoc-acdm']
13 [' Bachelors']
14 [' Masters']
15 [' Prof-school']
16 [' Doctorate']
data.groupby('native-country').mean().sort_values('class')==> 그룹별 평균 계산 후 class 기준으로 오름차순 정렬
※ 더미 변수를 설명할 때, 범주형 데이터를 무작정 숫자로 치환하여 모델링하는 방법은 좋지 않다.
but. 트리 기반의 모델을 사용 할 때 연속된 숫자들도 연속적으로 받아들이기 보다는 일정 구간을 나누어 받아들인다.
==> 트리가 충분히 깊어지면 범주형 변수를 숫자로 바꾼다고 해도 문제가 없다.
country_group = data.groupby('native-country').mean()['class']
country_group= country_group.reset_index() #인덱스를 변수로 불러냄
country_group
4. 결측치 처리 및 더미 변수 변환
data.isna().mean() #결측치 비율 확인
data['native-country'] = data['native-country'].fillna(-99)
# native-country의 경우 각 국가별 class의 평균값으로 대체한 상황
# 트리 기반 모델에서는 결측치를 임의의 숫자로 채워도 괜찮다.native-country의 경우 각 국가별 class의 평균값으로 대체한 상황 ==> 트리 기반 모델에서는 결측치를 임의의 숫자로 채워도 괜찮다.
data['workclass'] = data['workclass'].fillna('Private')
# 결측치를 Private(특정 값이 대부분을 차지하는 경우라면 해당 값으로 결측치를 채워주는 방법으로 대체)==> 결측치를 Private(특정 값이 대부분을 차지하는 경우라면 해당 값으로 결측치를 채워주는 방법으로 대체)
data['occupation'] = data['occupation'].fillna('Unknown')
# 어떤 특정값이 압도적으로 많다고 하기가 어렵다. 이런 경우에는 별도의 텍스트 'Unknown'으로 채운다.==> 어떤 특정값이 압도적으로 많다고 하기가 어렵다. 이런 경우에는 별도의 텍스트 'Unknown'으로 채운다.
data = pd.get_dummies(data , drop_first=True) #더미 변수로 변환
datadrop_first = True ==> 더미 변수의 갯수를 줄여준다.
5. 모델링 및 평가하기
from sklearn.model_selection import train_test_split
X_train , X_test , y_train , y_test = train_test_split(data.drop('class',axis =1 ) , data['class'] , test_size= 0.4 , random_state= 100)==> 독립변수('class' 열 제외한 모든 열) , 종속변수 ('class') 열
==> X_train : 학습 시킬 독립변수
==> y_train : 학습 시킬 종속변수
==> X_test : 예측 대상
==> y_test : 실제 정보
==> pred : 예측 값
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier() # 모델 객체 생성
model.fit(X_train , y_train) # 학습
pred = model.predict(X_test) # 예측
from sklearn.metrics import accuracy_score
accuracy_score(y_test , pred) # 정확도 계산
==> 0.8134309259354047
6. 분류 결정 트리
==> 분류와 회귀는 각기 다른 로직의 적용
분류 : DecisionTreeClassifier는 각 노드의 순도가 가장 높은 방향으로 분류한다.
순도 : 한 노드 안에 여러 종류가 아닌 한 종류의 목푯값만 있는 상태에 대한 지표이다.
ex) 노드 안에 사과 3개와 복숭아 3개가 있으면 두 과일이 반씩 있기 때문에 순도가 낮다. 한 노드 안에 사과 3개와 복숭아 0개가 있다면 순도가 높다고 볼 수 있다.
==> 순도를 평가하는 지표로는 지니 인덱스와 교차 엔트로피가 있다.
1> 지니 인덱스

==> 지니 인덱스는 각 노드에 대해서 계산되며, p는 노드 안에 특정 아이템의 비율이다.
EX-01 ) 사과 2, 복숭아 2 일때 계산
==> 각각 50% 이므로 , 1- (0.5**2 + 0.5**2) = 0.5
EX-02 ) 사과 1, 복숭아 3 일때 계산
==> 각각 25% , 75% 이므로 , 1- (0.25**2 + 0.75**2) = 1- 0.625 = 0.375
EX-03 ) 사과 0, 복숭아 4 일때 계산
==> 각각 0% , 100%이므로, 1 - (0**2 + 1**2) = 0
==> 순도가 높을수록 지니 인덱스는 낮은 값을 보인다.
==> 결정 트리에서는 지니 인덱스가 가장 낮은 값이 나오는 특정 변수의 특정 값을 기준으로 노드를 분류해 간다.
2> 교차 엔트로피

EX-01 ) 사과 2, 복숭아 2 일때 계산
==> 각각 50% 이므로 , - ( 0.5*Log_2(0.5) + 0.5*Log_2(0.5)) = - ( -0.5 - 0.5) = 1
EX-02 ) 사과 1, 복숭아 3 일때 계산
==> 각각 25% , 75% 이므로 , - (0.25*Log_2(0.25) + 0.75*Log_2(0.75)) = 0.81127
- (0.25*np.log2(0.25) + 0.75*np.log2(0.75))
EX-03 ) 사과 0, 복숭아 4 일때 계산
==> 각각 0% , 100%이므로, -(0*log_2(0) + 1* log_2(1) ) = 0
==> 순도가 높을수록 교차 엔트로피는 낮은 값을 보인다. ==> 최대값은 1까지 나올 수 있다.
==> 사이킷런의 결정 트리에서는 기본값으로 지니 인덱스를 사용한다.
7. 매개변수 튜닝
오버피팅 : 예측 모델이 훈련 셋을 지나치게 잘 예측한다면 새로운 데이터를 예측 할 때 큰 오차를 유발 할 수 있다.
언더피팅 : 모델이 충분히 학습되지 않아 훈련셋에 대해서도 좋은 예측력을 내지 못하는 상황이다.
==> 결정 트리에서는 트리 깊이가 깊어질 수록, 수없이 많은 노드를 분류하여 모델을 만들수록 오버피팅 발생 가능성이 높다.
==> 이 문제를 해결하기 위해 결정 트리에서는 트리의 깊이를 제한하는 매개변수를 제공한다.
model = DecisionTreeClassifier()
model.fit(X_train , y_train)
train_pred = model.predict(X_train) #훈련셋 예측
test_pred = model.predict(X_test) #시험셋 예측
print('Train score : ' , accuracy_score(y_train , train_pred) , 'Test score : ' , accuracy_score(y_test , test_pred)) # 훈련셋 , 시험셋의 정확도 평가Train score : 0.9780242279474493 Test score : 0.8147617341454676
==> 훈련셋에서는 정확도가 매우 높지만, 시험셋에서는 상대적으로 낮다. 이 정도의 격차가 발생하면 오버피팅이 발생했다고 할 수 있다.
=> 격차를 줄이기 위해 시험셋에서 정확도를 올리는 방향으로 매개변수를 설정한다.
model = DecisionTreeClassifier(max_depth= 5) #모델 객체 생성
model.fit(X_train , y_train) #학습
train_pred = model.predict(X_train) #훈련 셋 예측
test_pred = model.predict(X_test) # 시험 셋 예측
print('Train score : ' , accuracy_score(y_train , train_pred) , 'Test score : ' , accuracy_score(y_test , test_pred)) # 훈련셋 , 시험셋의 정확도 평가Train score : 0.8540180856509129 Test score : 0.8499769667809797
==> 이전보다 Train score 값이 낮 아졌다. ==> 둘 사이의 차이는 매우 낮아졌다.
model = DecisionTreeClassifier(max_depth= 7) #모델 객체 생성
model.fit(X_train , y_train) #학습
train_pred = model.predict(X_train) #훈련 셋 예측
test_pred = model.predict(X_test) # 시험 셋 예측
print('Train score : ' , accuracy_score(y_train , train_pred) , 'Test score : ' , accuracy_score(y_test , test_pred)) # 훈련셋 , 시험셋의 정확도 평가Train score : 0.8598532673605187 Test score : 0.8541741311357937
==> 이상적인 트리의 깊이를 지정하여 오버피팅을 낮추는 노력을 해야한다.
8. 트리 그래프
from sklearn.tree import plot_tree
fig = plt.figure(figsize = (15,8)) # 그래프 크기 설정
ax = plot_tree(model) # 트리 그래프 출력
plt.show()
==> 이 모델은 마지막에 훈련시킨 max_depth 7의 결과물이다.
from sklearn.tree import plot_tree
fig = plt.figure(figsize = (30,15)) # 그래프 크기 설정
ax = plot_tree(model , max_depth= 3 , fontsize = 15) # 트리 그래프 출력
plt.show()
from sklearn.tree import plot_tree
fig = plt.figure(figsize = (30,15)) # 그래프 크기 설정
ax = plot_tree(model , max_depth= 3 , fontsize = 15 , feature_names= X_train.columns) # 트리 그래프 출력
plt.show()
==> 첫 번째 노드에는 분류 기준, 지니 인덱스(gini) , 총 데이터 수(samples), value는 목표값 0과 1이 각각 몇 개씩인지를 표현
==> Married-civ-spouse <= 0.5 기준으로 나누었다. ==> 조건에 맞으면 왼쪽 , 아니면 오른쪽 분류
==> 두 번째 노드의 gini 인덱스는 0.12로 나누어졌다.(순도가 높아졌다.) ==> value값(종속변수, class)을 보면 0인 경우가 훨씬 많도록 분류 되었다.
출처 : 데싸노트의 실전에서 통하는 머신러닝
(Golden Rabbit , 저자 : 권시현)
※혼자 공부용
'머신러닝 > 머신러닝_이론' 카테고리의 다른 글
| [머신러닝 이론 01-01] 머신러닝과 통계학 (0) | 2023.03.22 |
|---|---|
| [PYTHON - 머신러닝_주성분 분석_PCA]★비지도학습★차원 축소★반영 비율 확인 (0) | 2023.01.30 |
| [PYTHON - 머신러닝_나이브베이즈]★string.punctuation 특수문자★join함수★nltk.download('stopword')★불용어★ MultinomialNB★오차행렬 (0) | 2023.01.25 |
| [PYTHON - 머신러닝_KNN알고리즘]★value_counts()★고윳값 판단★결측치★스케일링 (0) | 2023.01.24 |
| [PYTHON - 머신러닝_로지스틱선형회귀]★로지스틱 선형회귀★상관관계★원-핫 인코딩★정확도★ (1) | 2023.01.23 |
[PYTHON - 머신러닝_나이브베이즈]★string.punctuation 특수문자★join함수★nltk.download('stopword')★불용어★ MultinomialNB★오차행렬
1. 나이브 베이즈
==> 조건부 확률 기반의 분류 모델
https://knowallworld.tistory.com/232
★Multi Indexing★곱의 법칙★조건부 확률★기초통계학-[Chapter04 - 확률-04]
1. 조건부확률(Conditional Probability) ==> 0보다 큰 확률을 가지는 어떤 사건 A가 이미 발생했다는 조건 아래서, 사건 B가 일어날 확률을 의미 P(B|A) EX-01) avg_down = [24,65,14] avg = [57 , 147, 48] avg_up = [35 , 38 ,
knowallworld.tistory.com
EX) 무료라는 단어가 들어 있을 때 해당 메일이 스팸일 확률
==> 범용성이 높지는 않지만 독립변수들이 모두 독립적이라면 경쟁력있는 알고리즘
장점 :
㉠ 간단한 알고리즘에 속하며, 속도가 빠르다.
㉡ 작은 훈련셋으로도 잘 예측한다.
단점 :
㉠ 모든 독립변수가 각각 독립적임을 전제로 한다. ==> 실제 데이터가 독립적이지 않으면 문제 발생
2. 데이터 확인
data['target'].value_counts()
==> 고윳값 2개 (ham , spam)
3. 전처리
import string
string.punctuation #특수 기호 목록 출력sample_string = data['text'].loc[0]
for i in sample_string:
if i not in string.punctuation:
print(i)==> 특수문자 제외하고 출력
new_string = ''.join(new_string)
new_string==> join함수 활용하여 문자열 붙이기
data['text'].apply(remove_punc)==> apply 함수를 활용하여 데이터프레임의 한 줄 한 줄을 따로 함수에 적용시킨다.
4. 전처리 : 불용어 제거
==>불용어(stopword) ==> 자연어 분석에 큰 도움이 안되는 단어
import nltk
nltk.download('stopwords') # 불용어 목록 갖고 오기from nltk.corpus import stopwords #불용어 목록 임포트
stopwords.words('english') #영어 불용어 선택['i',
'me',
'my',
'myself',
'we',
'our',
'ours',
'ourselves', ......]
==> 한국어 불용어의 경우 되지 않는다. ==> www.ranks.nl 등에서 받는다.
sample_string = data['text'].loc[0]
sample_string.split() #단어 단위로 문장 분할
for i in sample_string.split() :
if i.lower() not in stopwords.words('english'): #불용어가 아니라면 소문자로 변환
print(i.lower())== stopwords.words('english') ==> 불용어 목록
go
jurong
point
crazy
available
bugis
def stop_words(x):
new_string = []
for i in x.split() : #순회
if i.lower() not in stopwords.words('english'):
new_string.append(i.lower()) #문자 단위로 추가
new_string = ' '.join(new_string)
return new_string
data['text'] = data['text'].apply(stop_words) #텍스트에 stop_words 함수 적용
data['text']==> 불용어 제거한 문장 출력
5. 전처리 : 목표 컬럼 형태 변경하기
map()함수 : 딕셔너리 타입의 데이터를 사용하여 매칭되는 값을 불러오도록 사용할 수 있다.
data['target'] = data['target'].map({'spam' : 1 , 'ham' : 2}) #텍스트를 숫자로 변환
data['target']
6. 전처리 : 카운트 기반으로 벡터화 하기
==> 문자를 개수 기반으로 벡터화 하기
==> 데이터 전체에 존재하는 모든 단어들을 사전처럼 모은 뒤에 인덱스를 부여하고, 문장마다 속한 단어가 있는 인덱스를 카운트하는 것이다.
x = data['text'] #독립변수
y = data['target'] #종속변수
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer() # 객체 생성
cv.fit(x) #학습하기
cv.vocabulary_ #단어와 인덱스 출력==> sklearn.feature_extraction.text 라이브러리의 CountVectorizer 모듈 임포트한다.
{'go': 3791,
'jurong': 4687,
'point': 6433,
'crazy': 2497,
'available': 1414,
'bugis': 1881,
'great': 3888,
'world': 9184,
'la': 4847, ... } ==> 단어와 인덱스 출력
x = cv.transform(x) #transform
print(x) # (데이터의 행 번호(데이터 프레임의 행 번호) , 단어의 인덱스 값) 행에서 출현 횟수(0, 1181) 1
(0, 1414) 1
(0, 1879) 1
(0, 1881) 1
(0, 2214) 1
(0, 2497) 1
(0, 3791) 1
(0, 3848) 1
(0, 3888) 1
(0, 4687) 1
==> (데이터의 행 번호(데이터 프레임의 행 번호) , 단어의 인덱스 값) 행에서 출현 횟수
print(cv.vocabulary_['go'])
print(cv.vocabulary_['jurong'])
print(cv.vocabulary_['point'])3791
4687
6433
==> 인덱스값 출력
7. 모델링 및 예측/평가하기
from sklearn.model_selection import train_test_split
X_train , X_test , y_train , y_test = train_test_split(x,y , test_size= 0.2 , random_state= 100) #학습셋 시험셋 분활
from sklearn.naive_bayes import MultinomialNB # 나이브 베이즈 알고리즘으로 MultinomialNB 모듈 사용한다.
#==> 다항분포(Multinormial)외에 정규분포 베르누이분포에 따른 NB 모듈이 있다.
model = MultinomialNB() #모델 객체 생성
model.fit(X_train , y_train) #학습
pred = model.predict(X_test) #예측
from sklearn.metrics import accuracy_score , confusion_matrix
print(f'정확도 계산 : {accuracy_score(y_test, pred)}') # 정확도 계산
print(confusion_matrix(y_test , pred)) # 혼동(오차) 행렬 출력==> MultinomialNB ==> 나이브 베이즈 알고리즘
==> confusion_matrix() ==> 오차 행렬 출력
정확도 계산 : 0.9856502242152466
[[134 4]
[ 12 965]]
| 0 | 1 | |
| 0 | 134 | 4 |
| 1 | 12 | 965 |
==> 실제값이 0 이고, 예측값이 0인 경우는 134건
==> 실제값이 1이고, 예측값이 1인 경우는 965건이다.
sns.heatmap(confusion_matrix(y_test , pred) , annot= True , fmt= '.0f')
제 1 종 오류 : 실제 음성인 것을 양성으로 예측하는 오류
제 2 종 오류 : 실제 양성인 것을 음성으로 예측하는 오류
EX) 건강한 사람(음성) ==> 당신은 코로나19에 걸렸다.(양성) ==> 음성인데 양성으로 판단( 제 1종오류 , 거짓 양성)
코로나에 걸린 사람(양성) ==> 당신은 건강하다.(음성) ==> 양성인데 음성으로 판단(제 2종오류 , 거짓 음성)
8. 나이브 베이즈 모델
https://knowallworld.tistory.com/233
★독립사건 종속사건★조건부 확률★기초통계학-[Chapter04 - 확률-05]
1. 독립사건 ==> 사건 A의 발생 여부가 다른 사건 B가 나타날 확률에 아무런 영향을 미치지 않을 때 https://knowallworld.tistory.com/189 ==> 참고 EX ) 사건 A와 사건 B가 독립이다 2. 종속사건 ==> 사건 A의 발
knowallworld.tistory.com
어떤 사건 A가 이미 발생했다는 조건 아래서, 사건 B가 일어날 확률을 의미 ==> P(B|A)
P(A | B) : 사후확률 ==> B가 발생했을 때, A가 발생할 확률 ==> 스팸문자의 B라는 특정 단어가 등장했을 때, A가 스팸일 확률
P(A) : 사전확률 ==> B의 발생유무와 관련없이 기본적으로 A가 발생할 확률로서 , 전체 문자 중 스팸문자의 비율
P(B|A) : 우도(Likelihood) 혹은 가능도, A가 발생했을 때 , B가 발생할 확률, 스팸 메일인 경우 B라는 특정 단어가 들어 있을 확률
P(B) : 전체에서 B가 발생할 확률, 전체 문자에서 B라는 특정 단어가 들어 있을 확률

# 1. 청소년중 1명 선택 ==> 염색을 원할 확률 ==> P(청소년 | 하고 싶다.) =
p_handa = round(A.loc['합계' , '하고 싶다.'] , 4)
print(p_handa)
# 2. 남자가 선정 ==> 이 사람이 염색을 원할 확률 ==> P(남자 | 하고 싶다.) =
P_nam_handa = round(A.loc['남자' , '하고 싶다.'] / A.loc['남자' , '합계'] , 4)
print(P_nam_handa)
# 3. 여자가 선정 ==> 이 사람이 염색을 원할 확률 ==> P(여자 | 하고 싶다.) =
P_woman_handa = round(A.loc['여자' , '하고 싶다.'] / A.loc['여자' , '합계'] , 4)
print(P_woman_handa)==> '합계' 행의 '하고싶다.' 열
출처 : 데싸노트의 실전에서 통하는 머신러닝
(Golden Rabbit , 저자 : 권시현)
※혼자 공부용
'머신러닝 > 머신러닝_이론' 카테고리의 다른 글
[PYTHON - 머신러닝_KNN알고리즘]★value_counts()★고윳값 판단★결측치★스케일링
1. 고윳값 판단
data['class'].unique() # 목표 변수의 고윳값 출력 ==> 0과 1로 이루어진 이진변수가 아닌 3개이상으로 이루어진 범주형 변수==> array([0,1,2])
data['class'].nunique() # 고윳값의 갯수 ==> 와인을 3개의 등급으로 나눈다.==> 3
data['class'].value_counts() # 각 고윳값에 해당하는 개수 출력
fig = plt.figure(figsize = (15,8))
ax = sns.countplot(data['class'])ax = sns.barplot(x = data['class'].value_counts().index , y=data['class'].value_counts())==> barplot, countplot 둘다 동일한 결과값 얻을 수 있다.

2. 결측치 제거
data.dropna(subset = ['alcohol'])==> 지정된 변수의 결측치 행만 제거하기 ==> alcohol의 열의 결측치 존재하는 행 제거
data.drop(['alcohol' , 'nonflavanoid_phenols'] , axis = 1) #변수를 제거하기==> 아예 열 제거
data.fillna(data.mean()) #평균적으로 결측치 채우기==> 결측치에 대해 해당 열의 평균으로 대체
1. 일반적으로 dropna()를 사용하여 결측치 행 채우기
2. 통상적으로 결측치가 데이터의 50%이상이면 drop()을 고려해볼 만하고, 70~80%이 상이면 drop()을 적용하는 것이 좋다. ==> 결측치가 너무 많으면 삭제하는 것이 좋다.
3. 결측치의 경우 평균을 채워넣는다 하더라도 노이즈 발생 가능성 ==> 중위값 사용도 가능
data.fillna(data.median() , inplace=True) #평균적으로 결측치 채우기3. 스케일링
==> 스케일링은 데이터의 스케일(scale)을 맞추는 작업
KNN 알고리즘의 경우 거리기반 알고리즘
==> alcohol 열의 최솟값 : 11.03, 최대값 : 14.75
==> magnesium(최솟값 : 70 , 최대값 : 162)에서의 1은 완전 다른 영향을 미친다.
==> 왜곡된 예측 가능
from sklearn.preprocessing import StandardScaler, MinMaxScaler , RobustScaler
#한 라이브러리에서 여러 모듈 임포트==> 사이킷런 라이브러리의 preprocessing 모듈 사용
4. 표준화 스케일링
==> 평균이 0이 되고, 표준편차가 1이 되도록 데이터를 고르게 분포시키는데 사용
==> 데이터에 아웃라이어가 존재할 때 아웃라이어의 영향을 받는다. 평균 0, 분산 1이 되게끔 분포시키기 때문에, 데이터의 기존 분포 형태가 사라지고 정규분포를 따르는 결과물을 가져온다.
st_scaler = StandardScaler() #스케일러 지정st_scaler.fit(data) # 학습, 스케일링에 필요한 정보(평균 , 표준편차)가 학습된다.st_scaled = st_scaler.transform(data) #학습에서 얻은 정보 계산st_scaled
pd.DataFrame(st_scaled , columns = data.columns)
https://knowallworld.tistory.com/254
정규분포의 표준정규분포로의 변환★기초통계학-[Chapter06 - 연속확률분포-03]
1. 정규분포와 표준정규분포의 관계 =========================== ==> P(z_a =2.5 , facecolor = 'skyblue') # x값 , y값 , 0 , x= 2.5) = P(Z 박테리아의 수가 75마리 이상 103마리 이하일 확률 P(75
knowallworld.tistory.com

==> fit() 함수로 학습을 시켜주는 과정에서 각 컬럼의 평균과 표준편차가 st_scaler에 기억되고, transform()을 적용하면 그 값들을 이용하여 위의 수식으로 연산
round(st_scaled.describe(), 2)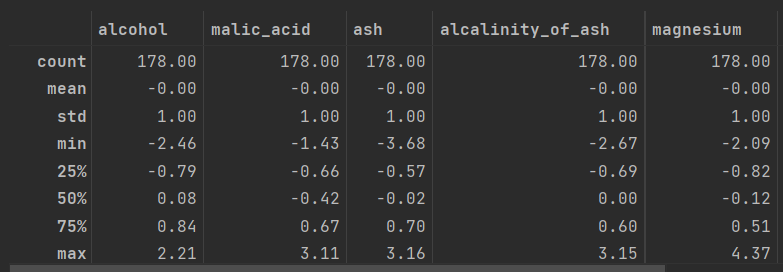
5. 로버스트 스케일링
==> 데이터에 아웃라이어가 존재하고, 그 영향력을 그대로 유지하고 싶을 때 사용
rb_scaler = RobustScaler() #로버스트 스케일링에 사용할 객체를 생성rb_scaled = rb_scaler.fit_transform(data) #로버스트 스케일링 ==> fit과 transform이 합쳐졌다.
rb_scaled = pd.DataFrame(rb_scaled , columns = data.columns)round(rb_scaled.describe(), 2)==> 평균과 표준편차 대신 사분위값을 이용하여 계산한다.
==> 데이터에 아웃라이어가 존재할 때, 아웃라이어의 영향을 받지 않는다. 변환된 데이터의 범위는 표준화 스케일링이나 최소-최대 스케일링보다 넓게 나타난다.
6. Min-Max 스케일링
==> 데이터 분포의 특성을 최대한 그대로 유지하고 싶을 때 사용
mm_scaler = MinMaxScaler() #최소-최대 스케일링 객체 생성
mm_scaled = mm_scaler.fit_transform(data) # 최소-최대 스케일링
mm_scaled = pd.DataFrame(mm_scaled , columns= data.columns)
round(mm_scaled.describe() , 2)==> 최소-최대 스케일링의 특징은 모든 컬럼에서 최댓값이 1 , 최솟값이 0인 형태로 변환된다는 것이다.
==> 각 값에서 최솟값을 빼주고, 최대값의 차이만큼 나눠준다.

==> 표준화 스케일링과 마찬가지로 아웃라이어의 영향을 받게 된다. 위의 두 스케일러와 비교했을 때 데이터의 기존 분포를 가장 있는 그대로 담아내며, 스케일만 변화시킨다. 데이터의 범위는 0~ 1이다.
7. 정규화 스케일링
==> 행 기준의 스케일링이 필요할 때 사용, 거의 사용X
8. 스케일링 적용
round(mm_scaled.describe() , 2)
#%%
from sklearn.model_selection import train_test_split
X_train , X_test, y_train , y_test = train_test_split(data.drop('class' , axis= 1) , data['class'] , test_size=0.2, random_state=100) #학습셋과 시험셋 분리==> 데이터 셋 분할
==> test_size (시험 셋) ==> 20% , random_state = 100 ==> 랜덤 샘플링
==> 랜덤 샘플링이란 데이터를 특정 비율로 나눌 때 마구잡이로 뒤섞어서 나누는 것
https://knowallworld.tistory.com/371
[PYTHON - 머신러닝_선형회귀]★선형회귀★seaborn 타원만들기★모델 평가방법 RMSE , R**2★model.coef_(
1. 선형회귀 ==> 가장 기초적인 머신러닝 모델 ==> 여러가지 데이터를 연속형 변수인 목표 변수를 예측해 내는 것이 목적이다. ==> 몸무게, 나이 , BMI, 성별 등의 데이터를 활용하여 연속형 변수를
knowallworld.tistory.com
1> 하이퍼 파라미터 튜닝하기
knn = KNeighborsClassifier() #KNN 모델 생성
knn.fit(X_train_scaled , y_train) #학습
pred = knn.predict(X_test_scaled) #예측
predfrom sklearn.metrics import accuracy_score
accuracy_score(y_test , pred)==> y_test와 예측값인 pred가 얼마나 일치하는지 알아보기 위하여 accuracy_score 사용
score = []
for i in range(1, 21):
knn = KNeighborsClassifier(n_neighbors= i) # knn 모델 생성
knn.fit(X_train_scaled , y_train)
pred = knn.predict(X_test_scaled)
score.append(accuracy_score(y_test, pred))
score==> 최적의 가중 매개변수 선택하기
9. K-최근접 이웃
==> KNN 알고리즘은 새로운 데이터를 예측할 때 , 거리를 기반으로 하여 인접한 데이터와 같은 종류로 분류
출처 : 데싸노트의 실전에서 통하는 머신러닝
(Golden Rabbit , 저자 : 권시현)
※혼자 공부용
'머신러닝 > 머신러닝_이론' 카테고리의 다른 글
[PYTHON - 머신러닝_로지스틱선형회귀]★로지스틱 선형회귀★상관관계★원-핫 인코딩★정확도★
1. 로지스틱 회귀
==> 로지스틱 회귀 또한 선형 회귀처럼 기본 분석 모델이다.
==>선형 회귀 분석은 연속된 변수를 예측하는 반면 , 로지스틱 회귀 분석은 Yes/No처럼 2가지로 나뉘는 분류 문제를 다룬다.
==> 실제 이진분류가 필요한 상황이 많기 때문에 2가지 범주를 구분하는 간단한 예측에 유용하며 딥러닝의 기본지식이다.
장점 : 선형 회귀분석만큼 구현에 용이 , 계수(기울기)를 사용해 각 변수의 중요성을 쉽게 파악가능
단점 : 선형 회귀분석을 근간으로 하고 있기 때문에, 선형 관계가 아닌 데이터에 대한 예측력이 떨어진다.
Yes/No, True/False와 같은 2가지 범주로 나뉜 값을 예측하는데 사용
분류 문제에 있어서 기준선으로 자주 활용
3. 상관관계
data.corr() # 상관관계 출력
==> 상관관계는 숫자가 아니라면 계산이 안된다
==> 문자형 변수들을 제거하고 상관관계를 보여준다.
==>0에 가까울수록 상관관계가 없는 것이고, 1 혹은 -1에 가까울수록 상관관계가 크다.
==>양수는 정수적 상관, A가 증가하면 B도 함께 증가
==>음수는 부적 상관으로 A가 증가할수록 B가 감소하는 경우이다.
==>가장 큰 상관관계를 보이는 부분은 Parch(함께 탑승한 부모 및 자녀의 수)와 SibSp(함께 탑승한 형제 및 배우자 수)이다. ==> 0.414542
#0.2 이하 : 상관관계가 거의 없음
#0.2 ~ 0.4 : 낮은 상관관계
#0.4 ~ 0.6 : 중간 수준의 상관관계
#0.6 ~ 0.8 : 높은 상관관계
#0.8 이상 : 매우 높은 상관관계
sns.heatmap(data.corr())
plt.show()
sns.heatmap(data.corr() , cmap = 'coolwarm')
plt.show()
#히트맵에 대한 0을 기준으로 대칭이 되는 색상 배열 사용
3. 전처리: 범주형 변수 변환하기(더미 변수와 원-핫 인코딩)
==>파이썬은 자료형이 object인 변수들 , 데이터가 숫자가 아닌 문자인 변수를 이해 못한다.
EX) object형을 숫자로 대체하는 방법, 계절의 경우 봄,여름,가을,겨울을 각각 1,2,3,4로 변환
==> BUT. 상대적인 서열로 인식의 단점 존재
EX-02) 기존의 하나던 컬럼을 MALE과 FEMALE 컬럼으로 분리

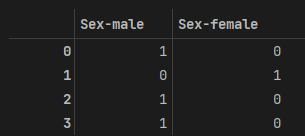
==> 문자로 된 값을 숫자화하여 이해할 수 있게 한다. ==> 더미 변수를 만든다 or 원-핫 인코딩이라 한다.
==> 고유값
data['Name'].nunique()==> 889 ==> 고윳값이 수백 가지이므로 더미 변수로 변환시키기엔 컬럼이 너무 많다. ==> 이름에 따라 사망 여부가 갈린다고 추론하기엔 어렵다. ==> 삭제
data['Sex'].nunique()==> 2
data['Ticket'].nunique()==> 680 ==> 고윳값 수백가지 ==> 티켓에 따른 사망률 추론 어려우므로 삭제
data['Embarked'].nunique()==> 3
pd.get_dummies(data, columns = ['Sex' , 'Embarked'])==> 더미변수 화

==> 남자/여자 (0,1)로 구분
==> Embarked ==> 고윳값 3개
pd.get_dummies(data, columns = ['Sex' , 'Embarked'] , drop_first=True)
==> drop_first = True로 더미변수의 data를 줄인다.
4. 모델링 및 예측하기
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
X = data.drop('Survived' , axis = 1) #데이터셋에서 종속변수 제거
y = data['Survived'] #종속변수 저장
X_train ,X_test , y_train , y_test = train_test_split(X , y, test_size= 0.2 , random_state= 100)model = LogisticRegression() #로지스틱 회귀 모델 생성
model.fit(X_train , y_train) #모델 학습
pred = model.predict(X_test) #예측5. 예측 모델 평가하기
==> 이진 분류의 경우 RMSE는 적합하지 않다.
https://knowallworld.tistory.com/371
[PYTHON - 머신러닝_선형회귀]★선형회귀★seaborn 타원만들기★모델 평가방법 RMSE , R**2★model.coef_(
1. 선형회귀 ==> 가장 기초적인 머신러닝 모델 ==> 여러가지 데이터를 연속형 변수인 목표 변수를 예측해 내는 것이 목적이다. ==> 몸무게, 나이 , BMI, 성별 등의 데이터를 활용하여 연속형 변수를
knowallworld.tistory.com
==> 평균 제곱 오차 ==> 실제값과 예측값 사이의 오차를 제곱한 뒤 이에 대한 평균 계산
==> 이진분류 평가 지표로는 정확도, 오차행렬 ,정밀도 , 재현율 , F1-Score , 민감도 , 특이도, AUC 등이 있다.
6. 예측 모델 평가하기_ 정확도
from sklearn.metrics import accuracy_score #정확도 라이브러리 임포트
accuracy_score(y_test , pred) # 실제값과 예측값으로 정확도 계산0.7808988764044944
==> 78%의 정확도 ==> 정확도의 좋고 나쁨을 결정하는 절대적인 지표는 없다.
==> 고윳값이 10개라면 상대적으로 낮은 정확도도 용인 될 수 있다.
==> 고윳값이 2개인 이진분류에서도 각각의 비율이 어떠한가에 따라 평가 기준이 달라진다.
==> ex) 0이 95%이고, 1이 5%로 구성된 이진분류라면, 정확도가 90%라고 해도 좋은 값으로 볼 수 없다.
==> 왜냐하면 머신러닝 모델 없이 모든 값을 0으로 예측한다면 정확도는 95%라고 할 수 도 있다.
==> 고윳값의 비율이 50:50 이라면 80% 이상의 정확도 정도면 나쁘지 않고, 90% 이상의 정확도를 얻어야 괜찮은 결과로 보는 편이다.
==> XGBoost 나 LightGBM을 사용하면 더 좋은 정확도를 얻을 수 있다.
pd.Series(model.coef_[0] , index = X.columns)
==> 로지스틱 회귀 분석 결과 Pclass의 값이 커질수록 생존률이 낮아진다.
7. 피처 엔지니어링
==> 기존 데이터를 손보아 더 나은 변수를 만드는 기법
==> 더미변수를 만드는 일도 일종의 피처 엔지니어링이다.
==> 피처란? 독립변수의 다른 표현
==> 선형 회귀 분석과 로지스틱 회귀 분석을 선형 모델이라고 하는데, 선형 모델에서는 다중공선성 문제를 주의해야한다.
==> 다중공선성은 독립변수 사이에 상관관계가 높은 때에 발생하는 문제
==> ex) A와 B의 상관관계가 매우 높다면, y가 증가한 이유가 A때문인지 B때문인지 명확하지 않다.
==> 다중공선성 문제는 상관관계가 높은 변수 중 하나를 제거하거나, 둘을 포괄하는 새로운 변수를 만들거나 , PCA와 같은 방법으로 차원 축소를 수행해야한다.

==> Parch와 SibSp 간의 상관관계가 높다. ==> 이를 새로운 변수로 생성
data['family'] = data['SibSp'] + data['Parch'] #SibSp와 Parch 변수 합치기
data.drop(['SibSp' , 'Parch'] , axis = 1 , inplace =True) #Sibsp , Parch 변수 삭제
data.head()
X = data.drop('Survived' , axis = 1) #데이터셋에서 종속변수 제거
y = data['Survived'] #종속변수 저장
X_train ,X_test , y_train , y_test = train_test_split(X , y, test_size= 0.2 , random_state= 100)
model = LogisticRegression() #로지스틱 회귀 모델 생성
model.fit(X_train , y_train) #모델 학습
pred = model.predict(X_test) #예측
accuracy_score(y_test , pred) # 실제값과 예측값으로 정확도 계산0.7921348314606742
==> 독립변수의 수가 하나 줄었지만 기존보다 정확도가 0.012정도 높아졌다.
==> 모델링은 한 번만에 끝내는 것이 아닌 다양한 시도를 해가며 재반복해 더 나은 결과물을 얻어내가는 과정
8. 로지스틱 회귀 분석 공식

출처 : 데싸노트의 실전에서 통하는 머신러닝
(Golden Rabbit , 저자 : 권시현)
※혼자 공부용
'머신러닝 > 머신러닝_이론' 카테고리의 다른 글
[PYTHON - 머신러닝_선형회귀]★선형회귀★seaborn 타원만들기★모델 평가방법 RMSE , R**2★model.coef_(기울기)★model.intercept_(y절편)
1. 선형회귀
==> 가장 기초적인 머신러닝 모델
==> 여러가지 데이터를 연속형 변수인 목표 변수를 예측해 내는 것이 목적이다.
==> 몸무게, 나이 , BMI, 성별 등의 데이터를 활용하여 연속형 변수를 예측
==> 복잡한 알고리즘에 비해서는 예측력이 떨어지지만 데이터의 특성이 복잡하지 않을 때는 쉽고 빠른 예측이 가능하다.
2. 전처리 : 학습 set , Train set 나누기
| 독립변수 | 종속변수 | |
| 학습셋 | X_train | Y_train |
| 시험셋 | X_test | Y_test |
==> 데이터를 나누는 작업은 크게 2가지 차원으로 진행되어 총 4개 데이터셋으로 나눈다.
학습셋 과 시험셋 나누는 이유 :
==> 학습셋과 시험셋을 구분하지 않고 예측 모델을 만든다면, 학습에 사용한 데이터와 평가용으로 데이터가 동일하다는 것으로 모델을 만들고 나서 새로운 데이터에도 맞는지 검증이 안되기 때문이다.
==> 검증하지 않은 상태라는 불확실성을 줄일 목적으로 준비하는 것이 시험셋이다.
==> 학습셋 데이터는 모델을 학습시키는 데 사용하고, 나머지 데이터는 모델 학습이 완료된 이후에 평가용으로 사용할 수 있다.
==> 시험셋의 데이터는 처음 만나게 되는 데이터로 예측/평가를 했을 때도 예측력이 좋게 나타나면, 향후 예측하게 될 새로운 데이터에 대해서도 잘 작동할 수 있다.
==> 일반적으로 학습 셋 : 시험 셋을 각각 7:3 혹은 8:2 정도 비율로 나눈다.
==> 전체 데이터 크기가 작다면 학습셋 비율을 높여서 최대한 학습셋을 많이 확보해야한다.
file_url = 'https://media.githubusercontent.com/media/musthave-ML10/data_source/main/insurance.csv'
data = pd.read_csv(file_url)
data
data.info() # column(열) 정보 , 결측치 아닌것들 COUNT , 자료형
round(data.describe(), 2) #소수점 2자리까지만 통계정보량 출력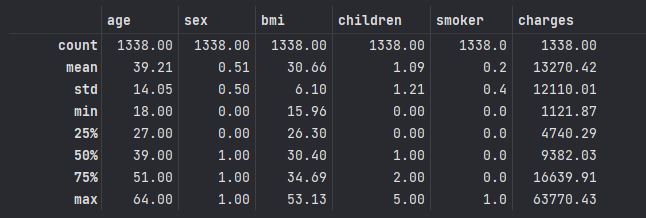
from sklearn.model_selection import train_test_split #사이킷런 importX = data[['age' , 'sex' , 'bmi' , 'children' , 'smoker']] #독립변수
y = data['charges'] #종속변수
X_train , X_test , y_train , y_test = train_test_split(X , y , test_size=0.2 , random_state= 100) #데이터 셋 분할
# test_size (시험 셋) ==> 20% , random_state = 100 ==> 랜덤 샘플링
#랜덤 샘플링이란 데이터를 특정 비율로 나눌 때 마구잡이로 뒤섞어서 나누는 것
#랜덤 샘플링을 진행하지 않는다면 데이터가 특정 순서로 정렬될 수 도 있다.
==> Random Sampling ==> 랜덤 샘플링이란 데이터를 특정 비율로 나눌 때 마구잡이로 뒤섞어서 나누는 것 ==> 랜덤 샘플링을 진행하지 않는다면 데이터가 특정 순서로 정렬될 수 도 있다.
==> train_test_split() 함수는 기존 데이터의 순서와 상관없이 마구잡이로 섞어서 데이터를 분류시킨다.
==> random_state 옵션은 랜덤하게 샘플링하면서도 지속적으로 같은 데이터 분류가 가능하도록 한다.
3. 모델링
==> 모델링은 머신러닝 알고리즘으로 모델을 학습시키는 과정이며, 그 결과물이 머신러닝 모델이 된다. 모델링에 사용할 머신러닝 알고리즘을 선택하고, 독립녀수와 종속변수를 fit() 함수에 인수로 주어 학습한다.
from sklearn.linear_model import LinearRegression==> sklearn.linear_model 모듈에서 LinearRegression 라이브러리를 불러온다.
model = LinearRegression() #선형회귀에 사용할 model 객체를 생성했으니 model 객체를 사용해서 선형 회귀로 학습하고 예측할 수 있게 된다.and
model.fit(X_train , y_train)
#객체.fit(독립변수, 종속변수)학습시킨다 의 의미 : 데이터를 모델 안에 넣어서 독립변수와 종속변수 간의 관계들을 분석해 새로운 데이터를 예측할 수 있는 상태로 만드는 것이다.
4. 모델을 활용해 예측하기
pred = model.predict(X_test)==> predict()함수로 예측을 할 수 있으며, 괄호 안에는 예측 대상을 넣어주면 된다.
5. 예측 모델 평가하기
==> 모델을 평가하는 방법으로 '테이블로 평가하기' , '그래프로 평가하기' , '통계(RMSE)적인 방법으로 평가하기'가 있다.
1> 테이블로 평가하기
comparison = pd.DataFrame({'actual' : y_test, 'pred' : pred})
comparison예측한 값은 pred에 , 실제 정보는 y_test에 저장되어 있다.
예측값이 얼마나 정확한지는 pred와 y_test를 비교하는 것으로 단순하게 확인할 수 있다.

2> 그래프로 평가하기
fig = plt.figure(figsize=(15,8))
x = comparison.iloc[:, 0].tolist()
y = comparison.iloc[: ,1].tolist()
# ax = sns.set_style('whitegrid')
ax = sns.scatterplot(x= x , y = y)
# ax = sns.lineplot(x= 'actual' , y = 'pred' , data = comparison)
ax.set_title('예측값 , 관찰값 산정' , fontsize=15)
ax.set_xlabel('실제값', fontsize = 15 , fontweight = 'bold')
ax.set_ylabel('예측값' , fontsize = 15 , fontweight = 'bold' , rotation = 0 , labelpad=25)
#####1번째
g_ell_center = (10000, 11000)
g_ell_width = 30000
g_ell_height = 8000
angle = 45.
g_ellipse = patches.Ellipse(g_ell_center, g_ell_width, g_ell_height, angle=angle, fill=False, edgecolor='red', linewidth=2)
ax.add_patch(g_ellipse)
plt.annotate('' , xy=(25000, 3000), xytext=(18000 , 8000) , arrowprops = dict(facecolor = 'black'))
ax.text(25000 ,3000 , '실제값과 예측값이 비슷하다.' , fontsize = 13)
#####2번째
g_ell_center = (22000, 32000)
g_ell_width = 30000
g_ell_height = 8000
angle = 40.
g_ellipse = patches.Ellipse(g_ell_center, g_ell_width, g_ell_height, angle=angle, fill=False, edgecolor='green', linewidth=2)
ax.add_patch(g_ellipse)
plt.annotate('' , xy=(10000, 35000), xytext=(13000 , 30000) , arrowprops = dict(facecolor = 'black'))
ax.text(5000 ,37000 , '실제값보다 예측값이 더 높게 나타났다.' , fontsize = 13)
#####3번째
g_ell_center = (42000, 32000)
g_ell_width = 30000
g_ell_height = 8000
angle = 40.
g_ellipse = patches.Ellipse(g_ell_center, g_ell_width, g_ell_height, angle=angle, fill=False, edgecolor='blue', linewidth=2)
ax.add_patch(g_ellipse)
plt.annotate('' , xy=(50000, 25000), xytext=(48000 , 30000) , arrowprops = dict(facecolor = 'black'))
ax.text(45000 ,22000 , '실제값보다 예측값이 더 높게 나타났다.' , fontsize = 13)==> patches 모듈로 다각형 그릴 수 있다.

3> 통계적인 방법으로 평가하기 : RMSE
==>연속형 변수를 예측하고 평가할 때 가장 흔하게 쓰이는 RMSE(Root Mean Squared Error) 루트 평균 제곱근 오차, 평균 제곱근 편차를 사용
https://knowallworld.tistory.com/224
★vlines()★선형회귀★평균제곱 오차(MSE)★Tensorflow이용 머신러닝-[Chapter 03-01]딥러닝★
1. 가장 훌륭한 예측선 긋기 : 선형 회귀 ==> 딥러닝은 자그마한 통계의 결과들이 무수히 얽히고 설켜 이루어지는 복잡한 연산 ==> 가장 말단에서 일어나는 2가지 계산원리 ==> '선형회귀' , '로지스
knowallworld.tistory.com

==> 평균 제곱 오차 ==> 실제값과 예측값 사이의 오차를 제곱한 뒤 이에 대한 평균 계산

==> 루트 평균 제곱 오차 ==> MSE에 루트를 씌운 값으로 가장 릴반적으로 사용
from sklearn.metrics import mean_squared_error # MSE 라이브러리
mean_squared_error(y_test,pred)**0.5 # RMSE를 위한 루트 씌우기mean_squared_error(y_test,pred, squared= False)
4> 통계적인 방법으로 평가하기 : R**2(결정계수)
==> 독립변수로 설명되는 종속변수의 분산비율 나타낸다.
SST(Sum of Squares Total) ==> 종속변수 y의 평균값과 관측치의 거리
SSR(Sum of Squares Regression) ==> 평균으로 대충 맞추었을 때와 우리가 만든 모델을 이용했을 때의 차이
SSE(Sum of Squares Error) ==> 선형 회귀 모델과 관측치와의 거리
R**2 = SSR/ SST
==> 대충 평균값으로 넣었을 때 , 예측값(평균 값) 과 실젯값의 차이 중 우리 모델이 얼마만큼의 비율로 실젯값에 가깝게 예측하는지를 의미.
model.score(X_train , y_train)0.736822
==> R**2은 비율이므로 최대 1까지 나올 수 있으며, 좋은 모델일수록 1에 가깝다.
==> 0.7~0.8 이상이면 일반적으로 괜찮은 수치라고 할 수 있다.
6. 선형 회귀
==> 선형회귀(Linear Regression)은 독립변수와 종속변수 간에 선형 관계가 있음을 가정하여 최적의 선을 그려서 예측하는 방법.
==> 머신러닝에서는 손실 함수(Loss Function)을 최소화하는 선을 찾아서 모델을 만들어낸다.
==> 손실 함수란? : 예측값과 실제값의 차이, 즉 오차를 평가하는 방법
(ex.MSE 나 RMSE)
수식 표현 :
==> 독립변수가 'age' , 'sex' , 'bmi' , 'children' , 'smoker'로 5개의 모델을 생성.
==> 청구비용 = A * age + B * sex + C * bmi + D *children + E * smoker + i
pd.Series(model.coef_ , index = X.columns)
==> A,B,C,D,E는 각 독립변수에 대한 기울기이다.
==> 이 기울기 값을 계수라고도한다.
==> 종속변수(charges)는 age가 1만큼 증가하면 약 265만큼 증가한다.
==> 성별(sex)의 경우에는 0과 1로 구성된 명목데이터 이기 때문에 , 남자(1)의 경우 여자(0)보다 charges가 보통 17높다.
model.intercept_-11576.99997611236
==> 모델의 y절편
charges = 264.799803 * age + 17.344661*sex + 297.514806*bmi + 469.339602*children + 23469.280173*smoker - 11576.99997611236
==> 데이터의 특정 행을 정해서 각 변수의 값을 위 수식에 넣으면 모델이 보여주는 예측값과 같은 결과를 얻을 수 있다!
==> 선형 회귀는 수식을 도출하기 매우 쉬워 그 해석도 직관적이다.
출처 : 데싸노트의 실전에서 통하는 머신러닝
(Golden Rabbit , 저자 : 권시현)
※혼자 공부용
'머신러닝 > 머신러닝_이론' 카테고리의 다른 글
[PYTHON- 기초통계 -02]★데이터프레임 추출★
1. 데이터프레임
x = np.array([1,2,3,4,5])
sample_df = pd.DataFrame({
'col1' : x,
'col2' : x+2,
'col3' : ["a" , "b" , "c" , "d" , "e"]
})
sample_df
1> 데이터프레임 sample_df에서 지정한 열만 빼고 추출
sample_df.drop('col3' , axis = 1)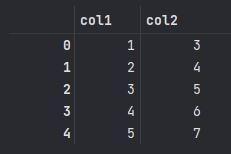
2> index 사용하여 추출
sample_df.query('index == 0')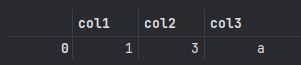
3> 해당 열변수의 값이 특정한 경우
sample_df.query('col3 == "b"')
'PYTHON-기초통계 > PYTHON 라이브러리' 카테고리의 다른 글
| [PYTHON- 라이브러리]★PDF to DataFrame★ (0) | 2024.04.11 |
|---|---|
| [PYTHON- 기초통계 -01]★클래스와 인스턴스★유용한 라이브러리★numpy활용★벡터 기본연산★결측값 (1) | 2023.01.19 |