[PYTHON - 머신러닝_K-MEAN 군집화]★엘보우 기법
1.K-MEAN 군집화
==> 비지도 학습의 대표적인 알고리즘 중 하나로 목표 변수가 없는 상태에서 데이터를 비슷한 유형끼리 묶어내는 머신러닝 기법이다.
==> K-최근접 이웃 알고리즘과 비슷하게 거리기반으로 작동하며 적절한 K값을 사용자가 지정해야한다.
==> 거리 기반으로 작동하기 때문에 데이터 위치가 가까운 데이터끼리 한 그룹으로 묶는다.(K 값은 전체 그룹의 수)
클러스터링 : 수많은 데이터를 하나하나 직접 살펴보기보단 적절한 그룹으로 나누고 특징을 살펴볼 수 있다.
장점 :
㉠ 구현이 비교적 간단하다.
㉡ 클러스터링 결과를 쉽게 해석할 수 있다.
단점 :
㉠ 최적의 K값을 자동으로 찾지 못하고, 사용자가 직접 선택해야 한다.
㉡ 거리기반 알고리즘이기 때문에, 변수의 스케일에 따라 다른 결과를 나타낼 수 있다.
유용한곳:
1> 종속변수가 없는 데이터셋에서 데이터 특성을 간단하게 살펴보는 용도
2> 마케팅이나 제품 기획 등을 목적으로 한 고객 분류
3> 지도 학습에서 종속변수를 제외하고 사용 ==> 탐색적 자료 분석 혹은 피처 엔지니어링 용도
2. K-MEAN 모델링
from sklearn.cluster import KMeans
kmeans_model = KMeans(n_clusters= 3 , random_state= 100)
#n_clusters ==> 그룹화 개수
kmeans_model.fit(data) # 학습data['label'] = kmeans_model.predict(data) # 예측
data
sns.scatterplot(x='var_1' , y='var_2' , data=data , hue='label' , palette='rainbow')
#하이퍼파라미터에 hue를 사용해 레이블별로 다른 색상 부여
2. K값 찾기_엘보우 기법
엘보우(elbow method) : 최적의 클러스터 개수를 확인하는 방법
==> 클러스터의 중점과 각 데이터 간의 거리를 기반으로 계산
==> 각 그룹에서의 중심과 각 그룹에 해당하는 데이터 간의 거리에 대한 합을 계산한다. ==> 이너셔 or 관성이라고 한다.
kmeans_model.inertia_ # 이니셔 확인3090.033
==> 이니셔값은 클러스터의 중점과 데이터 간의 거리이므로, 작을수록 그룹별로 오밀조밀 모이게 분류됐다고 할 수 있다.
==> but. 그룹의 개수(K값)이 커지면 당연히 이니셔 값 작아진다. ==> 더 좋아진다고 볼 수 없다.
distance = []
for k in range(2, 10) :
k_model = KMeans(n_clusters=k)
k_model.fit(data) # 학습
distance.append(k_model.inertia_) # 이너셔를 리스트에 저장
distance==> 각 k별 이너셔값 파악
sns.lineplot(x= range(2,10) , y= distance)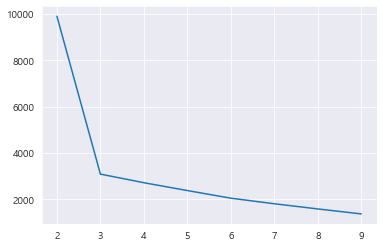
==> 확 꺾어는 x=3 지점을 포착하여 K값으로 내세운다.
3. 전처리 : 피처엔지니어링
customer_dummy = pd.get_dummies(data , columns = ['category']) # 더미 변수로 변환, 모든 범주확인 위해 drop_first= True 하지 않는다.and
customer_dummy.head()from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled_df = pd.DataFrame(scaler.fit_transform(customer_agg) , columns = customer_agg.columns, index = customer_agg.index) # 스케일링 후 데이터프레임으로 변환
scaled_df.head()==> 거리기반 알고리즘 StandardScaler를 사용하여 데이터 스케일러 실행
출처 : 데싸노트의 실전에서 통하는 머신러닝
(Golden Rabbit , 저자 : 권시현)
※혼자 공부용