annotate★IQR★boxplot★z-점수와 분위수★기초통계학-[Chapter03 - 09]
1. z-점수(표준점수_ Standardized score)
산포도 : 자료 중심위치를 나타내는 척도와 밀집 정도 또는 흩어진 정도를 나타낸다.
==> 수능을 치르게 되면 상대적인 위치 관계 이용
==> ex) 원점수, 표준점수 , 백분위 점수 ==> 3종류의 점수 부여
원점수 : 본인의 실제 점수
표준점수 & 백분위 점수 : 과목 간의 난이도에 따른 점수의 차이 보정 위한 상대적 의미의 점수
==> 자료 집단을 구성하는 자료 값들의 상대적인 위치 나타내는 척도 => 개개의 자료값이 평균으로부터 얼마나 멀리 떨어져 있는가 파악하는데 도움
모집단의 z-점수

표본의 z-점수

EX) z-점수가 1.5인 실제 자료 값은 평균보다 표준편차의 1.5배 만큼 큰 위치의 자료 값
==>z-점수가 양수이면 실제 자료 값은 평균보다 크고, 음수이면 실제 자료 값이 평균보다 작다.
A = [90,85,75,77,83]
MEAN = np.mean(A)
STD = np.std(A , ddof =1)
print(STD)
A = pd.DataFrame(A)
A.describe()==> ddof =1 로 설정!!!



A = A.rename(columns = {0 : 'x_i'})
A['x_i - |x'] = A['x_i'] - MEAN
A['z_i = (x_i - |x)/ s'] = A['x_i - |x'] / STD
A
EX) 2562명 응시자 평균 : 555점 , 표준편차 : 68점
A 점수 : 562점
B 점수 : 549점
|x = 555 s = 68
A = [562 , 549]
A = pd.DataFrame(A)
A['Z-SCORE'] = (A[0] - 555) / 68
A

2. 사분위수 & 백분위수
==> 중위수 : 자료를 작은 수에서 크기순으로 나열하여 한가운데에 놓이는 수를 중위수
n개의 자료로 구성된 자료 집단을 크기순으로 나열 ==> k개의 부분집단으로 등분하는 척도 ==> 분위수(fractiles)
사분위수(Quartiles) : 크기순으로 나열된 자료 집단을 4등분
백분위수(Percentile): 자료집단을 100등분하는 척도
1. 자료값을 가장 작은 수부터 크기순으로 나열
2. m = k*n / 100
3. m이 정수인 경우 Pk는 m번째와 (m+1) 번째 위치하는 자료 값의 평균
EX)
A = [67,84,79,62,78,36,38,57,48,87,83,90,60,25,50,94,60,62,97,43]
A = sorted(A)
A==> 자료 값을 가장 작은 수 부터 나열
print(len(A))
n = len(A)
k = 30
m = n*k / 100
print(m)
P_30 = (A[5]+ A[6]) / 2 #6번째수 , 7번째수
print("30-백분위수 : {}".format(P_30)) # 30-백분위수
k = 25
m = int(n*k / 100)
P_25 = (A[m-1] + A[m]) / 2
print("25-백분위수 : {}".format(P_25)) #25-백분위수
k = 50
m = int(n*k / 100)
P_50 = (A[m-1] + A[m]) / 2
print("50-백분위수 : {}".format(P_50)) #50-백분위수
k = 75
m = int(n*k / 100)
P_75 = (A[m-1] + A[m]) / 2
print("75-백분위수 : {}".format(P_75)) #75-백분위수
30-백분위수 : 53.5
k = 30
n = 20
m = 30*20 / 100 = 6
25-백분위수 : 49.0 ==> 제 1 사분위수
50-백분위수 : 62.0 ==> 제 2 사분위수
75-백분위수 : 83.5 ==> 제 3 사분위수
EX-02)
A = [161,144,129,162,186,163,138,172,148,157,183,129,160,152,150,194,136,122,197,143,145,176,181,157,189]
A = sorted(A)
print(len(A))D
n = len(A)
k = [70, 25 ,50 ,75]
for i in k:
m = int(n*i /100)
print(m)
print("{}-백분위수 : {}".format(i, (A[m-1] + A[m]) /2))17
70-백분위수 : 167.5
m : 6
25-백분위수 : 143.5 ==> 제 1 사분위수
m : 12
50-백분위수 : 157.0 ==> 제 2 사분위수
m : 18
75-백분위수 : 174.0 ==> 제 3 사분위수
3. 상자그림(BOX PLOT)
1) 사분위수 범위
==> 사분위수 범위(Interquartile range) : 제 1사분위수에서 제 3 사분위수까지의 범위

EX) 위의 A 리스트에 대한 사분위수 범위 구하기
A = [67,84,79,62,78,36,38,57,48,87,83,90,60,25,50,94,60,62,97,43]Q1 = 49
Q3 = 83.5
사분위수 범위 : 83.5-49 = 34.5
EX-02)
A = [161,144,129,162,186,163,138,172,148,157,183,129,160,152,150,194,136,122,197,143,145,176,181,157,189]Q1= 143.5
Q3 = 174
사분위수 범위 : 174-143.5 = 30.5
2) 상자그림(box plot)
==> 1. 특이점에 대한 정보 제공
2. 자료의 흩어진 모양을 쉽게 파악
3. 두 개 이상의 자료 집단을 비교할 때 매우 유용
1> 아래쪽 안울타리(lower inner fence) :

2> 위쪽 안울타리(upper inner fence) :

3> 아래쪽 바깥 울타리(lower outer fence)

4> 위쪽 바깥 울타리(Upper outer fence)

5> 안정값(adjacent value)
==> 안울타리 안에 놓이는 가장 극단적인 자료 값, 아래쪽 안울타리보다 큰 가장 작은 자료값과 위쪽 안울타리보다 작은 가장 큰 자료값
6> 보통 특이값(mild outlier) : 안울타리와 바깥울타리 사이에 놓이는 자료값
7> 극단 특이값(extreme outlier) : 바깥울타리 외부에 놓이는 자료 값
fig = plt.figure(figsize=(15,15))
ax = sns.boxplot(data = B)
n = len(B)
k = [25,50,75] #Q1
for i in k:
m = int((n*i) / 100)
P_25 = (A[m-1] + A[m]) /2
print(P_25)
Q1 = round(B.quantile(.25)[0] , 2)
Q2 = round(B.quantile(.5)[0] , 2)
Q3 = round(B.quantile(.75)[0] , 2)
IQR = round(Q3 - Q1 , 2) #1.6
print("IQR: {}".format(IQR))
fl = round(Q1 - (1.5) * IQR ,2) #아래쪽 안 울타리
print('fl : {}'.format(fl))
fu = round(Q3 +(1.5) * IQR,2) #위쪽 안 울타리
print('fu : {}'.format(fu))
fL = round(Q1 - 3*IQR,2) #아래쪽 밖 울타리
print('fL : {}'.format(fL))
fU = round(Q3 + 3*IQR,2) #위쪽 밖 울타리
print('fU : {}'.format(fU))
print("B.quantile(0)[0] : {}".format(B.quantile(0)[0]))
print("B.quantile(1)[0] : {}".format(B.quantile(1)[0]))
print("B.quantile(.25)[0] : {}".format(B.quantile(.25)[0]))
ax.set_ylim(B.quantile(0)[0] -5, B.quantile(1)[0] +5)
ax.set_xlabel('Data Type')
plt.annotate('' , xy=(0.5, np.median(B)), xytext=(0.4 , np.median(B)) , arrowprops = dict(facecolor = 'black'))
plt.text(0.5, np.median(B), '중위값, : {}'.format(B.quantile(.5)[0]), fontsize=14)
plt.annotate('' , xy=(0.5, Q1), xytext=(0.4 , Q1) , arrowprops = dict(facecolor = 'black'))
plt.text(0.5, Q1, '제 1분위수, : {}'.format(Q1), fontsize=14 , color= 'red')
plt.annotate('' , xy=(0.5, Q3), xytext=(0.4 , Q3) , arrowprops = dict(facecolor = 'black'))
plt.text(0.5, Q3, '제 3분위수, : {}'.format(Q3), fontsize=14 , color= 'red')
plt.annotate('' , xy=(0.5, B.quantile(1)), xytext=(0.01 , B.quantile(1)) , arrowprops = dict(facecolor = 'black'))
plt.text(0.5, B.quantile(1), '인접값 , {}'.format(B.quantile(1)[0]), fontsize=14, color= 'red' )
plt.annotate('' , xy=(0.5, Q1 - IQR+0.08), xytext=(0.2 , Q1 - IQR+0.08) , arrowprops = dict(facecolor = 'black'))
plt.text(0.5, Q1 - IQR+0.08, '인접값 , {}'.format(Q1 - IQR+0.08), fontsize=14, color= 'red' ) #왜 다를까?
plt.annotate('' , xy=(0.2, B.quantile(0)), xytext=(0.01, B.quantile(0)) , arrowprops = dict(facecolor = 'black'))
plt.text(0.2, B.quantile(0), '특이값 , {}'.format(B.quantile(0)[0]), fontsize=14 , color= 'red')
plt.annotate('' , xy=(0.2, fl), xytext=(0.01, fl) , arrowprops = dict(facecolor = 'black'))
plt.text(0.2, fl, '아래쪽 안울타리의 인접값 , {}'.format(fl), fontsize=14 , color= 'red')
plt.annotate('' , xy=(0.2, fu), xytext=(0.01, fu) , arrowprops = dict(facecolor = 'black'))
plt.text(0.2, fu, '위쪽 안울타리의 인접값 , {}'.format(fu), fontsize=14 , color= 'red')
plt.annotate('' , xy=(0.2, fU), xytext=(0.01, fU) , arrowprops = dict(facecolor = 'black'))
plt.text(0.2, fU, '위쪽 밖울타리의 인접값 , {}'.format(fU), fontsize=14 , color= 'red')
plt.annotate('' , xy=(0.2, fL), xytext=(0.01, fL) , arrowprops = dict(facecolor = 'black'))
plt.text(0.2, fL, '아래쪽 밖울타리의 인접값 , {}'.format(fL), fontsize=14 , color= 'red')
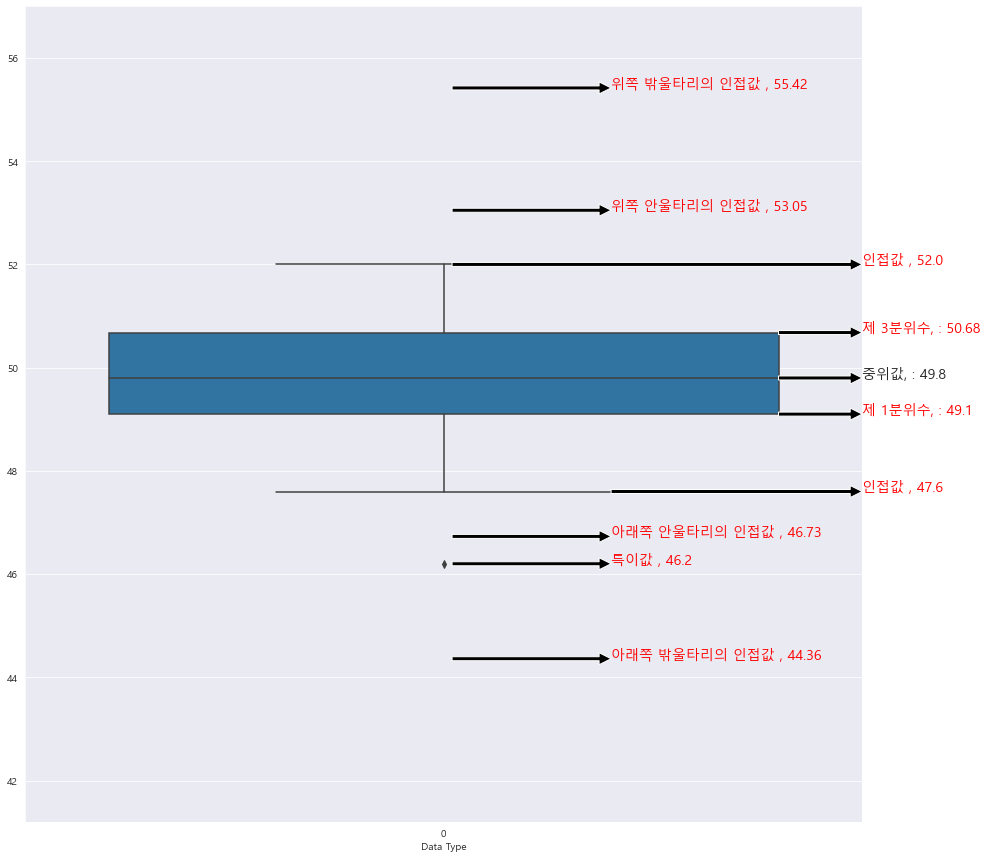
plt.show()Q1 = 49.1
Q2 = 49.8
Q3 = 50.7
IQR: 1.6
fl : 46.7 ==> 아래쪽 안 울타리
fu : 53.1 ==> 위쪽 안 울타리
fL : 44.3= ==> 아래쪽 밖 울타리
fU : 55.5 ==> 위쪽 밖 울타리
B.quantile(0)[0] : 46.2 #B의 0%값
B.quantile(1)[0] : 52.0 #B의 100% 값
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 평균,표준편차,분산' 카테고리의 다른 글
| most_common()★.join(map(str , 변수)★np.argmax★np.bincount★최빈값★기초통계학-[Chapter03 - 연습문제] (0) | 2022.12.09 |
|---|---|
| Lmport★np.cov()★공분산★상관관계(Correlation)★상관계수(Coefficient)★기초통계학-[Chapter03 - 10] (0) | 2022.12.07 |
| 변동계수★기초통계학-[Chapter03 - 08] (0) | 2022.12.07 |
| insert() , index★그룹화 자료의 분산과 표준편차★기초통계학-[Chapter03 - 07] (0) | 2022.12.07 |
| 경험적규칙★체비쇼프 정리★기초통계학-[Chapter03 - 06] (0) | 2022.12.06 |