전체 글
-
[PYTHON - 머신러닝_캐글_모델]★XGBoost★LightGBM2023.02.01
-
[PYTHON - 머신러닝_캐글_모델]★선형 회귀 모델★2023.01.31
[PYTHON - 머신러닝_캐글_실습-03]자전거 대요 수요 예측★calendar★lambda
1. 문제 : season기준이 아닌 month 기준으로 훈련 결과 값 출력
1. 데이터 전처리
import numpy as np
import pandas as pd
data_path = './bike-sharing-demand/'
train = pd.read_csv(data_path + 'train.csv') # 훈련 데이터
test = pd.read_csv(data_path + 'test.csv') # 테스트 데이터
submission = pd.read_csv(data_path + 'sampleSubmission.csv') # 제출 샘플 데이터==> train , test , submission 데이터 불러오기
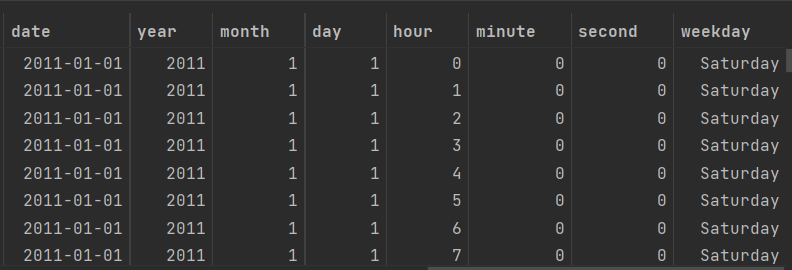
train['date'] = train['datetime'].apply(lambda x : x.split()[0]) # 날짜 피처 생성
train['datetime'] = pd.to_datetime(train['datetime'])
train['year'] = train['datetime'].dt.year # 연도
train['month'] = train['datetime'].dt.month # 월
train['day'] = train['datetime'].dt.day
train['hour'] = train['datetime'].dt.hour # 시간
train['minute'] = train['datetime'].dt.minute # 분
train['second'] = train['datetime'].dt.second # 초
train['weekday'] = train['datetime'].dt.weekday # 요일
trainimport calendar
from datetime import datetime
# train['weekday'] = train['date'].apply(lambda dateString : calendar.day_name[datetime.strptime(dateString , '%Y-%m-%d').weekday()]) # weekday 출력하기(요일)
train['weekday'] = train['weekday'].apply(lambda dateString : calendar.day_name[dateString]) # weekday 출력하기(요일)
train==> lambda 활용및 , calendar 라이브러리 활용하여 dateString의 값에 따라, 요일로 변환
mpl.rc('font' , size = 14) # 폰트 크기 설정
mpl.rc('axes' , titlesize = 15) # 각 축의 제목 크기 설정
figure , axes = plt.subplots(nrows=1 , ncols=2) # 3행 2열 Figure 생성
plt.tight_layout() # 그래프 사이에 여백 확보
figure.set_size_inches(10 , 9) # 전체 Figure 크기를 10x9 인치로 설정
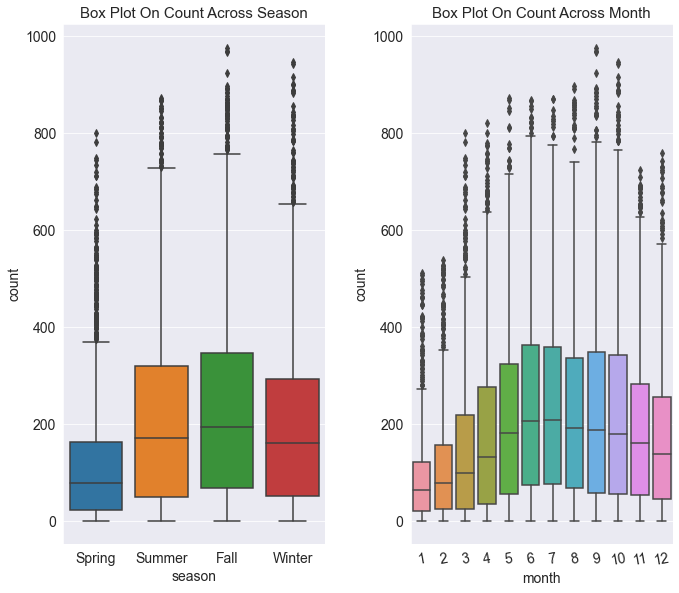
sns.boxplot(x='season' , y ='count' , data = train , ax = axes[0])
sns.boxplot(x='month' , y ='count' , data = train , ax = axes[1])
# sns.boxplot(x='workingday' , y ='count' , data = train , ax = axes[1,1])
axes[0].set(title ='Box Plot On Count Across Season')
axes[1].set(title='Box Plot On Count Across Month')
# axes[1,0].set(title='Box Plot On Count Across Holiday')
# axes[1,1].set(title='Box Plot On Count Across Workingday')
#
axes[1].tick_params(axis= 'x' , labelrotation = 10)
plt.show()==> axes[0,1] 이 아닌 axes[0] , axes[1] 로 받는다.
mpl.rc('font' , size = 11)
figure , axes = plt.subplots(nrows=2) # 5행 1열
figure.set_size_inches(12,18)
# STEP 2 : 서브플롯 할당
# 근무일 , 공휴일 , 요일 ,계절 , 날씨에 따른 시간대별 평균 대여 수량 포인트플롯
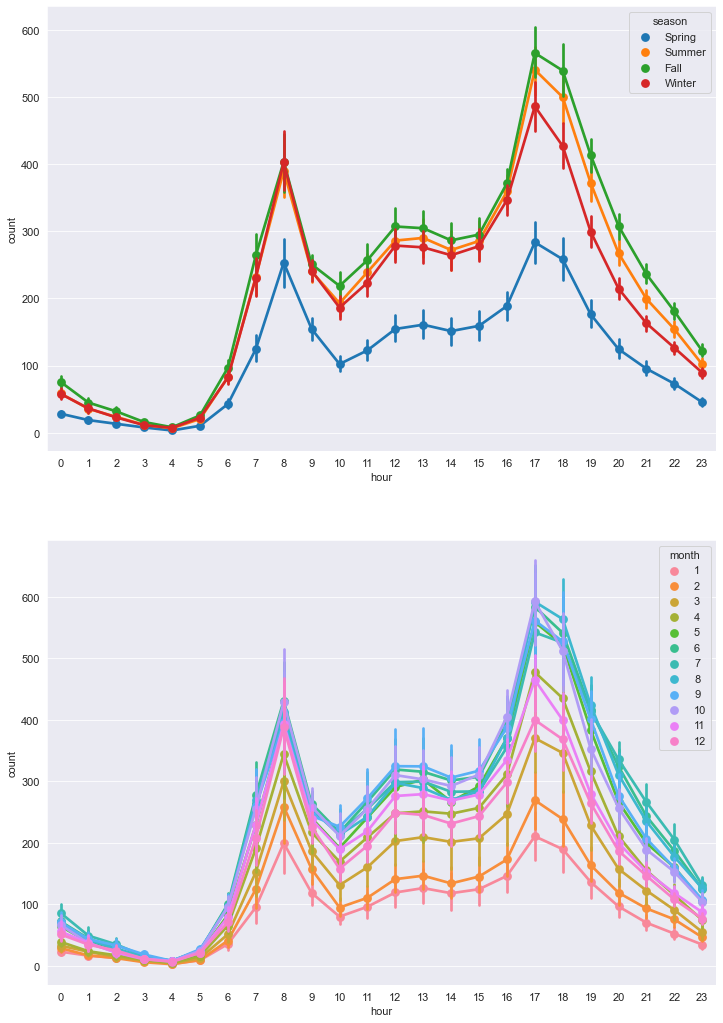
sns.pointplot(x='hour' , y='count' , data = train , hue='season' , ax= axes[0]) # hue로 비교하고 싶은 피처 전달
sns.pointplot(x='hour' , y='count' , data = train , hue='month' , ax= axes[1])
2. 모델 예측
drop_features = ['casual' , 'registered' , 'datetime' , 'date' , 'season' , 'windspeed']
all_data = all_data.drop(drop_features , axis = 1)
all_data# 훈련 데이터의 테스트 데이터 나누기
X_train = all_data[~pd.isnull(all_data['count'])] # all_data의 count 열에서 null 이 아닌 값들에 대한 모든 열
X_test = all_data[pd.isnull(all_data['count'])] # all_data 의 count열에서 null 인 값들에 대한 모든 열
X_train# 타깃값 count 제거
X_train = X_train.drop(['count'] , axis =1)
X_test = X_test.drop(['count'], axis =1)
y = train['count'] # 타깃값==> 타깃값(종속변수)에 count 값 집어넣기
import numpy as np
def rmsle(y_true , y_pred , convertExp = True):
if convertExp:
y_true = np.exp(y_true)
y_pred = np.exp(y_pred)
# 로그변환 후 결측값을 0으로 변환
log_true = np.nan_to_num(np.log(y_true +1))
log_pred = np.nan_to_num(np.log(y_pred +1))
# RMSLE 계산
output = np.sqrt(np.mean((log_true - log_pred)**2))
return output==> 모델 성능 평가
from sklearn.linear_model import LinearRegression
linear_reg_model = LinearRegression()
log_y = np.log(y) # 타깃값 로그변환
linear_reg_model.fit(X_train , log_y) # 모델 훈련preds = linear_reg_model.predict(X_train) # 코드 실행시 훈련된 선형 회귀 모델이 X_train 피처를 기반으로 타깃값을 예측
# 훈련시에는 훈련 데이터만, 검증시 검증 데이터만 , 테스트 시 테스트 데이터를 사용해야 한다.
# 지금처럼 훈련 시 사용한 데이터를 예측할 때 사용하는 경우는 없다.
# 시험 공부할 때 이미 풀어본 문제가 실제 시험에 나오면 안되는 이유와 같기 때문이다.from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestRegressor
from sklearn import metrics
# 교차검증용 평가 함수(RMSLE 점수 계산)
rmsle_scorer = metrics.make_scorer(rmsle, greater_is_better= False)
# 모델 생성
randomforest_model = RandomForestRegressor()
# 그리드서치 객체 생성
rf_params = {'random_state' : [42] , 'n_estimators' : [100, 120 ,140]} # random_state는 랜덤 시드값 , n_estimators는 랜덤 포레스트를 구성하는 결정 트리 개수
gridsearch_random_forest_model = GridSearchCV(estimator= randomforest_model , param_grid= rf_params ,
scoring = rmsle_scorer , cv=5)
# 그리드서치 수행
log_y = np.log(y)
gridsearch_random_forest_model.fit(X_train , log_y)
print('최적 하이퍼파라미터 : ' , gridsearch_random_forest_model.best_params_)==> 랜덤 포레스트 모델 실행
==> 최적 하이퍼파라미터 : {'n_estimators': 140, 'random_state': 42}
# 예측
preds = gridsearch_random_forest_model.best_estimator_.predict(X_train)
# 평가
print(f'랜덤 포레스트 회귀 RMSLE 값 : {rmsle(log_y , preds , True) : .4f}' )==> RMSLE 값 : 0.1126
import seaborn as sns
import matplotlib.pyplot as plt
randomforest_preds = gridsearch_random_forest_model.best_estimator_.predict(X_test)
fig, ax = plt.subplots(ncols=2)
fig.set_size_inches(10,4)
sns.histplot(y, bins = 50 , ax = ax[0])
ax[0].set_title('Train Data Distribution')
sns.histplot(np.exp(randomforest_preds) , bins = 50 , ax = ax[1])
ax[1].set_title('Predicted Test Data Distribution')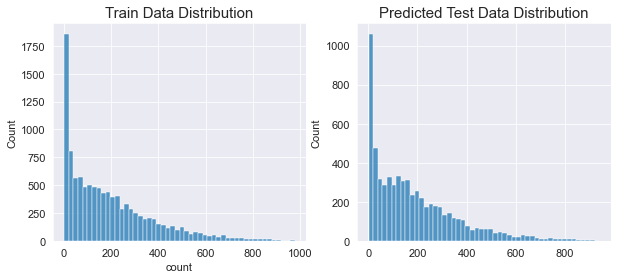
출처 : 머신러닝·딥러닝 문제해결 전략
(Golden Rabbit , 저자 : 신백균)
※혼자 공부용
'머신러닝 > 캐글_실습' 카테고리의 다른 글
[PYTHON - 머신러닝_캐글_실습-02]자전거 대요 수요 예측★np.nan_to_num★예측과 훈련의 의미★최적 하이퍼파라미터 찾기위한 그리드 서치
1. date , year , month , hour 로 구분하기
from datetime import datetime
# 날짜 피처 생성
all_data['date'] = all_data['datetime'].apply(lambda x : x.split()[0])
all_data['year'] = all_data['datetime'].apply(lambda x : x.split()[0].split('-')[0])
all_data['month'] = all_data['datetime'].apply(lambda x : x.split()[0].split('-')[1])
all_data['hour'] = all_data['datetime'].apply(lambda x : x.split()[1].split(':')[0])
all_data['minute'] = all_data['datetime'].apply(lambda x : x.split()[1].split(':')[1])
# 요일 피처 생성
all_data['weekday'] = all_data['date'].apply(lambda dateString : datetime.strptime(dateString, '%Y-%m-%d').weekday())
# 훈련 데이터는 매달 1~19일 , 테스트 데이터는 20일~ 말일 ==> 대여 수량을 예측할 때 day 피처는 사용할 필요가 없다.all_data['datetime'] = pd.to_datetime(all_data['datetime'])
all_data['year'] = all_data['datetime'].dt.year # 연도
all_data['month'] = all_data['datetime'].dt.month # 월
all_data['hour'] = all_data['datetime'].dt.hour # 시간
all_data['weekday'] = all_data['datetime'].dt.weekday # 요일
all_data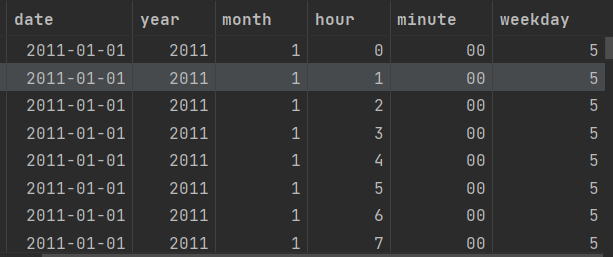
2. casual , registered , datetime ,date , month ,windspeed 삭제하기
drop_features = ['casual' , 'registered' , 'datetime' , 'date' , 'month' , 'windspeed']
all_data = all_data.drop(drop_features , axis = 1)
all_data3. 데이터 나누기
# 훈련 데이터의 테스트 데이터 나누기
X_train = all_data[~pd.isnull(all_data['count'])] # all_data의 count 열에서 null 이 아닌 값들에 대한 모든 열
X_test = all_data[pd.isnull(all_data['count'])] # all_data 의 count열에서 null 인 값들에 대한 모든 열
# 타깃값 count 제거
X_train = X_train.drop(['count'] , axis =1)
X_test = X_test.drop(['count'], axis =1)
y = train['count'] # 타깃값==> pd.isnull() 주목!!
4. 평가지표 계산 함수(RMSLE)
import numpy as np
def rmsle(y_true , y_pred , convertExp = True):
if convertExp:
y_true = np.exp(y_true)
y_pred = np.exp(y_pred)
# 로그변환 후 결측값을 0으로 변환
log_true = np.nan_to_num(np.log(y_true +1))
log_pred = np.nan_to_num(np.log(y_pred +1))
# RMSLE 계산
output = np.sqrt(np.mean((log_true - log_pred)**2))
return output==> 지수 변환하는 이유는 타깃값으로 count가 아닌 log(count)를 사용하기 때문이다. 예측한 log(count)에 지수 변환을 하면 count를 구할 수 있다.
==> np.nan_to_num 함수는 NaN 결측값을 모두 0으로 바꾸는 함수 이다.
5. 모델 훈련
1> 사이킷런의 선형 회귀모델 LinearRegression을 임포트하여 모델을 생성
from sklearn.linear_model import LinearRegression
linear_reg_model = LinearRegression()
log_y = np.log(y) # 타깃값 로그변환
linear_reg_model.fit(X_train , log_y) # 모델 훈련==> y는 타깃값인 train['count']를 할당한 변수이다.
==> 선형 회귀모델을 훈련한다는 것은 독립변수(피처)인 X_train과 종속변수(타깃값) 인 log_y에 대응하는 최적의 선형 회귀 계수를 구한다는 의미이다.
훈련의 의미 :
훈련 :

==> 독립변수 x_1 , x_2 , x_3 와 종속변수 Y를 활용하여 선형 회귀계수 쉐타를 구할 수 있다.
==> 피처(독립변수) 와 타깃값(종속변수)이 주어졌을 때 최적의 가중치(회귀계수)를 찾는 과정
예측 :

==> 쉐타 값을 아는 상태에서 새로운 독립변수 x_1 , x_2 , x_3가 주어진다면 종속변수 Y를 구할 수 있다.
==> 최적의 가중치를 아는 상태(훈련된 모델)에서 새로운 독립변수(데이터) 가 주어졌을 때 타깃값을 추정하는 과정
6. 모델 성능 검증
preds = linear_reg_model.predict(X_test)
==> 훈련시에는 훈련 데이터만, 검증시 검증 데이터만 , 테스트 시 테스트 데이터를 사용해야 한다.
==> 시험 공부할 때 이미 풀어본 문제가 실제 시험에 나오면 안되는 이유와 같기 때문이다.
linearreg_preds = linear_reg_model.predict(X_test) # 테스트 데이터로 예측
submission['count'] = np.exp(linearreg_preds) # 지수 변환
7. 성능 개선 1 : 릿지 회귀 모델
==> 릿지 회귀 모델은 L2 규제를 적용한 선형 회귀 모델이다. 규제란 모델이 훈련 데이터에 과대적합되지 않도록 해주는 방법이다.
==> 훈련 데이터에 과대적합되면 모델이 훈련 데이터에만 너무 잘 들어맞고, 테스트 데이터로는 제대로 예측하지 못한다.
1> 하이퍼파라미터 최적화
==> 그리드 서치 : 하이퍼파라미터를 격자 처럼 촘촘하게 순회하며 최적의 하이퍼파라미터 값을 찾는 기법이다.
==> 하이퍼파라미터를 적용한 모델마다 교차 검증하며 성능을 측정하여 성능이 가장 좋았을 때의 하이퍼파라미터 값을 찾는다.
from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV
from sklearn import metrics
ridge_model = Ridge()# 하이퍼파라미터 값 목록
ridge_params = {'max_iter' : [3000] , 'alpha' : [0.1 , 1, 2, 3,4, 10 ,30, 100, 200, 300 , 400 , 800, 900 , 1000]}
# 교차검증용 평가 함수(RMSLE 점수 계산)
rmsle_scorer = metrics.make_scorer(rmsle, greater_is_better= False)
# 릿지 모델은 규제를 적용한 회귀 모델이라고 한다. 릿지 모델에서 중요한 하이퍼파라미터는 alpha로 , 값이 클수록 규제 강도가 세진다.
# 적절한 규제를 적용한다면 , 즉 alpha를 적당한 크기로 하면 과대적합 문제를 개선할 수 있다.==> alpha 값(릿지 모델의 파라미터)
==> 그리드 서치는 alpha값들은 순회하며 자동 테스트해준다.
gridsearch_ridge_model = GridSearchCV(estimator=ridge_model, param_grid= ridge_params, scoring= rmsle_scorer, cv=5 )# 릿지 모델 , 값 목록 , 평가 지표 , 교차 검증 분할 수 )==> estimator : 분류 및 회귀 모델
==> param_grid : 딕셔너리 형태로 모델의 하이퍼파라미터명과 여러 하이퍼파라미터 값을 지정
==> scoring : 평가지표, 사이킷런에서 기본적인 평가지표를 문자열 형태로 제공.
==> 정확도는 accuracy , F1 점수는 f1 , ROC-AUC는 roc_auc , 재현율은 recall로 표시
==> make_scorer는 평가지표 계산 함수와 평가지표 점수가 높으면 좋은지 여부 등을 인수로 받는 교차 검증용 평가 함수이다.
==> cv : 교차 검증 분할 개수(기본 값은 5)
log_y = np.log(y) # 타깃값 로그변환
gridsearch_ridge_model.fit(X_train , log_y) # 훈련(그리드 서치)
# 코드가 일관되도록 그리드서치 객체도 모델 객체와 똑같이 fit() 메서드를 제공한다. fit()을 실행하면 객체 생성 시 param_grid에 전달된 값을 순환하면서 교차 검증으로 평가지표 점수를 계산한다. 이때 가장 좋은 성능을 보인 값을 best_params_ 속성에 저장하여 최적 값으로
# 훈련한 모델(최적 예측기)를 best_estimator_ 속성에 저장한다.print('최적 하이퍼파라미터 : ' , gridsearch_ridge_model.best_params_)preds = gridsearch_ridge_model.best_estimator_.predict(X_train)
# 평가
print(f'릿지 회귀 RMSLE 값 : , {rmsle(log_y , preds , True) : .4f}')8. 성능 개선 2 : 라쏘 회귀 모델
==> 라쏘 회귀 모델은 L1 규제를 적용한 선형 회귀 모델이다.
from sklearn.linear_model import Lasso
# 모델 생성
lasso_model = Lasso()
# 하이퍼파라미터 값 목록
lasso_alpha = 1/np.array([0.1 , 1 ,2 , 3, 4, 10 ,30 , 100 , 200 , 300 , 400 , 800 , 900, 1000])
lasso_params = {'max_iter' : [3000] , 'alpha' : lasso_alpha}
# 그리드서치(with 라쏘) 객체 생성
gridsearch_lasso_model = GridSearchCV(estimator= lasso_model , param_grid= lasso_params,
scoring = rmsle_scorer , cv=5)
# 그리드서치 수행
log_y = np.log(y)
gridsearch_lasso_model.fit(X_train , log_y)
print('최적 하이퍼파라미터 : ', gridsearch_lasso_model.best_params_)# 예측
preds = gridsearch_lasso_model.best_estimator_.predict(X_train)
# 평가
print(f'라쏘 회귀 RMSLE 값 : {rmsle(log_y , preds , True) : .4f}')9. 성능 개선 3 : 랜덤 포레스트 회귀 모델
https://knowallworld.tistory.com/376
[PYTHON - 머신러닝_랜덤 포레스트]★str.split(expand= True)★K-폴드 교차검증★하이퍼파라미터 튜닝
1. 랜덤 포레스트 ==> 결정 트리의 단점인 오버피팅 문제를 완화시켜주는 발전된 형태의 트리 모델이다. https://knowallworld.tistory.com/375 [PYTHON - 머신러닝_결정트리]★예측력, 설명력★빈칸 제거_skipin
knowallworld.tistory.com
오버피팅 : 예측 모델이 훈련 셋을 지나치게 잘 예측한다면 새로운 데이터를 예측 할 때 큰 오차를 유발 할 수 있다. ==> 훈련 셋과 테스트 셋의 예측 정확도를 줄여야 한다.
==> 랜덤으로 생성된 무수히 많은 트리를 이용하여 예측
==> 여러 모델을 활용하여 하나의 모델을 이루는 기법을 앙상블이라 부른다.
==> 앙상블 기법 : 여러 모델을 만들고 각 예측값을 투표/평균 등으로 통합하여 더 정확한 예측 도모
from sklearn.ensemble import RandomForestRegressor
# 모델 생성
randomforest_model = RandomForestRegressor()
# 그리드서치 객체 생성
rf_params = {'random_state' : [42] , 'n_estimators' : [100, 120 ,140]}
gridsearch_random_forest_model = GridSearchCV(estimator= randomforest_model , param_grid= rf_params ,
scoring = rmsle_scorer , cv=5)
# 그리드서치 수행
log_y = np.log(y)
gridsearch_random_forest_model.fit(X_train , log_y)
print('최적 하이퍼파라미터 : ' , gridsearch_random_forest_model.best_params_)==> random_state는 랜덤 시드값 , n_estimators는 랜덤 포레스트를 구성하는 결정 트리 개수
10. 최종결과
import seaborn as sns
import matplotlib.pyplot as plt
randomforest_preds = gridsearch_random_forest_model.best_estimator_.predict(X_test)
fig, ax = plt.subplots(ncols=2)
fig.set_size_inches(10,4)
sns.histplot(y, bins = 50 , ax = ax[0])
ax[0].set_title('Train Data Distribution')
sns.histplot(np.exp(randomforest_preds) , bins = 50 , ax = ax[1])
ax[1].set_title('Predicted Test Data Distribution')==> log 변환하였으므로, exp로 지수변환 해준다.

출처 : 머신러닝·딥러닝 문제해결 전략
(Golden Rabbit , 저자 : 신백균)
※혼자 공부용
'머신러닝 > 캐글_실습' 카테고리의 다른 글
[PYTHON - 머신러닝_캐글_실습]자전거 대요 수요 예측★datetime★weekday()★calendar★map 변환★로그변환★subplots★히트맵★회귀선_regplot()★pointplot★
1. 미션
날짜, 계절 ,근무일 여부 , 날씨 , 온도, 체감 온도, 풍속 데이터를 활용하여 자전거 대여 수요 예측
2. 피처와 타깃값
피처(feature) : 원하는 값을 예측하기 위해 활요하는 데이터 ==> 열(column) 의미
타깃값(target value) : 예측해야 할 값 ==> 목표값 , 목표변수, 타깃변수
3. 날짜 변환
from datetime import datetime
import calendar
print(train['date'][100]) # 날짜
print(datetime.strptime(train['date'][100] , '%Y-%m-%d')) # datetime 타입으로 변경
# 정수로 요일 변환
print(datetime.strptime(train['date'][100] , '%Y-%m-%d').weekday())
# 문자열로 요일 변환
print(calendar.day_name[datetime.strptime(train['date'][100] , '%Y-%m-%d').weekday()])==> datetime.strptime() ==> datetime 타입으로 변경

4. map 활용하여 DataFrame 값들 변환
train['season'] = train['season'].map({1 : 'Spring' , 2: 'Summer' , 3:'Fall' , 4:'Winter'})
train['weather'] = train['weather'].map({1 : 'Clear' , 2 : 'Mist , Few clouds' , 3: 'Light Snow , Rain , Thunderstorm' , 4 : 'Heavy Rain , Thunderstorm , Snow , Fog'})
train[['season' , 'weather']]
5. 로그 변환
mpl.rc('font' , size = 15) # 폰트 크기를 15로 설정
sns.displot(train['count'])
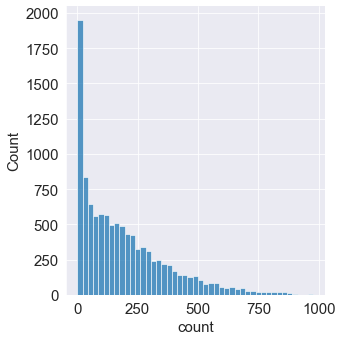
==> x축은 타깃값인 count를 나타내고, y축은 총 개수를 나타낸다. 분포도를 보면 타깃값인 count가 0 근처에 몰려 있다.
==> 분포가 왼쪽으로 많이 편향되어 있어 회귀 모델이 좋은 성능을 내려면 데이터가 정규분포를 따라야만 한다.
==> 이를 그대로 사용하여 모델링한다면 좋은 성능을 기대하기 어렵다.
==> 데이터 분포를 정규분포에 가깝게 만들기 위해 가장 많이 사용되는 방법은 로그변환이다. 로그 변환은 count 분포와 같이 데이터가 왼쪽으로 편향되어 있을 때 사용한다.
sns.displot(np.log(train['count'])) # 변환 전보다 정규분포에 가까워졌다. 타깃값 분포가 정규분포에 가까울 수록 회귀 모델 성능이 좋다.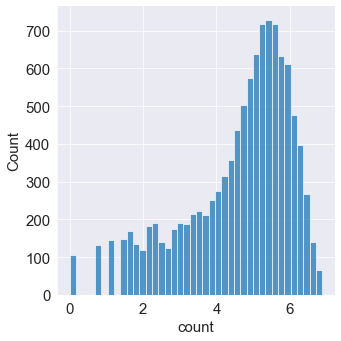
==> 마지막에는 지수변환하여 count로 복원해야만 한다!!!
6. subplots 여러개 그래프 그리기!!!
mpl.rc('font' , size = 14) # 폰트 크기 설정
mpl.rc('axes' , titlesize = 15) # 각 축의 제목 크기 설정
figure , axes = plt.subplots(nrows = 3 , ncols= 2) # 3행 2열 Figure 생성
plt.tight_layout() # 그래프 사이에 여백 확보
figure.set_size_inches(10 , 9) # 전체 Figure 크기를 10x9 인치로 설정https://knowallworld.tistory.com/244
★Seaborn에서의 Subplots★이항확률의 근사 확률★푸아송분포★기초통계학-[Chapter05 - 이산확률분포
1. 이항확률의 근사 확률 ==> 시행 횟수 n이 30보다 큰 경우의 이항확률을 구하기 위한 푸아송 분포 이용한 근사 확률 구할 수 있다. ==> 충분히 큰 n에 대햐여 np =뮤 가 일종하면 B(n ,p ) ~~ P(뮤)이므
knowallworld.tistory.com
==> 여러개 그래프 그리기

==> 객체 6개가 3행 2열로 구성된 배열이 출력되었다.
plt.tight_layout() # 그래프 사이에 여백 확보==> 그래프 사이에 여백 확보
axes[1,0].tick_params(axis= 'x' , labelrotation = 90)
axes[1,1].tick_params(axis='x' , labelrotation = 90)==> x축 라벨 회전
7. 막대그래프 , barplot
mpl.rc('font' , size = 14) # 폰트 크기 설정
mpl.rc('axes' , titlesize = 15) # 각 축의 제목 크기 설정
figure , axes = plt.subplots(nrows = 3 , ncols= 2) # 3행 2열 Figure 생성
plt.tight_layout() # 그래프 사이에 여백 확보
figure.set_size_inches(10 , 9) # 전체 Figure 크기를 10x9 인치로 설정
sns.barplot(x='year' , y ='count' , data = train , ax = axes[0,0])
sns.barplot(x='month' , y ='count' , data = train , ax = axes[0,1])
sns.barplot(x='day' , y ='count' , data = train , ax = axes[1,0])
sns.barplot(x='hour' , y ='count' , data = train , ax = axes[1,1])
sns.barplot(x='minute' , y ='count' , data = train , ax = axes[2,0])
sns.barplot(x='second' , y ='count' , data = train , ax = axes[2,1])
axes[0,0].set(title ='Rental amounts by year')
axes[0,1].set(title='Rental amounts by month')
axes[1,0].set(title='Rental amounts by day')
axes[1,1].set(title='Rental amounts by hour')
axes[2,1].set(title='Rental amounts by minute')
axes[2,1].set(title='Rental amounts by second')
axes[1,0].tick_params(axis= 'x' , labelrotation = 90)
axes[1,1].tick_params(axis='x' , labelrotation = 90)
plt.show()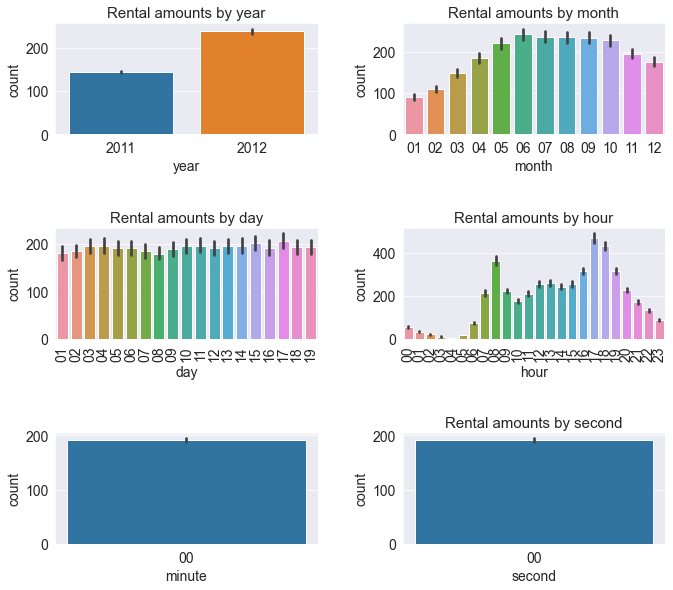
8. 박스 플롯 , boxplot
==> 박스플롯은 범주형 데이터에 따른 수치형 데이터 정보를 나타내는 그래프이다. 막대 그래프보다 더 많은 정보를 제공하는 특징이 있다.
==> 계절, 날씨 , 공휴일 , 근무일(범주형 데이터)별 대여 수량(수치형 데이터)을 박스플롯으로 그리기.
mpl.rc('font' , size = 14) # 폰트 크기 설정
mpl.rc('axes' , titlesize = 15) # 각 축의 제목 크기 설정
figure , axes = plt.subplots(nrows = 2 , ncols= 2) # 3행 2열 Figure 생성
plt.tight_layout() # 그래프 사이에 여백 확보
figure.set_size_inches(10 , 9) # 전체 Figure 크기를 10x9 인치로 설정
sns.boxplot(x='season' , y ='count' , data = train , ax = axes[0,0])
sns.boxplot(x='weather' , y ='count' , data = train , ax = axes[0,1])
sns.boxplot(x='holiday' , y ='count' , data = train , ax = axes[1,0])
sns.boxplot(x='workingday' , y ='count' , data = train , ax = axes[1,1])
axes[0,0].set(title ='Box Plot On Count Across Season')
axes[0,1].set(title='Box Plot On Count Across Weather')
axes[1,0].set(title='Box Plot On Count Across Holiday')
axes[1,1].set(title='Box Plot On Count Across Workingday')
#
axes[0,1].tick_params(axis= 'x' , labelrotation = 10)
plt.show()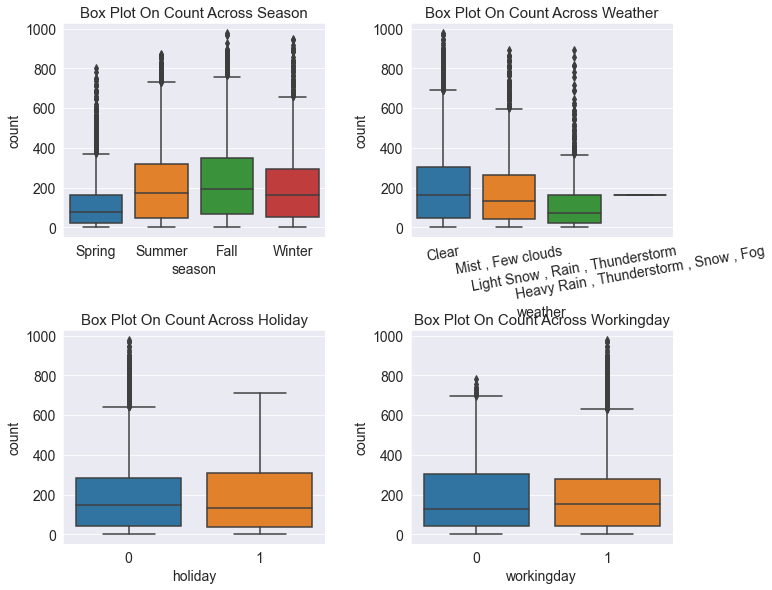
https://knowallworld.tistory.com/220
annotate★IQR★boxplot★z-점수와 분위수★기초통계학-[Chapter03 - 09]
1. z-점수(표준점수_ Standardized score) 산포도 : 자료 중심위치를 나타내는 척도와 밀집 정도 또는 흩어진 정도를 나타낸다. ==> 수능을 치르게 되면 상대적인 위치 관계 이용 ==> ex) 원점수, 표준점수
knowallworld.tistory.com
==> 자전거 대여 수량은 봄에 가장 적고, 가을에 가장 많다.
==> 날씨로는 화창할때 가장 많다.
==> 공휴일이 아닐때(0) 보다 공휴일(1) 일때 갯수가 조금 많다. 공휴일 아닐때 이상치값이 많다.
==> 근무일 일때 이상치값이 많다.
9. 포인트 플롯 , pointplot
mpl.rc('font' , size = 11)
figure , axes = plt.subplots(nrows=5) # 5행 1열
figure.set_size_inches(12,18)
# STEP 2 : 서브플롯 할당
# 근무일 , 공휴일 , 요일 ,계절 , 날씨에 따른 시간대별 평균 대여 수량 포인트플롯
sns.pointplot(x='hour' , y='count' , data = train , hue='workingday' , ax= axes[0]) # hue로 비교하고 싶은 피처 전달
sns.pointplot(x='hour' , y='count' , data = train , hue='holiday' , ax= axes[1])
sns.pointplot(x='hour' , y='count' , data = train , hue='weekday' , ax= axes[2])
sns.pointplot(x='hour' , y='count' , data = train , hue='season' , ax= axes[3])
sns.pointplot(x='hour' , y='count' , data = train , hue='weather' , ax= axes[4])
==> hue로 비교하고 싶은 피처 전달

==> 출퇴근 시간에 대여 수량이 많고, 쉬는 날에는 오후 12~2시에 가장 많다.
==> 공휴일, 요일에 따른 포인트 플롯도 근무일 여부에 다른 포인트플롯과 비슷하다.
==> 계절로는 가을에 가장 많고, 봄에 가장 적다.
==> 맑을때가 가장 많고, 폭우 폭설이 내릴때 18시에 대여 건수가 존재한다. ==> 이상치 데이터로써 제거하는 편이 좋다.
10. 회귀선을 포함한 산점도 그래프
==> 수치형 데이터인 온도, 체감 온도 , 풍속 , 습도별 대여 수량을 '회귀선을 포함한 산점도 그래프' 로 그리기.
mpl.rc('font' , size = 15)
figure, axes = plt.subplots(nrows = 2 , ncols =2) # 2행 2열
plt.tight_layout()
figure.set_size_inches(7,6)
#STEP 2 : 서브플롯 할당
# 온도, 체감온도 , 풍속, 습도 별 대여 수량 산점도 그래프
sns.regplot(x = 'temp' , y='count' , data= train, ax= axes[0,0] , scatter_kws= {'alpha' : 0.2} , line_kws={'color' : 'blue'})
# scatter_kws는 산점도 그래프의 점의 투명도를 조절한다.
sns.regplot(x = 'atemp' , y='count' , data= train, ax= axes[0,1] , scatter_kws= {'alpha' : 0.2} , line_kws={'color' : 'blue'})
sns.regplot(x = 'windspeed' , y='count' , data= train, ax= axes[1,0] , scatter_kws= {'alpha' : 0.2} , line_kws={'color' : 'blue'})
sns.regplot(x = 'humidity' , y='count' , data= train, ax= axes[1,1] , scatter_kws= {'alpha' : 0.2} , line_kws={'color' : 'blue'})
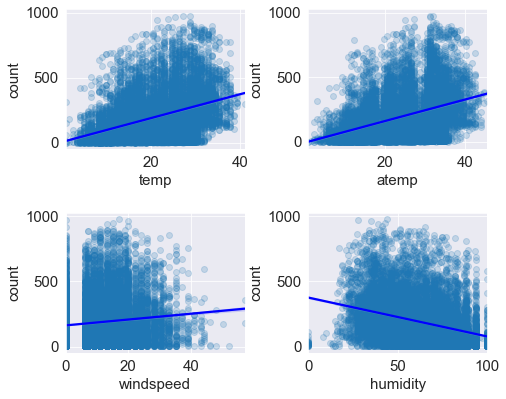
==> 온도가 높을 수록 대여 수량이 많다.
==> 습도는 낮을수록 대여를 많이 한다.
==> 풍속이 셀수록 대여 수량이 많다(?) ==> windspeed에 결측값이 많아 풍속이 0인 데이터가 많은 것 ==> 전처리 필요
11. 히트맵
==> 수치형 데이터(temp, atemp , humidity, windspeed , count) 의 상관관계 파악
train[['temp' , 'atemp' , 'humidity' , 'windspeed' , 'count']].corr()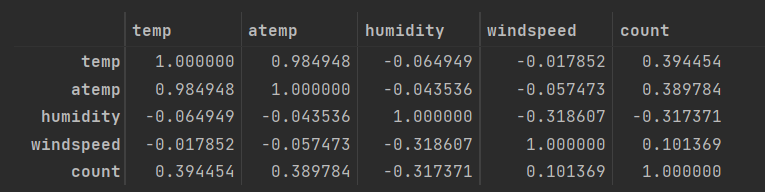
corrMat = train[['temp' , 'atemp' , 'humidity' , 'windspeed' , 'count']].corr()
fig , ax = plt.subplots()
fig.set_size_inches(10,10)
sns.heatmap(corrMat , annot = True)
ax.set(title = 'Heatmap of Numerical Data')==> annot = True 로 상관계수 값 안에 집어 넣는다.
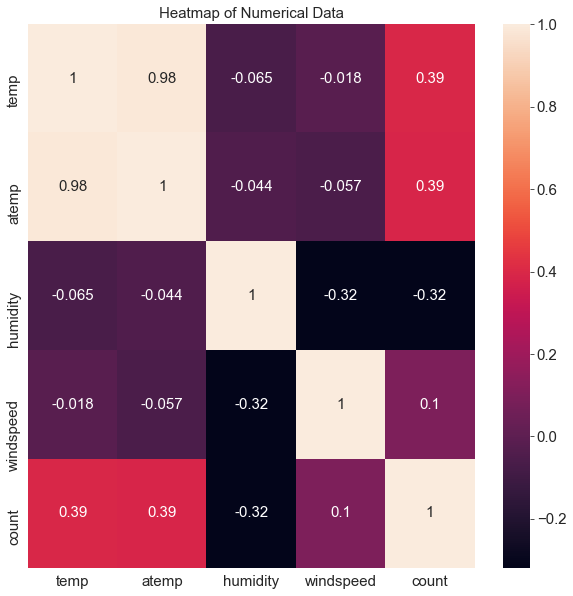
==> 온도가 높을 수록 대여 수량이 많다.
==> 습도와 대여 수량은 음수이니 습도가 '낮을 수록' 대여 수량이 많다.
출처 : 머신러닝·딥러닝 문제해결 전략
(Golden Rabbit , 저자 : 신백균)
※혼자 공부용
'머신러닝 > 캐글_실습' 카테고리의 다른 글
[PYTHON - 머신러닝_캐글_모델]★하이퍼파라미터 최적화★그리드 서치★랜덤서치★베이지안 최적화★
1. 하이퍼파라미터
==> 하이퍼파라미터는 사용자가 직접 설정해야 하는 값이다.
==> 모델이 좋은 성능을 내려면 하이퍼파라미터가 어떤 값을 가지면 좋을지를 찾는 작업이 하리어파라미터 최적화 이다.
2. 그리드 서치
==> 그리드서치는 가장 기본적인 하이퍼파라미터 최적화 기법
==> 주어진 하이퍼파라미터를 모두 순회하며 가장 좋은 성능을 내는 값을 찾는다. ==> 모든 경우의 수를 탐색
3. 랜덤 서치
==> 하이퍼파라미터를 무작위로 탐색해 가장 좋은 성능을 내는 값을 찾는 기법
==> 무작위라는 한계 때문에 그리드 서치나 베이지안 최적화에 비해 사용 빈도가 떨어진다.
4. 베이지안 최적화(bayesian optimiziation)
==> 사전 정보를 바탕으로 최적 하이퍼파라미터 값을 확률적으로 추정하며 탐색하는 기법
==> 그리드서치나 랜덤서치보다 최적 하이퍼파라미터를 더 빠르고 효과적으로 찾는다.
1. 하이퍼파라미터 탐색 범위 설정 : 최적 값을 찾고 싶은 하이퍼파라미터의 범위 설정
2. 평가지표 계산 함수(성능 평가 함수) 정의 : 탐색하려는 하이퍼파라미터를 인수로 받아 평가지표 값을 계산해주는 함수를 정의
3. BayesianOptimization 객체 생성 : bayes_opt 패키지의 BayesianOptimization 객체를 생성한다. 객체 생성 시 '평가지표 계산 함수'와 '하이퍼파라미터 탐색 범위'를 입력받는다.
4. 베이지안 최적화 수행 : 하이퍼파라미터 범위 내 값을 평가지표 계산 함수에 전달하면서 평가지표 값을 구한다. 평가지표 값이 가장 좋았을 때의 하이퍼파라미터 값을 최적 하이퍼파라미터로 간주한다.
출처 : 머신러닝·딥러닝 문제해결 전략
(Golden Rabbit , 저자 : 신백균)
※혼자 공부용
'머신러닝 > 캐글_머신러닝_이론' 카테고리의 다른 글
| [PYTHON - 머신러닝_캐글_모델]★XGBoost★LightGBM (0) | 2023.02.01 |
|---|---|
| [PYTHON - 머신러닝_캐글_모델]★결정 트리★엔트로피★앙상블 학습★보팅★배깅★부스팅★랜덤포레스트 (0) | 2023.02.01 |
| [PYTHON - 머신러닝_캐글_모델]★선형 회귀 모델★ (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_교차검증]★K-폴드 교차검증★충화 K-폴드 교차검증★folds.split(data)★ (1) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_피처 스케일링]★min-max 정규화★표준화(Standardization) (0) | 2023.01.31 |
[PYTHON - 머신러닝_캐글_모델]★XGBoost★LightGBM
1. XGBoost(Extreme gradient boosting)
==> 성능이 우수한 트리 기반 부스팅 알고리즘
https://knowallworld.tistory.com/377
[PYTHON - 머신러닝_XGBoost]★pd.options.display.max_columns★정밀도, 재현율, F1-score
1. 부스팅 알고리즘 ==> 랜덤 포레스트는 각 트리를 독립적으로 만드는 알고리즘 ==> 서로 관련 없이 생성한다. ==> 부스팅은 순차적으로 트리를 만들어 이전 트리로부터 학습한 내용이 다음 트리
knowallworld.tistory.com
부스팅 알고리즘:
==> 가중치를 활용해 분류 성능이 약한 모델을 강하게 만드는 기법
==> 배깅의 경우 결정 트리 1 과 트리 2가 서로 독립적으로 결과를 예측한 다음 보팅
==> 부스팅은 모델 간 협력이 이루어진다.
==> 이전 모델이 잘못 예측한 데이터에 가중치를 부여한다. 다음 모델은 이전 모델이 잘못 예측한 데이터(가중치가 부여된 데이터) 에 더 집중해 훈련한다.
https://knowallworld.tistory.com/388
[PYTHON - 머신러닝_캐글_모델]★결정 트리★엔트로피★앙상블 학습★보팅★배깅★부스팅★랜덤
1. 결정트리(Decision tree) ==> 분류와 회귀 문제에 모두 사용 가능한 모델 ==> 머신러닝에서 결정 트리는 노드 내 데이터의 불순도를 최소화하는 방향으로 분할 한다. 불순도는 한 범주 안에 서로 다
knowallworld.tistory.com
==> 랜덤 포레스트는 결정 트리를 병렬로 배치 , XGBoost는 직렬로 배치
==> 랜덤 포레스트는 배깅방식, XGBoost는 부스팅 방식
==> 직전 트리가 예측한 값을 다음 트리가 활용해서 예측값을 조금씩 수정한다.
2. LightGBM
==> XGBoost보다 훈련 속도가 더 빠른 모델이다.
==> 대부분의 트리 기반 모델은 트리를 균형 있게 분할하며 훈련해야 트리 깊이가 최소화 되고, 과대적합도 방지한다.
==> but. 균형을 유지하려면 추가 연산이 필요하여 시간이 더 걸린다.
==> LightGBM은 말단 노드 중심으로 예측 오류를 최소화하게끔 분할.
==> BUT. 데이터 개수가 적을 때는 과대적합되기 쉬우므로 하이퍼파라미터를 조정해주어야 한다.
https://knowallworld.tistory.com/378
[PYTHON - 머신러닝_LightGBM]★geopy.distance이용한 거리계산★groupby★agg활용한 통계계산★time 라이브
1. LightGBM ==> XGBoost 이후 나온 최신 부스팅 모델. ==> 리프 중심 트리 분할 방식 사용 장점 : ㉠ XGBoost보다 빠르고 높은 정확도를 보여준다. ㉡ 예측에 영향을 미친 변수의 중요도를 확인할 수 있다.
knowallworld.tistory.com
장점 :
㉠ XGBoost보다 빠르고 높은 정확도를 보여준다.
㉡ 예측에 영향을 미친 변수의 중요도를 확인할 수 있다.
㉢ 변수 종류가 많고 데이터가 클 수록 상대적으로 뛰어난 성능을 보여준다.
단점 :
㉠ 복잡한 모델인 만큼 ,해석에 어려움이 있다.
㉡ 하이퍼파라미터 튜닝이 까다롭다.
출처 : 머신러닝·딥러닝 문제해결 전략
(Golden Rabbit , 저자 : 신백균)
※혼자 공부용
'머신러닝 > 캐글_머신러닝_이론' 카테고리의 다른 글
| [PYTHON - 머신러닝_캐글_모델]★하이퍼파라미터 최적화★그리드 서치★랜덤서치★베이지안 최적화★ (0) | 2023.02.01 |
|---|---|
| [PYTHON - 머신러닝_캐글_모델]★결정 트리★엔트로피★앙상블 학습★보팅★배깅★부스팅★랜덤포레스트 (0) | 2023.02.01 |
| [PYTHON - 머신러닝_캐글_모델]★선형 회귀 모델★ (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_교차검증]★K-폴드 교차검증★충화 K-폴드 교차검증★folds.split(data)★ (1) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_피처 스케일링]★min-max 정규화★표준화(Standardization) (0) | 2023.01.31 |
[PYTHON - 머신러닝_캐글_모델]★결정 트리★엔트로피★앙상블 학습★보팅★배깅★부스팅★랜덤포레스트
1. 결정트리(Decision tree)
==> 분류와 회귀 문제에 모두 사용 가능한 모델
==> 머신러닝에서 결정 트리는 노드 내 데이터의 불순도를 최소화하는 방향으로 분할 한다.
불순도는 한 범주 안에 서로 다른 데이터가 얼마나 섞여 있는지를 나타내는 정도
1> 엔트로피
==> 불확실한 정도, 한 범주에 데이터가 한 종류만 있다면 엔트로피는 0이된다.
==> 어떤 데이터를 고르든 그 종류를 확실하게 말할 수 있기 때문이다.
==> 서로 다른 데이터의 비율이 비등해질수록 엔트로피는 1에 가까워진다.
==> 엔트로피 값이 클수록 불순도가 높고, 작을수록 불순도도 낮다.
2> 정보 이득
==> 결정 트리는 정보 이득을 최대화하는 방향(엔트로피를 최소화 하는 방향)으로 노드를 분할한다.
3> 지니 불순도
==> 엔트로피와 유사, 지니 불순도 값이 클수록 불순도도 높고, 작을수록 불순도도 낮다.
2. 결정트리 구현(Decision tree)
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
# 유방암 데이터셋 불러오기
cancer_data = load_breast_cancer()
# 훈련, 테스트 , 데이터로 분리
X_train , X_test, y_train, y_test = train_test_split(cancer_data['data'] , cancer_data['target'] , stratify= cancer_data['target'] , test_size=0.4 , random_state= 42)
decisiontree = DecisionTreeClassifier(random_state= 42) # 결정 트리 정의
decisiontree.fit(X_train , y_train) # 모델 훈련
accuracy = decisiontree.score(X_test , y_test) # 정확도 측정
# 테스트 데이터를 활용하여 결정 트리 모델 정확도 출력
print(f'결정 트리 정확도 : {accuracy : .3f}')==> 정확도 : 0.930
3. 앙상블 학습
==> 문제를 풀 때 한 명이 푸는 것보다 여러 명이 풀어서 서로 비교해보는것이 좋다.
==> 다양한 모델이 내린 예측 결과를 결합하는 기법을 앙상블 학습이라고 한다.
1> 보팅(Voting)
㉠ 하드 보팅(hard voting) : 다수결 투표 방식으로 최종 예측값 정한다.
㉡ 소프트 보팅(soft voting) : 개별 예측 확률들의 평균을 최종 예측확률로 정한다.
2> 배깅(bagging) : 봉지(가방 등) 에 담다
==> 개별 모델로 예측한 결과를 결합해 최종 예측을 정하는 기법
==> 개별 모델이 서로 다른 샘플링 데이터를 활용
==> 대표적인 모델 : 랜덤 포레스트
https://knowallworld.tistory.com/376
[PYTHON - 머신러닝_랜덤 포레스트]★str.split(expand= True)★K-폴드 교차검증★하이퍼파라미터 튜닝
1. 랜덤 포레스트 ==> 결정 트리의 단점인 오버피팅 문제를 완화시켜주는 발전된 형태의 트리 모델이다. https://knowallworld.tistory.com/375 [PYTHON - 머신러닝_결정트리]★예측력, 설명력★빈칸 제거_skipin
knowallworld.tistory.com
㉠ 전체 훈련 데이터셋에서 무작위 샘플링한 데이터로 개별 모델을 훈련
㉡ 훈련된 개별 모델로 결과를 예측
㉢ 개별 모델의 수만큼 반복
㉣ 각 모델이 예측한 값들을 보팅하여 최종 예측값을 구한다.
3> 부스팅(boosting) : 복돋우다
==> 가중치를 활용해 분류 성능이 약한 모델을 강하게 만드는 기법
==> 배깅의 경우 결정 트리 1 과 트리 2가 서로 독립적으로 결과를 예측한 다음 보팅
==> 부스팅은 모델 간 협력이 이루어진다.
==> 이전 모델이 잘못 예측한 데이터에 가중치를 부여한다. 다음 모델은 이전 모델이 잘못 예측한 데이터(가중치가 부여된 데이터) 에 더 집중해 훈련한다.
EX)
1. '+' 와 '-' 로 구성된 원본 데이터셋
2. 모든 데이터에 동일한 가중치 부여
3. 분류 모델 1로 '+'와 '-'를 분류
4. 분류 모델 1이 잘못 분류한 데이터에 높은 가중치 부여
5. 분류 모델 2는 가중치가 부여된 데이터에 집중해 데이터를 분류
6. 분류 모델 2가 잘못 분류한 데이터에 더욱 높은 가중치 부여
7. 분류 모델 3는 이전 단계에서 가중치가 부여된 데이터에 집중해 데이터를 분류한다.
4. 랜덤 포레스트
==> 결정 트리를 배깅 방식으로 결합한 모델
==> 나무가 모여 숲을 이루듯 결정 트리가 모여 랜덤 포레스트를 구성한다.
==> 결정트리와 마찬가지로 분류, 회귀 문제에 모두 적용가능
1. 훈련 데이터셋 ==> 샘플링(복원추출) 훈련 데이터셋 A 생성
https://knowallworld.tistory.com/230
복원, 비복원 추출★SET활용하여 차집합,여집합 가능!★기초통계학-[Chapter04 - 경우의 수-03]
1. 복원추출(Replacement) ==> 표본공간에서 표본점을 선택할 때 , 동일한 표본점이 1번이상 반복하여 추출되도록 허용 EX) 1~5까지의 숫자가 적힌 공이 들어 있는 주머니에서 차례대로 2개의 공 꺼내기
knowallworld.tistory.com
==> 복원추출
2 . 결정 트리 A는 훈련 데이터셋 A를 활용해 훈련
3. 테스트 데이터로 예측해서 스팸일 확률과 일반 메일일 확률 구한다.
4. 다른 결정 트리들도 훈련과 예측을 반복
==> 각 결정 트리에서 사용하는 데이터는 전체 훈련 데이터에서 각자 샘플링 ==> 각 결정 트리마다 훈련 데이터 샘플이 다르다.
5. 각 결정트리로부터 구한 예측 확률의 평균을 구한다.
6. 결정 트리를 배깅 방식으로 결합하여 랜덤 포레스트 구성
5. 랜덤 포레스트 구현
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
# 유방암 데이터셋 불러오기
cancer_data = load_breast_cancer()
# 훈련, 테스트 데이터로 분리
X_train , X_test , y_train , y_test = train_test_split(cancer_data['data'] , cancer_data['target'] , stratify=cancer_data['target'] , test_size= 0.4 , random_state= 42) # stratify 는 층화 추출
randomforest = RandomForestClassifier(random_state= 42) # 랜덤 포레스트 정의
randomforest.fit(X_train , y_train) # 모델 훈련
accuracy = randomforest.score(X_test , y_test) # 정확도 측정
# 테스트 데이터를 활용하여 랜덤 포레스트 모델 정확도 출력
print(f'랜덤 포레스트 정확도 : {accuracy : .3f}')랜덤 포레스트 정확도 : 0.939 ==> 결정트리보다 더 높아 졌다.
출처 : 머신러닝·딥러닝 문제해결 전략
(Golden Rabbit , 저자 : 신백균)
※혼자 공부용
'머신러닝 > 캐글_머신러닝_이론' 카테고리의 다른 글
| [PYTHON - 머신러닝_캐글_모델]★하이퍼파라미터 최적화★그리드 서치★랜덤서치★베이지안 최적화★ (0) | 2023.02.01 |
|---|---|
| [PYTHON - 머신러닝_캐글_모델]★XGBoost★LightGBM (0) | 2023.02.01 |
| [PYTHON - 머신러닝_캐글_모델]★선형 회귀 모델★ (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_교차검증]★K-폴드 교차검증★충화 K-폴드 교차검증★folds.split(data)★ (1) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_피처 스케일링]★min-max 정규화★표준화(Standardization) (0) | 2023.01.31 |
[PYTHON - 머신러닝_캐글_모델]★선형 회귀 모델★
1. 선형 회귀 모델(Linear Regression)
https://knowallworld.tistory.com/371
[PYTHON - 머신러닝_선형회귀]★선형회귀★seaborn 타원만들기★모델 평가방법 RMSE , R**2★model.coef_(
1. 선형회귀 ==> 가장 기초적인 머신러닝 모델 ==> 여러가지 데이터를 연속형 변수인 목표 변수를 예측해 내는 것이 목적이다. ==> 몸무게, 나이 , BMI, 성별 등의 데이터를 활용하여 연속형 변수를
knowallworld.tistory.com
==> 선형 회귀식을 활용한 모델이다.
==> 선형 회귀 모델을 훈련한다는 것은 훈련 데이터에 잘 맞는 모델 파라미터(회귀계수)를 찾는 것이다.
==> 여러가지 데이터를 연속형 변수인 목표 변수를 예측해 내는 것이 목적이다.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
np.random.seed(0) # 시드값 고정
w0 = 5 # y 절편
w1 = 2 # 회귀 계수(쉐타)
noise = np.random.randn(100,1) # 노이즈 , 표준 정규분포를 따르는 데이터 100개를 생성하는 코드
x = 4 * np.random.rand(100, 1) # 0~4 사이 실숫값 100개 생성
y = w1 *x + w0 + noise # y = 2x + 5 에 근사하는 데이터
plt.scatter(x,y)
from sklearn.linear_model import LinearRegression
linear_reg_model = LinearRegression() # 선형 회귀 모델
linear_reg_model.fit(x, y) # 모델 훈련
print('y절편(w0) :' , linear_reg_model.intercept_)
print('회귀계수(w1) : ' , linear_reg_model.coef_)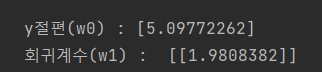
y절편값은 : intercept_
회귀계수는 : coef_
실제 y절편값 : 5 , 회귀계수값: 2 ==> 근사하게 예측하였다.
y_pred = linear_reg_model.predict(x) # 예측
plt.scatter(x,y)
plt.plot(x,y_pred) # 선형 회귀선 그리기
2. 로지스틱 선형 회귀 모델(Logistic Regression)
https://knowallworld.tistory.com/372
[PYTHON - 머신러닝_로지스틱선형회귀]★로지스틱 선형회귀★상관관계★원-핫 인코딩★정확도★
1. 로지스틱 회귀 ==> 로지스틱 회귀 또한 선형 회귀처럼 기본 분석 모델이다. ==>선형 회귀 분석은 연속된 변수를 예측하는 반면 , 로지스틱 회귀 분석은 Yes/No처럼 2가지로 나뉘는 분류 문제를 다
knowallworld.tistory.com
==> 선형 회귀 방식을 응용해 분류에 적용한 모델
==> 스팸 메일일 확률을 구하는 이진 분류 문제에 로지스틱 회귀를 사용할 수 있다.
==> 로지스틱 회귀는 시그모이드 함수를 활용해 타깃값에 포함될 확률을 예측한다.

x = np.arange(-6,6,.1)
y = 1/ (1 + np.exp(-x))
plt.plot(x,y)
이진분류 문제에선 시그모이드 값(확률)이 0.5 보다 작으면 0(음성) , 0.5보다 크면 1(양성) 이라고 예측한다.
출처 : 머신러닝·딥러닝 문제해결 전략
(Golden Rabbit , 저자 : 신백균)
※혼자 공부용
'머신러닝 > 캐글_머신러닝_이론' 카테고리의 다른 글
| [PYTHON - 머신러닝_캐글_모델]★XGBoost★LightGBM (0) | 2023.02.01 |
|---|---|
| [PYTHON - 머신러닝_캐글_모델]★결정 트리★엔트로피★앙상블 학습★보팅★배깅★부스팅★랜덤포레스트 (0) | 2023.02.01 |
| [PYTHON - 머신러닝_캐글_교차검증]★K-폴드 교차검증★충화 K-폴드 교차검증★folds.split(data)★ (1) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_피처 스케일링]★min-max 정규화★표준화(Standardization) (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_데이터 인코딩]★LabelEncoder★One-Hot-Encoder (0) | 2023.01.31 |
[PYTHON - 머신러닝_캐글_교차검증]★K-폴드 교차검증★충화 K-폴드 교차검증★folds.split(data)★
1. 교차검증
==> 일반적으로 훈련 데이터로 모델을 훈련하고, 테스트 데이터로 예측해 모델 성능을 측정한다.
==> 모델을 훈련만 하고, 성능을 검증해 보지 않으면 2가지 문제 발생
㉠ 모델이 과대적합될 가능성이 있다.
㉡ 제출 전까지 모델 성능을 확인하기 어렵다.
==> 교차 검증은 훈련 데이터를 여러 그룹으로 나누어 일부는 훈련 시 사용하고, 일부는 검증 시 사용해서 모델 성능을 측정하는 기법이다.
2. K 폴드 교차검증
https://knowallworld.tistory.com/376
[PYTHON - 머신러닝_랜덤 포레스트]★str.split(expand= True)★K-폴드 교차검증★하이퍼파라미터 튜닝
1. 랜덤 포레스트 ==> 결정 트리의 단점인 오버피팅 문제를 완화시켜주는 발전된 형태의 트리 모델이다. https://knowallworld.tistory.com/375 [PYTHON - 머신러닝_결정트리]★예측력, 설명력★빈칸 제거_skipin
knowallworld.tistory.com
데이터를 특정 개수(K개) 로 쪼개어서 그중 하나씩을 선택하여 시험셋으로 사용하되, 이 과정을 K번만큼 반복
이터레이션 1
| 훈련 셋 | 훈련 셋 | 훈련 셋 | 훈련 셋 | 시험 셋 |
이터레이션 2
| 훈련 셋 | 훈련 셋 | 훈련 셋 | 시험 셋 | 훈련 셋 |
이터레이션 3
| 훈련 셋 | 훈련 셋 | 시험 셋 | 훈련 셋 | 훈련 셋 |
이터레이션 4
| 훈련 셋 | 시험 셋 | 훈련 셋 | 훈련 셋 | 훈련 셋 |
이터레이션 5
| 시험 셋 | 훈련 셋 | 훈련 셋 | 훈련 셋 | 훈련 셋 |
==> 이터레이션(반복)은 모델링을 수행하는 단위 이다.
==> 이터레이션의 평가값(오차)의 평균값을 내어 RMSE를 도출한다.
import numpy as np
from sklearn.model_selection import KFold
data = np.array([0,1,2,3,4,5,6,7,8,9])
folds = KFold(n_splits= 5 ,shuffle= False)
for train_idx , valid_idx in folds.split(data):
print(f'훈련 데이터 : {data[train_idx]} , 검증 데이터 : {data[valid_idx]}')
folds = KFold(n_splits= 5 , shuffle= True)
for train_idx , valid_idx in folds.split(data):
print(f'훈련 데이터 : {data[train_idx]} , 검증 데이터 : {data[valid_idx]}')
3. 충화 K 폴드 교차검증(Stratified K-Fold Cross Validation)
==> 타깃값이 골고루 분포되게 폴드를 나누는 K-폴드 교차 검증 방법이다.
==> 타깃값이 불균형하게 분포되어 있는 경우 충화 K 폴드를 사용하는 것이 좋다.
EX) 일반 메일과 스펨 메일을 분류하는 문제 : 받은 메일이 1000개 , 스팸은 단 10개
==> 스팸이 10개 밖에 안되어 K 폴드 교차검증을 해도 특정 폴드에는 스팸메일이 없을 수 있다.
==> 특정 타깃값이 다른 타깃값보다 굉장히 적은 경우에 충화 K-폴드 교차검증을 사용한다.
==> 스팸 데이터를 모든 폴드에 균등하게(2개씩 , 5개 폴드) 나눈다.
y = np.array(['스팸']*5 + ['일반']*45)
# print(y)
folds = KFold(n_splits=5 , shuffle= True) # 5개의 폴드로 섞어서 출력
for idx , (train_idx , valid_idx) in enumerate(folds.split(y)):
print(f'Fold {idx+1} 검증 데이터 타깃값 : ')
print(y[valid_idx] , '\n')
==> Fold2에 스팸 메일이 없어서 스팸메일에 대한 훈련이 아예 안될 것이다.
from sklearn.model_selection import StratifiedKFold
X = np.array(range(50))
y = np.array(['스팸']*5 + ['일반'] *45)
folds = StratifiedKFold(n_splits=5) # 충화 K 폴드 교차검증
for idx , (train_idx , valid_idx) in enumerate(folds.split(X,y)): # split()에는 임의로 K개로 분할하기 때문에 피처와 타깃값 모두를 전달해야한다.
print(f'Fold {idx +1} 검증 데이터 타깃값 : ')
print(y[valid_idx] , '\n')
출처 : 머신러닝·딥러닝 문제해결 전략
(Golden Rabbit , 저자 : 신백균)
※혼자 공부용
'머신러닝 > 캐글_머신러닝_이론' 카테고리의 다른 글
| [PYTHON - 머신러닝_캐글_모델]★결정 트리★엔트로피★앙상블 학습★보팅★배깅★부스팅★랜덤포레스트 (0) | 2023.02.01 |
|---|---|
| [PYTHON - 머신러닝_캐글_모델]★선형 회귀 모델★ (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_피처 스케일링]★min-max 정규화★표준화(Standardization) (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_데이터 인코딩]★LabelEncoder★One-Hot-Encoder (0) | 2023.01.31 |
| [PYTHON - 머신러닝_캐글_분류와 회귀]★회귀 평가지표★분류 평가지표★ROC, AUC★RMSE (0) | 2023.01.31 |