1. 공분산
==> 대부분의 독립변수와 응답변수의 관계는 직선에 의하여 설명 ==> 자료점(X,Y) 가 직선에 가까우면 선형적 관계가 강하고, (x,y) 들이 직선을 중심으로 폭넓게 나타나면 선형적 관계가 약해짐.
==> 이때 이 직선을 중심으로 자료 값(x,y) 가 흩어지거나 밀집되는 정도를 나타내는 척도
==> 독립변수와 응답변수의 관계를 가짐으로써 각각의 자료가 (x,y) 형태의 쌍으로 나타나는 경우 산점도 사용
1. 모공분산(Population Covariance)
==> 독립변수의 평균편차와 응답변수의 평균편차의 곱에 대한 평균
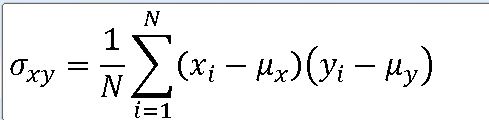
==> 뮤 x , 뮤 y 는 각각 독립변수와 응답변수의 모평균이다.
2. 표본공분산(Sample Covariance)
==> 독립변수의 평균편차와 응답변수의 평균편차의 곱을 모두 더한뒤 N-1 로 나눈 값
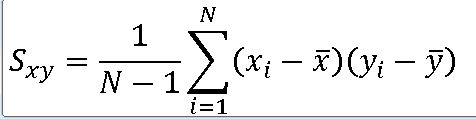
==> |x , |y 는 각각 독립변수와 응답변수의 표본평균이다.
EX-01)
A = pd.DataFrame({'월' : [21,27] , '화' : [22,28] , '수' : [22,29] , '목' : [23,30] , '금' : [23,31] , '토' : [24,32] , '일' : [24,31]})
A.index = ['최저' , '최고']
A

print(np.mean(A['최저']))
print(np.mean(A['최고']))최저의 평균 : 1.238095238095238
최고의 평균 : 3.2380952380952377
print(np.var(A['최저'] , ddof =1 ))
print(np.var(A['최고'] , ddof =1 ))최저의 분산 : 1.238095238095238
최고의 분산 : 3.2380952380952377
최저 온도와 최고 온도사이의 공분산 = 11.428571 / 6 = 1.9048
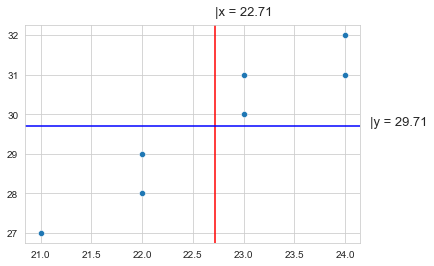
x = A.iloc[:-1, 0].tolist()
y = A.iloc[:-1 ,1].tolist()
ax = sns.set_style('whitegrid')
ax = sns.scatterplot(x= x , y = y)
ax.axvline(x= np.mean(x), ymin=0 , ymax=1 , color = 'red' , linestyle ='solid' , label ='{}'.format(2))
ax.axhline(y= np.mean(y), xmin=0 , xmax=1 , color = 'blue' , linestyle ='solid' , label ='{}'.format(2))
ax.text(np.mean(x) , 32.5 , f'|x = {round(np.mean(x),2)}',fontsize=13)
ax.text(24.25 , np.mean(y) , f'|y = {round(np.mean(y),2)}',fontsize=13)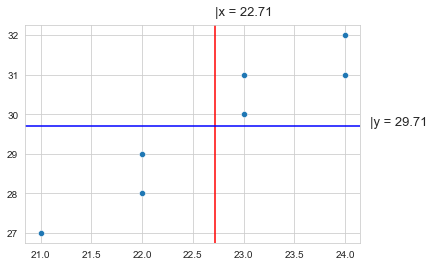
EX-02)
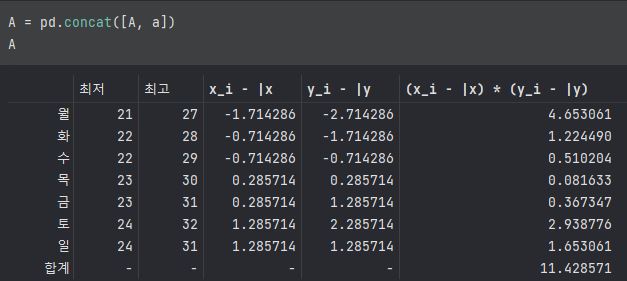
D = pd.DataFrame({'x_i' : [6,8,11,12,15] , 'y_i' : [5,7,9,9,13]})
DD['x_i - |x'] = D['x_i'] - np.mean(D['x_i'])
D['y_i - |y'] = D['y_i'] - np.mean(D['y_i'])
D['x_i - |x * y_i - |y'] = D['x_i - |x'] * D['y_i - |y']
D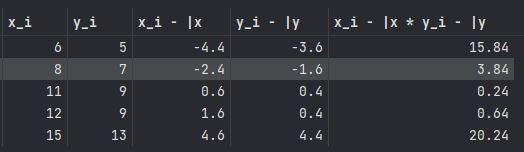
a = pd.DataFrame(D[:].sum(axis=0))
a = a.transpose()
a.index = ['합계']
a[a.columns[2:-1]] = '-'
D = pd.concat([D,a])
D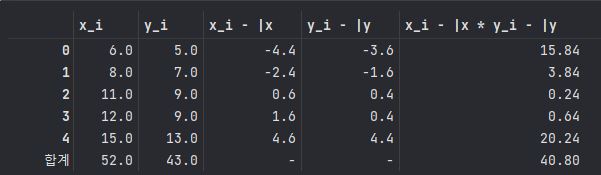
표본공분산 :
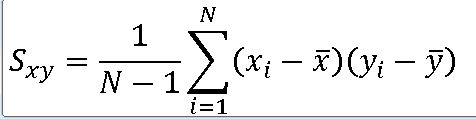
print(40.8 / (5-1))==> 10.2
print(np.cov(D.iloc[:-1,0], D.iloc[:-1,1])[0,1]) #공분산
3. 상관관계(Correlation)
3-1) 공분산 (s_xy) > 0
==>대부분의 자료점이 제 1 , 제 3 사분면에 위치한다.
==> x가 증가하면 y도 증가하는 특성
==> x와 y는 양의 상관관계(Positive Correlation) 있다.
3-2) 공분산 (s_xy) < 0
==> 대부분의 자료점이 제 2, 제 4사분면에 위치
==> x가 증가하면 y는 감소하는 특성
==> x와 y는 음의 상관관계(Negative Correlation)
3-3) 공분산 (s_xy) = 0
==> 대부분의 자료점이 모든 사분면에 고르게 위치
==> x와 y 사이에 선형적 관계가 성립하지 않는다.
==> 무상관관계(None Correlation)
ax = sns.lmplot(x='최저' , y= '최고' , data = A )
4. 상관계수(Correlation Coefficient)
4-1 모상관계수(Population Correlation Coefficient)
==> 두 모집단 x와 y에 대한 모표준편차를 omega_x , omega_y , 모공분산을 omega_xy
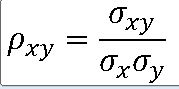
4-2 표본상관계수(Sample Correlation Coefficient)
==> 두 모집단 x와 y에 대한 표본표준편차를 s_x , s_y , 표본공분산을 s_xy
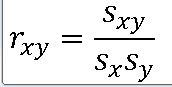
상관계수 r_xy 의 특성
1>
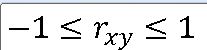
2>

==> x와 y는 양의 상관관계를 갖고, 양의 기울기를 갖는 적합선이 존재한다.
3>
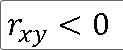
==> x와 y는 음의 상관관계를 갖고, 음의 기울기를 갖는 적합선이 존재한다.
4>
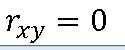
==> x와 y는 무상관관계를 갖는다.
5>
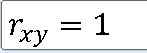
==> x와 y는 완전 양의 상관관계(Perfect Positive Correlation Coefficient)를 갖는다.
6>

==> x와 y는 완전 음의 상관관계(Perfect Negative Correlation Coefficient)를 갖는다.
EX)
A
gong_bun = np.cov(A['최저'] , A['최고'])[0,1] #표본공분산
# gong_bun = math.sqrt(gong_bun)
gong_bun1.9047619047619044
s_x = np.std(A['최저'] , ddof= 1)
s_y = np.std(A['최고'] , ddof =1)
print(s_x)
print(s_y)
corr = round(gong_bun / (s_x*s_y),4)
corr최저의 표본표준편차 : 1.1126972805283735
최고의 표본표준편차 : 1.7994708216848745
상관계수 : 0.9513
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 평균,표준편차,분산' 카테고리의 다른 글
| {0:02d}_Formating★.join(map(str , 변수)★사분위수★백분위수★기초통계학-[Chapter03 - 연습문제-02] (0) | 2022.12.09 |
|---|---|
| most_common()★.join(map(str , 변수)★np.argmax★np.bincount★최빈값★기초통계학-[Chapter03 - 연습문제] (0) | 2022.12.09 |
| annotate★IQR★boxplot★z-점수와 분위수★기초통계학-[Chapter03 - 09] (0) | 2022.12.07 |
| 변동계수★기초통계학-[Chapter03 - 08] (0) | 2022.12.07 |
| insert() , index★그룹화 자료의 분산과 표준편차★기초통계학-[Chapter03 - 07] (0) | 2022.12.07 |