전체 글
-
★산점도 그래프★이변량 양적자료★기초통계학-[Chapter02 - 03]2022.11.30
Plt, Fig, Seaborn 이해[Python]★기초통계학-[Chapter02 - 연습문제_02]
p46 2번문제
어느 대학에서 교내 음주의 찬성 여부를 재학생 100명 대상으로 조사
a = '찬성 찬성 찬성 무응답 찬성 무응답 찬성 반대 무응답 찬성 반대 무응답 찬성 반대 찬성 반대 찬성 찬성 무응답 찬성 찬성 반대 찬성 찬성 찬성 찬성 무응답 찬성 찬성 무응답 찬성 무응답 찬성 찬성 찬성 반대 반대 찬성 찬성 찬성 반대 반대 찬성 찬성 찬성 반대 반대 무응답 찬성 찬성 반대 찬성 반대 찬성 무응답 찬성 찬성 무응답 찬성 무응답 반대 찬성 찬성 반대 찬성 반대 찬성 반대 반대 찬성 찬성 반대 찬성 반대 찬성 찬성 반대 찬성 찬성 찬성 찬성 반대 반대 찬성 찬성 찬성 찬성 무응답 찬성 찬성 반대 찬성 찬성 찬성 반대 반대 찬성 반대 반대 무응답'
b = []
for i in a.split(' '):
b.append(i)
print(b)
print(len(b))['찬성', '찬성', '찬성', '무응답', '찬성', '무응답', '찬성', '반대', '무응답', '찬성', '반대', '무응답', '찬성', '반대', '찬성', '반대', '찬성', '찬성', '무응답', '찬성', '찬성', '반대', '찬성', '찬성', '찬성', '찬성', '무응답', '찬성', '찬성', '무응답', '찬성', '무응답', '찬성', '찬성', '찬성', '반대', '반대', '찬성', '찬성', '찬성', '반대', '반대', '찬성', '찬성', '찬성', '반대', '반대', '무응답', '찬성', '찬성', '반대', '찬성', '반대', '찬성', '무응답', '찬성', '찬성', '무응답', '찬성', '무응답', '반대', '찬성', '찬성', '반대', '찬성', '반대', '찬성', '반대', '반대', '찬성', '찬성', '반대', '찬성', '반대', '찬성', '찬성', '반대', '찬성', '찬성', '찬성', '찬성', '반대', '반대', '찬성', '찬성', '찬성', '찬성', '무응답', '찬성', '찬성', '반대', '찬성', '찬성', '찬성', '반대', '반대', '찬성', '반대', '반대', '무응답']
100
1. 도수표 작성
import collections
hashes = collections.Counter(b)
x = hashes.keys()
y = hashes.values()
c = pd.DataFrame({'응답' : x , '투표' : y})
c
ratio = []
for i in c['투표']:
ratio.append(round(i/sum(c['투표']),2)*100)
c['투표비율'] = pd.Series(ratio)
c
2. 도수막대그래프 작성
1. 도수막대그래프 두께 조절 및 갯수 위에 표시
fig = plt.figure(figsize = (8,8))
fig.set_facecolor('white')
ax = sns.barplot(x=c['응답'] , y=c['투표'])
ax.set_title('대학내 교내 음주의 찬성 여부' , fontsize= 18)
ax.set_xlabel('응답' , rotation = 0 , fontsize= 15 , labelpad=15)
ax.set_ylabel('투표', rotation = 0 , fontsize = 15 , labelpad=15)
ax.set_xticklabels(x, rotation = 0 , fontsize= 15)
width = 0.5
# 막대기의 두께 in Seaborn
for bar in ax.patches:
x = bar.get_x() # 막대 좌측 하단 x 좌표
old_width = bar.get_width() # 기존 막대 폭
bar.set_width(width) # 폭변경
bar.set_x(x+(old_width-width)/2) # 막대 좌측 하단 x 좌표 업데이트
for i,txt in enumerate(c['투표']):
b = txt
print(b)
if b == max(c['투표']):
ax.text(i, b+0.4, str(txt)+'개' , ha='center' , color = 'red' , fontweight = 'bold' , fontsize=17)
#어디 막대, 막대기의 위쪽에
else:
ax.text(i, b+0.5, str(txt)+'개' , ha='center' , color = 'dimgray' , fontsize=13 , fontweight = 'bold')

2. 도수 선그래프
fig = plt.figure(figsize = (8,8))
fig.set_facecolor('white')
ax2 = sns.lineplot(x=c['응답'] , y=c['투표'] , color='g', # 색상
linestyle='-', # 라인 스타일
marker='o') # 마커)
ax2.set_title('대학내 교내 음주의 찬성 여부' , fontsize= 18)
ax2.set_xlabel('응답' , rotation = 0 , fontsize= 15 , labelpad=15)
ax2.set_ylabel('투표', rotation = 0 , fontsize = 15 , labelpad=15)
ax2.set_xticklabels(x, rotation = 0 , fontsize= 15)
ax2.set_ylim(0, 70) #y축의 범위 지정
plt.show()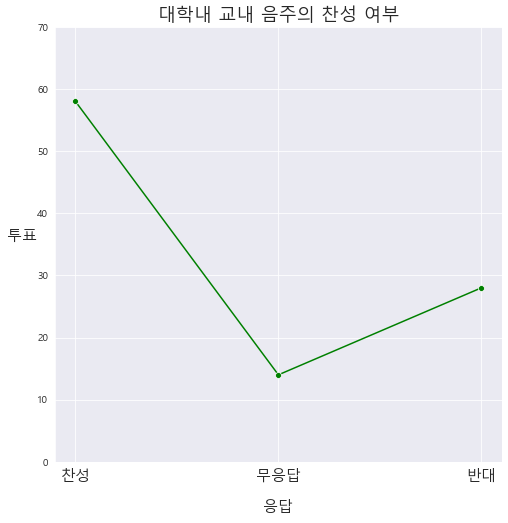
3. 상대도수 막대그래프
fig = plt.figure(figsize = (8,8))
fig.set_facecolor('white')
ax = sns.barplot(x=c['응답'] , y=c['투표비율'])
ax.set_title('대학내 교내 음주의 찬성 여부' , fontsize= 18)
ax.set_xlabel('응답' , rotation = 0 , fontsize= 15 , labelpad=15)
ax.set_ylabel('투표비율', rotation = 0 , fontsize = 15 , labelpad=15)
ax.set_xticklabels(c['응답'], rotation = 0 , fontsize= 15)
width = 0.5
# 막대기의 두께 in Seaborn
for bar in ax.patches:
x = bar.get_x() # 막대 좌측 하단 x 좌표
old_width = bar.get_width() # 기존 막대 폭
bar.set_width(width) # 폭변경
bar.set_x(x+(old_width-width)/2) # 막대 좌측 하단 x 좌표 업데이트
for i,txt in enumerate(round(c['투표비율'],2)): #근데 왜 round 해야하는지는 모르겠다.
b = txt
print(b)
if b == max(round(c['투표비율'],2)):
print('왜')
ax.text(i, b+0.4, str(txt)+'%' , ha='center' , color = 'red' , fontweight = 'bold' , fontsize=17)
#어디 막대, 막대기의 위쪽에
else:
ax.text(i, b+0.5, str(txt)+'%' , ha='center' , color = 'dimgray' , fontsize=13 , fontweight = 'bold')
4. 상대도수 선 그래프
fig = plt.figure(figsize = (8,8))
fig.set_facecolor('white')
ax2 = sns.lineplot(x=c['응답'] , y=c['투표비율'], color='g', # 색상
linestyle='-', # 라인 스타일
marker='o') # 마커)
ax2.set_title('대학내 교내 음주의 찬성 여부' , fontsize= 18)
ax2.set_xlabel('응답' , rotation = 0 , fontsize= 15 , labelpad=15)
ax2.set_ylabel('투표비율', rotation = 0 , fontsize = 15 , labelpad=15)
ax2.set_xticklabels(c['응답'], rotation = 0 , fontsize= 15)
ax2.set_ylim(0, 70) #y축의 범위 지정
plt.show()
5. 원그래프 (Pie Chart)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
colors = sns.color_palette('bright')[0:5]
plt.pie(c.loc[:,'투표비율'] , labels=c.loc[:,'응답'], labeldistance=1.2, autopct='%.1f%%' ,textprops={'fontsize' : 15})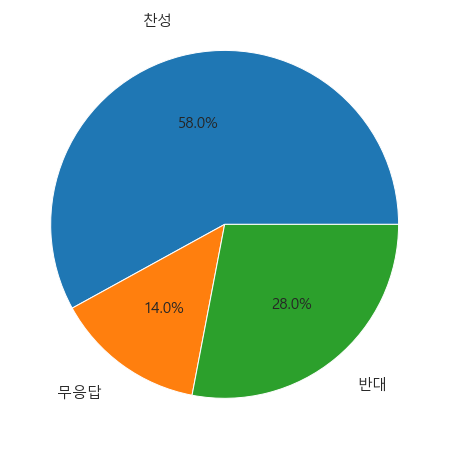
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 막대그래프,히스토그램' 카테고리의 다른 글
| ★axhline★막대그래프 기준선[Python]★기초통계학-[Chapter02 - 연습문제_04] (0) | 2022.12.01 |
|---|---|
| ★Pie Chart[Python]★기초통계학-[Chapter02 - 연습문제_03] (0) | 2022.12.01 |
| ★zip, collections.Counter()★도수표, 도수막대그래프★Plt, Fig, Seaborn 이해[Python]★기초통계학-[Chapter02 - 연습문제] (0) | 2022.11.30 |
| ★산점도 그래프★이변량 양적자료★기초통계학-[Chapter02 - 03] (0) | 2022.11.30 |
| ★양적자료의 요약★점도표, 도수분포표 , 특이점,계급 , 계급의 수★도수히스토그램★기초통계학-[Chapter02 - 02] (0) | 2022.11.29 |
★zip, collections.Counter()★도수표, 도수막대그래프★Plt, Fig, Seaborn 이해[Python]★기초통계학-[Chapter02 - 연습문제]
P46
고객 50명 대상으로 만족도 조사
GASAAIPIIGASSGPASSISPIPPPGASPIGIAGGSPASGPIAAGSSGGS==> 50명의 고객
1. 도수표 그리기
c = 'GASAAIPIIGASSGPASSISPIPPPGASPIGIAGGSPASGPIAAGSSGGS'
d = []
for i in c:
d.append(i)
dd = ['G', 'A','S', ·······················]
1. 리스트 데이터 프레임화 (zip , collections.Counter() 활용!)
import collections
hashes = collections.Counter(d) #hash로 처리하여 갯수 셀때 유용해진다.
x = list(hashes.keys())
y = list(hashes.values())
print(x)
print(y)
print(list(zip(x,y))) #zip은 각 index 별로 묶어준다.
c = pd.DataFrame(zip(x,y) , columns = ['범주' , '도수'])
cx = ['G', 'A', 'S', 'I', 'P']
y = [11, 10, 12, 8, 9]
list(zip(x,y)) = [('G', 11), ('A', 10), ('S', 12), ('I', 8), ('P', 9)]
==>zip은 index 별로 묶어준다.
2. 도수표의 상대도수 구하기
ratio = [round(i/sum(y) ,3)*100 for i in y]
c['상대도수'] = pd.Series(ratio)
c['상대도수'] = c['상대도수'].astype(str) +'%'
c==> 뒤에 '%' 붙일때 STR으로 형 변환 시키고 해야한다!

2. 도수막대그래프 그리기
※Seaborn은 Matplotlib을 기반으로 다양한 색상 테마와 통계용 차트 등의 기능을 추가한 시각화 패키지이다. 기본적인 시각화 기능은 Matplotlib 패키지에 의존하며 통계 기능은 Statsmodels 패키지에 의존
import platform
import matplotlib
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import font_manager, rc
import seaborn as sns
%precision 3
from matplotlib import pyplot as plt
%matplotlib inline
#그래프를 주피터 놋북에 그리기 위해
import numpy as np
import copy
from scipy.stats import probplot
from scipy import stats
#히스토그램 그리기
# Window
if platform.system() == 'Windows':
matplotlib.rc('font', family='Malgun Gothic')
elif platform.system() == 'Darwin': # Mac
matplotlib.rc('font', family='AppleGothic')
else: #linux
matplotlib.rc('font', family='NanumGothic')
# 그래프에 마이너스 표시가 되도록 변경
matplotlib.rcParams['axes.unicode_minus'] = False
# 한글 폰트 설정
font_location = 'C:/Windows/Fonts/MALGUNSL.TTF' #맑은고딕
font_name = font_manager.FontProperties(fname=font_location).get_name()
rc('font',family=font_name)1. Matplotlib 활용(bar() )
fig = plt.figure(figsize=(8,8)) #fig는 도화지
fig.set_facecolor('white') #fig의 배경색
plt.bar(x,y)
plt.title('고객별 만족도 조사')
plt.xlabel('범주' , rotation = 0 , fontsize = 15)
plt.ylabel('도수' , rotation = 0, fontsize = 15)
plt.xticks(rotation=0, fontsize=15) #xticks는 고객 명
2. Seaborn 활용(barplot() )
fig = plt.figure(figsize=(8,8)) #fig는 도화지
fig.set_facecolor('white') #fig의 배경색
ax = sns.barplot(x=c['범주'], y= c['도수'])
ax.set_title('고객별 만족도 조사')
ax.set_xlabel('범주' , rotation = 0 , fontsize = 15)
ax.set_ylabel('도수' , rotation = 0, fontsize = 15)
ax.set_xticklabels(x,rotation=0, fontsize=15) #xticks는 고객 명
3. 선그래프 그리기
1. Matplotlib 활용(Plot() )
fig = plt.figure(figsize=(8,8)) #plt는 matplotlib의 약자
fig.set_facecolor('white')
plt.plot(x,y)
plt.title('고객별 만족도 조사')
plt.xlabel('범주' , rotation = 0 , fontsize = 20)
plt.ylabel('도수' , rotation = 0, fontsize = 20)
plt.xticks(rotation=0, fontsize=20) #xticks는 고객 명
2. Seaborn 활용(lineplot() )
fig = plt.figure(figsize=(8,8)) #plt는 matplotlib의 약자
fig.set_facecolor('white')
ax = sns.lineplot(x=x, y=y,
color='r', # 색상
linestyle='-', # 라인 스타일
marker='o') # 마커
#ax 변수에 저장
ax.set_title('고객별 만족도 조사')
ax.set_xlabel('범주', fontsize = 15 , fontweight = 'bold')
ax.set_ylabel('업무량' , fontsize = 15 , fontweight = 'bold' , rotation = 0 , labelpad=25)
ax.set_xticklabels(x, fontsize=15) #set_xticklabels(축별 이름 , font 크기)| Matplotlib | Seaborn |
| plt.title | sns.set_title |
| plt.xlabel() | sns.set_xlabel() |
| plt.xticks | sns.set_xticklabels() |

4. 상대도수막대그래프 그리기(위에 값 붙이기)
fig = plt.figure(figsize=(8,8)) #fig는 도화지
fig.set_facecolor('white') #fig의 배경색
ax = sns.barplot(x=c['범주'], y= c['상대도수'])
ax.set_title('고객별 만족도 조사')
ax.set_xlabel('범주' , rotation = 0 , fontsize = 15)
ax.set_ylabel('상대도수' , rotation = 0, fontsize = 15 , labelpad= 20)
ax.set_xticklabels(x,rotation=0, fontsize=15) #xticks는 고객 명
for i,txt in enumerate(c['상대도수']):
b = int(txt)
if b == max(c['상대도수']):
ax.text(i, b+0.4, str(txt)+'%' , ha='center' , color = 'red' , fontweight = 'bold' , fontsize=17)
#어디 막대, 막대기의 위쪽에
else:
ax.text(i, b+0.5, str(txt)+'%' , ha='center' , color = 'dimgray' , fontsize=13 , fontweight = 'bold')
5. 상대도수 선그래프 그리기
fig = plt.figure(figsize=(8,8)) #plt는 matplotlib의 약자
fig.set_facecolor('white')
ax = sns.lineplot(x=x, y=c['상대도수'],
color='r', # 색상
linestyle='-', # 라인 스타일
marker='o') # 마커
#ax 변수에 저장
ax.set_title('고객별 만족도 조사')
ax.set_xlabel('범주', fontsize = 15 , fontweight = 'bold')
ax.set_ylabel('상대도수' , fontsize = 15 , fontweight = 'bold' , rotation = 0 , labelpad=25)
ax.set_xticklabels(x, fontsize=15) #set_xticklabels(축별 이름 , font 크기)
6. 원 그래프(Pie 그래프 그리기)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
colors = sns.color_palette('bright')[0:5]
plt.pie(c.loc[:,'도수'] , labels=c.loc[:,'범주'], labeldistance=1.2, autopct='%.1f%%' ,textprops={'fontsize' : 15})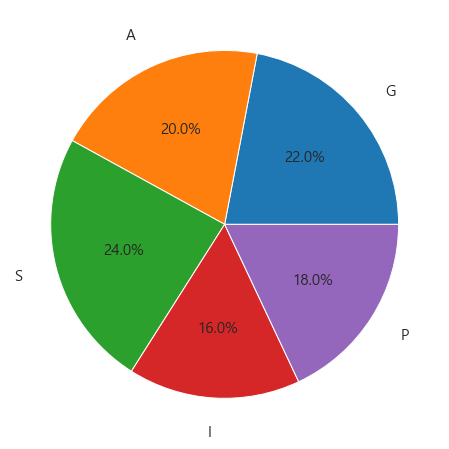
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 막대그래프,히스토그램' 카테고리의 다른 글
| ★Pie Chart[Python]★기초통계학-[Chapter02 - 연습문제_03] (0) | 2022.12.01 |
|---|---|
| Plt, Fig, Seaborn 이해[Python]★기초통계학-[Chapter02 - 연습문제_02] (0) | 2022.11.30 |
| ★산점도 그래프★이변량 양적자료★기초통계학-[Chapter02 - 03] (0) | 2022.11.30 |
| ★양적자료의 요약★점도표, 도수분포표 , 특이점,계급 , 계급의 수★도수히스토그램★기초통계학-[Chapter02 - 02] (0) | 2022.11.29 |
| ★질적자료의 요약★seaborn, matplotlib★기초통계학-[Chapter02 - 01] (0) | 2022.11.29 |
★산점도 그래프★이변량 양적자료★기초통계학-[Chapter02 - 03]
EX) 경쟁관계에 있는 두 고등학교 학생들의 학업 능력, 여성 근로자와 남성 근로자의 생산량과 같이 서로 비교되는 두 자료 집단의 관찰값 비교
==> 점도표 , 도수다각형 또는 줄기-잎 그림을 사용하면 편리하다.
산점도
두 종류의 자료가 독립변수, 응답변수의 관계
수평축에 독립변수 x를 , 수직축에 응답변수 y를 기입하여 순서쌍 (x,y)를 점으로 나타낸 그림이다.
a = pd.DataFrame({'팀' : ['뉴욕' , '토론토' , '볼티모어' , '보스턴' , '템파베이' , '클리브랜드' , '디트로이트' ,
'시카고' , '켄자스시티' , '미네소타' , '애너하임' , '텍사스' , '시애틀' , '오클랜드'],
'승리한 경기수' : [103,78,67,93,55,74,55,81,62,94,99,72,93,103],
'평균타율' : [0.275,0.261,0.246,0.277,0.253,0.249,0.248,0.268,0.256,0.272,0.282,0.269,0.275,0.261]})
a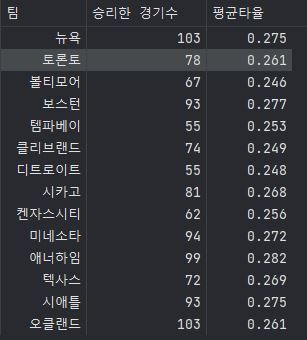
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.scatter(a['승리한 경기수'], a['평균타율'])
plt.xlabel('승리한 경기 수(개)')
plt.ylabel('평균 타율')
plt.show()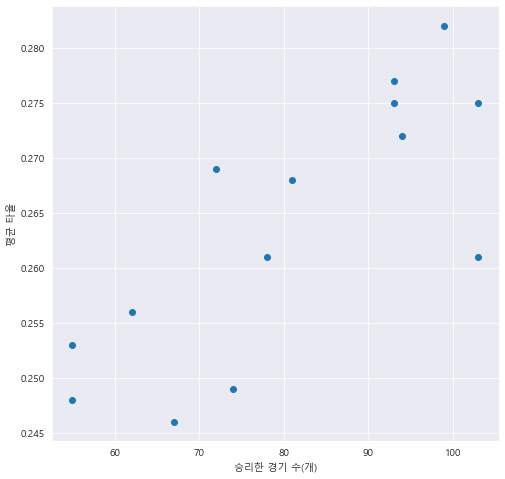
==> 산점도로부터, 승리한 경기 수가 많을 수록 평균 타율이 높고,
승리한 경기 수가 적을수록 타율이 낮다는 결론을 얻을 수 있다.
b = pd.DataFrame({'전용면적(m**2)' : [93.75,84.88,44.33,59.82,116.46,41.30,45.90,41.30,41.30,49.94,58.01,58.01,41.30,41.30,45.77,41.30,41.30,58.01,60.50,59.20,31.98,59.28,41.30,45.77,49.94,31.95,38.52,45.90] ,
'실거래가 가격(만원)' : [40800,44000,16600,28800,35300,17500,16900,14000,16900,18600,21400,22500,15750,14000,14750,17300,17700,25300,21800,23100,17150,27000,20000,18900,22800,16000,23000,16000]})
b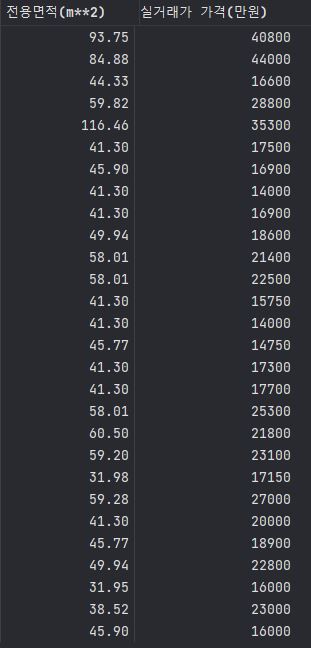
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.scatter(b['전용면적(m**2)'], b['실거래가 가격(만원)'])
plt.xlabel('전용면적(m**2)')
plt.ylabel('실거래가 가격(만원)')
plt.show()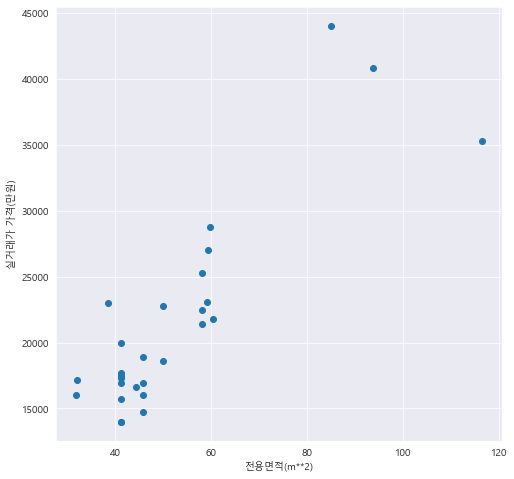
==> 산점도로부터, 전용면적이 작을수록 실거래가 가격이 낮음을 알 수 있다.
==> 산점도의 경우 독립변수(x) 와 응답변수(y)의 값이 모두 양적변수여야 한다.
https://knowallworld.tistory.com/189
==> 재외공관 코드와 단수_복수_합계로 그래프를 그릴 수 없다.
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 막대그래프,히스토그램' 카테고리의 다른 글
| ★Pie Chart[Python]★기초통계학-[Chapter02 - 연습문제_03] (0) | 2022.12.01 |
|---|---|
| Plt, Fig, Seaborn 이해[Python]★기초통계학-[Chapter02 - 연습문제_02] (0) | 2022.11.30 |
| ★zip, collections.Counter()★도수표, 도수막대그래프★Plt, Fig, Seaborn 이해[Python]★기초통계학-[Chapter02 - 연습문제] (0) | 2022.11.30 |
| ★양적자료의 요약★점도표, 도수분포표 , 특이점,계급 , 계급의 수★도수히스토그램★기초통계학-[Chapter02 - 02] (0) | 2022.11.29 |
| ★질적자료의 요약★seaborn, matplotlib★기초통계학-[Chapter02 - 01] (0) | 2022.11.29 |
★Sympy 이용 PYTHON 미분★딥러닝 기초수학★Tensorflow이용 머신러닝-02 딥러닝★
함수 : 두 집합 사이의 관계를 설명하는 수학 개념
==> 변수 x와 y가 있을때 x가 변하면 y는 어떤 규칙으로 변하는지를 나타낸다.
y = f(x) 로 표시한다.
일차함수 :
==> y가 x에 대한 일차식으로 표현
y = ax + b( a != 0)
a는 기울기 , b는 y 절편이라 한다.
이차함수 :
==> y가 x에 대한 이차식으로 표현
y = ax^2( a!=0)
import matplotlib.pyplot as plt
import numpy as np#x값 설정
x = np.array(range(-10, 11))
print('x : ' , x)
#축 이름 설정
plt.xlabel('x axis')
plt.ylabel('y axis')
#그리드 추가
plt.grid(color = 'gray' , alpha = .5 , linestyle = '--')
#방정식 추가하기
plt.plot(x, x**2-15 , label= 'y = x**2 -15')
#범례 작성
plt.legend()
plt.show()
==> 포물선의 맨 아래에 위치한 지점이 최솟값 ==> 딥러닝을 실행할 때 이 최솟값을 찾아내는 과정이 매우 중요
미분, 순간 변화율과 기울기 :
미분 : y = ax**2 에서 x값이 a일때 그래프의 기울기 ==> y' = 2ax ==> 2a**2
순간변화율 : 어느 쪽을 향하는 방향성을 지닌다.
==> 방향을 따라 직선을 길게 그려주면 그래프와 맞닿은 접선이 그려진다.
==> 이 선이 점에서의 기울기가 된다.
==> 미분을 한다는 것은 쉽게 말해 이 '순간 변화율'을 구한다는 것이다.
==> 어느 순간에 변화가 일어나고 있는지를 숫자로 나타낸 것을 미분계수라고 한다. ==> 미분계수는 곧 그래프에서의 기울기 의미한다.
==> 기울기가 0일때 즉 미분계수의 값이 0이 될때가 최솟값이 된다.
================================
PYTHON 미분
#!pip install --trusted-host pypi.python.org --trusted-host files.pythonhosted.org --trusted-host pypi.org sympySympy 모듈 설치
from sympy import Derivative, symbols
x = symbols('x') #x를 기호변수화
function_s = x**4 + 6*x**3 + x + 1
fprime = Derivative(function_s, x).doit() #x에 대해서 미분
#.doit() 무조건 해주어야한다.
print("function_s 의 도함수 : {}".format(fprime))
fdoubleprime = Derivative(fprime, x).doit() # fprime 에 대하여 미분
print("function_s의 이계도함수 : {}".format(fdoubleprime))
==> 도함수는 F(X)의 미분한 방정식 의미
==> 이계도함수는 F''(X)를 의미
'딥러닝 > 선형회귀_로지스틱회귀' 카테고리의 다른 글
| ★vlines()★선형회귀★평균제곱 오차(MSE)★Tensorflow이용 머신러닝-[Chapter 03-01]딥러닝★ (0) | 2022.12.08 |
|---|---|
| ★Tensorflow이용 머신러닝-01 딥러닝★ (0) | 2022.11.28 |
GIT HUB 와 DATA SPELL 연동하기(COMMIT & PULL & UPDATE)
1. 상단 메뉴바 Git ==> Clone

2. URL ==> 레파리토지 주소
Directory ==> 로컬 드라이브 폴더 주소

3. Trust Project

4. Git ==> Commit 클릭

5. Commit Message 입력 ==> Commit and Push

6. Push 클릭

7. GIT 업로드 완료

8. GIT PULL 하기 (BUT. CLONE 중이라 PULL 할 필요 없다.)

9. Update Project 클릭 ==> Git에 파일 업로드시 IDE에 똑같이 반영 시킬 수 있다.

'IT에대해 알아보자 > 깃허브사용법' 카테고리의 다른 글
| GIT HUB LFS(100mb넘는 대용량 파일 커밋) 사용하기 (0) | 2022.09.16 |
|---|---|
| [GITHUB] Branch 활용하기 (0) | 2022.09.10 |
| 왕초보도 따라할수 있는 GITHUB 설치 및 로그인[GITHUB 다뤄보기-1] (0) | 2021.07.09 |
| 왕초보도 따라할수 있는 GITHUB 레파라토지(Repositories) 생성[GITHUB 다뤄보기-2] (0) | 2021.06.28 |
| 왕초보도 따라할수 있는 깃허브 레파라토지(Repositories)에 업로드하는법 [Git Bash, Git HUB 다뤄보기 -3] (0) | 2021.06.28 |
[외교부 인턴 일지- d+85 2022.11.29]데이터 분석 청년인재 양성 사업
1. 실생활 통계(2.1~2.4)
==> 2.3까지
2. 프로그래머스 스택,큐 2문제
3. 딥러닝 (선형회귀_3 진행)
==> 2까지 ==> sympy 정리
4. 분석 과정 정리
==> 못함
내일 할일
1. 월간 보고서 작성
2. 출석부 작성
3. 실생활 통계(2.3~2.4)
4. 딥러닝 (선형회귀_3 진행)
==> sympy 정리
5. 분석과정 정리
'인턴일지 > 외교부_일지' 카테고리의 다른 글
| [외교부 인턴 일지- d+115 2022.12.26]데이터 분석 청년인재 양성 사업 (0) | 2022.12.29 |
|---|---|
| [외교부 인턴 일지- d+109 2022.12.23]데이터 분석 청년인재 양성 사업 (1) | 2022.12.23 |
| [외교부 인턴 일지- d+100 2022.12.14]데이터 분석 청년인재 양성 사업 (0) | 2022.12.14 |
| [외교부 인턴 일지- d+86 2022.11.30]데이터 분석 청년인재 양성 사업 (0) | 2022.12.01 |
| [외교부 인턴 일지- d+84]데이터 분석 청년인재 양성 사업 (0) | 2022.11.28 |
★양적자료의 요약★점도표, 도수분포표 , 특이점,계급 , 계급의 수★도수히스토그램★기초통계학-[Chapter02 - 02]
점도표 :
각 범주 또는 측정값을 수평축에 나타내고,
이 수평축 위에 각 범주 또는 측정값의 관찰 횟수를 점으로 나타낸 것이다.
==> 원자료의 특성을 그림으로 나타내는 가장 간단한 방법
==> 양적자료뿐만 아니라 질적자료에도 사용이 가능하다.

점도표는 수평축 위에 범주 또는 측정값을 점으로 찍어서 나타냄
==> 자료의 정확한 위치를 알 수 있으며, 수집한 자료가 어떠한 모양으로 흩어져 있는지 쉽게 파악 가능
=============
도수분포표(Frequency distribution table) : 양적자료를 적당한 간격으로 집단화(범주화) 하면 질적 자료로 전환시킬 수 있다.
==> 각 계급 또는 구간 안에 들어가는 자료의 도수, 상대도수, 누적도수, 누적상대도수, 계급값
계급(CLASS) : 양적자료를 적당한 간격으로 집단화 ==> 범주 의미
계급 간격(CLASS Width) : 이웃하는 두 계급의 위쪽 경계에서 아래쪽 경계를 뺀 값
계급 상대도수(Class Relative Frequency) : 계급의 도수를 자료 집단 안의 전체 자료의 수로 나눈 값
계급 상대도수 = 계급의 도수 / 전체 도수
누적 도수(Cumulative Frequency) : 이전 계급까지의 모든 도수를 합한 도수
누적상대도수(Cumulative relative frequency) : 이전 계급까지의 모든 상대도수를 합한 상대도수
계급값(Class Mark) : 각 계급의 중앙값
계급값 = (위쪽 경계 + 아래쪽 경계) / 전체 도수
================================
양적자료의 도수분포표의 작성 프로세스
1번째 , 계급의 수를 결정한다.
보통 계급의 수 : 5개~20개 내외
자료의 수 (n)이 200개 이하이면 계급의 수(k)는 k= n^(1/2) +- 3 에 가까운 정수 선택
자료의 수가 충분히 많으면
Sturges 공식 활용 ==> k= 1+3.3log n 에 가까운 정수를 택한다.
EX) 재외공관의 개수 193개 ==> k = 193^(1/2)+-3 = 16~17 개의 계급의 수를 정한다.

2번째 , 각 계급에 일정하게 주어지는 각 계급 간격을 결정한다.
범위(Range)
==> R는 R=(최대 자료 값) - (최소 자료 값)
계급 간격(Class Width) ==> 범위를 계급의 수(k)로 나눈 값보다 큰, 가장 작은 정수로 택한다.
계급간격(w) ~~ R/k
R = 86995 - 25283 = 61,712
k = 16
w= 3857
3번째, 이웃하는 계급 사이의 중복을 피하기 위하여 제 1계급의 하한을 결정
제 1계급의 하한 = 최소 자료 값 - (기본단위)/2
==> 제 1계급의 하한 = 25283- 1/2 = 25,283.5
4번째 , 각 계급의 도수, 상대도수, 누적도수, 누적상대도수, 계급값을 구하여 기입하면 도수분포표가 완성
================================
도수히스토그램
==> 수평축에 도수분포표의 계급을 나타내고 , 수직축에 각 계급에 대응하는 도수를 높이로 갖는 사각형으로 나타낸 그림

plt.hist(dansu_boksu_hab.iloc[:,-1] , bins , rwidth = 0.8 , color = 'green' , alpha = 0.5)
plt.xlabel('재외공관 별 업무량' , fontsize = 14)
plt.xticks(fontsize = 14)
plt.yticks(fontsize = 14)

특이점 (Outlier) : 분포 모양에서 멀리 떨어지는 자료의 측정값
data = [12.6,10.5,25.2,20.9,29.5,28.3,12.9,11.2,26.1,23.6,18.2,13.1,14.8,11.1 , 10.2,
16.9,26.7,16.7 , 23.6 , 17.5]
width = (max(data) - min(data)) // 5 #계급 간격 구하는 공식bins = np.arange(min(data), max(data), width)
hist, bins = np.histogram(data, bins)
print(hist)
print(bins)HIST : [7 1 4 1 2 3]
BINS : [10.2 13.2 16.2 19.2 22.2 25.2 28.2]
plt.hist(data, bins , rwidth = 0.8 , color = 'green' , alpha = 0.5)
plt.xlabel('양적자료' , fontsize = 14)
plt.xticks(fontsize = 14)
plt.yticks(fontsize = 14)
================================
도수다각형
==> 히스토그램에서 각 사각형 상단의 중심을 선분으로 연결하여 다각형으로 나타낸 그림
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 막대그래프,히스토그램' 카테고리의 다른 글
| ★Pie Chart[Python]★기초통계학-[Chapter02 - 연습문제_03] (0) | 2022.12.01 |
|---|---|
| Plt, Fig, Seaborn 이해[Python]★기초통계학-[Chapter02 - 연습문제_02] (0) | 2022.11.30 |
| ★zip, collections.Counter()★도수표, 도수막대그래프★Plt, Fig, Seaborn 이해[Python]★기초통계학-[Chapter02 - 연습문제] (0) | 2022.11.30 |
| ★산점도 그래프★이변량 양적자료★기초통계학-[Chapter02 - 03] (0) | 2022.11.30 |
| ★질적자료의 요약★seaborn, matplotlib★기초통계학-[Chapter02 - 01] (0) | 2022.11.29 |
★질적자료의 요약★seaborn, matplotlib★기초통계학-[Chapter02 - 01]
질적자료 :
수집한 자료가 어떤 의미를 제공하는지 알기 쉽게 정리하고 요약할 필요가 있다.
==> 표와 그래프를 이용하여 수집한 자료를 정리하고 요약한다면 시각적으로 자료의 특성을 쉽게 알 수 있다.
도수(Frequency) : 각 범주 안에 들어가는 자료 집단에서 관찰된 자료의 수를 의미
상대도수(Relative Frequency) : 각 범주의 도수를 전체 도수로 나눈 값
상대도수 = 범주의 도수 / 전체 도수
EX) 어느 학교 40명의 혈액형을 조사한 결과 A형이 11명, B형이 9명, AB형이 6명, O형이 14명
각 범주에 해당하는 상대도수 :
A형 : 11/40 = 0.275
B형: 9/40 = 0.225
AB형 : 6/40 =0.15
O형: 14/40 =0.35
============================
막대 그래프
==> 각 범주에 대응하는 도수 또는 상대 도수, 백분율 등을 같은 폭의 수직 막대로 나타낸 그림을
막대그래프(bar chart)라고 한다.
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import font_manager, rc
import seaborn as snsax2 = plt.subplots() #그래프 바탕 생성
ax2 = sns.barplot(x = '재외공관' , y='단수_복수_합계',data=dansu_boksu_11)
ax2.set_title('재외공관별 업무량' , fontsize = 10)
ax2.set_xlabel('재외공관')
ax2.set_ylabel('업무량' )
ax2.tick_params(axis='x', rotation=45) #x축 rotation 돌리기
#ax2.xticks()
#ax.xticks(rotation=75)
plt.rc('axes', labelsize=8) # x,y축 label 폰트 크기
plt.rc('xtick' ,labelsize=8) # x축 눈금 폰트 크기
plt.rc('ytick', labelsize=8) # y축 눈금 폰트 크기
plt.show()
위와 같이 범주의 도수 또는 백분율이 점점 감소하도록 범주를 재배열한 그래프를
파레토 그래프(Pareto chart)라 한다.
============================
원그래프 : 원을 자료의 범주 개수만큼 파이 모양의 여러 조각으로 나누어 작성한 그림을 원그래프(Pie chart)
==> 각 범주를 상대적으로 비교할 때 많이 사용한다.
plt.pie(dansu_boksu_10.loc[:,'단수_복수_합계'] ,
labels=dansu_boksu_10.loc[:,'재외공관'], labeldistance=1.2, autopct='%.1f%%')

===============================
[I Can do]자료의 각 후보별 득표수와 득표비율
import matplotlib.pyplot as plt
# 데이터 정의
categories = ['A', 'B', 'C', 'D'] # 변수 이름
values = [2096294, 2726763, 23325, 17401] # 득표 수
total_votes = sum(values) # 총 득표수
percentages = [v / total_votes * 100 for v in values] # 득표 비율 계산
# 그래프 크기 설정
plt.figure(figsize=(12, 6))
# 첫 번째 그래프: 득표 수
plt.subplot(1, 2, 1) # 1행 2열 중 첫 번째 그래프
plt.bar(categories, values, color='skyblue', edgecolor='black', width=0.6)
plt.title('Votes')
plt.xlabel('Categories')
plt.ylabel('Votes')
for i, v in enumerate(values):
plt.text(i, v + total_votes * 0.01, str(v), ha='center', fontsize=10)
# 두 번째 그래프: 득표 비율
plt.subplot(1, 2, 2) # 1행 2열 중 두 번째 그래프
plt.bar(categories, percentages, color='orange', edgecolor='black', width=0.6)
plt.title('Vote Percentages')
plt.xlabel('Categories')
plt.ylabel('Percentages (%)')
for i, p in enumerate(percentages):
plt.text(i, p + 0.5, f'{p:.2f}%', ha='center', fontsize=10)
# 그래프 간격 조정 및 출력
plt.tight_layout()
plt.show()

출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 막대그래프,히스토그램' 카테고리의 다른 글
| ★Pie Chart[Python]★기초통계학-[Chapter02 - 연습문제_03] (0) | 2022.12.01 |
|---|---|
| Plt, Fig, Seaborn 이해[Python]★기초통계학-[Chapter02 - 연습문제_02] (0) | 2022.11.30 |
| ★zip, collections.Counter()★도수표, 도수막대그래프★Plt, Fig, Seaborn 이해[Python]★기초통계학-[Chapter02 - 연습문제] (0) | 2022.11.30 |
| ★산점도 그래프★이변량 양적자료★기초통계학-[Chapter02 - 03] (0) | 2022.11.30 |
| ★양적자료의 요약★점도표, 도수분포표 , 특이점,계급 , 계급의 수★도수히스토그램★기초통계학-[Chapter02 - 02] (0) | 2022.11.29 |