★균등분포★scipy.stats.uniform.pdf(x= , loc= , scale=)★np.where()★평균_분산구할때_오차줄이기★기초통계학-[Chapter06 - 연습문제-10]

7. 1.5V 건전지는 1.45V에서 1.65V 사이에서 균등분포를 이룬다.

https://knowallworld.tistory.com/252

sympy INTEGRAL,Symbol,pprint★scipy.stats.UDF_균등분포★stats.PDF_확률밀도함수★기초통계학-[Chapter06 - 연속

1> 임의로 하나 선정 ==> 기대되는 전압(E(X) ) 과 표준편차(루트(V(X)))

 

 

X ~ U(1.45, 1.65)

 

균등분포의 평균

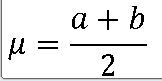
print( (1.45 + 1.65) / 2)

print(np.mean(np.arange(min,max, .01)))

==> x축의 간격들을 평균처리

==> 1.55

 

균등분포의 분산

print( math.pow(1.65 - 1.45,2) / 12)

print(np.var(np.arange(min,max, .01)))

==> x축의 간격들을 분산처리!!!

==> 0.0033

 

2>건전지 전압이 1.5V 보다 작을 확률

P(1.45<=X<=1.5) =  0.25

#1.5V 건전지는 1.45V에서 1.65V 사이에서 균등분포를 이룬다.

min , max = 1.45, 1.65

# x_2 = linspace(min-1 , max+1 , 100)

x_2 = np.arange(min-.2 , max+.2 , .01)

print(x_2)

y = scipy.stats.uniform.pdf( x = x_2 , loc = min , scale = max-min)

print(y)

print(len(y[np.where(y != 0.)])) #np.where 활용

==> np.where 조건절로 원하는 값 추출 가능(0. 아닌것들 추출)

 

[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 5. 5. 5. 5.
 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
20

 

fig = plt.figure(figsize=(12, 8))

ax = sns.lineplot(x = x_2 , y= y)

ax.set_title('균등분포(Uniform Distribution)')
ax.set_xlabel('X' , fontsize= 15)
ax.set_ylabel('Y' , fontsize= 15 , rotation = 0 , labelpad = 12)
a = scipy.stats.uniform.pdf( x = 1.5 , loc = 1.45 , scale = 1.65-1.45) #scipy.stats.uniform.pdf( x = 1.5 , loc = min , scale = max-min)
print(a)
ax.vlines(1.5 , ymin = 0 , ymax = a , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.fill_between(x_2 , a , 0 , where = (x_2<= 1.5001) & (x_2>= 1.445)) #오차있으므로 신경 끄자.

area = (1.5 - 1.45)*a #넓이 구하기!!!!!
print(area)
ax.text(1.51 , 3, 'P(1.45=<X<=1.5)' + f"= {round(area,4)}",fontsize=15)

==> scipy.stats.uniform.pdf( x = 어디까지 확률을 구할것인가, loc= 균등분포에서 제일 작은값 , scale = 균등분포 제일 끝값끼리의 차) 

균등분포 그래프

==> 중간에 빈칸들은 np.arange()값을 세분화 시키면 사라진다.

 

x_2 = np.arange(min-.2 , max+.2 , .001)
y = scipy.stats.uniform.pdf(x = x_2 , loc = 1.45 , scale = 1.65-1.45)
print(y)



fig = plt.figure(figsize=(12, 8))

ax = sns.lineplot(x = x_2 , y= y)

ax.set_title('균등분포(Uniform Distribution)')
ax.set_xlabel('X' , fontsize= 15)
ax.set_ylabel('Y' , fontsize= 15 , rotation = 0 , labelpad = 12)
a = scipy.stats.uniform.pdf( x = 1.5 , loc = 1.45 , scale = 1.65-1.45) #scipy.stats.uniform.pdf( x = 1.5 , loc = min , scale = max-min)
print(a)
ax.vlines(1.5 , ymin = 0 , ymax = a , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.fill_between(x_2 , a , 0 , where = (x_2<= 1.5) & (x_2>= 1.45)) #오차있으므로 신경 끄자.

area = (1.5 - 1.45)*a #넓이 구하기!!!!!
print(area)
ax.text(1.51 , 3, 'P(1.45=<X<=1.5)' + f"= {round(area,4)}",fontsize=15)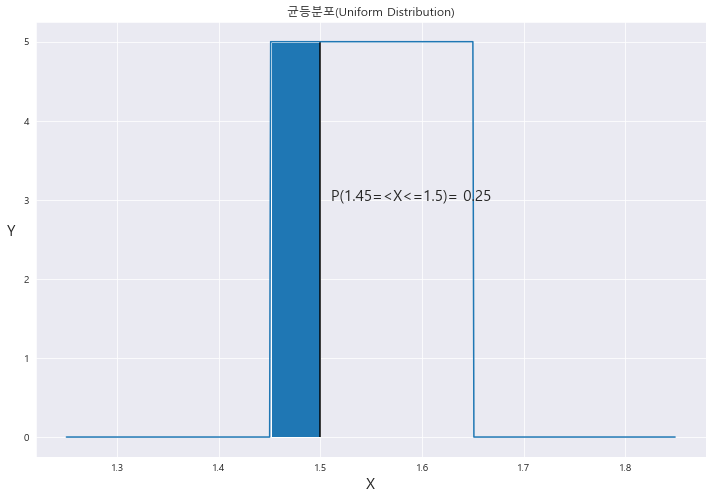

균등분포_오차 줄이기

3>10개의 건전지가 들어있는 상자 안에 1.5V보다 전압이 낮은 건전지의 수의 평균과 분산 ==> 베르누이 시행

 

https://knowallworld.tistory.com/241

이항분포식★이항실험★이항분포의 평균,분산★베르누이시행★기초통계학-[Chapter05 - 이산확률

 

1.5V 보다 작을 확률 = 0.25

 

X ~ B(10 , 0.25)

 

E(X) = 10* 0.25 = 2.5

V(X) = 2.5 * 0.75 = 1.875

 

 

4> 1.5V 보다 낮은 전압을 가진 건전지가 4개 이상 들어있을 확률 ==> 이항분포 , 이항정리 잘 기억!

 

https://knowallworld.tistory.com/256

[PYTHON]_코테에서도 쓰일_조합_계산_파스칼의 삼각형_시간복잡도(이항정리, 이항계수) 사용하기!!

P(Y>=4) = 1- P(Y<3) = 

 

f(x=3) = 10C4 * (0.25**3) * (0.75**7)

res = 0
for i in range(4):
    a = len(list(itertools.combinations(np.arange(10) , i)))
    print(a)
    b = math.pow(0.25 , i) * (math.pow(0.75 , 10-i))

    c = a*b
    print(c)
    res+=c
print(1- res)

0.22412490844726562

 

 

8. 버스는 오후 1시부터 5시까지 40분 간격, 버스 기다리는 시간은 0에서 40분까지 균등하게 분포를 이룬다.

 

1> 버스를 기다리는 시간에 대한 확률 밀도함수

 

f(x) = 0.025 (0<x<40)

  0 (otherwise)

 

2>기다리는 시간의 평균과 표준편차

means = np.mean(x[np.where((x>= 0) & (x<=40))])
#np.where 사용시 ndarray로 한번더 묶어줘야한다.
print(means)
vars = np.var(x[np.where((x>= 0) & (x<=40))])

==> np.where 사용시 ==> array의 변수로 리스트화 하여 묶어줘야한다!!!

 

E(X) =  20

V(X) = 133.3325

print("what?! {}".format(np.std(np.arange(0,40,.1))))
print("what?! {}".format(np.var(np.arange(0,40,.1))))

==> 1단위일때 1/10 단위로 np.arange()처리하면 오차를 줄일 수 있다!!!

표준편차 = 루트(140) = 11.547

 

 

3> 15분 이상 기다릴 확률

fig = plt.figure(figsize= (15,8))

ax = sns.lineplot(x= x , y= y)

ax.hlines(y= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , xmin = 0-2 , xmax  =45)

ax.vlines(x= 15 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')

ax.fill_between(x , y , 0 , where = (x<= 40) & (x>= 15)) #오차있으므로 신경 끄자.
ax.text(-8 , scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , "y = {}".format(round(scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min),7)), fontsize =  14)

#area = P(X>=15) = 1 - P(X<=15) ===> 균등분포는 연속확률분포다!!! 이산확률분포로 생각하면 안된다!!
area = 1 - (scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) *15)


ax.text(5 ,0.020 , "P(X>=15) = {}".format(round(area,3)), fontsize =  14)

==> 균등분포는 연속확률분포이다!!!! P(X>=15) = 1-P(X<15) 이다!!!

균등분포_3

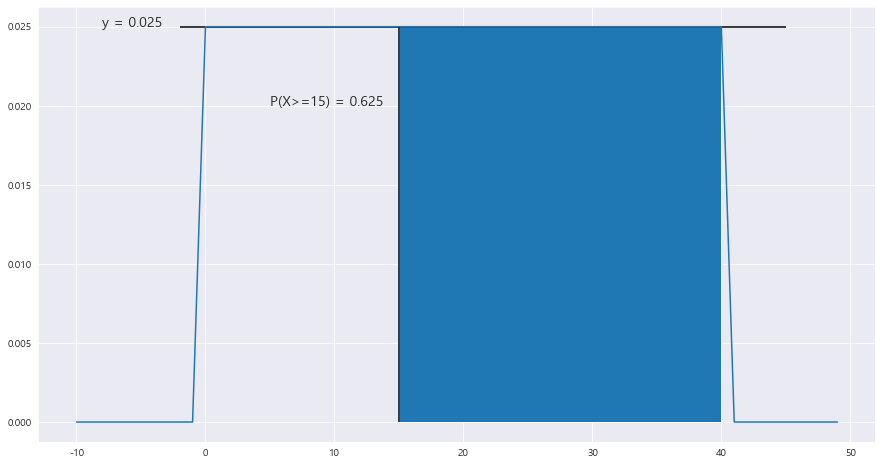
P(X>=15) = 0.625

 

4> 기다리는 시간이 5분에서 10분 사이일 확률

 

fig = plt.figure(figsize= (15,8))

ax = sns.lineplot(x= x , y= y)

ax.hlines(y= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , xmin = 0-2 , xmax  =45)

ax.vlines(x= 10 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')
ax.vlines(x= 5 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')

ax.fill_between(x , y , 0 , where = (x<= 10) & (x>= 5)) #오차있으므로 신경 끄자.
ax.text(-8 , scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , "y = {}".format(round(scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min),7)), fontsize =  14)

#area = P(5<=X<=10) = P(X<=10) - (X<=4)
area = (scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) *10) - (scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) *5)


ax.text(15 ,0.020 , "P(5<=X<=10) = {}".format(round(area,3)), fontsize =  14)

==> 균등분포는 연속확률분포이다!!!! P(5<=X<=10) = P(X<=10) - P(X<5) 이다!!!

균등분포_4

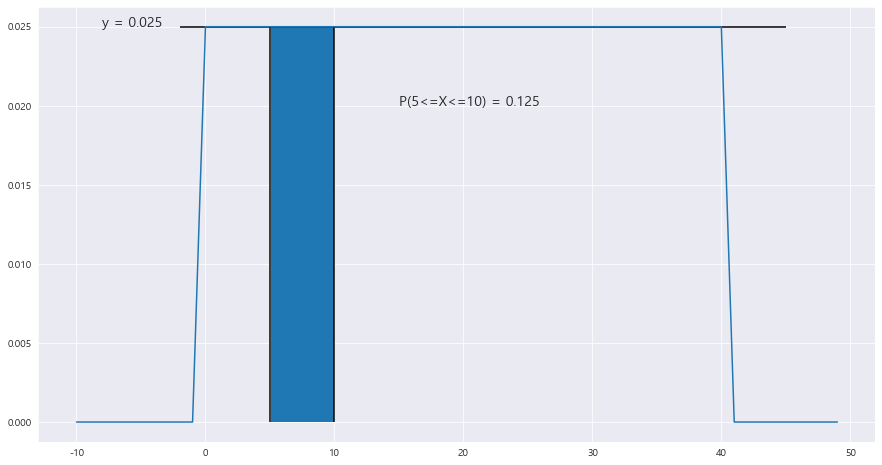
P(5<=X<=10) = P(X<=10) - P(X<=5) = 0.125

 

 

9. 연간 1인당 지출하는 보험료는 최소 25만원부터 최대 300만원 사이의 균등분포

 

1> 보험료로 지출하는 평균 금액과 표준편차를 구하라.

 

min , max = 25 , 300

x = np.arange(min - 25 , max + 25 , 1)

y = scipy.stats.uniform.pdf(x=x , loc= min , scale = max-min)

print(y)

print("평균 지출금액 : {}".format(np.mean( x[np.where( (x>=25) & (x<=300))])))
print("표준편차 지출금액 : {}".format(round(np.std(np.arange(min,max,.1)),3)))

평균 지출금액 : 162.5
표준편차 지출금액 : 79.386

 

2> 무작위로 한 사람 선정, 이사람이 연간 150만원 이상 지출할 확률

 

P(X>=150) = 1- P(X<150) = 0.545

 

fig = plt.figure(figsize= (15,8))

ax = sns.lineplot(x= x , y= y)

ax.hlines(y= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , xmin = min-10 , xmax  =310)
#
ax.vlines(x= 150 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')
# ax.vlines(x= 5 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')
#
ax.fill_between(x , y , 0 , where = (x>= 150)) #오차있으므로 신경 끄자.
ax.text(0-15 , 0.0034 , "y = {}".format(round(scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min),7)), fontsize =  14)
#
#area = 1- P(25<=X<150)
area = 1- (scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) *(150-25))
#
#
ax.text(95 ,0.0034 , "P(X>=150) = {}".format(round(area,3)), fontsize =  14)

==> x축의 시작이 25부터 인점 주목하자!!!!!

균등분포_5

 

3> 무작위로 한 사람 선정, 이사람이 연간 50만원 이상 , 150만원 이하로 지출할 확률

 

 

P(50<=X<=150) = P(X<=150) - P(X<=50) = 0.3636

 

fig = plt.figure(figsize= (15,8))

ax = sns.lineplot(x= x , y= y)

ax.hlines(y= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , xmin = min-10 , xmax  =310)
#
ax.vlines(x= 150 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')
ax.vlines(x= 50 , ymin = 0 ,ymax= scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) , color ='black')
#
ax.fill_between(x , y , 0 , where = (x<= 150) & (x>=50)) #오차있으므로 신경 끄자.
ax.text(0-15 , 0.0034 , "y = {}".format(round(scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min),7)), fontsize =  14)
#
#area = P(X<=150) - P(X<=50)
area = (scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) *(150-25)) - (scipy.stats.uniform.pdf(x=30 , loc= min , scale = max-min) *(50-25))
#
#
ax.text(155 ,0.0034 , "P(50<=X<=150) = {}".format(round(area,4)), fontsize =  14)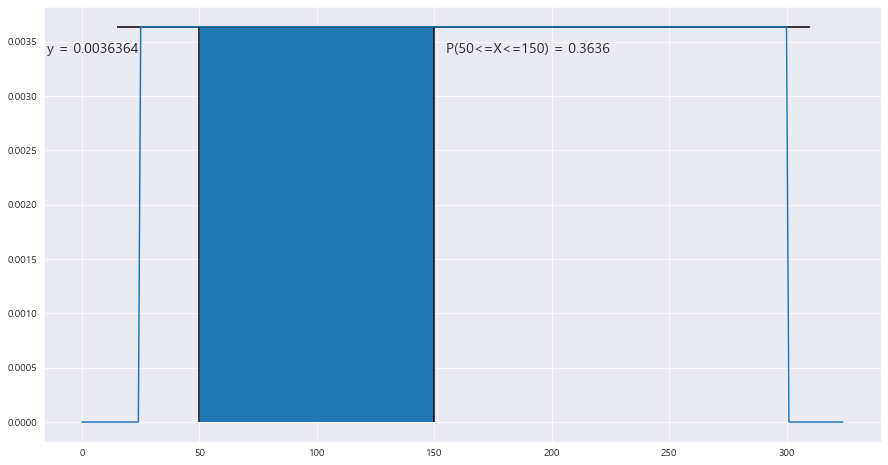

균등분포_6

출처 :  [쉽게 배우는 생활속의 통계학]  [북스힐 , 이재원] 

※혼자 공부 정리용