★산점도 그래프★이변량 양적자료★기초통계학-[Chapter02 - 03]
2022. 11. 30. 13:58
728x90
반응형
EX) 경쟁관계에 있는 두 고등학교 학생들의 학업 능력, 여성 근로자와 남성 근로자의 생산량과 같이 서로 비교되는 두 자료 집단의 관찰값 비교
==> 점도표 , 도수다각형 또는 줄기-잎 그림을 사용하면 편리하다.
산점도
두 종류의 자료가 독립변수, 응답변수의 관계
수평축에 독립변수 x를 , 수직축에 응답변수 y를 기입하여 순서쌍 (x,y)를 점으로 나타낸 그림이다.
a = pd.DataFrame({'팀' : ['뉴욕' , '토론토' , '볼티모어' , '보스턴' , '템파베이' , '클리브랜드' , '디트로이트' ,
'시카고' , '켄자스시티' , '미네소타' , '애너하임' , '텍사스' , '시애틀' , '오클랜드'],
'승리한 경기수' : [103,78,67,93,55,74,55,81,62,94,99,72,93,103],
'평균타율' : [0.275,0.261,0.246,0.277,0.253,0.249,0.248,0.268,0.256,0.272,0.282,0.269,0.275,0.261]})
a
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.scatter(a['승리한 경기수'], a['평균타율'])
plt.xlabel('승리한 경기 수(개)')
plt.ylabel('평균 타율')
plt.show()
==> 산점도로부터, 승리한 경기 수가 많을 수록 평균 타율이 높고,
승리한 경기 수가 적을수록 타율이 낮다는 결론을 얻을 수 있다.
b = pd.DataFrame({'전용면적(m**2)' : [93.75,84.88,44.33,59.82,116.46,41.30,45.90,41.30,41.30,49.94,58.01,58.01,41.30,41.30,45.77,41.30,41.30,58.01,60.50,59.20,31.98,59.28,41.30,45.77,49.94,31.95,38.52,45.90] ,
'실거래가 가격(만원)' : [40800,44000,16600,28800,35300,17500,16900,14000,16900,18600,21400,22500,15750,14000,14750,17300,17700,25300,21800,23100,17150,27000,20000,18900,22800,16000,23000,16000]})
b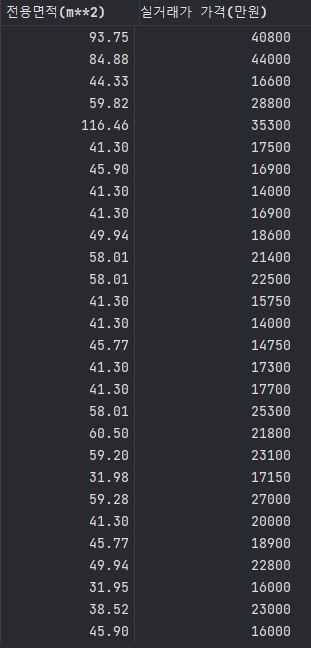
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.scatter(b['전용면적(m**2)'], b['실거래가 가격(만원)'])
plt.xlabel('전용면적(m**2)')
plt.ylabel('실거래가 가격(만원)')
plt.show()
==> 산점도로부터, 전용면적이 작을수록 실거래가 가격이 낮음을 알 수 있다.
==> 산점도의 경우 독립변수(x) 와 응답변수(y)의 값이 모두 양적변수여야 한다.
https://knowallworld.tistory.com/189
==> 재외공관 코드와 단수_복수_합계로 그래프를 그릴 수 없다.
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
728x90
반응형
'기초통계 > 막대그래프,히스토그램' 카테고리의 다른 글
| ★Pie Chart[Python]★기초통계학-[Chapter02 - 연습문제_03] (0) | 2022.12.01 |
|---|---|
| Plt, Fig, Seaborn 이해[Python]★기초통계학-[Chapter02 - 연습문제_02] (0) | 2022.11.30 |
| ★zip, collections.Counter()★도수표, 도수막대그래프★Plt, Fig, Seaborn 이해[Python]★기초통계학-[Chapter02 - 연습문제] (0) | 2022.11.30 |
| ★양적자료의 요약★점도표, 도수분포표 , 특이점,계급 , 계급의 수★도수히스토그램★기초통계학-[Chapter02 - 02] (0) | 2022.11.29 |
| ★질적자료의 요약★seaborn, matplotlib★기초통계학-[Chapter02 - 01] (0) | 2022.11.29 |