★최소분산불편추정량★편의추정량★불편추정량★점추정량★기초통계학-[연습문제 -08]
4. 모분산이 4인 정규모집단에서 크기 3인 확률표본을 선정하여 모평균을 추정하기 위해 다음과 같이 점추정량을 설정하였다.
^m_1 = (1/3)*(X_1 + X_2 + X_3) , ^m_2 = (1/4)*(X_1+ X_2 + 2*X_3) , ^m_3 = (1/3) * (3*X_1 + X_2 +X_3)
https://knowallworld.tistory.com/324
★편의 추정량★불편 추정량★기초통계학-[대표본 추정 -01]
1. 점추정 ==> 임의의 모집단으로부터 대표본을 추출하면 중심극한정리에 의해 표본평균은 정규분포에 근사한다. https://knowallworld.tistory.com/304 ★중심극한정리★기초통계학-[모집단 분포와 표본
knowallworld.tistory.com
1> 각 추정량의 편의를 구하라.
E(^m_1) = (1/3)E(X_1 + X_2 + X_3) = (1/3)*(m + m + m) = m ==> 불편추정량
E(^m_2) = (1/4)E(X_1 + X_2 + 2* X_3) = (1/4) * (m+ m +2*m) = m ==>불편추정량
E(^m_3) = (1/3)E(3* X_1 + X_2 + X_3) = (1/3) *( 3*m + m +m) = (5/3)m ==> 편의추정량

2> 불편추정량의 분산을 구하고, 최소분산불편추정량을 구하라.
https://knowallworld.tistory.com/325
★불편추정량★최소분산불편추정량★유효 추정량★불편 추정량★기초통계학-[대표본 추정 -02]
1. 유효추정량 ==> 일반적으로 절사평균은 모평균에 대한 불편추정량이 아니다. https://knowallworld.tistory.com/213 np.median★절사평균, 중위수★기초통계학-[Chapter03 - 03] 1. 절사평균 A = [1,2,3,4,5] 의 산술
knowallworld.tistory.com
Var(^m_1) = (1/9)Var(X_1 + X_2 + X_3) = (1/9)(4+4+4) = 4/3
Var(^m_2) = (1/16)Var(X_1 + X_2 + 4*X_3) = (1/16) ( 4 + 4 + 16) = (24/16) = 3/2
Var(^m_1) < Var(^m_2)
==> 최소분산불편추정량은 ^m_1 이다.
5. 모분산이 4인 정규모집단에서 크기 3인 확률표본을 선정하여 모평균을 추정하기 위해 다음과 같이 점추정량을 설정하였다.
^m_1 = (1/2)X_1 + (1/3)X_2 + (1/6)X_3
^m_2 = (1/2)X_1 + (1/3)X_2 + (1/4)X_3
^m_3 = (1/3)X_1 + (1/4)X_2 + (5/12)X_3
1> 각 추정량의 편의를 구하라.
E(^m_1) = (1/6)(3m + 2m + 1m) = m ==> 불편추정량
E(^m_2) = (1/12)(6m + 4m + 3m) = 13/12 m ==> 편의추정량
E(^m_3) = (1/12)(4m + 3m + 5m) = m ==> 불편추정량
2> 불편추정량의 분산을 구하고, 최소분산불편추정량을 구하라.
Var(^m_1) = Var( (1/6) * (9X_1 + 4X_2 + X_3) ) = (1/36) * (36 + 16 + 4) = 56/36 = 14/9
Var(^m_3) = (1/144) (16*4 + 9*4 +25*4) = (64 +36 +100) / 144 = 200/144 = 25/18
Var(^m_3) < Var(^m_1)
==> 최소분산불편추정량은 ^m_3
6. 모분산이 8인 정규모집단에서 크기 50인 표본을 조사한결과 모두 더한값이 426.8이 었다. 결과를 이용하여 모평균에 대한 95%신뢰구간을 구하라.
n = 50
모분산 = 8
z_0.025 = 1.96
|X = 426.8/50
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰도
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)
STDS = round(math.sqrt(8),3) #모표준편차
n = 50
MEANS = round(426.8/ 50,3)
ax.text(2 , .35, r'$\overline{X}$ = ' +f'{MEANS}\n'+ r'$\sigma = $' + f'{STDS}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(n),3)}',fontsize=15)
ax.text(2 , .3, r'신뢰구간 L = $2*{%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 + f'{round(2* z_1 * STDS / math.sqrt(n),3)}',fontsize=15)
ax.text(-5.5 , .3, r'신뢰구간 = $\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$' +f'= ({round(MEANS - z_1 * STDS/math.sqrt(n),3)} , {round(MEANS + z_1*STDS/math.sqrt(n),3)})',fontsize=15)
ax.text(2 , .25, r'오차한계 = ${%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 + f'{round(z_1 * STDS / math.sqrt(n),3)}',fontsize=15)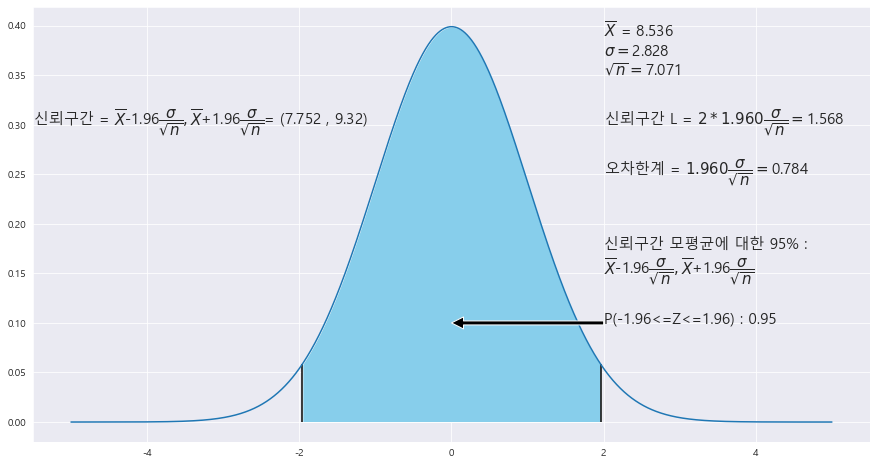
신뢰구간 = (7.752 , 9.32)
7. 어느 회사에서 생산하는 비누의 무게는 분산이 5.4g인 정규분포를 따른다고 한다. 50개의 비누를 임의로 추출하였을 때 그 평균 무게의 값은 95.1g 이었다. 이 회사에서 생산하는 비눈의 평균 무게에 대한 95% 신뢰구간을 구하라.
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰도
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)
STDS = round(math.sqrt(5.4),3) #모표준편차
n = 50
MEANS = 95.1
ax.text(2 , .35, r'$\overline{X}$ = ' +f'{MEANS}\n'+ r'$\sigma = $' + f'{STDS}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(n),3)}',fontsize=15)
ax.text(2 , .3, r'신뢰구간 L = $2*{%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 + f'{round(2* z_1 * STDS / math.sqrt(n),3)}',fontsize=15)
ax.text(-5.5 , .3, r'신뢰구간 = $\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$' +f'= ({round(MEANS - z_1 * STDS/math.sqrt(n),3)} , {round(MEANS + z_1*STDS/math.sqrt(n),3)})',fontsize=15)
ax.text(2 , .25, r'오차한계 = ${%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 + f'{round(z_1 * STDS / math.sqrt(n),3)}',fontsize=15)
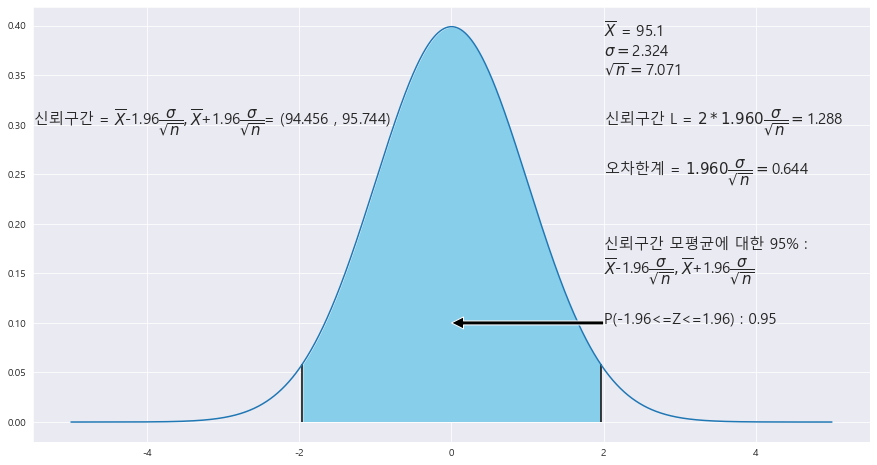
신뢰구간 = (94.456 , 95.744)
8. 어느 직장에 근무하는 직원 20명에 대한 혈중 콜레스테롤 수치를 조사한 자료이다. 이 직장에 근무하는 직원들의 콜레스테롤 수치는 분산이 400인 정규분포를 따른다고 할때, 평균 콜레스테롤에 대한 95% 신뢰구간을 구하라.
A = [193.27, 193.88, 253.26, 237.15, 188.83, 200.56, 274.31, 230.36, 212.08, 222.19, 198.48, 202.5, 215.35, 218.95, 233.16, 222.23, 218.53, 204.64, 206.72, 199.37]
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰도
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)
A = "193.27 193.88 253.26 237.15 188.83 200.56 274.31 230.36 212.08 222.19 198.48 202.50 215.35 218.95 233.16 222.23 218.53 204.64 206.72 199.37"
A = list(map(float, A.split()))
STDS = round(math.sqrt(400) , 2) #모표준편차
n = len(A)
MEANS = np.mean(A)
ax.text(2 , .35, r'$\overline{X}$ = ' +f'{MEANS}\n'+ r'$\sigma = $' + f'{STDS}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(n),3)}',fontsize=15)
ax.text(2 , .3, r'신뢰구간 L = $2*{%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 + f'{round(2* z_1 * STDS / math.sqrt(n),3)}',fontsize=15)
ax.text(-5.5 , .3, r'신뢰구간 = $\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$' +f'= ({round(MEANS - z_1 * STDS/math.sqrt(n),3)} , {round(MEANS + z_1*STDS/math.sqrt(n),3)})',fontsize=15)
ax.text(2 , .25, r'오차한계 = ${%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 + f'{round(z_1 * STDS / math.sqrt(n),3)}',fontsize=15)
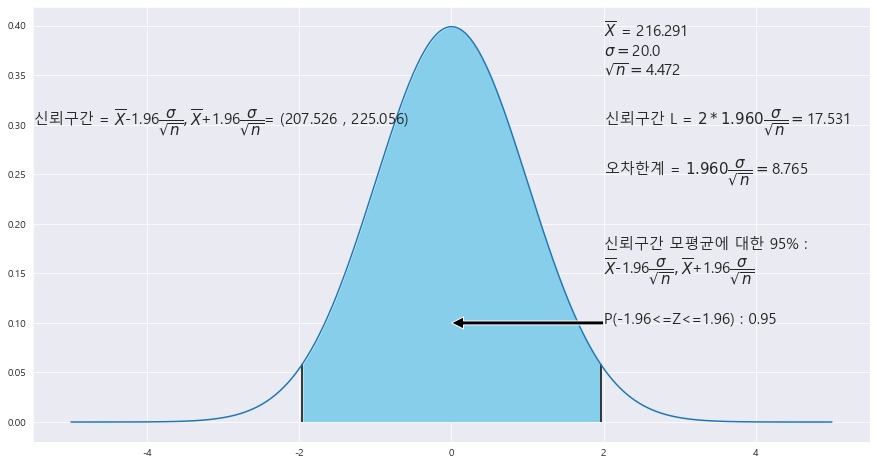
신뢰구간 = (207.526 , 225.056)
9. 종업원이 제공하는 서비스 시간에 대한 자료이다. 과거 경험에 따르면 서비스 시간이 표준편차 25초인 정규분포를 따른다고 한다. 이때 평균 서비스 시간에 대한 95% 신뢰구간을 구하라.
A = [95.0, 21.0, 54.0, 127.0, 109.0, 51.0, 65.0, 30.0, 98.0, 107.0, 68.0, 99.0, 69.0, 101.0, 73.0, 82.0, 100.0, 63.0, 45.0, 76.0, 72.0, 85.0, 121.0, 76.0, 117.0, 67.0, 126.0, 112.0, 83.0, 95.0]
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰도
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)
A = "95 21 54 127 109 51 65 30 98 107 68 99 69 101 73 82 100 63 45 76 72 85 121 76 117 67 126 112 83 95"
A = list(map(float, A.split()))
print(len(A))
print(A)
STDS = round(math.sqrt(25**2) , 2) #모표준편차
n = len(A)
MEANS = np.mean(A)
ax.text(2 , .35, r'$\overline{X}$ = ' +f'{MEANS}\n'+ r'$\sigma = $' + f'{STDS}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(n),3)}',fontsize=15)
ax.text(2 , .3, r'신뢰구간 L = $2*{%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 + f'{round(2* z_1 * STDS / math.sqrt(n),3)}',fontsize=15)
ax.text(-5.5 , .3, r'신뢰구간 = $\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$' +f'= ({round(MEANS - z_1 * STDS/math.sqrt(n),3)} , {round(MEANS + z_1*STDS/math.sqrt(n),3)})',fontsize=15)
ax.text(2 , .25, r'오차한계 = ${%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 + f'{round(z_1 * STDS / math.sqrt(n),3)}',fontsize=15)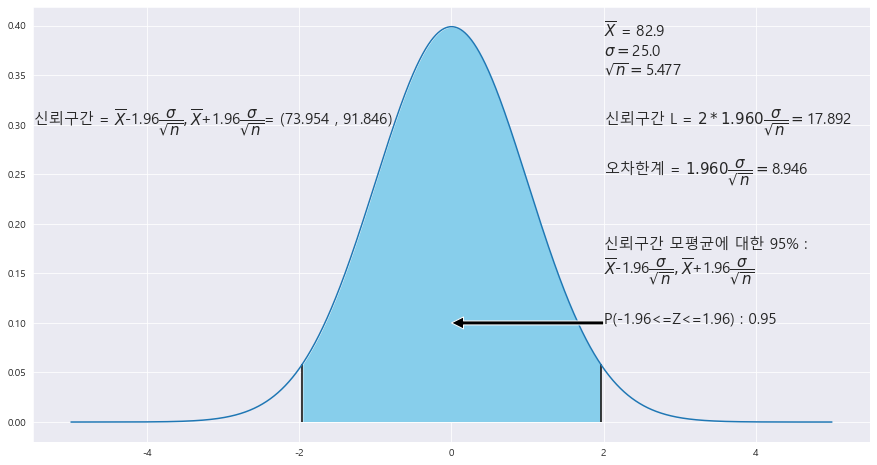
신뢰구간 = (73.954 , 91.846)
10. TV 광고 시간을 측정한 자료이다. 이 자료를 이용하여 TV평균 시간에 대한 95% 근사 신뢰구간을 구하라.(표준편차가 0.22분인 정규분포를 따른다.)
A = [1.5, 2.9, 2.8, 1.6, 2.2, 2.5, 1.9, 2.0, 3.1, 2.7, 1.3, 1.9, 2.6, 1.9, 2.7, 1.8, 1.7, 2.2, 2.3, 2.3, 3.5, 1.8, 1.5, 2.1, 2.0, 1.5, 2.0, 2.4, 1.9, 2.3]
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰도
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$',fontsize=15)
A = "1.5 2.9 2.8 1.6 2.2 2.5 1.9 2.0 3.1 2.7 1.3 1.9 2.6 1.9 2.7 1.8 1.7 2.2 2.3 2.3 3.5 1.8 1.5 2.1 2.0 1.5 2.0 2.4 1.9 2.3"
A = list(map(float, A.split()))
print(len(A))
print(A)
STDS = round(math.sqrt(0.22**2) , 2) #모표준편차
n = len(A)
MEANS = np.mean(A)
ax.text(2 , .35, r'$\overline{X}$ = ' +f'{MEANS}\n'+ r'$\sigma = $' + f'{STDS}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(n),3)}',fontsize=15)
ax.text(2 , .3, r'신뢰구간 L = $2*{%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 + f'{round(2* z_1 * STDS / math.sqrt(n),3)}',fontsize=15)
ax.text(-5.5 , .3, r'신뢰구간 = $\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$' +f'= ({round(MEANS - z_1 * STDS/math.sqrt(n),3)} , {round(MEANS + z_1*STDS/math.sqrt(n),3)})',fontsize=15)
ax.text(2 , .25, r'오차한계 = ${%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 + f'{round(z_1 * STDS / math.sqrt(n),3)}',fontsize=15)
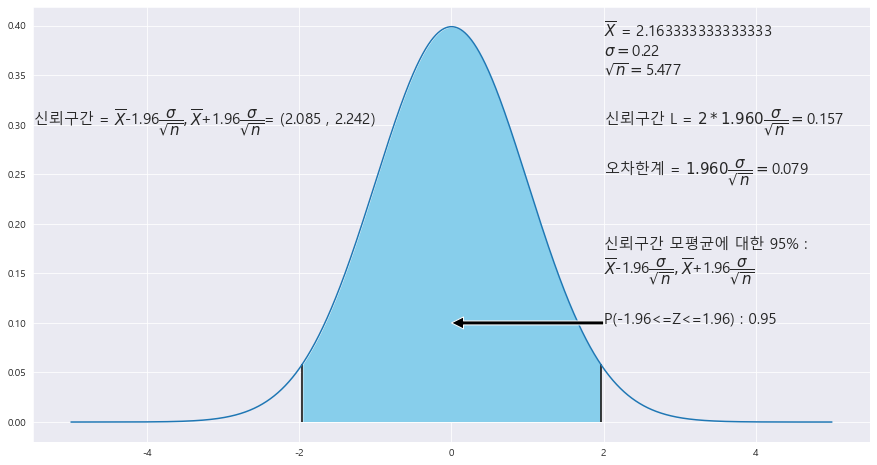
신뢰구간 : (2.085 , 2.242)
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 대표본 추정' 카테고리의 다른 글
| ★모평균 , 모비율의 차에 대한 신뢰구간★모비율에 대한 오차한계 및 신뢰구간★기초통계학-[연습문제 -10] (0) | 2023.01.12 |
|---|---|
| ★모평균, 모비율간 차에 대한 오차한계 및 신뢰구간★두 모평균,모비율의 차에 대한 점추정★기초통계학-[연습문제 -09] (0) | 2023.01.12 |
| ★모비율,모평균에 대한 오차한계★오차한계(신뢰구간의 절반)★기초통계학-[연습문제 -07] (0) | 2023.01.12 |
| ★모평균의 차에 대한 신뢰구간★모비율에 대한 표본크기 구하기★표본의 크기★기초통계학-[대표본 추정 -06] (0) | 2023.01.12 |
| ★string r'로 받을때 안에 값 집어넣기(변수로도 %2d)★모비율 차의 구간추정★기초통계학-[대표본 추정 -06] (0) | 2023.01.11 |