★모평균, 모비율간 차에 대한 오차한계 및 신뢰구간★두 모평균,모비율의 차에 대한 점추정★기초통계학-[연습문제 -09]
11. 모분산이 각각 9, 4 이고 서로 독립인 두 정규모집단으로부터 각각 크기 25와 36인 표본을 추출하여 표본평균 35 , 32.5를 얻었다.
https://knowallworld.tistory.com/307
★두 표본평균의 차에 대한 표본분포(모분산 알때 , 동일할때)★중심극한정리 활용★이표본의
1. 이표본의 표본분포 ==>지금까지는 단일 모집단의 표본에 대한 통계량의 표본분포 EX) 수능에서 남학생, 여학생 집단의 평균이 동일한지 여부 비교 ==> 비교위해서는 각각 표본을 추출하여야 한
knowallworld.tistory.com
==> 모평균(표본평균)간 차에 대한 정규분포
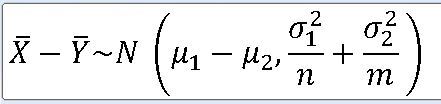
1> 두 모평균 차를 점추정
|X - |Y = 35 - 32.5 = 2.5
2> |X - |Y의 표준오차를 구하라.
3> | (|X - |Y) - (뮤_1 -뮤_2)| 에 대한 95%의 오차한계를 구하라.
4> 두 모평균 차에 대한 95%신뢰구간을 구하라.
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95#신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(-5.5 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\left( \overline{x}-\overline{y}\right)$' +f'-{z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$' +' , '+ r'$\left( \overline{x}-\overline{y}\right)$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$',fontsize=15)
MEANS_A = 35
MEANS_B = 32.5
Var_A = 9
Var_B = 4
STDS_A = round(math.sqrt(Var_A),2)
STDS_B = round(math.sqrt(Var_B) , 2)
n_A = 25
n_B = 36
ax.text(-5.5 , .2 , f'표준오차 :' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$' + f'= {round(math.sqrt(Var_A/n_A + Var_B/n_B),3)}' , fontsize = 15)
ax.text(2 , .35, r'$\overline{X}_{1}$ = ' +f'{MEANS_A}'+ r' , $\overline{X}_{2}$ = ' +f'{MEANS_B}\n' + r'$\sigma_{1} = $' + f'{STDS_A}' + r', $\sigma_{2} = $' + f'{STDS_B}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(n_A),3)}' + r', $\sqrt{m} = $' + f'{round(math.sqrt(n_B),3)}',fontsize=15)
b = r'N($\overline{X}-\overline{Y} = $' + f'{MEANS_A - MEANS_B}, ' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$ = '+f'{round(math.sqrt(Var_A/n_A + Var_B/n_B) , 3)})'
plt.legend([b] , fontsize = 15 , loc='upper left')
ax.text(-5.5 , .15, r'오차한계 = ${%.3f}\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}} = $' % z_1 + f'{z_1 * round(math.sqrt(Var_A/n_A + Var_B/n_B) , 3)}',fontsize=15)
ax.text(2 , .25, f'모평균의 차에 대한 신뢰구간 {trust}% , \n' + r'신뢰구간 L = $2*{%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 +f': \n' + f'({round((MEANS_A-MEANS_B) - (z_1)*math.sqrt(Var_A/n_A + Var_B/n_B),3)} ~ {round((MEANS_A-MEANS_B) + (z_1)*math.sqrt(Var_A/n_A + Var_B/n_B),3)})' , fontsize= 15)
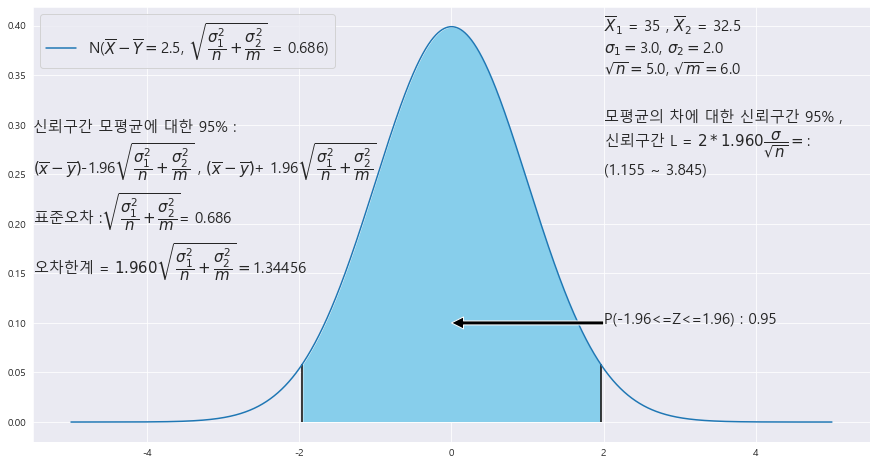
표준오차 = 0.686
오차한계 = 1.344
신뢰구간 =
(1.155 , 3.845)
==> 표준정규분포와 기존데이터의 정규분포표 같이 그려보자.
12. 남성과 여성의 펴균 주급에 차이가 있는지 조사하기 위해 미국에서 조사한 결과 전일제 임금근로자인 남성 256명의 평균 주급은 854달러, 여성 162명의 평균 주급은 691달러 였다. 이때 남성의 표준편차는 121달러이고, 여성의 표준편차는 86달러인 정규분포를 따른다고 한다.
1> 남성과 여성의 평균 주급의 차를 점추정
|X - |Y = 854 - 691 = 163
2> |X - |Y의 표준오차를 구하라.
3> | (|X - |Y) - (뮤_1 -뮤_2)| 에 대한 95%의 오차한계를 구하라.
4> 두 모평균 차에 대한 95%신뢰구간을 구하라.
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95#신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(-5.5 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\left( \overline{x}-\overline{y}\right)$' +f'-{z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$' +' , '+ r'$\left( \overline{x}-\overline{y}\right)$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$',fontsize=15)
MEANS_A = 854
MEANS_B = 691
Var_A = 121**2
Var_B = 86**2
STDS_A = round(math.sqrt(Var_A),2)
STDS_B = round(math.sqrt(Var_B) , 2)
n_A = 256
n_B = 162
ax.text(-5.5 , .2 , f'표준오차 :' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$' + f'= {round(math.sqrt(Var_A/n_A + Var_B/n_B),3)}' , fontsize = 15)
ax.text(2 , .35, r'$\overline{X}_{1}$ = ' +f'{MEANS_A}'+ r' , $\overline{X}_{2}$ = ' +f'{MEANS_B}\n' + r'$\sigma_{1} = $' + f'{STDS_A}' + r', $\sigma_{2} = $' + f'{STDS_B}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(n_A),3)}' + r', $\sqrt{m} = $' + f'{round(math.sqrt(n_B),3)}',fontsize=15)
b = r'N($\overline{X}-\overline{Y} = $' + f'{MEANS_A - MEANS_B}, ' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$ = '+f'{round(math.sqrt(Var_A/n_A + Var_B/n_B) , 3)})'
plt.legend([b] , fontsize = 15 , loc='upper left')
ax.text(-5.5 , .15, r'오차한계 = ${%.3f}\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}} = $' % z_1 + f'{z_1 * round(math.sqrt(Var_A/n_A + Var_B/n_B) , 3)}',fontsize=15)
ax.text(2 , .25, f'모평균의 차에 대한 신뢰구간 {trust}% , \n' + r'신뢰구간 L = $2*{%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 +f': \n' + f'({round((MEANS_A-MEANS_B) - (z_1)*math.sqrt(Var_A/n_A + Var_B/n_B),3)} ~ {round((MEANS_A-MEANS_B) + (z_1)*math.sqrt(Var_A/n_A + Var_B/n_B),3)})' , fontsize= 15)
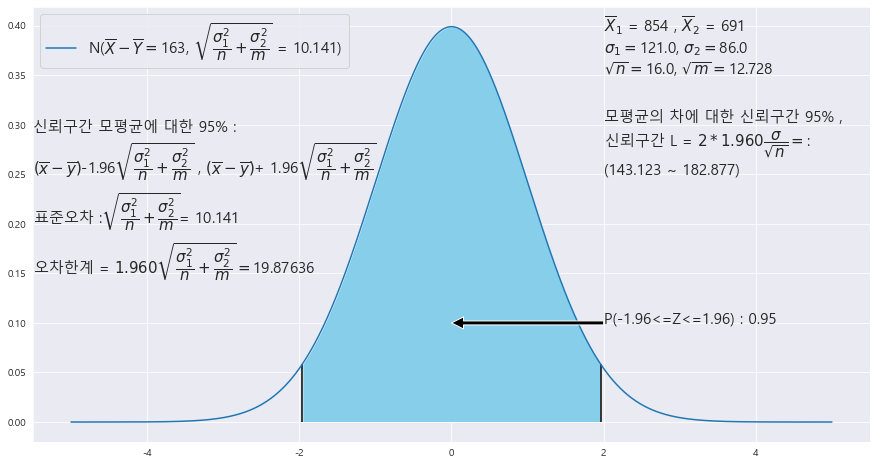
표준오차 = 10.141
오차한계 = 19.87636
신뢰구간 = (143.123 , 182.877)
13. 금융감독원이 2010년도에 전국 28개 대학의 2490명의 학생을 대상으로 대학생 금융 이해력 평가를 실시하여 총점 100점에 대해 다음 결과를 얻었다.
1> 2490명의 평균 점수는 60.8점이다. 전체 대학생의 점수는 표준편차가 10.5점인 정규분포를 따른다고 할 때, 우리나라 대학생의 금융 이해력의 평균 점수에 대한 95% 신뢰구간을 구하라.
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰도
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
MEANS = 60.8
STDS = round(math.sqrt(10.5**2),3) #모표준편차
n = 2490
ax.text(-5.5 , .35, r'$\overline{X} = $'+f'{MEANS}\n' + r'$\sigma = $' + f'{STDS}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(n),3)}',fontsize=15)
ax.text(-5.5 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\overline{X}$' +f'-{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}},\overline{X}$' + f'+{z_1}' + r'$\dfrac{\sigma}{\sqrt{n}}$ = ' + f'({round(MEANS - z_1*STDS/math.sqrt(n),2)} , {round(MEANS + z_1*STDS/math.sqrt(n),2)})',fontsize=15)
ax.text(-5.5 , .25, r'신뢰구간 L = $2*{%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 + f'{round(2* z_1 * STDS / math.sqrt(n),3)}',fontsize=15)
ax.text(-5.5 , .3, r'오차한계 = ${%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 + f'{round(z_1 * STDS / math.sqrt(n),3)}',fontsize=15)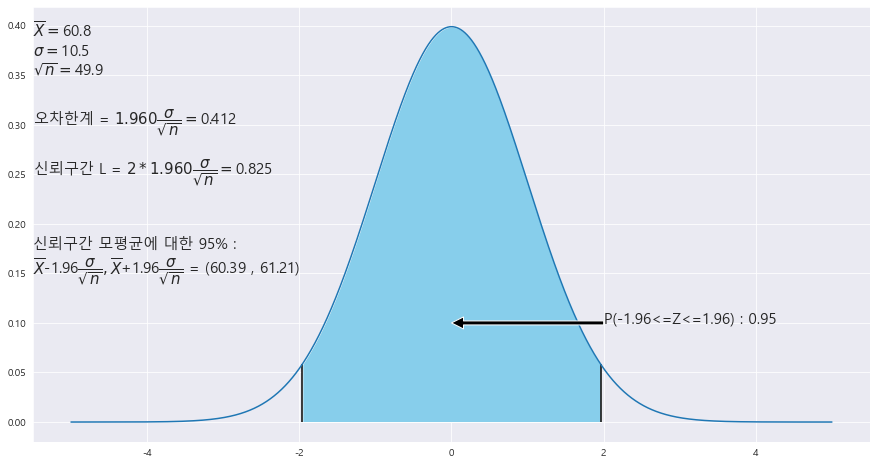
신뢰구간 = (60.39 , 61.21)
2> 상경계열 평균은 65.7점이고, 공학계열 평균은 49.5점이었다. 상경계열 학생 356명과 공학계열 학생 324명을 조사하였고 각각 분산이 21과 85인 정규분포를 따른다고 할 때, 상경계열과 공학계열 학생의 평균 점수의 차에 대한 95% 신뢰구간을 구해라.
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95#신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
ax.text(-5.5 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\left( \overline{x}-\overline{y}\right)$' +f'-{z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$' +' , '+ r'$\left( \overline{x}-\overline{y}\right)$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$',fontsize=15)
MEANS_A = 65.7
MEANS_B = 49.5
Var_A = 21
Var_B = 85
STDS_A = round(math.sqrt(Var_A),2)
STDS_B = round(math.sqrt(Var_B) , 2)
n_A = 356
n_B = 324
ax.text(-5.5 , .2 , f'표준오차 :' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$' + f'= {round(math.sqrt(Var_A/n_A + Var_B/n_B),3)}' , fontsize = 15)
ax.text(2 , .35, r'$\overline{X}_{1}$ = ' +f'{MEANS_A}'+ r' , $\overline{X}_{2}$ = ' +f'{MEANS_B}\n' + r'$\sigma_{1} = $' + f'{STDS_A}' + r', $\sigma_{2} = $' + f'{STDS_B}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(n_A),3)}' + r', $\sqrt{m} = $' + f'{round(math.sqrt(n_B),3)}',fontsize=15)
ax.text(-5.5 , .15, r'오차한계 = ${%.3f}\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}} = $' % z_1 + f'{round(z_1 * math.sqrt(Var_A/n_A + Var_B/n_B) , 3)}',fontsize=15)
ax.text(2 , .25, f'모평균의 차에 대한 신뢰구간 {trust}% , \n' + r'신뢰구간 L = $2*{%.3f}\dfrac{\sigma}{\sqrt{n}} = $' % z_1 +f': \n' + f'({round((MEANS_A-MEANS_B) - (z_1)*math.sqrt(Var_A/n_A + Var_B/n_B),3)} ~ {round((MEANS_A-MEANS_B) + (z_1)*math.sqrt(Var_A/n_A + Var_B/n_B),3)})' , fontsize= 15)
b = r'N($\overline{X}-\overline{Y} = $' + f'{round(MEANS_A - MEANS_B ,2)}, ' + r'$\sqrt{\dfrac{\sigma_{1}^{2}}{n}+\dfrac{\sigma_{2} ^{2}}{m}}$ = '+f'{round(math.sqrt(Var_A/n_A + Var_B/n_B) , 3)})'
plt.legend([b] , fontsize = 15 , loc='upper left')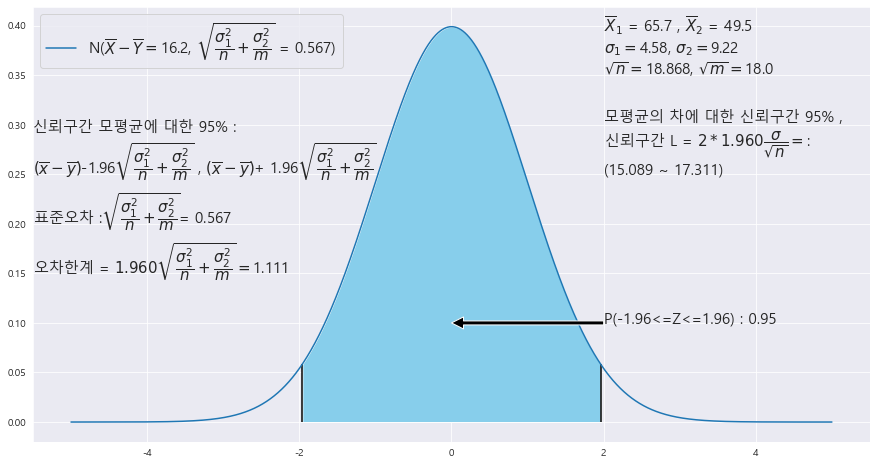
평균 점수의 차에 대한 95% 신뢰구간 (15.089 , 17.311)
14. 서울시의 어느 중학교에서는 반바지 교복 착용에 대해 전교생 720명을 대상으로 설문 조사한 결과, 97%의 찬성률로 반바지 교복을 착용하고 있다.
1> 전체 중학생의 찬성률을 점추정
^p = 0.97
2> 표본비율 ^p의 표준오차를 구하라.
3> 95% 오차한계 구하라.
4> 찬성률에 대한 95% 신뢰구간을 구하라.
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 95 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
# print((z_1 * STDS / math.sqrt(len(A))))
# STDS = round(math.sqrt(4),3) #모표준편차
RATIO = 0.97
n = 720
ax.text(2 , .35, r'$\sqrt{\widehat{p}\widehat{q}} = $' + f'{round(math.sqrt(RATIO * (1-RATIO)),3)}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(n),2)}',fontsize=15)
ax.text(2 , .3, r'신뢰구간 L = $2*{%.3f}\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}} = $' % z_1 + f'{round(2* z_1 * math.sqrt(RATIO * (1-RATIO) / n),3)}',fontsize=15)
ax.text(2 , .25, r'오차한계 = ${%.3f}\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}} = $' % z_1 + f'{round( z_1 * math.sqrt(RATIO * (1-RATIO) / n),3)}',fontsize=15)
ax.text(-5.5 , .35, r'표준오차 = $\dfrac{\sigma}{\sqrt{n}} = $' + f'{round( math.sqrt(RATIO * (1-RATIO) / n),3)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$(\widehat{p}$' +f'-{z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$' +' , '+ r'$\widehat{p}$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}})$ = ' + f'({round(RATIO - z_1*math.sqrt(RATIO*(1-RATIO) /n),2)} , {round(RATIO + z_1*math.sqrt(RATIO*(1-RATIO) /n),2)})' ,fontsize=15)
print(z_1)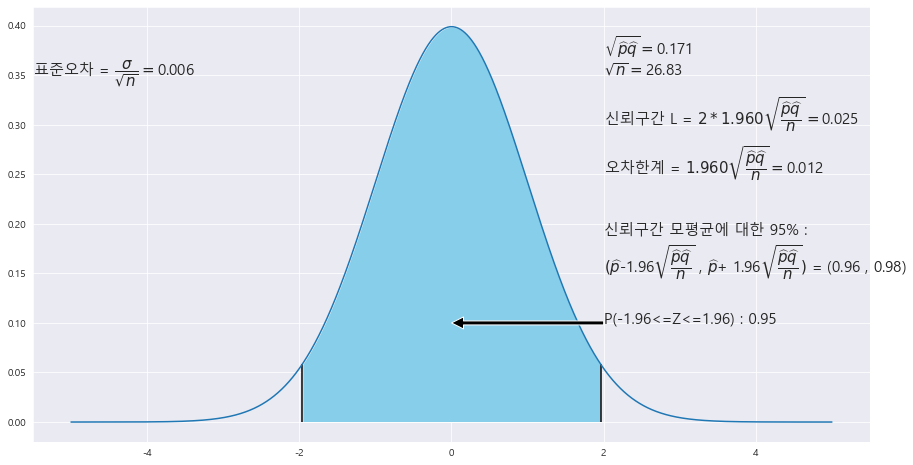
표준오차 = 0.006
오차한계 = 0.012
신뢰구간 = (0.96 , 0.98)
15. 2014년에 서울지역 자가 운전자 1000명을 대상으로 설문 조사를 실시한 결과, 가짜 석유 경험있는 소비자가 79.3%에 이른다. 이와 같은 경험을 가진 서울 지역 자가 운전자의 비율에 대한 90% 신뢰구간을 구하라.
n = 1000
p = 0.793
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
trust = 90 #신뢰구간
# z_1 = round((0.05) / math.sqrt( 0.0018532 ) ,2)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=z_1) & (x>=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(z_1) - scipy.stats.norm.cdf(-z_1)
plt.annotate('' , xy=(0, .1), xytext=(2 , .1) , arrowprops = dict(facecolor = 'black'))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.text(2 , .1, f'P({-z_1}<=Z<={z_1}) : {round(area,4)}',fontsize=15)
# print((z_1 * STDS / math.sqrt(len(A))))
# STDS = round(math.sqrt(4),3) #모표준편차
RATIO = 0.793
n = 1000
ax.text(2 , .35, r'$\sqrt{\widehat{p}\widehat{q}} = $' + f'{round(math.sqrt(RATIO * (1-RATIO)),3)}\n' + r'$\sqrt{n} = $' + f'{round(math.sqrt(n),2)}',fontsize=15)
ax.text(2 , .3, r'신뢰구간 L = $2*{%.3f}\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}} = $' % z_1 + f'{round(2* z_1 * math.sqrt(RATIO * (1-RATIO) / n),3)}',fontsize=15)
ax.text(2 , .25, r'오차한계 = ${%.3f}\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}} = $' % z_1 + f'{round( z_1 * math.sqrt(RATIO * (1-RATIO) / n),3)}',fontsize=15)
ax.text(-5.5 , .35, r'표준오차 = $\dfrac{\sigma}{\sqrt{n}} = $' + f'{round( math.sqrt(RATIO * (1-RATIO) / n),3)}',fontsize=15)
ax.text(2 , .15, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$(\widehat{p}$' +f'-{z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}}$' +' , '+ r'$\widehat{p}$' +f'+ {z_1}' + r'$\sqrt{\dfrac{\widehat{p}\widehat{q}}{n}})$ = ' + f'({round(RATIO - z_1*math.sqrt(RATIO*(1-RATIO) /n),2)} , {round(RATIO + z_1*math.sqrt(RATIO*(1-RATIO) /n),2)})' ,fontsize=15)
print(z_1)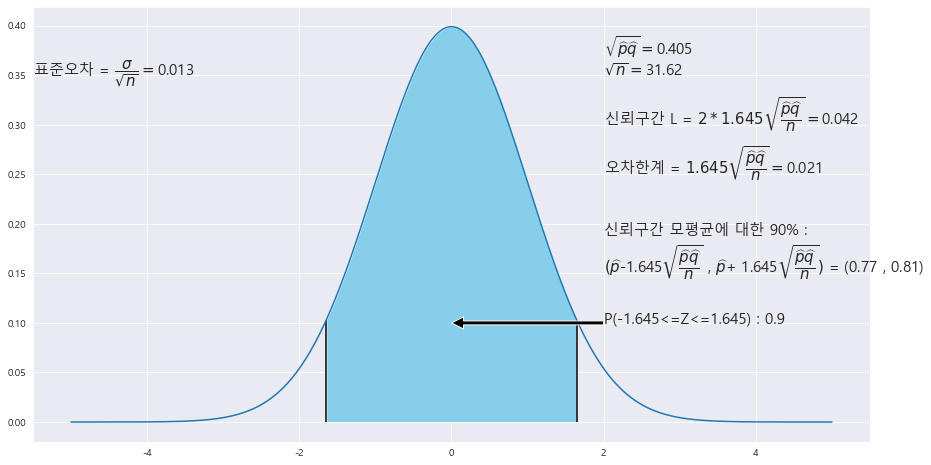
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 대표본 추정' 카테고리의 다른 글
| ★비율을 알고 있을때와 모를때의 표본의 크기★모표준편차 1개가 주어질때 표본의 크기 구하기★모비율의 차에 대한 신뢰구간★기초통계학-[연습문제 -11] (0) | 2023.01.12 |
|---|---|
| ★모평균 , 모비율의 차에 대한 신뢰구간★모비율에 대한 오차한계 및 신뢰구간★기초통계학-[연습문제 -10] (0) | 2023.01.12 |
| ★최소분산불편추정량★편의추정량★불편추정량★점추정량★기초통계학-[연습문제 -08] (0) | 2023.01.12 |
| ★모비율,모평균에 대한 오차한계★오차한계(신뢰구간의 절반)★기초통계학-[연습문제 -07] (0) | 2023.01.12 |
| ★모평균의 차에 대한 신뢰구간★모비율에 대한 표본크기 구하기★표본의 크기★기초통계학-[대표본 추정 -06] (0) | 2023.01.12 |