★합동표본비율★양측검정, 상단측검정, 하단측검정 구분하기★모비율 차의 검정★기초통계학-[통계적 가설검정 -08]
https://knowallworld.tistory.com/334
★모평균 , 모비율의 차에 대한 신뢰구간★모비율에 대한 오차한계 및 신뢰구간★기초통계학-[
16. 2014년에 초,중,고 학생 116000명을 대상으로 우리나라 통일에 대해 조사한 결과, '통일이 필요하다' 라는 응답이 53.5%로 나타났다. 통일이 필요하다고 생각하는 초.중.고 학생의 비율에 대한 95%
knowallworld.tistory.com
https://knowallworld.tistory.com/311
★표본비율의 차에 대한 표본분포★기초통계학-[모집단 분포와 표본분포 -12]
1. 두 표본비율의 차에 대한 표본분포 ==> 서로 독립이고 모비율이 각각 p_1 , p_2인 두 모집단에서 각각 크기 n,m인 표본 선정 ==> 표본의 크기가 충분히 크다면 https://knowallworld.tistory.com/301 ★모비율
knowallworld.tistory.com

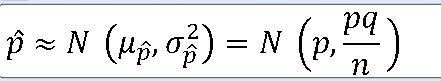
1. 합동표본비율(pooled sample proportion)
==> 두 표본에 대한 성공의 횟수 x와 y에 대한 비율
^p = (x+y)/(n+m)
==> 크기 n과 m인 표본
EX-01) 어느 대기업에 대한 취업 성향을 알아보기 위하여 20대와 30대 그룹으로 나누어 각각 952명과 1043명을 대상으로 조사하였다. 그 결과 이 기업을 선호한 인원이 각각 627명과 651명 이었다. 이 기업에 대한 20대의 선호도가 30대보다 높은지 유의수준 5%에서 검정하라.
^p_1 = 627/952
^p_2 = 651/1043
n = 952
m = 1043
20대의 선호도를 p1
30대의 선호도를 p2
p1-p2 > 0를 대립가설로 설정하면 귀무가설은 H_0 : p_1 - p_2 <=0(20대의 선호도는 30대보다 낮다) 이고, 대립가설은 H_1 : p_1-p_2 >0 이다.
귀무가설 : p_1 - p_2 <=0(20대의 선호도는 30대보다 낮다.) ==> 상단측검정
대립가설 : p_1 - p_2 > 0
1> 기각역을 구하여 검정한다.
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
# trust = 95 #신뢰도
p1 = 627/952
p2 = 651/1043
n = 952
m = 1043
ax.set_title('상단측검정' ,fontsize = 18)
#==========================================귀무가설 기각과 채택 ====================================================
trust = 95 #신뢰도_유의수준
t_1 = round(scipy.stats.norm.ppf(1-(1-(trust/100))) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=t_1) , facecolor = 'orange') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(t_1)
plt.annotate('' , xy=(0, .2), xytext=(2 , .2) , arrowprops = dict(facecolor = 'black'))
ax.text(2 , .2, r'$H_{0}$의 채택역' +f'\nP(Z<={t_1}) : {round(area,4)}',fontsize=15)
annotate_len = stats.norm.pdf(t_1, loc=0 , scale =1) /2
ax.vlines(x= t_1, ymin= 0 , ymax= stats.norm.pdf(t_1, loc=0 , scale =1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
# ax.vlines(x= -t_1, ymin= 0 , ymax= stats.norm.pdf(-t_1, loc=0 , scale =1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
area = round((1-area) ,3)
# ax.text(1 + t_1 , annotate_len+0.02 , r'$z_{\alpha} = $' + f'{t_1}\n' + r'$H_{0}$의 기각역' + f'\n'+ r'$\alpha = {%.3f}$' % area,fontsize=15)
ax.text(1.5 +t_1 , annotate_len+0.02 , r'$z_{\alpha} = $' + f'{t_1}\n' + r'$H_{0}$의 기각역' + f'\n'+ r'$\alpha = {%.3f}$' % area,fontsize=15)
# plt.annotate('' , xy=(t_1, annotate_len), xytext=(t_1+ 1 , annotate_len+0.02) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(t_1, annotate_len), xytext=(1+t_1 , annotate_len+0.02) , arrowprops = dict(facecolor = 'black'))
ax.text(-5.5 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\left(\widehat{p}_{1} - \widehat{p}_{2}\right)$' +f'-{t_1}' + r'$\sqrt{\dfrac{\widehat{p}_{1}\widehat{q}_{1}}{n}+\dfrac{\widehat{p}_{2}\widehat{q}_{2}}{m}}$' +' , \n'+ r'$\left(\widehat{p}_{1} - \widehat{p}_{2}\right)$' +f'+ {t_1}' + r'$\sqrt{\dfrac{\widehat{p}_{1}\widehat{q}_{1}}{n}+\dfrac{\widehat{p}_{2}\widehat{q}_{2}}{m}}$',fontsize=15)
ax.text(-5.5 , .15, f'신뢰구간 모비율간 차에 대한 {trust}%의 합동표본비율 : \n' + r'$Z = \dfrac{\widehat{p}_1 - \widehat{p}_2}{ \sqrt{\widehat{p}\widehat{q} * (\dfrac{1}{n} + \dfrac{1}{m}}) }$',fontsize=15)
# ax.text(-5.5 , .25, f'귀무가설 : 남자(u_1)의 입원일수가 여자(u_2)의 입원일수 보다 작다.\n u_1 < u_2' , fontsize = 15)
ax.text(1 , .35, f' 신뢰구간 {trust}% 에 대한 오차 한계( ' +r'$e_{%d}) : $ '% trust + f'\n' + r'${%.3f}\sqrt{\dfrac{\widehat{p}_{1}\widehat{q}_{1}}{n}+\dfrac{\widehat{p}_{2}\widehat{q}_{2}}{m}}$ = '% t_1 + f'{round((t_1)*math.sqrt(p1*(1-p1)/n + p2*(1-p2)/m),3)} ' , fontsize= 15)
#============================================표본평균의 정규분포화 =========================================================
RATIO = round(p1 - p2,4)
SAMPLE_PROP = (627 + 651) / (952+1043)
STDS = math.sqrt( SAMPLE_PROP * (1-SAMPLE_PROP) * (1/n + 1/m))
# print(math.sqrt(SAMPLE_PROP * (1-SAMPLE_PROP) * (1/n + 1/m) ))
# print(RATIO)
# print(f'STDS :{STDS}' )
z_1 = round(RATIO/STDS , 4)
# z_1 =(9.075 - 7.114) / 1.6035
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
# z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
print(z_1)
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=t_1) , facecolor = 'red') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- scipy.stats.norm.cdf(z_1)
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
# ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
annotate_len = stats.norm.pdf(z_1, loc=0 , scale =1) /2
plt.annotate('' , xy=(z_1, annotate_len), xytext=(z_1- 1 , annotate_len) , arrowprops = dict(facecolor = 'black'))
# plt.annotate('' , xy=(-z_1, annotate_len), xytext=(1-z_1 , annotate_len) , arrowprops = dict(facecolor = 'black'))
ax.text(-1.5 , annotate_len+0.01 , f'P-VALUE: \n P(Z>={z_1}) = {round(area,4)}',fontsize=15)
b= 'N(0,1)'
plt.legend([b] , fontsize = 15 , loc='upper left')
#
# print( (9.075 - 7.114) / 1.6035)
2>p-값을 구하여 검정한다.
P-value = 0.0543
alpha = 0.05
귀무가설 : p_1 - p_2 <=0(20대의 선호도는 30대보다 낮다.) ==> 상단측검정
P-value > alpha ==> 0.0543 > 0.05 ==> 20대의 선호도가 30대보다 높다고 주장할 근거가 충분하지 않다.
EX-02) 어느 대학병원은 남자 1000명 중 56명 , 여자 1000명 중 37명이 심장 질환을 앓고 있다. 이를 기초로 하여 남녀의 심장 질환 발병 비율이 동일한지 유의수준 5%에서 검정하라.
남자의 심장 질환 발병 비율 : p1
여자의 심장 질환 발병 비율 : p2
귀무가설: p1 - p2 = 0 ==> 양측검정
대립가설 : p1 - p2 != 0
^p1 = 56/1000
^p2 = 37/1000
x = np.arange(-5,5 , .001)
fig = plt.figure(figsize=(15,8))
ax = sns.lineplot(x , stats.norm.pdf(x, loc=0 , scale =1)) #정의역 범위 , 평균 = 0 , 표준편차 =1 인 정규분포 플롯
# trust = 95 #신뢰도
ax.set_title('양측검정' ,fontsize = 18)
p1 = 56/1000
p2 = 37/1000
n = 1000
m = 1000
RATIO = round(p1 - p2,4)
print(RATIO)
SAMPLE_PROP = (56 + 37) / (1000+1000) #합동표본비율
STDS = math.sqrt( SAMPLE_PROP * (1-SAMPLE_PROP) * (1/n + 1/m))
print(STDS)
#==========================================귀무가설 기각과 채택 ====================================================
trust = 95 #신뢰도_유의수준
t_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x<=t_1) & (x>=-t_1) , facecolor = 'orange') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = 1- (1- scipy.stats.norm.cdf(t_1))
plt.annotate('' , xy=(0, .2), xytext=(2 , .2) , arrowprops = dict(facecolor = 'black'))
ax.text(2 , .2, r'$H_{0}$의 채택역' +f'\nP({-t_1}<=Z<={t_1}) : {round(area,4)}',fontsize=15)
annotate_len = stats.norm.pdf(t_1, loc=0 , scale =1) /2
ax.vlines(x= t_1, ymin= 0 , ymax= stats.norm.pdf(t_1, loc=0 , scale =1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -t_1, ymin= 0 , ymax= stats.norm.pdf(-t_1, loc=0 , scale =1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
area = round((1-area)/2,6)
ax.text(1 + t_1 , annotate_len+0.02 , r'$z_{\alpha/2} = $' + f'{t_1}\n' + r'$H_{0}$의 기각역' + f'\n'+ r'$\alpha/2 = {%.4f}$' % area,fontsize=15)
ax.text(-2.5 -t_1 , annotate_len , r'$z_{\alpha/2} = $' + f'{-t_1}\n' + r'$H_{0}$의 기각역' + f'\n'+ r'$\alpha/2 = {%.3f}$' % area,fontsize=15)
plt.annotate('' , xy=(t_1, annotate_len-0.02), xytext=(t_1+ 1 , annotate_len) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(-t_1, annotate_len-0.02), xytext=(-1-t_1 , annotate_len) , arrowprops = dict(facecolor = 'black'))
ax.text(-5.5 , .25, f'신뢰구간 모평균에 대한 {trust}% : \n' + r'$\left(\widehat{p}_{1} - \widehat{p}_{2}\right)$' +f'-{t_1}' + r'$\sqrt{\dfrac{\widehat{p}_{1}\widehat{q}_{1}}{n}+\dfrac{\widehat{p}_{2}\widehat{q}_{2}}{m}}$' +' , \n'+ r'$\left(\widehat{p}_{1} - \widehat{p}_{2}\right)$' +f'+ {t_1}' + r'$\sqrt{\dfrac{\widehat{p}_{1}\widehat{q}_{1}}{n}+\dfrac{\widehat{p}_{2}\widehat{q}_{2}}{m}}$',fontsize=15)
ax.text(-5.5 , .15, f'신뢰구간 모비율간 차에 대한 {trust}%의 합동표본비율 : \n' + r'$Z = \dfrac{\widehat{p}_1 - \widehat{p}_2}{ \sqrt{\widehat{p}\widehat{q} * (\dfrac{1}{n} + \dfrac{1}{m}}) }$',fontsize=15)
ax.text(2 , .35 , r'합동표본비율의 $ \widehat{p} = \dfrac{x + y}{n + m}$' ,fontsize= 15)
# ax.text(-5.5 , .25, f'귀무가설 : 남자(u_1)의 입원일수가 여자(u_2)의 입원일수 보다 작다.\n u_1 < u_2' , fontsize = 15)
# ax.text(1 , .35, f' 신뢰구간 {trust}% 에 대한 오차 한계( ' +r'$e_{%d}) : $ '% trust + f'\n' + r'${%.3f}\sqrt{\dfrac{\widehat{p}_{1}\widehat{q}_{1}}{n}+\dfrac{\widehat{p}_{2}\widehat{q}_{2}}{m}}$ = '% t_1 + f'{round((t_1)*math.sqrt(p1*(1-p1)/n + p2*(1-p2)/m),3)} ' , fontsize= 15)
# ax.text(-5.5 , .25, r'신뢰구간 L = $2*{%.3f}\dfrac{\sigma}{\sqrt{n}} $' % t_1 ,fontsize=15)
#
# ax.text(-5.5 , .3, r'오차한계 = ${%.3f}\dfrac{\sigma}{\sqrt{n}} $' % t_1,fontsize=15)
#============================================표본평균의 정규분포화 =========================================================
z_1 = round(RATIO/STDS , 4)
print(z_1)
# # z_2 = round((34.5 - 35) / math.sqrt(5.5**2 / 25) , 2)
# z_1 = round(scipy.stats.norm.ppf(1 - (1-(trust/100))/2) ,3 )
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=z_1) | (x<=-z_1) , facecolor = 'skyblue') # x값 , y값 , 0 , x<=0 인곳 , 색깔
ax.fill_between(x, stats.norm.pdf(x, loc=0 , scale =1) , 0 , where = (x>=t_1) | (x<=-t_1) , facecolor = 'red') # x값 , y값 , 0 , x<=0 인곳 , 색깔
area = scipy.stats.norm.cdf(-z_1) + 1 - (scipy.stats.norm.cdf(z_1))
ax.vlines(x= z_1, ymin= 0 , ymax= stats.norm.pdf(z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= -z_1, ymin= 0 , ymax= stats.norm.pdf(-z_1, loc=0 , scale =1) , color = 'black' , linestyle ='solid' , label ='{}'.format(2))
annotate_len = stats.norm.pdf(z_1, loc=0 , scale =1) /2
plt.annotate('' , xy=(z_1, annotate_len), xytext=(-z_1/2 , annotate_len) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(-z_1, annotate_len), xytext=(z_1/2 , annotate_len) , arrowprops = dict(facecolor = 'black'))
ax.text(-1.5 , annotate_len+0.01 , f'P-value : \nP(Z<={-z_1}) + P(Z>={z_1}) \n = {round(area,4)}',fontsize=15)
# ax.text(0 , annotate_len+0.01 ,f'P(Z>={-z_1})',fontsize=15)
b= 'N(0,1)'
plt.legend([b] , fontsize = 15 , loc='upper left')
p-value : 0.0436
alpha = 0.05
p-value < alpha ==> 0.0436 < 0.05 ==> 귀무가설(남자의 심장발병 비율이 동일하다.) 는 기각
'기초통계 > 대표본 가설검정' 카테고리의 다른 글
| ★모평균의 가설 검정★기초통계학-[연습문제 02 -10] (1) | 2023.01.16 |
|---|---|
| ★=이 있는것이 귀무가설★모평균의 양측검정★모평균 <= |X 상단측 검정★모평균 >= |X 하단측검정★기초통계학-[연습문제 01 -09] (2) | 2023.01.16 |
| ★귀무가설 p<=0 하단측검정★귀무가설 p>=0 ==> 하단측검정★모비율의 검정★기초통계학-[통계적 가설검정 -07] (1) | 2023.01.15 |
| ★p-value값★검정통계량의 관찰값★모평균 차의 검정★기초통계학-[통계적 가설검정 -06] (0) | 2023.01.15 |
| ★p-value값★검정통계량의 관찰값★모평균에 대한 상단측 검정★기초통계학-[통계적 가설검정 -05] (0) | 2023.01.13 |