★표본분포★이산균등분포★표본추출 방법★모집단 분포★기초통계학-[모집단 분포와 표본분포 -01]
1) 모집단 분포
1. 모집단 분포(Population Distribution)
==> 실제 현장에서 모집단의 모든 자료값을 구하는 것은 어렵다.
==> 표본을 선정하여 모집단의 특성을 과학적으로 추론 ==> 추측 통계학
==> 어떤 통계적 실험 결과인 모집단의 자료가 가지는 확률분포
2) 표본추출 방법
1. 표본추출 방법_ 단순임의 추출법(Simple Random Sampling)
==> 추측통계학은 표본을 기초로 하여 알려지지 않은 모수를 추론
==> 공정하고 객관적인 방법으로 표본을 선정해야만 함.
단순임의 추출법 ==> 모집단을 형성하고 있는 대상들의 선정 가능성이 동등하도록 추출
==>but. 시간이 부족한 환경에서는 부적당하다.
EX) 1000명의 평균 점수를 추론하기 위해 30명으로 구성된 표본을 선정 ==> 동일한 크기의 메모지에 각자의 학번 기재이후 30 장의 메모지를 꺼낸다.
2. 표본추출 방법_ 계통 추출법(Systematic Sampling)
==> 각 모집단의 각 대상에 일련번호 부여하고, 1,2,3,....n 중에서 어느 하나를 무작위로 선정한 이후로 k씩 커지는 순서로 표본 선정
EX) 1000개의 지점별로 판매한 평균 수입 추정 ==> 100개의 지점 선정
==> 100개의 매출 장부 선정하는 과정의 시간 낭비 발생
==> 0~9사이의 임의의 수를 선정 이후 10씩 커지는 숫자 선정 ==> K씩 커지도록 표본 선정
3. 표본추출 방법_ 층화 추출법(Stratified Sampling)
==> 모집단의 특성에 따라 층화된 곳에서 각 층마다 표본을 무작위로 추출
EX) 정당의 지지율에 대한 표본 추출 ==> 전국을 각 권역별로 할당된 수만큼 표본 선정
4. 표본추출 방법_ 집락 추출법(Cluster Sampling)
==> 모집단을 몇 개의 조사 단위인 집락으로 구분, 집락을 추출단위로 표본 추출
EX) 서울시 거주 가구의 월평균 소득 조사
==> 25개의 행정구역(집락)으로 분할 ==> 5개 구를 무작위로 선정하여 표본 추출
3) 표본분포
1. 표본의 크기(Sample Size) , 표본평균(Sample mean) , 표본분산(Sample Variance)
==> 모집단으로부터 표본 추출 ==> 표본으로 선정된 대상의 수
==> 선정된 표본의 평균과 분산 ==> 표본평균 , 표본분산
2. 표본분포(Sampling Distribution)
==> 모집단에서 크기 n인 표본을 반복하여 선정할 때 얻어지는 통계량의 확률분포
https://knowallworld.tistory.com/214
★DDOF = 1★모/표본분산 , 모/표본표준편차★평균편차★기초통계학-[Chapter03 - 04]
산포의 척도 ==> 평균깊이가 1.2M인 강을 키가 1.7M인 사람이 걸어서 무사히 건널 수 있는지에 대해 생각 ==> 강의 평균 깊이가 1.2M 라는 뜻은 1.2M보다 작은 부분도 있지만 1.2M보다 깊은 곳도 있을 수
knowallworld.tistory.com
==> 참고
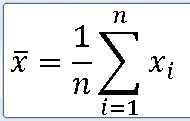
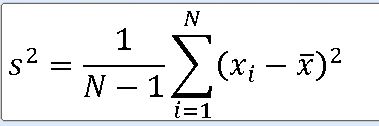
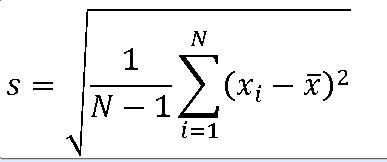
EX-01) 1,2,3,4 의 번호가 적힌 공을 주머니에 넣고 복원추출에 의해 임의로 2개를 추출하여 표본 선정==> 각각의 공이 나올 확률을 동일하게 1/4
1> 표본으로 나올 수 있는 모든 경우의 수
print(list(itertools.permutations(np.arange(1,5) , 2)))[(1, 2), (1, 3), (1, 4), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (3, 4), (4, 1), (4, 2), (4, 3)] ==>12
==> 순열
print(list(itertools.product(np.arange(1,5) , repeat = 2)))[(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4), (3, 1), (3, 2), (3, 3), (3, 4), (4, 1), (4, 2), (4, 3), (4, 4)]==>16
==> 중복순열
==> 복원추출이므로 중복순열 해야한다!
https://knowallworld.tistory.com/230
복원, 비복원 추출★SET활용하여 차집합,여집합 가능!★기초통계학-[Chapter04 - 경우의 수-03]
1. 복원추출(Replacement) ==> 표본공간에서 표본점을 선택할 때 , 동일한 표본점이 1번이상 반복하여 추출되도록 허용 EX) 1~5까지의 숫자가 적힌 공이 들어 있는 주머니에서 차례대로 2개의 공 꺼내기
knowallworld.tistory.com
2> 표본평균
a = list(itertools.product(np.arange(1,5) , repeat = 2))
a = sorted(list(set(list(map(lambda x : np.mean(x) , a)))))
a==> list(map(lambda) 활용
[1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0]
3> 표본평균 |X의 확률 분포
a = list(itertools.product(np.arange(1,5) , repeat = 2))
b = list(map(lambda x : np.mean(x) , a))
d = deque()
for i in zip(a,b):
d.append(i)
c = sorted(list(set(list(map(lambda x : np.mean(x) , a)))))
print(b)
print(c)
print(d)b ==> 표본의 요소별 평균 : [1.0, 1.5, 2.0, 2.5, 1.5, 2.0, 2.5, 3.0, 2.0, 2.5, 3.0, 3.5, 2.5, 3.0, 3.5, 4.0]
c ==> 평균 나열 : [1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0]
d ==> zip으로 나열 deque([((1, 1), 1.0), ((1, 2), 1.5), ((1, 3), 2.0), ((1, 4), 2.5), ((2, 1), 1.5), ((2, 2), 2.0), ((2, 3), 2.5), ((2, 4), 3.0), ((3, 1), 2.0), ((3, 2), 2.5), ((3, 3), 3.0), ((3, 4), 3.5), ((4, 1), 2.5), ((4, 2), 3.0), ((4, 3), 3.5), ((4, 4), 4.0)])
d = deque(sorted(d , key = lambda x : x[1]))
d
print(d)==> 요소별 평균의 순서로 sort
deque([((1, 1), 1.0), ((1, 2), 1.5), ((2, 1), 1.5), ((1, 3), 2.0), ((2, 2), 2.0), ((3, 1), 2.0), ((1, 4), 2.5), ((2, 3), 2.5), ((3, 2), 2.5), ((4, 1), 2.5), ((2, 4), 3.0), ((3, 3), 3.0), ((4, 2), 3.0), ((3, 4), 3.5), ((4, 3), 3.5), ((4, 4), 4.0)])
e =[[] for i in range(len(c))]
# print(type(d))
# print(len(a))
p=0
print(len(d))
while len(d)>=2:
if d[0][1] == d[1][1]:
e[p].append(d[0][0])
print(f'e: {e}')
d.popleft()
print(f'd: {d}')
else:
e[p].append(d[0][0])
print(f'일치 x e: {e}')
d.popleft()
p+=1
e[p].append(d[-1][0])
e==> 알고리즘 이상하다.
e ==> 2중 리스트 생성
d ==> deque이므로 popleft() 사용 가능
e = [[(1, 1)], [(1, 2), (2, 1)], [(1, 3), (2, 2), (3, 1)], [(1, 4), (2, 3), (3, 2), (4, 1)], [(2, 4), (3, 3), (4, 2)], [(3, 4), (4, 3)], [(4, 4)]]
B = pd.DataFrame([e ,c]).T
B.rename(columns= {0 : '표본' , 1: '|X'} , inplace = True)
B
b_len = [len(i) for i in B['표본']]
b_len
B['표본길이'] = b_len
B['P(|X = x)'] = B['표본길이'] / len(a)
B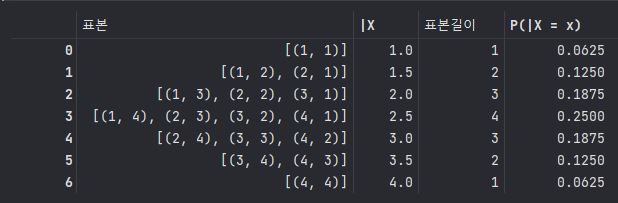
4> 표본평균 |X의 평균과 분산
B['평균'] = B['|X'] * B['P(|X = x)']
B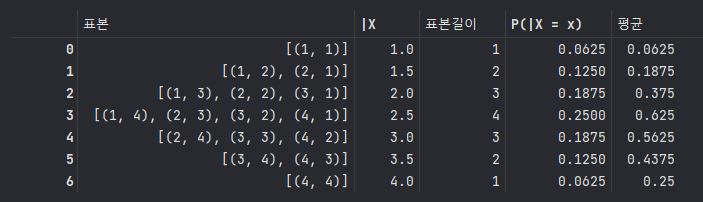
MEANS = np.sum(B['평균'])
MEANS==> 2.5
B['분산'] = (B['|X']**2) * B['P(|X = x)']
B
VARS = np.sum(B['분산'])
VARSVARS = 6.875
print(VARS - math.pow(MEANS, 2))==> 6.875 - (2.5)**2 = 0.625
print(f'모분산 var : {np.var(b ,ddof =0)}')
print(f'표본분산 var : {np.var(b ,ddof =1)}')모분산 var : 0.628
표본분산 var : 0.666666==> 틀리다?!
5> 모평균의 평균과 분산
https://knowallworld.tistory.com/245
★초기하분포★기하분포★이산균등분포★기초통계학-[Chapter05 - 이산확률분포-06]
1. 이산균등분포(Discrete Uniform Distribution) 1> 동전을 한 번 던져서 앞면이 나온 횟수를 X ==> p(x) = 1/2 , x= 0 ,1 2> 주사위를 한 번 던질 때 나온 눈의 수를 확률 변수 X라 하면 ==> p(x) = 1/6 , x =1 , 2, 3, 4, 5,
knowallworld.tistory.com
x = 1 , 2, 3, 4
평균 = (1+4)/2 = 2.5
분산 = (4**2 -1) /12 = 1.25 ==> 이산균등분포에선 np.var() 사용하면 안된다 ==> 표본분산이 아닌 모분산
==> because 다 뽑았기 때문이다!!!!!!
EX-02) 1, 2, 3 의 번호가 적힌 공을 주머니에 넣고 복원추출에 의해 임의로 2개를 추출하여 표본, 각각의 공이 나올 확률은 1/3 이다.
1> 표본으로 나올 수 있는 모든 경우의 수
a = list(itertools.product(np.arange(1,4) , repeat = 2))
print(a)
[(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)]
2> 표본의 평균
a = list(itertools.product(np.arange(1,5) , repeat = 2))
b = list(map(lambda x : np.mean(x) , a))
d = deque()
for i in zip(a,b):
d.append(i)
c = sorted(list(set(list(map(lambda x : np.mean(x) , a)))))
print(b)
print(c)
print(d)b = [1.0, 1.5, 2.0, 1.5, 2.0, 2.5, 2.0, 2.5, 3.0]
c = [1.0, 1.5, 2.0, 2.5, 3.0]
3> 표본평균 |X의 확률분포를 구하라.
d = deque(sorted(d , key = lambda x : x[1]))
e =[[] for i in range(len(c))]
# print(type(d))
# print(len(a))
p=0
print(len(d))
while len(d)>=2:
if d[0][1] == d[1][1]:
e[p].append(d[0][0])
print(f'e: {e}')
d.popleft()
print(f'd: {d}')
else:
e[p].append(d[0][0])
print(f'일치 x e: {e}')
d.popleft()
p+=1
e[p].append(d[-1][0])
e[[(1, 1)], [(1, 2), (2, 1)], [(1, 3), (2, 2), (3, 1)], [(2, 3), (3, 2)], [(3, 3)]]
B = pd.DataFrame([e ,c]).T
B.rename(columns= {0 : '표본' , 1: '|X'} , inplace = True)
B
b_len = [len(i) for i in B['표본']]
b_len
B['표본길이'] = b_len
B['P(|X = x)'] = B['표본길이'] / len(a)
B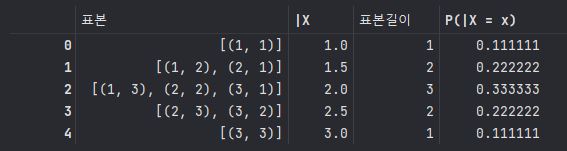
4> 표본평균 |X의 평균과 분산을 구하라.
B['평균'] = B['|X'] * B['P(|X = x)']
BMEANS = np.sum(B['평균'])
MEANS==> 2.0
B['분산'] = (B['|X']**2) * B['P(|X = x)']
B==> 0.333
b==> [1.0, 1.5, 2.0, 1.5, 2.0, 2.5, 2.0, 2.5, 3.0]
print(f'모분산 var : {np.var(b ,ddof =1)}')
print(f'표본분산 var : {np.var(b ,ddof =0)}')모분산 var : 0.375
표본분산 var : 0.3333333333333333
5> 모집단의 평균과 분산을 구하라.
모평균 = 1+3 /2 = 2
모분산 = 3**2 - 1 / 12 = 8/12 = 2/3
출처 : [쉽게 배우는 생활속의 통계학] [북스힐 , 이재원]
※혼자 공부 정리용
'기초통계 > 표본분포' 카테고리의 다른 글
| ★표본분산 S**2 , 관찰 표본분산 s_0**2★카이제곱분포표★모분산의 표본분포★기초통계학-[모집단 분포와 표본분포 -06] (0) | 2023.01.06 |
|---|---|
| ★중심극한정리★기초통계학-[모집단 분포와 표본분포 -05] (0) | 2023.01.06 |
| ★lineplot★중심극한정리★기초통계학-[모집단 분포와 표본분포 -04] (0) | 2023.01.05 |
| ★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본★표본비율★기초통계학-[모집단 분포와 표본분포 -03] (0) | 2023.01.05 |
| ★모비율★표본비율★기초통계학-[모집단 분포와 표본분포 -02] (0) | 2023.01.05 |