★하단측 , 상단측 구분할땐 변수의 순서 주목★f-분포의 양측 p-value값은 없나?★표본분산의 비에 따른 모분산 가설검정★F-분포★기초통계학-[연습문제 07- 16]
24. 서울 지역 1인당 평균소득의 분산이 울산 지역보다 큰지 알아보기 위하여, 두 지역에서 16명씩 임의로 선정하여 조사한 결과 다음표와 같았다.
A = pd.DataFrame({'평균' : [ 1854 , 1684] , '표준편차' : [69.9 , 73.3]})
A.index = ['울산' ,'서울']
A
1> 서울 지역의 분산이 울산 지역보다 큰지 유의수준 10%에서 조사하라. with p-value 값
H_0 : 서울 분산 <= 울산 분산 (상단측 검정)
X = np.arange(0,10, .01)
fig = plt.figure(figsize=(20,12))
# A = '72 75 75 80 100 110 125 150 160 200'
# B = '50 60 72 90 100 125 125 130 132 170'
#
# A = list(map(int , A.split()))
# B = list(map(int ,B.split()))
# Vars = np.var(A , ddof=1)
# Vars = 0.2**2
n = 16
m = 16
dof = [[n-1 , m-1]] #자유도
trust = 90
trust = round((1- trust/100),3)
sample_x = 1854
stand_x = 69.9
print(f'|x : {sample_x}')
print(f's_x : {stand_x}')
sample_y = 1684
stand_y = 73.3
print(f'|y : {sample_y}')
print(f's_y : {stand_y}')
#
# STDS = math.sqrt(Vars)
# MO_std = 0.3
for i in dof:
ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
X_r = scipy.stats.f(dof[0][0], dof[0][1]).ppf(1-trust)
# X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(trust)
# t_r = round( (x_0 - (0)) / (math.sqrt(33.463) * math.sqrt(1/16 + 1/16)), 3)
print(X_r)
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X<=X_r) , facecolor = 'orange')
ax.vlines(x = X_r ,ymin=0 , ymax= scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r) , colors = 'black')
# ax.vlines(x = X_l ,ymin=0 , ymax= scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l) , colors = 'black')
plt.annotate('' , xy=(X_r , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r)/2), xytext=(X_r+2 ,.1) , arrowprops = dict(facecolor = 'black'))
# plt.annotate('' , xy=(X_l , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2), xytext=(X_l + .5 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2) , arrowprops = dict(facecolor = 'black'))
area = round(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_r) ,4)
ax.text(X_r+1.5 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r) + .008 , r'$P(F\geq f_{%.3f,%2d,%2d})$' % (trust,dof[0][0] , dof[0][1]) + f'= {area}' , fontsize = 14)
# ax.text(X_l + .8 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2 , r'$P(F\leqq f_{%.3f,%2d,%2d})$' % (1-trust,dof[0][0] , dof[0][1]) + f'= {area}' , fontsize = 14)
# ax.text(X_l + 0.2 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/6 , r'$P(f_{%.3f,%2d,%2d})$' % (1-trust,dof[0][0] , dof[0][1]) + f'= {round(X_l , 2)}' , fontsize = 14)
ax.text(X_r - 1.5, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r)/6, r'$P(f_{%.3f,%2d,%2d})$' % (trust,dof[0][0] , dof[0][1]) + f'= {round(X_r , 2)}' , fontsize = 14)
ax.text(6 , 0.6 , r'$\overline{x} = {%.3f} , \overline{y} = {%.3f}$' % (sample_x, sample_y) + f'\n' + r'$s_1 = {%.3f} , s_2 = {%.3f}$' %(stand_x, stand_y), fontsize = 15)
ax.text(6 , 0.4 , f'{ (1- (trust))*100}%신뢰도 에서의 신뢰구간\n' + r'$\left(-\infty , \dfrac{s^2_1}{s^2_2}*\dfrac{1}{f_{0.95 , n-1 , m-1}}\right)$' + f'\n =' + r'$\left(-\infty , {%.3f} \right)$' % (round(stand_x**2 / stand_y**2 / X_l,4)) , fontsize = 16)
ax.text(6 , 0.2 , r'$\alpha = {%.3f}$' % ((area)) +'\n' + r'$H_0 : \sigma^2_A = \sigma^2_B$' , Fontsize = 15 )
# #=================================가설검정=====================================
ax.set_title('상단측 검정' , fontsize = 17)
X_L_1 = stand_x**2 / stand_y**2 #검정값
X_L_1 = abs(round(X_L_1,4))
if scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1) < 0.5:
X_R_1 = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1))),4)
else:
X_R_1 = X_L_1
X_L_1 = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1))),4)
print(f'X_R_1 : {X_R_1}' )
# print(f'X_L_1 : {X_L_1}' )
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X>=X_R_1) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X>=X_r) , facecolor = 'red') # x값 , y값 , 0 , X조건 인곳 , 색깔
#
area = round(float( 1 - (scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_R_1))),4)
#
# #
# ax.vlines(x= X_L_1, ymin= 0 , ymax= stats.f(dof[0][0] , dof[0][1]).pdf(X_L_1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= X_R_1, ymin= 0 , ymax= stats.f(dof[0][0] , dof[0][1]).pdf(X_R_1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
# #
annotate_len = stats.f(dof[0][0] , dof[0][1]).pdf(X_R_1) /2
# plt.annotate('' , xy=(X_L_1, annotate_len), xytext=((X_R_1+X_L_1)/2 , annotate_len) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(X_R_1, annotate_len), xytext=((X_R_1) -.5, annotate_len) , arrowprops = dict(facecolor = 'black'))
ax.text( (X_R_1)/2 , annotate_len+0.008 , f'P-value : \nP(X>={X_R_1}) \n = {area}',fontsize=15)
b = ['F({},{})'.format(i,j) for i,j in dof]
plt.legend(b , fontsize= 15)
H_0 : 서울 분산 <= 울산분산 (상단측 검정)
p-value : 0.4283
alpha : 0.1
p-value > alpha ==> 0.4283 > 0.1 ==> 귀무가설 H_0 : 서울 분산 <= 울산분산 (상단측 검정) 채택한다. 즉 , 유의수준 10%에서 서울의 분산은 울산의 분산보다 작다.
25. 서로 다른 실험 방법에 대한 반응의 분산이 서로 다른지 알아보기 위하여, 크기가 각각 8과 6인 표본을 조사하여 각각 표준편차 2.3과 5.4를 얻었다. 두 실험 방법에 대한 반응의 모분산이 서로 다른지 유의수준 5%에서 조사하라.
==>답지가 틀렸다
n = 8 , m = 6
s_1 = 2.3 , s_2 = 5.4
H_0 : 모분산_a = 모분산_b (양측검정)
X = np.arange(0,10, .01)
fig = plt.figure(figsize=(20,12))
# A = '0.8 1.8 1.0 0.1 0.9 1.7 1.4 1.0 0.9 1.2 0.5'
# B = '1.0 0.8 1.6 2.6 1.3 1.1 2.4 1.8 2.5 1.4 1.9 2.0 1.2'
#
# A= list(map(float , A.split(' ')))
# B = list(map(float , B.split(' ')))
# Vars = np.var(A , ddof=1)
# Vars = 0.2**2
n = 8
m = 6
dof = [[n-1 , m-1]] #자유도
trust = 95
trust = round((1- trust/100)/2,3)
# sample_x = np.mean(A)
stand_x = 2.3
# print(f'|x : {sample_x}')
# print(f's_x : {stand_x}')
# sample_y = np.mean(B)
stand_y = 5.4
# print(f'|y : {sample_y}')
# print(f's_y : {stand_y}')
#
# STDS = math.sqrt(Vars)
# MO_std = 0.3
for i in dof:
ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
X_r = scipy.stats.f(dof[0][0], dof[0][1]).ppf(1-trust)
X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(trust)
# t_r = round( (x_0 - (0)) / (math.sqrt(33.463) * math.sqrt(1/16 + 1/16)), 3)
print(X_r)
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X<=X_r) & (X>=X_l) , facecolor = 'orange')
ax.vlines(x = X_r ,ymin=0 , ymax= scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r) , colors = 'black')
ax.vlines(x = X_l ,ymin=0 , ymax= scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l) , colors = 'black')
plt.annotate('' , xy=(X_r , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r)/2), xytext=(X_r+2 ,.1) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(X_l , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2), xytext=(X_l + .5 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2) , arrowprops = dict(facecolor = 'black'))
area = round(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_r) ,4)
ax.text(X_r+1.5 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r) + .08 , r'$P(F\leqq f_{%.3f,%2d,%2d})$' % (trust,dof[0][0] , dof[0][1]) + f'= {area}' , fontsize = 14)
ax.text(X_l + .8 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2 , r'$P(F\leqq f_{%.3f,%2d,%2d})$' % (1-trust,dof[0][0] , dof[0][1]) + f'= {area}' , fontsize = 14)
ax.text(X_l + 0.2 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/6 , r'$P(f_{%.3f,%2d,%2d})$' % (1-trust,dof[0][0] , dof[0][1]) + f'= {round(X_l , 2)}' , fontsize = 14)
ax.text(X_r - 1.5, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r)/6, r'$P(f_{%.3f,%2d,%2d})$' % (trust,dof[0][0] , dof[0][1]) + f'= {round(X_r , 2)}' , fontsize = 14)
ax.text(6 , 0.6 , r' $s_1 = {%.3f} , s_2 = {%.3f}$' %(stand_x, stand_y), fontsize = 15)
ax.text(6 , 0.4 , f'{ (1- (trust*2))*100}%신뢰도 에서의 신뢰구간\n' + r'$\left(\dfrac{s^2_1}{s^2_2}*\dfrac{1}{f_{0.05 , n-1 , m-1}} , \dfrac{s^2_1}{s^2_2}*\dfrac{1}{f_{0.95 , n-1 , m-1}}\right)$' + f'\n =' + r'$\left( {%.3f} , {%.3f} \right)$' % (round(stand_x**2 / stand_y**2 / X_r,4) , round(stand_x**2 / stand_y**2 / X_l,4)) , fontsize = 16)
ax.text(6 , 0.2 , r'$\alpha = {%.3f}$' % ((area*2)) +'\n' + r'$H_0 : \sigma^2_A = \sigma^2_B$' , Fontsize = 15 )
# #=================================가설검정=====================================
#
ax.set_title('양측 검정' , fontsize = 17)
#
X_L_1 = stand_x**2 / stand_y**2 #검정값
X_L_1 = abs(round(X_L_1,4))
if scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1) < 0.5:
X_R_1 = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1))),4)
else:
X_R_1 = X_L_1
X_L_1 = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1))),4)
print(f'X_R_1 : {X_R_1}' )
print(f'X_L_1 : {X_L_1}' )
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X>=X_R_1) | (X<=X_L_1) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X>=X_r) | (X<=X_l) , facecolor = 'red') # x값 , y값 , 0 , X조건 인곳 , 색깔
#
area = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1) + 1 - (scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_R_1))),4)
#
#
ax.vlines(x= X_L_1, ymin= 0 , ymax= stats.f(dof[0][0] , dof[0][1]).pdf(X_L_1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= X_R_1, ymin= 0 , ymax= stats.f(dof[0][0] , dof[0][1]).pdf(X_R_1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
# #
annotate_len = stats.f(dof[0][0] , dof[0][1]).pdf(X_R_1) /2
plt.annotate('' , xy=(X_L_1, annotate_len), xytext=((X_R_1+X_L_1)/2 , annotate_len) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(X_R_1, annotate_len), xytext=((X_R_1) -.5, annotate_len) , arrowprops = dict(facecolor = 'black'))
ax.text( (X_R_1-X_L_1)/2 , annotate_len+0.008 , f'P-value : \nP(X<={X_L_1}) + P(X>={X_R_1}) \n = {area}',fontsize=15)
b = ['F({},{})'.format(i,j) for i,j in dof]
plt.legend(b , fontsize= 15)
H_0 : 모분산 a = 모분산 b (양측 검정)
p-value : 0.0449
alpha : 0.05
p-value < alpha ==> 0.0449 > 0.05 ==> 귀무가설 H_0 : 모분산 a = 모분산 b (양측 검정) 기각한다. 즉 , 유의수준 5%에서 두 실험의 반응의 분산이 서로 다르다.
26. 스마트폰을 생산하는 공정라인에서 일하는 남녀 근로자의 작업능률이 동일한지 알아보기 위하여 남녀 근로자를 각각 10명씩 임의로 추출하여 조사한 결과, 남자 근로자의 분산은 2.5이고, 여자 근로자의 분산은 2.0이었다. 남자와 여자가 생산한 스마트폰의 모분산에 차이가 있는지 유의수준 10%에서 조사하라.
H_0 : 남자 근로자의 모분산 = 여자 근로자의 모분산(양측 검정)
X = np.arange(0,10, .01)
fig = plt.figure(figsize=(20,12))
# A = '0.8 1.8 1.0 0.1 0.9 1.7 1.4 1.0 0.9 1.2 0.5'
# B = '1.0 0.8 1.6 2.6 1.3 1.1 2.4 1.8 2.5 1.4 1.9 2.0 1.2'
#
# A= list(map(float , A.split(' ')))
# B = list(map(float , B.split(' ')))
# Vars = np.var(A , ddof=1)
# Vars = 0.2**2
n = 10
m = 10
dof = [[n-1 , m-1]] #자유도
trust = 90
trust = round((1- trust/100)/2,3)
# sample_x = np.mean(A)
stand_x = math.sqrt(2.5)
# print(f'|x : {sample_x}')
# print(f's_x : {stand_x}')
# sample_y = np.mean(B)
stand_y = math.sqrt(2.0)
# print(f'|y : {sample_y}')
# print(f's_y : {stand_y}')
#
# STDS = math.sqrt(Vars)
# MO_std = 0.3
for i in dof:
ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
X_r = scipy.stats.f(dof[0][0], dof[0][1]).ppf(1-trust)
X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(trust)
# t_r = round( (x_0 - (0)) / (math.sqrt(33.463) * math.sqrt(1/16 + 1/16)), 3)
print(X_r)
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X<=X_r) & (X>=X_l) , facecolor = 'orange')
ax.vlines(x = X_r ,ymin=0 , ymax= scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r) , colors = 'black')
ax.vlines(x = X_l ,ymin=0 , ymax= scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l) , colors = 'black')
plt.annotate('' , xy=(X_r , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r)/2), xytext=(X_r+2 ,.1) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(X_l , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2), xytext=(X_l + .5 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2) , arrowprops = dict(facecolor = 'black'))
area = round(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_r) ,4)
ax.text(X_r+1.5 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r) + .08 , r'$P(F\leqq f_{%.3f,%2d,%2d})$' % (trust,dof[0][0] , dof[0][1]) + f'= {area}' , fontsize = 14)
ax.text(X_l + .8 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2 , r'$P(F\leqq f_{%.3f,%2d,%2d})$' % (1-trust,dof[0][0] , dof[0][1]) + f'= {area}' , fontsize = 14)
ax.text(X_l + 0.2 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/6 , r'$P(f_{%.3f,%2d,%2d})$' % (1-trust,dof[0][0] , dof[0][1]) + f'= {round(X_l , 2)}' , fontsize = 14)
ax.text(X_r - 1.5, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r)/6, r'$P(f_{%.3f,%2d,%2d})$' % (trust,dof[0][0] , dof[0][1]) + f'= {round(X_r , 2)}' , fontsize = 14)
ax.text(6 , 0.6 , r' $s_1 = {%.3f} , s_2 = {%.3f}$' %(stand_x, stand_y), fontsize = 15)
ax.text(6 , 0.4 , f'{ (1- (trust*2))*100}%신뢰도 에서의 신뢰구간\n' + r'$\left(\dfrac{s^2_1}{s^2_2}*\dfrac{1}{f_{0.05 , n-1 , m-1}} , \dfrac{s^2_1}{s^2_2}*\dfrac{1}{f_{0.95 , n-1 , m-1}}\right)$' + f'\n =' + r'$\left( {%.3f} , {%.3f} \right)$' % (round(stand_x**2 / stand_y**2 / X_r,4) , round(stand_x**2 / stand_y**2 / X_l,4)) , fontsize = 16)
ax.text(6 , 0.2 , r'$\alpha = {%.3f}$' % ((area*2)) +'\n' + r'$H_0 : \sigma^2_A = \sigma^2_B$' , Fontsize = 15 )
# #=================================가설검정=====================================
#
ax.set_title('양측 검정' , fontsize = 17)
#
X_L_1 = stand_x**2 / stand_y**2 #검정값
X_L_1 = abs(round(X_L_1,4))
if scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1) < 0.5:
X_R_1 = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1))),4)
else:
X_R_1 = X_L_1
X_L_1 = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1))),4)
print(f'X_R_1 : {X_R_1}' )
print(f'X_L_1 : {X_L_1}' )
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X>=X_R_1) | (X<=X_L_1) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X>=X_r) | (X<=X_l) , facecolor = 'red') # x값 , y값 , 0 , X조건 인곳 , 색깔
#
area = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1) + 1 - (scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_R_1))),4)
#
#
ax.vlines(x= X_L_1, ymin= 0 , ymax= stats.f(dof[0][0] , dof[0][1]).pdf(X_L_1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= X_R_1, ymin= 0 , ymax= stats.f(dof[0][0] , dof[0][1]).pdf(X_R_1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
# #
annotate_len = stats.f(dof[0][0] , dof[0][1]).pdf(X_R_1) /2
plt.annotate('' , xy=(X_L_1, annotate_len), xytext=((X_R_1+X_L_1)/2 , annotate_len) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(X_R_1, annotate_len), xytext=((X_R_1) -.5, annotate_len) , arrowprops = dict(facecolor = 'black'))
ax.text( (X_R_1-X_L_1)/2 , annotate_len+0.008 , f'P-value : \nP(X<={X_L_1}) + P(X>={X_R_1}) \n = {area}',fontsize=15)
b = ['F({},{})'.format(i,j) for i,j in dof]
plt.legend(b , fontsize= 15)
H_0 : 남자 근로자의 모분산 = 여자 근로자의 모분산(양측 검정)
p-value : 0.745
alpha : 0.1
p-value > alpha ==> 0.745 > 0.1 ==> 귀무가설 H_0 : 남자 근로자의 모분산 = 여자 근로자의 모분산(양측 검정) 채택한다. 즉 , 유의수준 10%에서 남자 근로자의 모분산과 여자 근로자의 모분산은 동일하다.
27. 서로 독립인 두 정규모집단으로부터 각각 크기 10과 16인 표본을 임의로 선정하였다. 이때 표본 1의 표준편차는 s_1 = 6.45이고 표본 2의 표준편차는 s_2 = 14.16이었다. 이자료를 근거로 H_0 : 모분산_1 = 모분산_2에 대한 대립가설을 유의수준 5%에서 조사
1> H_1 : 모분산_1 != 모분산_2
H_0 : 모분산_1 = 모분산_2 (양측검정)
X = np.arange(0,10, .01)
fig = plt.figure(figsize=(20,12))
# A = '0.8 1.8 1.0 0.1 0.9 1.7 1.4 1.0 0.9 1.2 0.5'
# B = '1.0 0.8 1.6 2.6 1.3 1.1 2.4 1.8 2.5 1.4 1.9 2.0 1.2'
#
# A= list(map(float , A.split(' ')))
# B = list(map(float , B.split(' ')))
# Vars = np.var(A , ddof=1)
# Vars = 0.2**2
n = 10
m = 16
dof = [[n-1 , m-1]] #자유도
trust = 95
trust = round((1- trust/100)/2,3)
# sample_x = np.mean(A)
stand_x = 6.45
# print(f'|x : {sample_x}')
# print(f's_x : {stand_x}')
# sample_y = np.mean(B)
stand_y = 14.16
# print(f'|y : {sample_y}')
# print(f's_y : {stand_y}')
#
# STDS = math.sqrt(Vars)
# MO_std = 0.3
for i in dof:
ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
X_r = scipy.stats.f(dof[0][0], dof[0][1]).ppf(1-trust)
X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(trust)
# t_r = round( (x_0 - (0)) / (math.sqrt(33.463) * math.sqrt(1/16 + 1/16)), 3)
print(X_r)
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X<=X_r) & (X>=X_l) , facecolor = 'orange')
ax.vlines(x = X_r ,ymin=0 , ymax= scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r) , colors = 'black')
ax.vlines(x = X_l ,ymin=0 , ymax= scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l) , colors = 'black')
plt.annotate('' , xy=(X_r , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r)/2), xytext=(X_r+2 ,.1) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(X_l , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2), xytext=(X_l + .5 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2) , arrowprops = dict(facecolor = 'black'))
area = round(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_r) ,4)
ax.text(X_r+1.5 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r) + .08 , r'$P(F\leqq f_{%.3f,%2d,%2d})$' % (trust,dof[0][0] , dof[0][1]) + f'= {area}' , fontsize = 14)
ax.text(X_l + .8 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2 , r'$P(F\leqq f_{%.3f,%2d,%2d})$' % (1-trust,dof[0][0] , dof[0][1]) + f'= {area}' , fontsize = 14)
ax.text(X_l + 0.2 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/6 , r'$P(f_{%.3f,%2d,%2d})$' % (1-trust,dof[0][0] , dof[0][1]) + f'= {round(X_l , 2)}' , fontsize = 14)
ax.text(X_r - 1.5, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r)/6, r'$P(f_{%.3f,%2d,%2d})$' % (trust,dof[0][0] , dof[0][1]) + f'= {round(X_r , 2)}' , fontsize = 14)
ax.text(6 , 0.6 , r' $s_1 = {%.3f} , s_2 = {%.3f}$' %(stand_x, stand_y), fontsize = 15)
ax.text(6 , 0.4 , f'{ (1- (trust*2))*100}%신뢰도 에서의 신뢰구간\n' + r'$\left(\dfrac{s^2_1}{s^2_2}*\dfrac{1}{f_{0.05 , n-1 , m-1}} , \dfrac{s^2_1}{s^2_2}*\dfrac{1}{f_{0.95 , n-1 , m-1}}\right)$' + f'\n =' + r'$\left( {%.3f} , {%.3f} \right)$' % (round(stand_x**2 / stand_y**2 / X_r,4) , round(stand_x**2 / stand_y**2 / X_l,4)) , fontsize = 16)
ax.text(6 , 0.2 , r'$\alpha = {%.3f}$' % ((area*2)) +'\n' + r'$H_0 : \sigma^2_A = \sigma^2_B$' , Fontsize = 15 )
# #=================================가설검정=====================================
#
ax.set_title('양측 검정' , fontsize = 17)
#
X_L_1 = stand_x**2 / stand_y**2 #검정값
X_L_1 = abs(round(X_L_1,4))
if scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1) < 0.5:
X_R_1 = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1))),4)
else:
X_R_1 = X_L_1
X_L_1 = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1))),4)
print(f'X_R_1 : {X_R_1}' )
print(f'X_L_1 : {X_L_1}' )
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X>=X_R_1) | (X<=X_L_1) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X>=X_r) | (X<=X_l) , facecolor = 'red') # x값 , y값 , 0 , X조건 인곳 , 색깔
#
area = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1) + 1 - (scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_R_1))),4)
#
#
ax.vlines(x= X_L_1, ymin= 0 , ymax= stats.f(dof[0][0] , dof[0][1]).pdf(X_L_1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= X_R_1, ymin= 0 , ymax= stats.f(dof[0][0] , dof[0][1]).pdf(X_R_1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
# #
annotate_len = stats.f(dof[0][0] , dof[0][1]).pdf(X_R_1) /2
plt.annotate('' , xy=(X_L_1, annotate_len), xytext=((X_R_1+X_L_1)/2 , annotate_len) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(X_R_1, annotate_len), xytext=((X_R_1) -.5, annotate_len) , arrowprops = dict(facecolor = 'black'))
ax.text( (X_R_1-X_L_1)/2 , annotate_len+0.008 , f'P-value : \nP(X<={X_L_1}) + P(X>={X_R_1}) \n = {area}',fontsize=15)
b = ['F({},{})'.format(i,j) for i,j in dof]
plt.legend(b , fontsize= 15)
H_0 : 모분산_1 = 모분산_2 (양측검정)
p-value : 0.0221
alpha : 0.05
p-value < alpha ==> 0.0221 < 0.05 ==> 귀무가설 H_0 : 모분산_1 = 모분산_2 (양측검정) 기각한다. 즉 , 유의수준 5%에서대립가설 모분산_1 != 모분산_2를 채택하다.
2> H_1 : 모분산_1 < 모분산_2
H_0 : 모분산_2 <= 모분산_1 (상단측 검정)
X = np.arange(0,10, .01)
fig = plt.figure(figsize=(20,12))
# A = '72 75 75 80 100 110 125 150 160 200'
# B = '50 60 72 90 100 125 125 130 132 170'
#
# A = list(map(int , A.split()))
# B = list(map(int ,B.split()))
# Vars = np.var(A , ddof=1)
# Vars = 0.2**2
n = 16
m = 10
dof = [[n-1 , m-1]] #자유도
trust = 95
trust = round((1- trust/100),3)
#
# sample_x = 1854
stand_x = 14.16
# print(f'|x : {sample_x}')
# print(f's_x : {stand_x}')
# sample_y = 1684
stand_y = 6.45
# print(f'|y : {sample_y}')
# print(f's_y : {stand_y}')
#
# STDS = math.sqrt(Vars)
# MO_std = 0.3
for i in dof:
ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
X_r = scipy.stats.f(dof[0][0], dof[0][1]).ppf(1-trust)
# X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(trust)
# t_r = round( (x_0 - (0)) / (math.sqrt(33.463) * math.sqrt(1/16 + 1/16)), 3)
print(X_r)
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X<=X_r) , facecolor = 'orange')
ax.vlines(x = X_r ,ymin=0 , ymax= scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r) , colors = 'black')
# ax.vlines(x = X_l ,ymin=0 , ymax= scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l) , colors = 'black')
plt.annotate('' , xy=(X_r , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r)/2), xytext=(X_r+2 ,.1) , arrowprops = dict(facecolor = 'black'))
# plt.annotate('' , xy=(X_l , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2), xytext=(X_l + .5 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2) , arrowprops = dict(facecolor = 'black'))
area = round(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_r) ,4)
ax.text(X_r+1.5 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r) + .008 , r'$P(F\geq f_{%.3f,%2d,%2d})$' % (trust,dof[0][0] , dof[0][1]) + f'= {area}' , fontsize = 14)
# ax.text(X_l + .8 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2 , r'$P(F\leqq f_{%.3f,%2d,%2d})$' % (1-trust,dof[0][0] , dof[0][1]) + f'= {area}' , fontsize = 14)
# ax.text(X_l + 0.2 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/6 , r'$P(f_{%.3f,%2d,%2d})$' % (1-trust,dof[0][0] , dof[0][1]) + f'= {round(X_l , 2)}' , fontsize = 14)
ax.text(X_r - 1.5, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r)/6, r'$P(f_{%.3f,%2d,%2d})$' % (trust,dof[0][0] , dof[0][1]) + f'= {round(X_r , 2)}' , fontsize = 14)
ax.text(6 , 0.6 , r'$\overline{x} = {%.3f} , \overline{y} = {%.3f}$' % (sample_x, sample_y) + f'\n' + r'$s_1 = {%.3f} , s_2 = {%.3f}$' %(stand_x, stand_y), fontsize = 15)
ax.text(6 , 0.4 , f'{ (1- (trust))*100}%신뢰도 에서의 신뢰구간\n' + r'$\left(-\infty , \dfrac{s^2_1}{s^2_2}*\dfrac{1}{f_{0.95 , n-1 , m-1}}\right)$' + f'\n =' + r'$\left(-\infty , {%.3f} \right)$' % (round(stand_x**2 / stand_y**2 / X_l,4)) , fontsize = 16)
ax.text(6 , 0.2 , r'$\alpha = {%.3f}$' % ((area)) +'\n' + r'$H_0 : \sigma^2_A = \sigma^2_B$' , Fontsize = 15 )
# #=================================가설검정=====================================
ax.set_title('상단측 검정' , fontsize = 17)
X_L_1 = stand_x**2 / stand_y**2 #검정값
X_L_1 = abs(round(X_L_1,4))
if scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1) < 0.5:
X_R_1 = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1))),4)
else:
X_R_1 = X_L_1
X_L_1 = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1))),4)
print(f'X_R_1 : {X_R_1}' )
# print(f'X_L_1 : {X_L_1}' )
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X>=X_R_1) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X>=X_r) , facecolor = 'red') # x값 , y값 , 0 , X조건 인곳 , 색깔
#
area = round(float( 1 - (scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_R_1))),4)
#
# #
# ax.vlines(x= X_L_1, ymin= 0 , ymax= stats.f(dof[0][0] , dof[0][1]).pdf(X_L_1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
ax.vlines(x= X_R_1, ymin= 0 , ymax= stats.f(dof[0][0] , dof[0][1]).pdf(X_R_1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
# #
annotate_len = stats.f(dof[0][0] , dof[0][1]).pdf(X_R_1) /2
# plt.annotate('' , xy=(X_L_1, annotate_len), xytext=((X_R_1+X_L_1)/2 , annotate_len) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(X_R_1, annotate_len), xytext=((X_R_1) -.5, annotate_len) , arrowprops = dict(facecolor = 'black'))
ax.text( (X_R_1)/2 , annotate_len+0.008 , f'P-value : \nP(X>={X_R_1}) \n = {area}',fontsize=15)
b = ['F({},{})'.format(i,j) for i,j in dof]
plt.legend(b , fontsize= 15)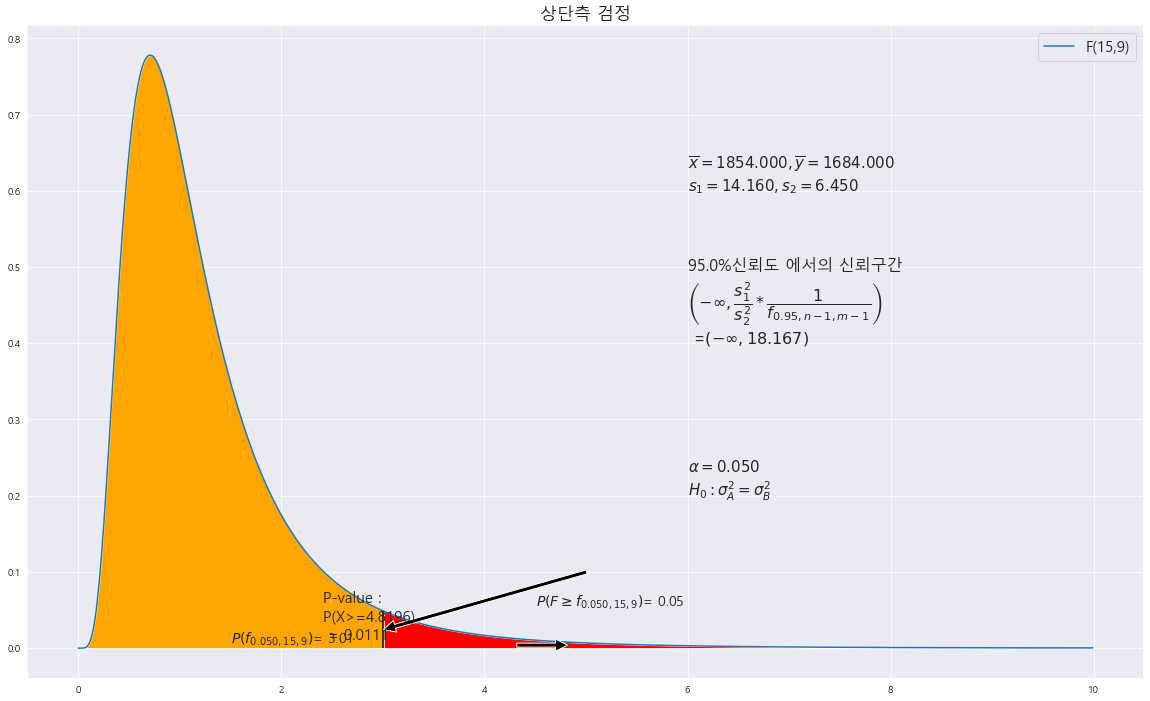
H_0 : 모분산_2 <= 모분산_1 (상단측 검정)
p-value : 0.0111
alpha : 0.05
p-value < alpha ==> 0.0111 < 0.05 ==> H_0 : 모분산_2 <= 모분산_1 (상단측 검정) 기각한다. 즉 , 유의수준 5%에서 대립가설 모분산_1 < 모분산_2 를 채택한다.
X = np.arange(0,10, .01)
fig = plt.figure(figsize=(20,12))
# A = '0.8 1.8 1.0 0.1 0.9 1.7 1.4 1.0 0.9 1.2 0.5'
# B = '1.0 0.8 1.6 2.6 1.3 1.1 2.4 1.8 2.5 1.4 1.9 2.0 1.2'
#
# A= list(map(float , A.split(' ')))
# B = list(map(float , B.split(' ')))
# Vars = np.var(A , ddof=1)
# Vars = 0.2**2
n = 10
m = 16
dof = [[n-1 , m-1]] #자유도
trust = 95
trust = round((1- trust/100),3)
# sample_x = np.mean(A)
stand_x = 6.45
# print(f'|x : {sample_x}')
# print(f's_x : {stand_x}')
# sample_y = np.mean(B)
stand_y = 14.16
# print(f'|y : {sample_y}')
# print(f's_y : {stand_y}')
#
# STDS = math.sqrt(Vars)
# MO_std = 0.3
for i in dof:
ax = sns.lineplot(X , scipy.stats.f(i[0] , i[1]).pdf(X))
# X_r = scipy.stats.f(dof[0][0], dof[0][1]).ppf(1-trust)
X_l = scipy.stats.f(dof[0][0], dof[0][1]).ppf(trust)
# t_r = round( (x_0 - (0)) / (math.sqrt(33.463) * math.sqrt(1/16 + 1/16)), 3)
# print(X_r)
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X>=X_l) , facecolor = 'orange')
#
# ax.vlines(x = X_r ,ymin=0 , ymax= scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r) , colors = 'black')
ax.vlines(x = X_l ,ymin=0 , ymax= scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l) , colors = 'black')
# plt.annotate('' , xy=(X_r , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r)/2), xytext=(X_r+2 ,.1) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(X_l , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2), xytext=(X_l + .5 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2) , arrowprops = dict(facecolor = 'black'))
area = round(scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_l) ,4)
# ax.text(X_r+1.5 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r) + .08 , r'$P(F\leqq f_{%.3f,%2d,%2d})$' % (trust,dof[0][0] , dof[0][1]) + f'= {area}' , fontsize = 14)
ax.text(X_l + .8 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/2 , r'$P(F\leqq f_{%.3f,%2d,%2d})$' % (1-trust,dof[0][0] , dof[0][1]) + f'= {area}' , fontsize = 14)
ax.text(X_l + 0.2 , scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_l)/6 , r'$P(f_{%.3f,%2d,%2d})$' % (1-trust,dof[0][0] , dof[0][1]) + f'= {round(X_l , 2)}' , fontsize = 14)
# ax.text(X_r - 1.5, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X_r)/6, r'$P(f_{%.3f,%2d,%2d})$' % (trust,dof[0][0] , dof[0][1]) + f'= {round(X_r , 2)}' , fontsize = 14)
ax.text(6 , 0.6 , r' $s_1 = {%.3f} , s_2 = {%.3f}$' %(stand_x, stand_y), fontsize = 15)
ax.text(6 , 0.4 , f'{ (1- (trust*2))*100}%신뢰도 에서의 신뢰구간\n' + r'$\left(\dfrac{s^2_1}{s^2_2}*\dfrac{1}{f_{0.05 , n-1 , m-1}} , \dfrac{s^2_1}{s^2_2}*\dfrac{1}{f_{0.95 , n-1 , m-1}}\right)$' + f'\n =' + r'$\left( {%.3f} , {%.3f} \right)$' % (round(stand_x**2 / stand_y**2 / X_r,4) , round(stand_x**2 / stand_y**2 / X_l,4)) , fontsize = 16)
ax.text(6 , 0.2 , r'$\alpha = {%.3f}$' % ((area)) +'\n' + r'$H_0 : \sigma^2_A = \sigma^2_B$' , Fontsize = 15 )
# #=================================가설검정=====================================
#
ax.set_title('하단측 검정' , fontsize = 17)
#
X_L_1 = stand_x**2 / stand_y**2 #검정값
X_L_1 = abs(round(X_L_1,4))
if scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1) < 0.5:
X_R_1 = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1))),4)
else:
X_R_1 = X_L_1
X_L_1 = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).ppf(1- scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1))),4)
print(f'X_R_1 : {X_R_1}' )
print(f'X_L_1 : {X_L_1}' )
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X<=X_L_1) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.fill_between(X, scipy.stats.f(dof[0][0] , dof[0][1]).pdf(X) , 0 , where = (X<=X_l) , facecolor = 'red') # x값 , y값 , 0 , X조건 인곳 , 색깔
#
area = round(float(scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_L_1) + 1 - (scipy.stats.f(dof[0][0] , dof[0][1]).cdf(X_R_1))),4)
#
#
ax.vlines(x= X_L_1, ymin= 0 , ymax= stats.f(dof[0][0] , dof[0][1]).pdf(X_L_1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
# ax.vlines(x= X_R_1, ymin= 0 , ymax= stats.f(dof[0][0] , dof[0][1]).pdf(X_R_1) , color = 'green' , linestyle ='solid' , label ='{}'.format(2))
# #
annotate_len = stats.f(dof[0][0] , dof[0][1]).pdf(X_R_1) /2
plt.annotate('' , xy=(X_L_1, annotate_len), xytext=((X_R_1+X_L_1)/2 , annotate_len) , arrowprops = dict(facecolor = 'black'))
# plt.annotate('' , xy=(X_R_1, annotate_len), xytext=((X_R_1) -.5, annotate_len) , arrowprops = dict(facecolor = 'black'))
ax.text( (X_L_1)+ 2 , annotate_len+0.008 , f'P-value : \nP(X<={X_L_1})) \n = {area}',fontsize=15)
b = ['F({},{})'.format(i,j) for i,j in dof]
plt.legend(b , fontsize= 15)
H_0 : 모분산_1 >= 모분산_2 (하단측 검정)
p-value : 0.0221
alpha : 0.05
p-value < alpha ==> 0.0221 < 0.05 ==> H_0 : 모분산_1 >= 모분산_2 (하단측 검정) 기각한다. 즉 , 유의수준 5%에서 대립가설 모분산_1 < 모분산_2 를 채택한다.
'기초통계 > 소표본 추론' 카테고리의 다른 글
| ★두 표본분산 , 표본의 수만 알면 F-분포 구 할 수 있다.★분산의 비에 대한 신뢰구간 구하기★F-분포★기초통계학-[연습문제 06- 15] (0) | 2023.01.19 |
|---|---|
| ★모분산 모르고 모평균 알땐 t-검정(모분산 추론)★모표준편차 추론위해서는 카이제곱분포★기초통계학-[연습문제 05- 14] (0) | 2023.01.19 |
| ★쌍체 t-검정★기초통계학-[연습문제 04- 13] (0) | 2023.01.19 |
| ★모평균의 차에 대한 가설 검정★모분산 모를땐 t-분포★줄기-잎그림★신뢰구간 구하기★기초통계학-[연습문제 03- 12] (0) | 2023.01.18 |
| ★모평균에 대한 가설 검정★모분산 모를땐 t-분포★신뢰구간 구하기★기초통계학-[연습문제 02 - 11] (0) | 2023.01.18 |