★모평균에 대한 소표본 추론★t-분포의 신뢰구간 구하기★기초통계학-[소표본 추론-01]
1. 모평균에 대한 소표본 추정
==> 대표본인 경우 , 모분산을 알고 있는 정규모집단 또는 모분산을 모르지만 대표본을 이용한 모집단의 모평균을 추론하는 방법 살펴보았다.
==> 모분산을 알고 있는 정규모집단인 경우에는 표본의 크기에 관계없이 정규분포를 사용하였다.
==> but. 대부분 모집단은 모분산이 알려져 있지 않다.
==> 모분산을 모르고 표본의 크기가 작은 경우에 모평균을 추정하거나 검정하는 통계적 추론을 살펴볼 필요가 있다.
https://knowallworld.tistory.com/302
★모분산을 모를땐 t-분포!★stats.norm.cdf()★모분산을 알때/모를때 표본평균의 표본분포★일표본
1. 표본평균의 표본분포(모분산을 아는 경우) ==> 표본평균에 대한 표본분포는 정규분포를 따른다. EX-01) 모평균 100 , 모분산 9인 정규모집단으로부터 크기 25인 표본을 임의로 추출 1> 표본평균 |X
knowallworld.tistory.com
==> 모표준편차가 알려지지 않은 경우에 표본평균 |X의 표준화에서 모표준편차를 표본표준편차 s로 대치하면, |X의 표준화 확률변수는 자유도가 n-1인 t-분포를 따른다.
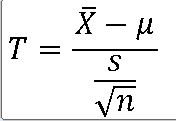
EX-01) 정규모집단에서 크기 10인 표본을 추출하여 조사
A = [3.1 , 1.9 , 2.4 , 2.8 , 2.9 , 3.0 , 2.8 , 2.3, 2.2 , 2.6]
print(f'평균 : {np.mean(A)}')
print(f'표본분산 : {np.var(A ,ddof=1)}')
print(f'표본표준편차 : {np.std(A ,ddof=1)}')평균 : 2.6
표본분산 : 0.1511111111111111
표본표준편차(s) : 0.3887
==> 모분산 모른다 ==> t-분포 활용
X = np.arange(-5,5 , .01)
fig = plt.figure(figsize=(15,8))
A = [3.1 , 1.9 , 2.4 , 2.8 , 2.9 , 3.0 , 2.8 , 2.3, 2.2 , 2.6]
MEANS = round(np.mean(A),4)
STDS = round(np.std(A , ddof=1) ,4)
n = 10 #표본개수
dof_2 = [n-1] #자유도c
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
trust = 95 #신뢰도
trust = round( (1- trust/100)/2 , 4)
t_r = scipy.stats.t(dof_2).ppf(1- trust)
print(t_r)
t_l = scipy.stats.t(dof_2).ppf(trust)
print(t_l)
E = round(float(t_r * STDS / math.sqrt(n)),4)
# =========================================================
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) | (X<=t_l) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X<t_r) & (X>t_l) , facecolor = 'orange') # x값 , y값 , 0 , X조건 인곳 , 색깔
area = round(float(scipy.stats.t(dof_2).cdf(t_r) - scipy.stats.t(dof_2).cdf(t_l)),4)
plt.annotate('' , xy=(0, .2), xytext=(-2.5 , .25) , arrowprops = dict(facecolor = 'black'))
ax.text(-4.6 , .27, f'평균(MEANS) = {MEANS}\n alpha = {round(1-area,4)}\n' + r'$t_{\dfrac{\alpha}{2}} = {%.4f}$' % t_r +f'\n n = {n} \n 표준편차(s) = {STDS}\n' +r'오차한계 $e_{95\% } = t_{\dfrac{\alpha}{2}}*\dfrac{s}{\sqrt{n}}$'+f'= {E}',fontsize=15)
plt.annotate('' , xy=(0, .25), xytext=(1.5 , .25) , arrowprops = dict(facecolor = 'black'))
ax.text(1.6 , .25, r'$P(t_{%.3f}<T<t_{%.3f})$' % (trust , 1-trust) + f'= {area}\n' + r'신뢰구간 = (MEANS -$e_{\alpha}$ , MEANS + $e_{\alpha}$)' +f'\n' + r' = $({%.4f} - {%.4f} , {%.4f} + {%.4f})$' % (MEANS, E , MEANS , E) +f'\n' +r'$ = ({%.4f} , {%.4f})$' % (MEANS-E , MEANS+E) ,fontsize=15)
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
ax.vlines(x = t_l ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_l) , colors = 'black')
plt.annotate('' , xy=(3.0, .007), xytext=(2.5 , .1) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(-3.0, .007), xytext=(-3.5 , .1) , arrowprops = dict(facecolor = 'black'))
ax.text(1.71 , .13, r'$P(T>t_{%.3f})$' % trust + f'= {round(float(1- scipy.stats.t(dof_2).cdf(t_r)),3)}',fontsize=15)
ax.text(-3.71 , .13, r'$P(T<t_{%.3f})$' % trust + f'= {round(float(scipy.stats.t(dof_2).cdf(t_l)),3)}',fontsize=15)
ax.text(t_r - 1 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
ax.text(t_l + .2 , 0.02 , r'$t_l$' + f'= {t_l}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)
==> (2.3219 , 2.8781)
EX-02) 정규모집단에서 크기 17인 표본을 추출하여 조사한 결과 , 표본평균 41 , 표본표준편차 3.2였다. 이때 | |X - m | 에 대한 95% 오차한계와 모평균에 대한 95% 신뢰구간을 구하라.
X = np.arange(-5,5 , .01)
fig = plt.figure(figsize=(15,8))
MEANS = 41
STDS = 3.2
n = 17 #표본개수
dof_2 = [n-1] #자유도c
ax = sns.lineplot(x = X , y=scipy.stats.t(dof_2).pdf(X) )
trust = 95 #신뢰도
trust = round( (1- trust/100)/2 , 4)
t_r = scipy.stats.t(dof_2).ppf(1- trust)
print(t_r)
t_l = scipy.stats.t(dof_2).ppf(trust)
print(t_l)
E = round(float(t_r * STDS / math.sqrt(n)),4)
# =========================================================
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X>=t_r) | (X<=t_l) , facecolor = 'skyblue') # x값 , y값 , 0 , X조건 인곳 , 색깔
ax.fill_between(X, scipy.stats.t(dof_2).pdf(X) , 0 , where = (X<t_r) & (X>t_l) , facecolor = 'orange') # x값 , y값 , 0 , X조건 인곳 , 색깔
area = round(float(scipy.stats.t(dof_2).cdf(t_r) - scipy.stats.t(dof_2).cdf(t_l)),4)
plt.annotate('' , xy=(0, .2), xytext=(-2.5 , .25) , arrowprops = dict(facecolor = 'black'))
ax.text(-4.6 , .27, f'평균(MEANS) = {MEANS}\n alpha = {round(1-area,4)}\n' + r'$t_{\dfrac{\alpha}{2}} = {%.4f}$' % t_r +f'\n n = {n} \n 표준편차(s) = {STDS}\n' +r'오차한계 $e_{95\% } = t_{\dfrac{\alpha}{2}}*\dfrac{s}{\sqrt{n}}$'+f'= {E}',fontsize=15)
plt.annotate('' , xy=(0, .25), xytext=(1.5 , .25) , arrowprops = dict(facecolor = 'black'))
ax.text(1.6 , .25, r'$P(t_{%.3f}<T<t_{%.3f})$' % (trust , 1-trust) + f'= {area}\n' + r'신뢰구간 = (MEANS -$e_{\alpha}$ , MEANS + $e_{\alpha}$)' +f'\n' + r' = $({%.4f} - {%.4f} , {%.4f} + {%.4f})$' % (MEANS, E , MEANS , E) +f'\n' +r'$ = ({%.4f} , {%.4f})$' % (MEANS-E , MEANS+E) ,fontsize=15)
ax.vlines(x = t_r ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_r) , colors = 'black')
ax.vlines(x = t_l ,ymin=0 , ymax= scipy.stats.t(dof_2).pdf(t_l) , colors = 'black')
plt.annotate('' , xy=(3.0, .007), xytext=(2.5 , .1) , arrowprops = dict(facecolor = 'black'))
plt.annotate('' , xy=(-3.0, .007), xytext=(-3.5 , .1) , arrowprops = dict(facecolor = 'black'))
ax.text(1.71 , .13, r'$P(T>t_{%.3f})$' % trust + f'= {round(float(1- scipy.stats.t(dof_2).cdf(t_r)),3)}',fontsize=15)
ax.text(-3.71 , .13, r'$P(T<t_{%.3f})$' % trust + f'= {round(float(scipy.stats.t(dof_2).cdf(t_l)),3)}',fontsize=15)
ax.text(t_r - 1 , 0.02 , r'$t_r$' + f'= {t_r}' , fontsize = 13)
ax.text(t_l + .2 , 0.02 , r'$t_l$' + f'= {t_l}' , fontsize = 13)
b = ['t-(n={})'.format(i) for i in dof_2]
plt.legend(b , fontsize = 15)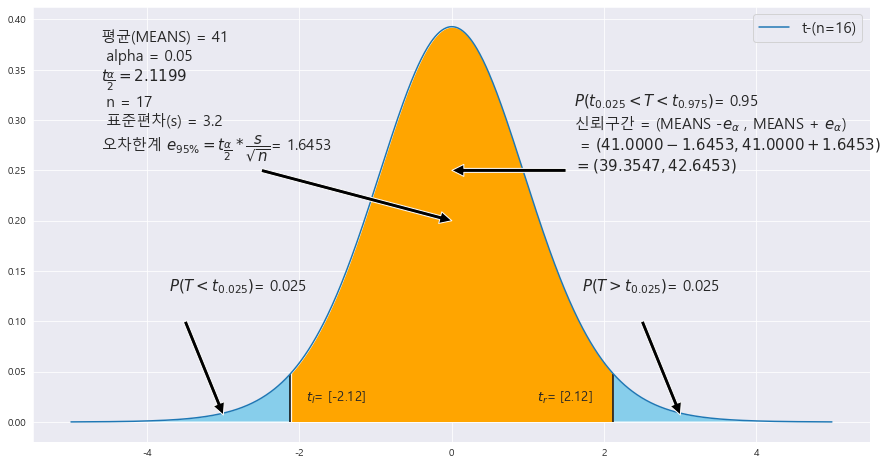
==> (39.3547 , 42.6453)
'기초통계 > 소표본 추론' 카테고리의 다른 글
| ★카이제곱분포★모분산에 대한 소표본 추론★기초통계학-[소표본 추론-06] (0) | 2023.01.18 |
|---|---|
| ★쌍체 t-검정★기초통계학-[소표본 추론-05] (0) | 2023.01.17 |
| ★모평균의 차에 대한 소표본 가설검정★기초통계학-[소표본 추론-04] (0) | 2023.01.17 |
| ★t-분포의 합동표본분산 구하는거 기억하기★모평균 차에 대한 소표본 추정★기초통계학-[소표본 추론-03] (0) | 2023.01.17 |
| t-분포는 모분산 모를때★t-분포의 모평균에 대한 검정통계량★T-분포에 대한 양측검정★상단측검정★하단측검정★기초통계학-[소표본 추론-02] (0) | 2023.01.17 |