[백준 파이썬 1193번]분수찾기 ★계수함수 & 대각선의 길이에 따른 분수의 규칙 이해하기★함수활용★VER2.0
VERSION 2.0
import sys
import math
A = int(sys.stdin.readline())
def func(k):
a = (pow(k,2) - k + 2)//2
return a
k=1
while True:
if func(k) <= A < func(k+1):
break
else:
k+=1
if k% 2 == 1:
bun_za = func(k) - A +k
bun_mo = A-func(k)+1
else:
bun_za = A -func(k) +1
bun_mo = func(k) - A + k
print( '{}/{}'.format(bun_za,bun_mo))VERSION 1.0

import sys
X = int(sys.stdin.readline())
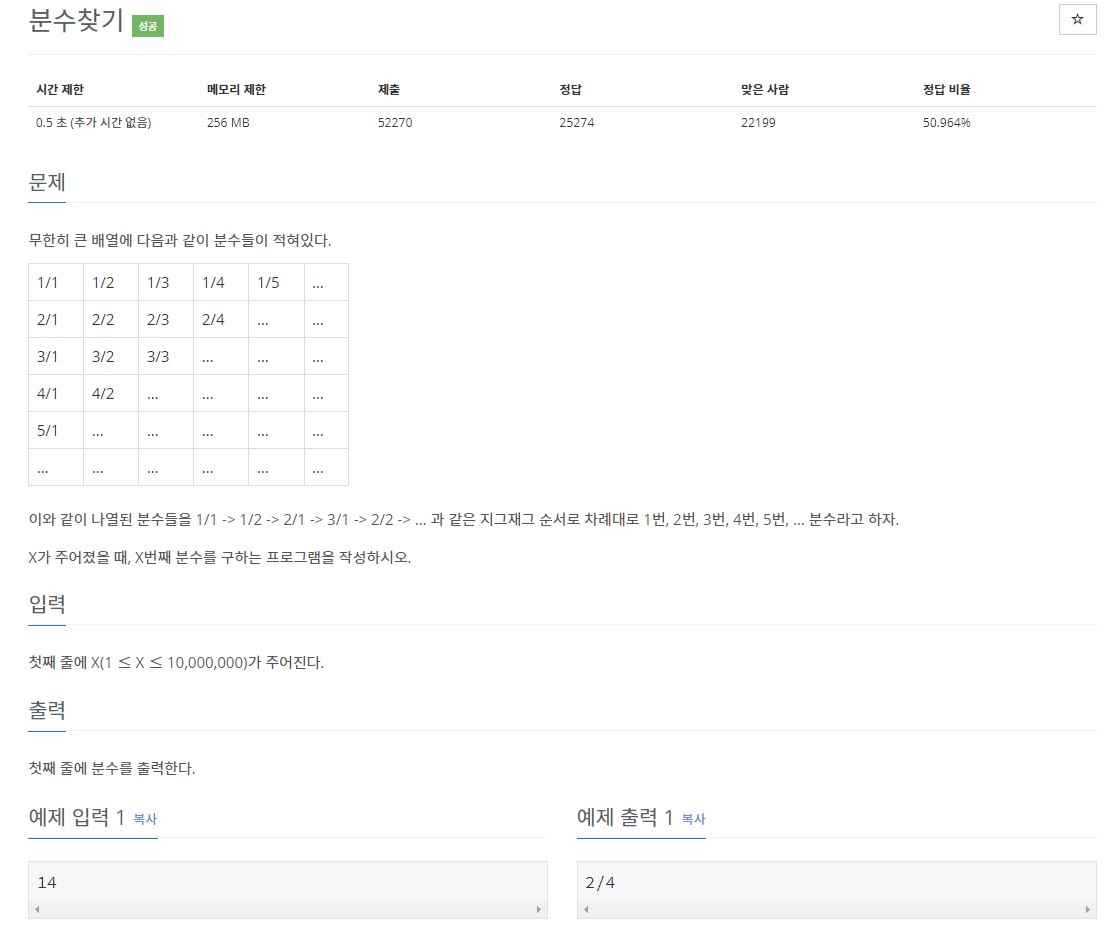
#1/1 ==> 1번째
#1/2 2/1 ==> 2 3 번째 ==>오른쪽위에서 왼쪽아래로
#3/1 2/2 1/3 ==>4 5 6 번째==>왼쪽아래에서 오른쪽 위로
#1/4 2/3 3/2 4/1 ==> 7 8 9 10번째==>오른쪽위에서 왼쪽아래로
#5/1 4/2 3/3 2/4 1/5 ==> 11 12 13 14 15번째==>왼쪽아래에서 오른쪽위로
#1/6 2/5 3/4 4/3 5/2 6/1 ==> 16 17 18 19 20 21
#i=0
# a[0]==> [i+1/i+1]
#i=1
#a[1] ==> [i/i+1] [i+1/i]
k=1
A,B =[] , []
def func(n):
range1 = int((n*(n-1)//2)+1) #계차수열 1 2 4 7
return range1
while True:
if func(k)<=X<func(k+1):
#ex> k=1 X=14 ==> func(1) = 1
#k=2 ==>func(2) =2
#k=3 ==>func(3) = 4
#k=4 ==>func(4) = 7
#k=5 ==>func(5) = 11 <= X <func(6)=16
print('인덱스{}는 {}번째 대각선 라인에 존재'.format(X,k))
#X는 5번째 대각선 라인에 존재
a,b=0,0
for i in range(func(k),func(k+1)):
#range(11,16) ==> 11~15
a+=1
if i == X: #11==14(?) a=1 X 12==14(?) a=2 X 13==14(?) a=3 X 14==14 a=4 O
print("{}번째에 존재합니다.".format(a)) #4번째에 존재합니다.
b =a
A.append(i) #[11,12,13,14]
else:#11!=14 12!=14 13!=14
A.append(i) #[11] ==> [11,12] ==>[11,12,13]
continue
break
else:
k+=1
print(A)
print(b)
if len(A)%2 == 1:
print("{}/{}".format(len(A)-b+1,b))
else:
print("{}/{}".format(b,len(A)-b+1))
★★★KEY POINT★★★
1. 인덱스의 위치 파악하는것이 중요!!
#1/1 ==> 1번째(인덱스)
#1/2 2/1 ==> 2 3 번째 ==>오른쪽위에서 왼쪽아래로
#3/1 2/2 1/3 ==>4 5 6 번째==>왼쪽아래에서 오른쪽 위로
#1/4 2/3 3/2 4/1 ==> 7 8 9 10번째==>오른쪽위에서 왼쪽아래로
#5/1 4/2 3/3 2/4 1/5 ==> 11 12 13 14 15번째==>왼쪽아래에서 오른쪽위로
#1/6 2/5 3/4 4/3 5/2 6/1 ==> 16 17 18 19 20 21
==> 여기서 알 수 있는점!!!! : 각 대각선마다 인덱스는 하나씩 늘어나는것을 알 수 있다.
대각선으로 하나의 리스트라고 생각하자!
2. 계수함수 잘 기억해두기
16번째줄~~~: func(k) 선언 : int(n*(n-1)/2 +1) 의 계차수열로서 return 값을 부여하는 함수를 정의한다.
while True:
if func(k)<=X<func(k+1):
#ex> k=1 이고, X=14 일때 ==> func(1) = 1 <= X <2 이므로 다음 ELSE문으로 넘어감(k+=1)
#k=2 ==>func(2) = 2 <= X <4 이므로 다음 ELSE문으로 넘어감(k+=1)
#k=3 ==>func(3) = 4 <= X <7 이므로 다음 ELSE문으로 넘어감(k+=1)
#k=4 ==>func(4) = 7 <= X <11 이므로 다음 ELSE문으로 넘어감(k+=1)
#k=5 ==>func(5) = 11 <= X <func(6)=16 이므로 if문 실행 하게 된다!!
print('인덱스{}는 {}번째 대각선 라인에 존재'.format(X,k))
#X는 5번째 대각선 라인에 존재
else:
k+=1
28번째 줄~~~:
위의 print문 실행되고 난뒤,
a,b=0,0
for i in range(func(k),func(k+1)):
#range(11,16) ==> 11~15
a+=1 ==> a는 대각선의 몇번째에 위치해 있는지 알려준다. 인덱스와 1씩 차이난다.
if i == X: #11==14(?) a=1 X 12==14(?) a=2 X 13==14(?) a=3 X 14==14 a=4 O
print("{}번째에 존재합니다.".format(a)) #4번째에 존재합니다.
b =a ==>b는 X의 위치가 대각선의 어디에 있는지를 저장한다.
A.append(i) #[11,12,13,14]
else:#11!=14 12!=14 13!=14
A.append(i) #[11] ==> [11,12] ==>[11,12,13]
continue
3. 분수 규칙 이해해보기
분수의 규칙:
대각선의 순서가 홀수 일때:
분모가 내가 찾은 분수가 있는 대각선의 길이에서 점차 줄어들고
분자는 1에서부터 커진다는 것을 알 수있다.
대각선의 순서가 짝수일때:
분모는 1에서부터 커지고,
분자는 내가 찾은 분수가 있는 대각선의 길이에서 점차 줄어든다
if len(A)%2 == 1: ==> X가 14일때 A의 길이는 5 5%2 == 1 A =[11,12,13,14,15]
print("{}/{}".format(len(A)-b+1,b)) ==>b = 4 , 5-4+1 ==> 2/4
else: ==> X가 16일때 A의 길이는 6 6%2 == 0 A =[16,17,18,19,20,21]
print("{}/{}".format(b,len(A)-b+1)) ==>b = 1 , 6-1+1 ==> 1/6
'Python(백준) > 기본 수학 1' 카테고리의 다른 글
| [백준 파이썬 2839번]설탕배달★if문 활용 ★VER2.0 (1) | 2022.09.16 |
|---|---|
| [백준 파이썬 10250번]ACM호텔★올림함수를 이용하여 규칙 차근차근 분석해보기★ (1) | 2022.09.16 |
| [백준 파이썬 2869번]달팽이는 올라가고 싶다 ★올림함수를 활용하고 알고리즘 차근차근 분석하기★등차수열과 범위확인★VER2.0 (0) | 2022.09.16 |
| [백준 파이썬 1712번]손익분기점★손익분기 잘 이해하기★손익못넘기는거 먼저 파악★VER2.0 (0) | 2022.09.15 |
| [백준 파이썬 2292번]벌집 ★rfind() , find()함수 활용하기★ (0) | 2021.08.04 |